初めに
今回はサラッと時系列データで使用されるモデルについて説明致します。
正直メインパートだけあってここは難しいです。私もそれなりに色々なサイトから説明を参考にさせて頂きましたが、正直まだピンと来てない事も多い。
サラッと確認して次の実装に行って勝手を試してみるのも良いかもしれません。
(正直この回は次回への助走パートです)
バックナンバー
- 日大文系卒が学ぶ時系列解析① ~概念と用語紹介~
- 日大文系卒が学ぶ時系列解析② ~自己相関関数/定常性/波形分解~
- 日大文系卒が学ぶ時系列解析③ ~モデルの紹介~
- 日大文系卒が学ぶ時系列解析④ ~SARIMAの実践~
学習
今から紹介するのはARMA(アーマ)､ARIMA(アリマ)､SARIMA(サリマ),SARIMAX(サリマックス)､という聞きなれない呪文の学習を始めます。
- 実例を提示致します。下記グラフは月ごとの
平均気温の時系列データで青が実値で赤が予測値です。様々な手段を試して予測値を算出した中で、一番良いものを提示致しました。 この手段が上記のARMA､ARIMA､SARIMAetc,です。
考えは機械学習と同じです。
①値を予測したい。
②どうやって予測しようかな線形回帰、ランダムフォレスト、LightGB等…
③予測して予測した値を確認...と。
最初に見てほしい画像
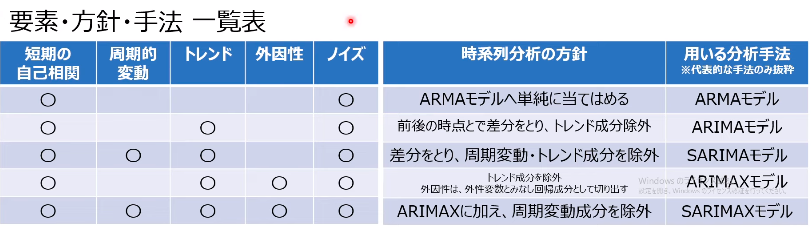
基本的に最小単位はARMAです。AR/MAモデル単発でも勿論可能ですが、とにかく実装を見てほしいので今回はスキップ致します。 参照
ARモデル(自己回帰モデル)
- 現在の値は、過去の値から決まります。つまり
現在や過去の値から未来を予測しましょうと。 - 短期の自己相関があるデータに有効(相関性のあるデータ)で、
なんでも使えるけどあまりにもシンプルすぎる。
将来のYの値は、過去のYの値によって説明できる
⇒将来の予測値は、過去の予測値により決まる
具体例：今月の売上量が多かったら、来月は売上量が増えるだろうと。
MAモデル(移動平均モデル)
- 予測する際の材料として､学習データの一つ一つを見るのではなく、tの点、tの一つ前、tの一つ後の
合計3つの点の平均から、予一つの予測点(赤)を導きましょう。という事です。
他の解釈として
- 現在の値は、過去の「実績と予測のズレ」から決まる。
「過去の値から現在を予測」というのはいくら努力してもズレ(誤差)は生じますよね。そのズレも考慮してモデルを組み立てましょうと。
この方法によりノイズがあるデータに有効です。(基本どのデータにもノイズはありますけど。)
ARMA(アーマ)モデル
-
AR+MA= ARMA 互いに競合する性質ではないので合成しても平気です。 - このARMAモデルが基本で実装する際もこれを最小単位としてどんどんパワーアップする。というやり方を行います。
ARIMA(アリマ)モデル
ARMAモデルに差分過程（階差）という概念を付け加えました。
- 原系列を階差数列に変換した後、ARMAモデルへ適応したもの。
- つまり仕組みを理解するにはlogの知識が必要。
今回は実装をしてその事も確認できればと。 - おそらくトレンドを分解除去する事が出来るので、長期トレンドがあるデータに有効。
SARIMA(サリマ)モデル
ARIMAモデルを更に季節周期を持つデータに対応できるように拡張しました。(パワーアップ)。
- 季節周期
1年間での周期変動：例：季節関係のデータや賃金の支払い額(ボーナス)毎年6月と12月に増える みたいな。
SARIMAX(サリマックス)モデル
SARIMAモデルを更にパワーアップ。Xは変数の事です。
SARIMAモデルに外的要因を考慮して予測する手法です。
毎月の平均気温の予測
- SARIMAX以外：現在や過去の気温データから未来の気温を予測する。
- SARIMAX：現在や過去の気温データに加え降水量や気圧,その他変数等から未来の気温を予測する。
終わりに
こうしてみるといかがですかね。実務やkaggle/signateで予測する際はこの中だとSARIMXのみで行っとけば良いんじゃない？とも思っちゃいますよね。
その点に関しては次回の実装を確認して頂ければ。
正直ピンとこないし分からない。なのでとりあえず実装してみましょう。
それで何か論理の補足や発見があれば逐次アップデートを行います。
参照
終わりに
参考文献