初めに。
前回の続きです。前回はこちら。
前回のあらすじ
時系列解析の概念とボキャブラリーを紹介致しました。
今回も同じです。まずはきちっとボキャブラリーを増やして理解する事。
長文読解するには英単語からみたいなイメージで進めています。
バックナンバーはこちら。
学習
事前知識
平均/期待値 分散 標準偏差
私は分散や標準偏差は社会人になってから勉強し始めました。やばいでしょ。
共分散
xの分散とyの分散の平均。
A(英語の点数)の分散 と B(数学の点数)の分散 の平均 = 英語と数学の共分散
難しい数式はひとまずスルーで。
自己共分散
共分散に時系列の概念を取り入れたもの。
自己共分散 = 共分散 + 時系列(現在や過去の概念)
例:今季の英語テストの分散(基準点) と 前期の英語テストの分散(過去)の平均 = 自己共分散
自己相関係数ACF:Autocorrelation Function
現在のデータと過去の値がどれほど似ているか、相関関係があるか。確認できるもの。
コレログラム
自己相関係数をグラフにしたもの
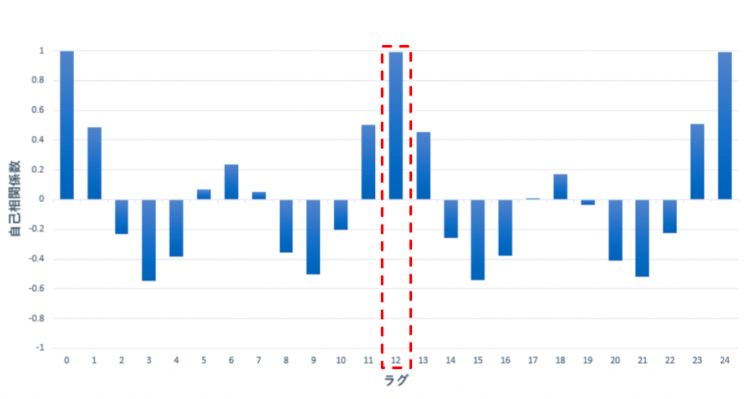
まずはコレログラムから説明させてください。下記がコレログラムです。
コレログラムの利点:周期性が分かる (伏線を張りました。今はピンと来なくて結構です。) 相関関係が分かる。
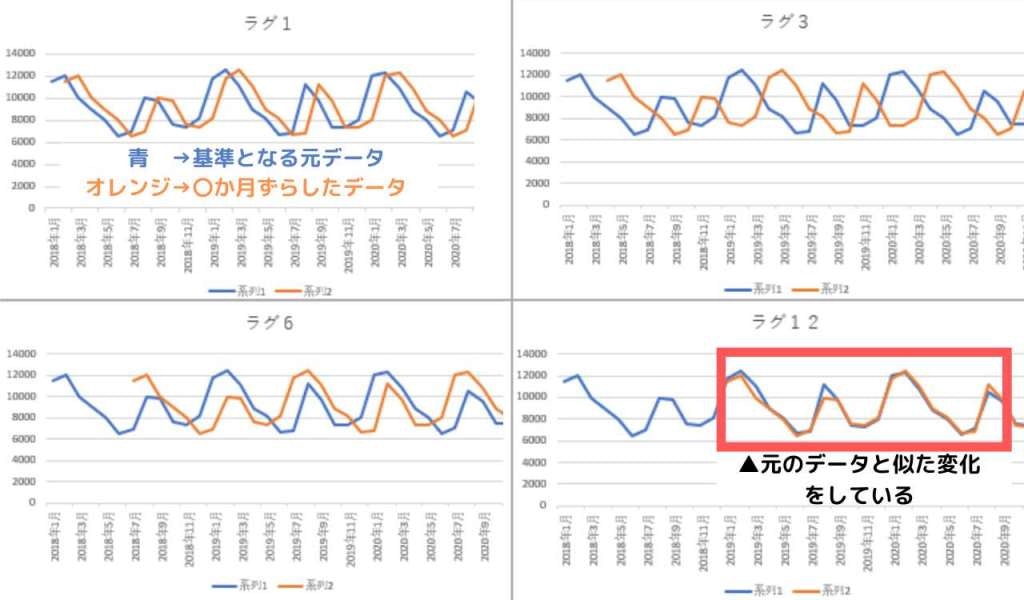
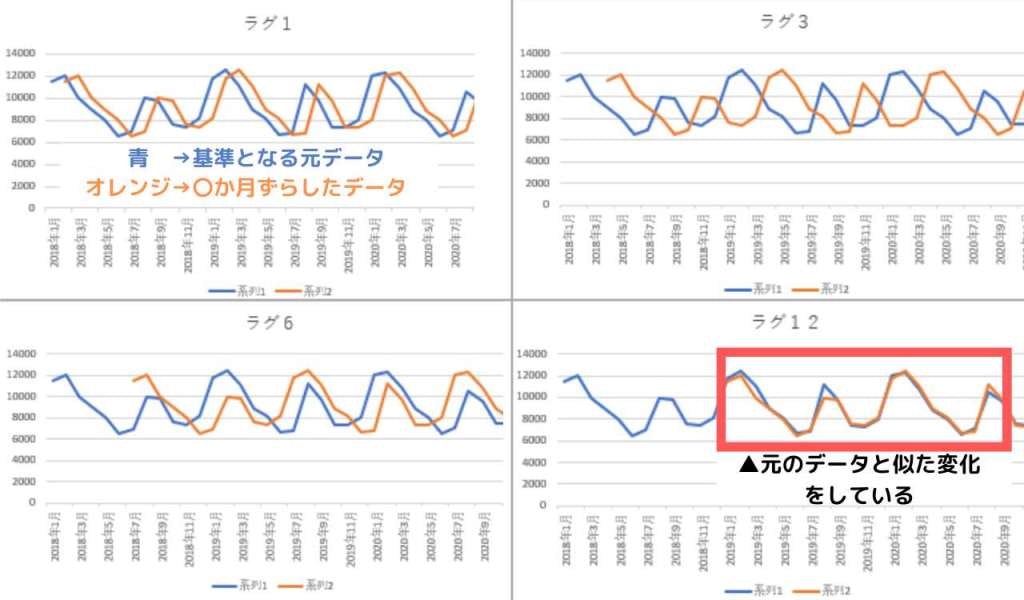
そしてこれがこのコレログラムを作成した材料の折れ線グラフです。
青とオレンジは現在のデータと過去のデータを比較しております。
青:現在のデータ。 オレンジ:過去データ。
当然現在と過去のデータを並べているので、ズレてますよね。
そのずらし具合なんですけど、できるだけズレの少ない(ラグがない)ポイントを探そう。という事です。
12がズレ(ラグ)が少ない⇒良い!という事です。
詳しくはこちら
Pythonでコレログラムを実装する
実際にpythonで確認してみましょう。
#モジュールインポート
import pandas as pd
from datetime import datetime
import seaborn as sns
import matplotlib.pyplot as plt
#データの読込。平均気温のデータです。
df = pd.read_csv("3-2_TS_sample2.csv",index_col="年月日",encoding="shift_jis",parse_dates=True)
df.head(5)
#コレログラム作成モジュール インポート
import statsmodels.api as sm
plt.rc("figure",figsize=(20,10)) #大きさの設定
# コレログラム作成
res = sm.graphics.tsa.plot_acf(df["平均気温(℃)"],lags=400)
データはこちらのサイトの「自己相関、コレログラム、波形分解」
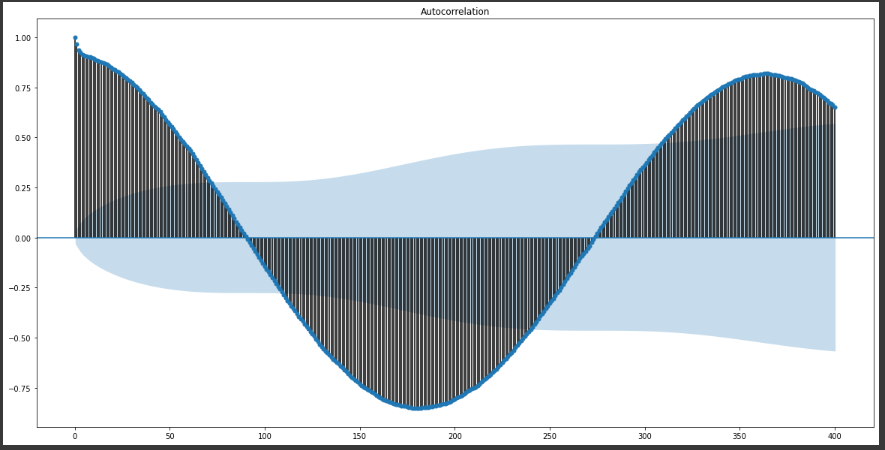
グラフの見方。
sm.graphics.tsa.plot_acf():グラフ作成
第一引数はデータ、第二引数はlags
lags:どのくらいずらすか。ちょっとずらすのか思いっきりとずらすのか。
上の折れ線グラフ「ラグ1」「ラグ2」「ラグ3」 を参照してください。
横軸:X軸をどのくらいずらしたか。lagsは400と設定しましたので、X軸の最大は400です。
縦軸:相関関係。1.00が正の相関があり、-1.00が負の相関。そして0は相関関係なし。
考察
-
例えば1や5ズラしてもあまり相関はありますよね。「昨日と今日の気温どんだけ違うの?」と言われても大差ないですよね。
しかし90~100ずらしてはいかがでしょう?3カ月だから夏と秋。さすがに温度の相関は取れませんよね。逆に半年、180くらいは夏と冬負の相関は取れています。 -
そのように考えると、
365周期なのでは? という事が見受けられるのです。
定常性
どんな時点、どんな時間差でも変わらない変化。現在や過去でも変わらない変化。
定常性が強い項目⇒時間の影響を受けない。トレンドは持たない。データ。
時間の経過によらず一定の値を軸とし、同程度の幅で振れて変化する
⇒現実世界には、こうしたデータはほとんど存在しません。
でも時系列解析の際には定常性の確認を可視化して行う事。⇒ADF検定というもので確認します。
例:500Vの電圧のデータ。⇒一定の電圧で一定の振れ幅。
定常性があるデータをそのまま時系列分析してはいけません。
⇒時系列解析の意味をなさないし、疑似相関が生じるからです。
言い換えると、定常性のあるデータに時系列という概念を組み込んではいけません。
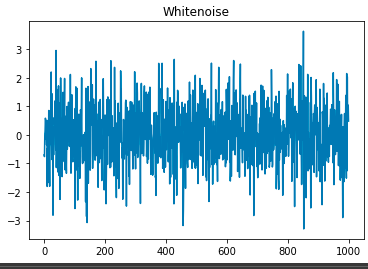
ホワイトノイズ
定常性があるデータの振れ幅の部分。
イメージはこちら。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import numpy as np
from pandas import datetime
#ホワイトノイズの設定
mean = 0
std = 1
num_samples = 1000
samples = np.random.normal(mean, std, size=num_samples)
# ホワイトノイズのプロット
plt.title("Whitenoise")
plt.plot(samples)
plt.show()
このギザギザ部分です。定常性のあるデータは時系列関係なしに一定なのですが、その一定の中でも同一の振れ幅はありますよね。その部分の事です。
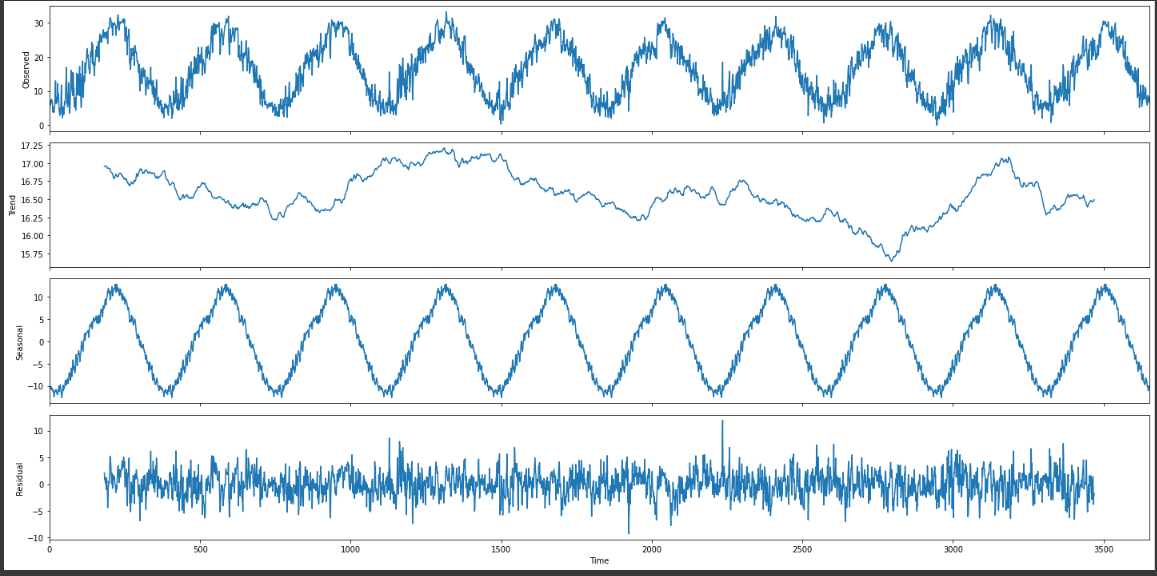
波形分解。
用語を蓄え多少レベルアップした所でグラフをお見せ致します。
データはこちらのサイトの「自己相関、コレログラム、波形分解」
import pandas as pd
from datetime import datetime
#データの読込。平均気温のデータです。
df = pd.read_csv("3-2_TS_sample2.csv",index_col="年月日",encoding="shift_jis",parse_dates=True)
#第一引数にデータを格納。 第二引数には周期を指定。今回は365。
x = sm.tsa.seasonal_decompose(df["平均気温(℃)"].values,freq=365).plot()
これは何ですか?というと、波形分解です。
その名の通り一つの原系列を分解しています。 一つのおもちゃを分解して部品ごとに確認するように。
- Observed : 元の時系列データです。
- Seasonabl: 1つの波が繰り返されています。
- Trend : 考えとしてObservedからSeasonableを抜いたデータです。
夏暑い、冬寒いという当たり前の要素を抜いた時、どうなっているかを確認する事が出来ます。
平均気温、例年と比較して低い周期がある、高い周期がある等比較できます。

- 残差(residual):細かい誤差、ノイズです。計算に入れる事が出来ず、傾向を知るうえで邪魔な外れ値みたいなものと考えております。
トレンド(Trend)+季節調整済みモデル(Seasonabl)+残差(residual)=原系列(Observed)
終わりに
だんだんとしんどくなっていきますね。正直、自己共分散についてはまだ説明や理解が足りませんよね私自身の。今結構な勢いで時系列解析の資料を読み漁っているのでこの記事も私の成長に合わせてアップデートする予定です![]() 。
。
次回は謎の暗号ARMA(アーマ)、ARIMA(アリマ)、SARIMA(サリマ)etc、について学んでいこうと思います。
参照