結論
本記事では、TDoA(Time Difference of Arrival)という位置測位技術を説明します。
実際に動かした結果ですが、簡易的な測定にもかかわらず角度-5~+8°くらいの精度で方向を算出できることを確認しました。
はじめに
昨今、スマートシティや自動運転などを筆頭に位置測位技術の重要性は高まっています。位置測位には様々な手法がありますが、どれも一長一短なので、状況に応じて適切な手法を選ぶ、あるいは複数の手法を組み合わせる工夫が求められます。
本記事では位置測位技術の一つである「音」を対象としたTDoAを紹介します。
必要機材としてマイクを2台および音響解析用のコンピュータを使うだけのため、安価な実装が可能です。
理論
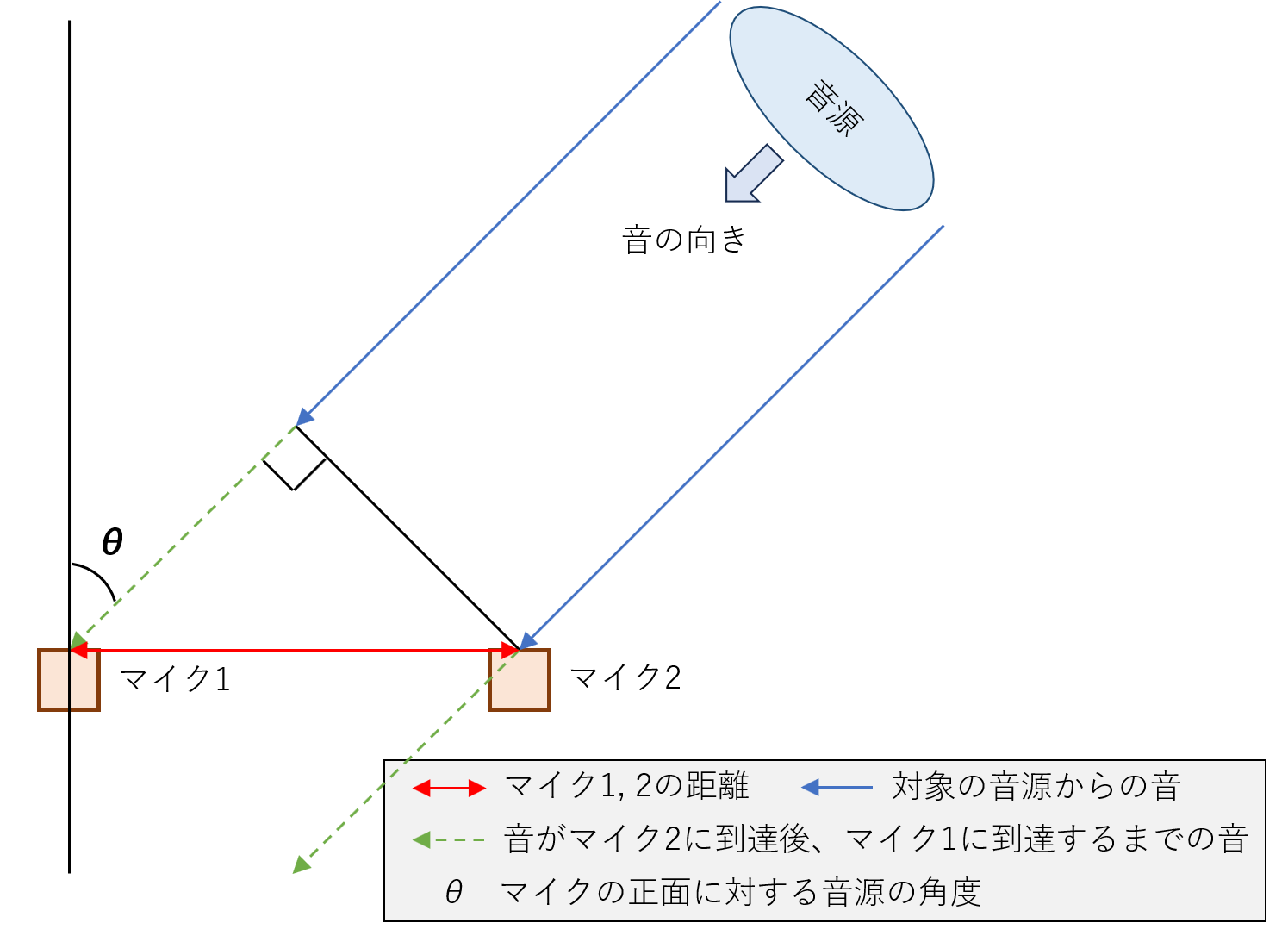
大まかに概要を知るため、以下に図を用意しました。
ある音源に対してマイク2台で音を計測し、その音の到達差によって角度を逆算し、音源の方向を特定します。
下記の式では、音が2つのマイクに到達するまでの時間差($\Delta t$)と、マイク間の距離($d$)、音速($v$)を使って、音源の方向(角度 $\theta$)を求めています。
- $\theta$:音源の角度
- $v$:音速(室温が28℃のため348 m/sとする)
- $\Delta t$:2つのマイク間の音の到達時間差
- $d$:マイク間の距離(今回は0.15mで設置した)
$$
\theta = \sin^{-1} \left( \frac{v \cdot \Delta t}{d} \right) \cdot \left( \frac{180}{\pi} \right)
$$
音速は気温によって変わるので注意してください。
ここで得られる角度 $\theta$ は、マイク間に直線を引いたとき、その中心を基準とした角度になります(正面が0度、左右に最大±90度)。
計算される角度 $\theta$ はラジアン単位で得られるため、最後に $180/\pi$ を掛けて度(°)に変換しています。
アークサイン($\sin^{-1}$)は、三角関数の逆関数で、ある比率に対応する角度を求める関数です。
数式がやや複雑なため、直感的に分かりやすいよう、以下で実際に動かしてみたいと思います。
機材
今回実験に使った機材です。
TDoAで確認したい内容は、音が各マイクに届いた時間です。
今回はありもので確認をしているため、オシロスコープで音の到達時間を確認します。しかし例えば、2入力以上のオーディオインターフェースを持っている方であればそれを使っても大丈夫です。
(上の方法は金額が高いです。技術をお持ちであれば、高性能なADCが搭載されているマイコンを使って波形を確認することで、かなり安く済むと思います。)
- マイク
秋月のコンデンサマイクです。ハンダ付けが5か所必要ですので、このマイクを用いる場合はハンダごてが必要です。
5Vを印加することで、2.5Vを基準とした±2.5Vの波形を出力してくれます。
- カスタネット
鈴木楽器のカスタネットです。今回は音源として用いますが、これに関しては音が出れば何でもいいです。
- オシロスコープ
本記事では以下のようなオシロスコープを使用しましたが、2ch対応であれば他のモデルでも問題ありません。
マイクと音源配置
以下が計測した際のマイクと音源の位置関係です。
(写真を撮るにあたり、周りを急いで片づけました。)
ブレッドボードの両端に刺してある緑色の基板がコンデンサマイクです。本記事では左側をマイク1、右側をマイク2と定義しておきます。
マイク間の中心を原点とし、90°、45°、0°、-45°の位置(分かりやすいようにピンを立てています)でカスタネットを鳴らし、その音の波形を確認します。
ただし、注意点として音源との距離を考慮する必要があります。今回は場所が狭い関係で、マイクと音源の距離が非常に近いです。本来TDoAは音源が十分に離れており、音が平面波で届く場合に成り立ちます。
今回のように距離が近いと、音が平面波として届かず計算結果にひずみが生まれます。本記事ではひずみを許容して確認を進めますが、もし何らかのシステムにTDoAを組み込む際は注意してください。
計測結果
実際にカスタネットで音を鳴らし、オシロスコープで計測しました。
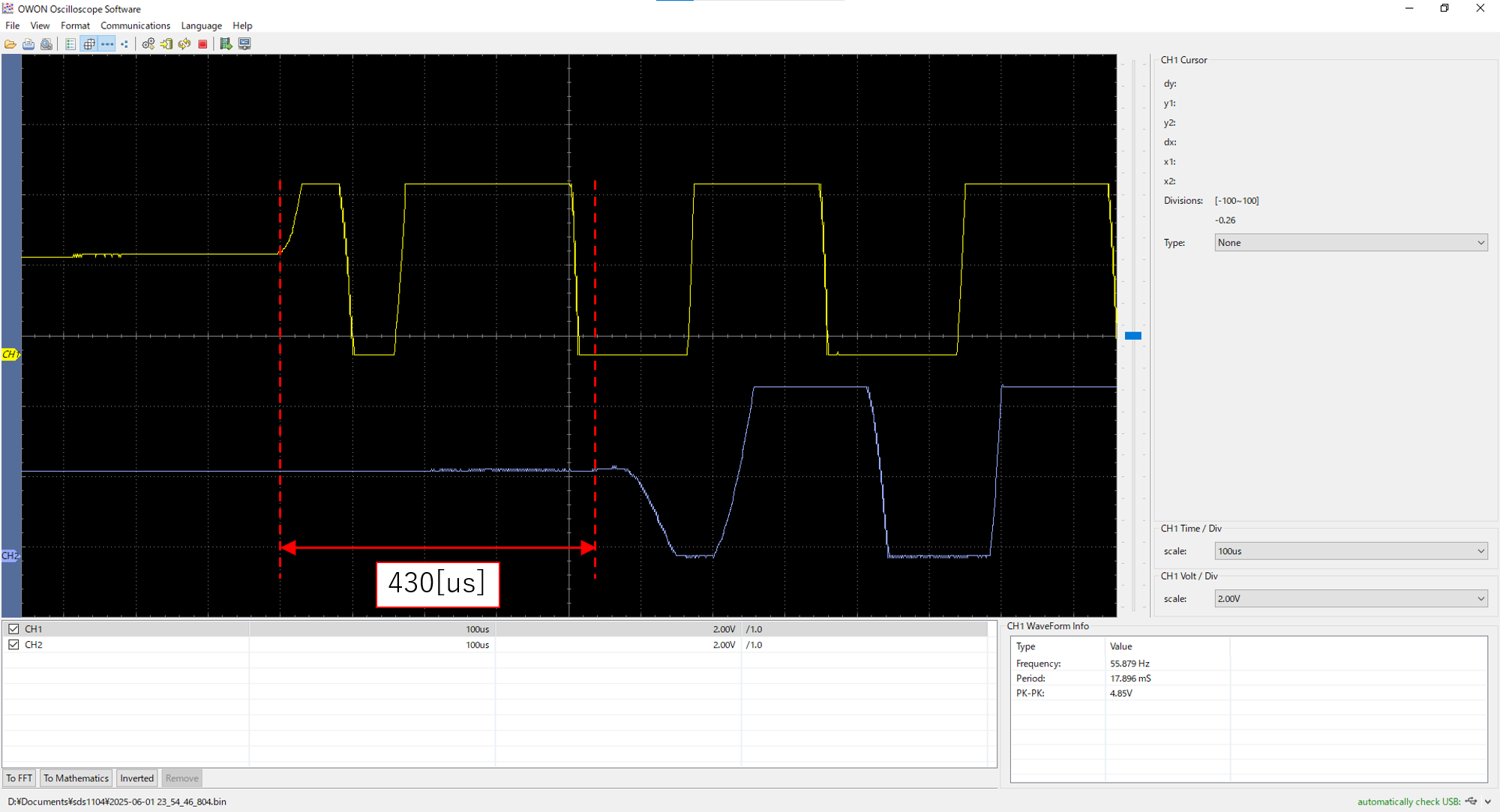
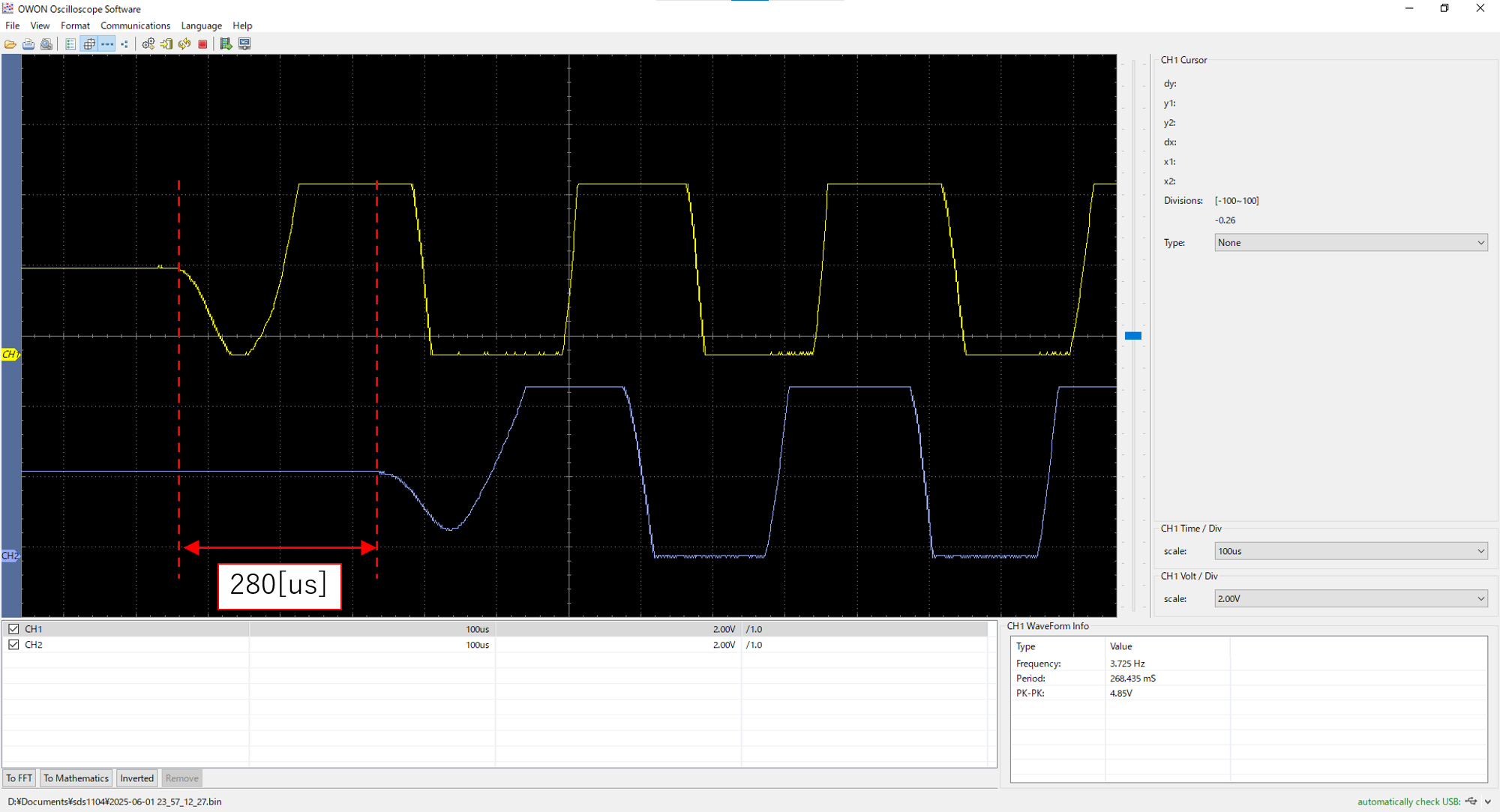
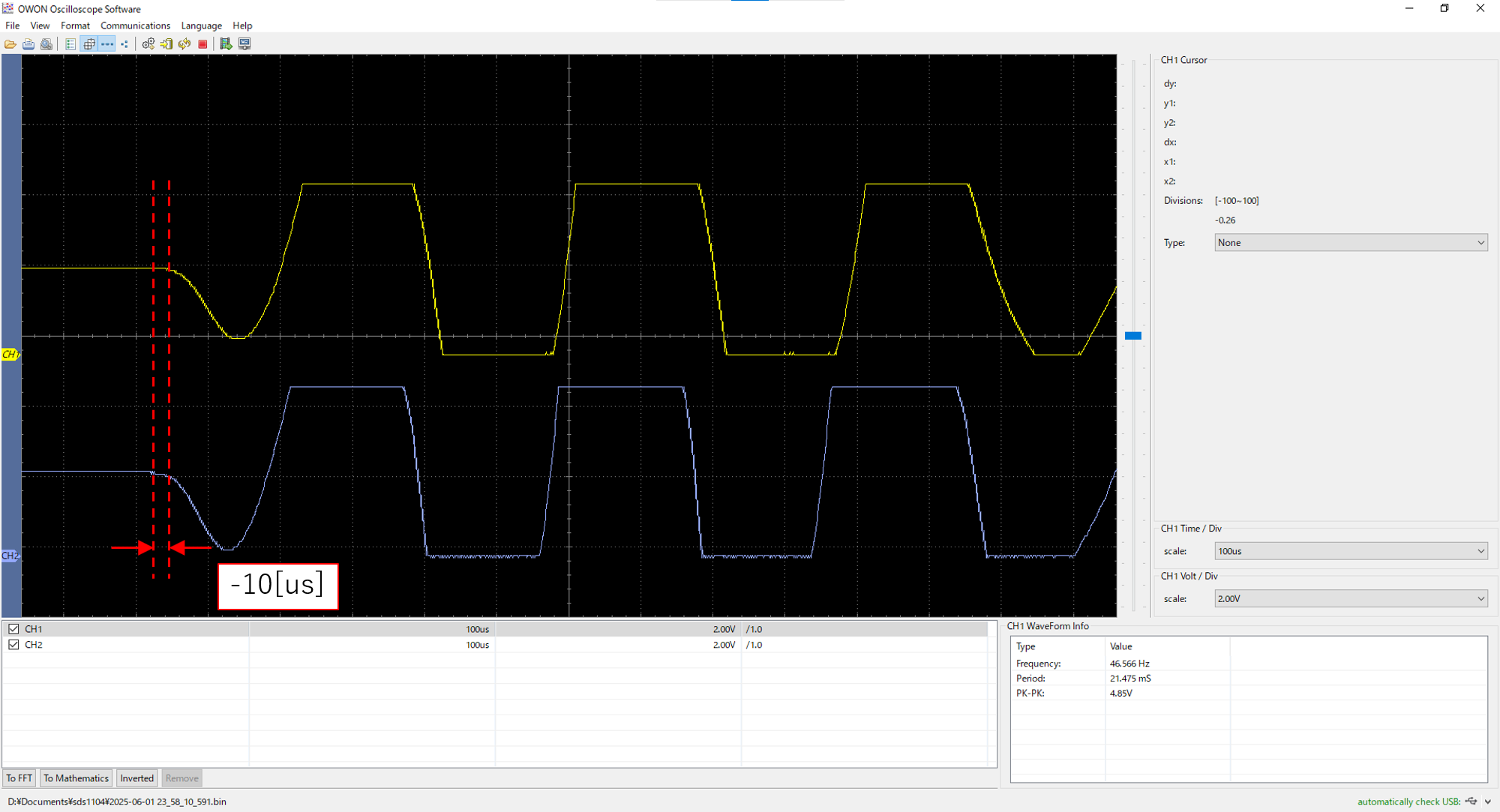
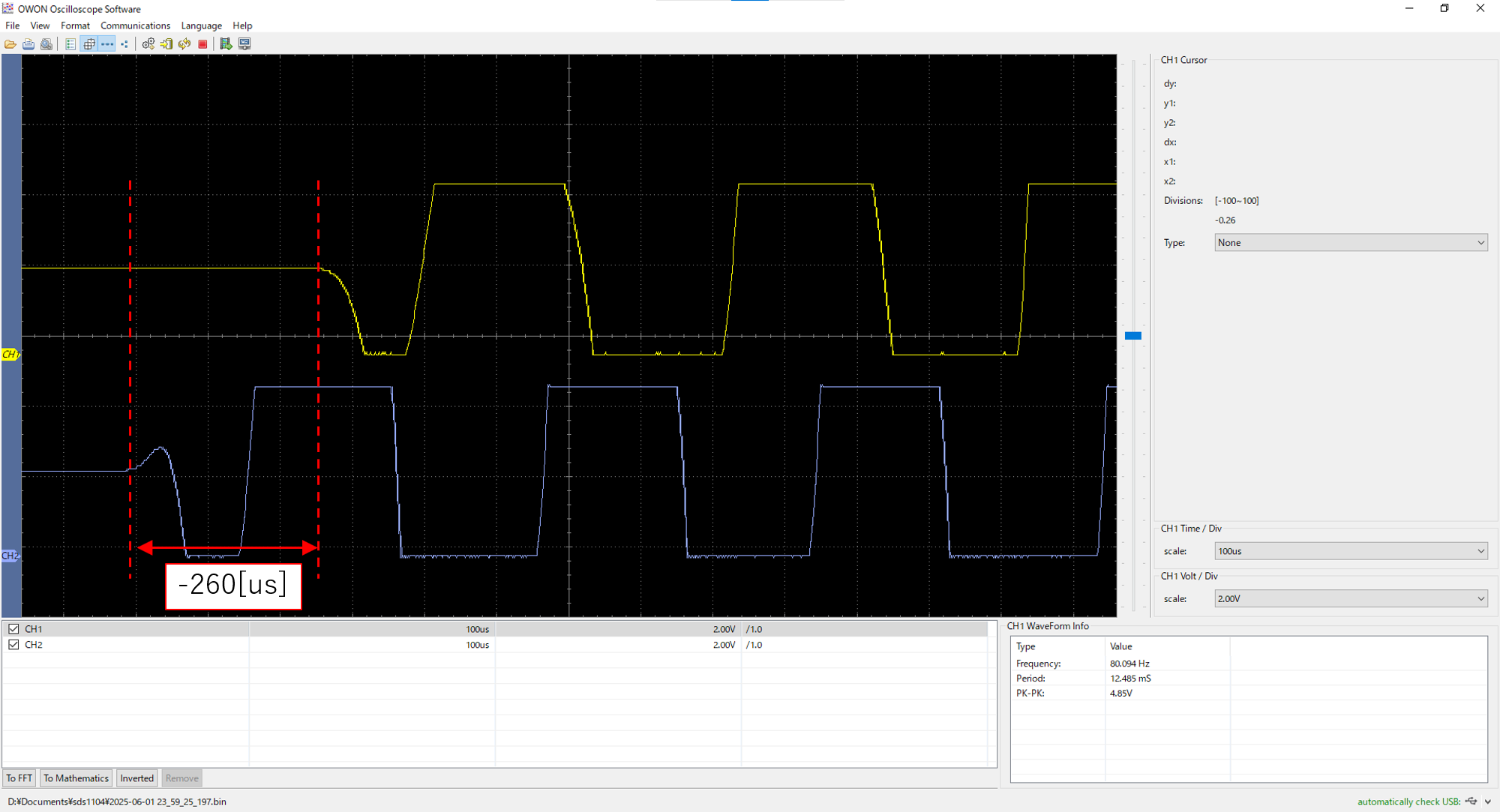
90°点、45°点、0°点、-45°点の音の波形は以下です。
波形が矩形状に見えるのは、音が大きすぎて入力がクリップ(張り付いてしまう状態)しているためで、実際は正弦波に近い形状なはずです。
1ch(黄色)がマイク1、2ch(青色)がマイク2で、div(横軸1マス分の時間)は100usです。
なお、2つのマイク間の音の到達時間差とは、(マイク2の音到達時間 - マイク1の音到達時間)です。
まず90度点の到達時間差から角度を算出します。90度点における音の到達時間の差は340usでした。
元の式(上に書いたものと同じです):
- $\theta$:音源の角度
- $v$:音速(348 m/s)
- $\Delta t$:2つのマイク間の音の到達時間差
- $d$:マイク間の距離(0.15m)
$$
\theta = \sin^{-1} \left( \frac{v \cdot \Delta t}{d} \right) \cdot \left( \frac{180}{\pi} \right)
$$
数値を代入:
$$
\theta = \sin^{-1} \left( \frac{348 \times 430 \times 10^{-6}}{0.15} \right) \cdot \left( \frac{180}{\pi} \right)
$$
まずはアークサインの引数を計算:
$$
\frac{348 \times 430 \times 10^{-6}}{0.15} = \frac{0.14964}{0.15} \approx 0.9976
$$
次にアークサインを計算:
$$
\sin^{-1}(0.9976) \approx 1.502 \text{[rad]}
$$
最後にラジアンを度へ変換します:
$$
\theta = 1.502 \times \frac{180}{\pi} \approx 86.0^\circ
$$
各点の計算結果は以下です。結果からほぼ合っていることが分かります。
マイクと音源の距離が近い、波形の読み取りが簡易的である、カスタネットの位置が合っていないなど、様々な要因で誤差が発生しているのだと思います。ただし、この程度の誤差は本記事の目的上、許容範囲とさせていただきます。
| No. | 音の到達差(µs) | 計算結果(°) | 実際の角度(°) | 誤差(°) |
|---|---|---|---|---|
| 1 | 430 | 86.03° | 90° | -3.97° |
| 2 | 280 | 40.51° | 45° | -4.49° |
| 3 | -10 | -1.33° | 0° | +1.33° |
| 4 | -260 | -37.10° | -45° | +7.90° |
まとめ
本記事ではTDoAの基本的な理論と、実際に動かした結果をまとめました。
今回は静かな環境で実施しましたが、実際の音の波形は様々なノイズが含まれている可能性があります。そのため、パターンマッチングや機械学習などで、対象の音かどうかを調べるプロセスも必要になったりします。
またマイクロ秒オーダーの解析が必要になるため、システムに組み込む場合はコンピュータの性能や機器構成を考える必要があります。