#概要
画像認識にもAttention構造でConvolutionを置き換えて精度が上がるという論文が増えてきたので、今まで出ている論文をまとめようと思う。
まず、事の起こり。
2019年に、そのままSelf-Attentionを画像に入れたら、うまく行くんじゃね？ FLOPｓ数が少ないのに精度が上がるよっていう報告が出始める。
Stand-Alone Self-Attention in Vision Models
（Google Research, Brain Team、 2019年6月、 普通のAttention）
Local Relation Networks for Image Recognition
（Microsoft Research Asia, 精華大学2019年4月、 LR-Net）
今年になってからは、さらに画像用にパーツの（大幅な）調整が始まり、
Exploring Self-attention for Image Recognition
（香港中文大学、Intel Labs 2020年4月、 Patchwise SAN）
ImageNetだけではなく、COCO、Mapillary Vistas、CityScapeでもFLOPｓ数が少ないのにstate-of-the-artだという、特にSemantic segmentationが得意なネットワークも登場
Axial-DeepLab: Stand-Alone Axial-Attention for Panoptic Segmentation
（Johns Hopkins大学、 Google Research, 2020年8月、 Axial attention）
（）内は、著者の所属、発表時期、論文でIntroduceしているネットワークの名前。
CNNからself-Attentionへの流れは、もう止まりそうにない。自然言語で、LSTMっていうのが、Attentionにアッという間に置き換わったのと同じ状況に、画像の方も来た模様。
とはいえ、自然言語は、全然わからないので、調べながら、上の4本の論文を読んでみる。
##そもそも、画像認識ってなんだっけ？
画像認識のタスクは、大量に入力されたデータを分類するタスク。
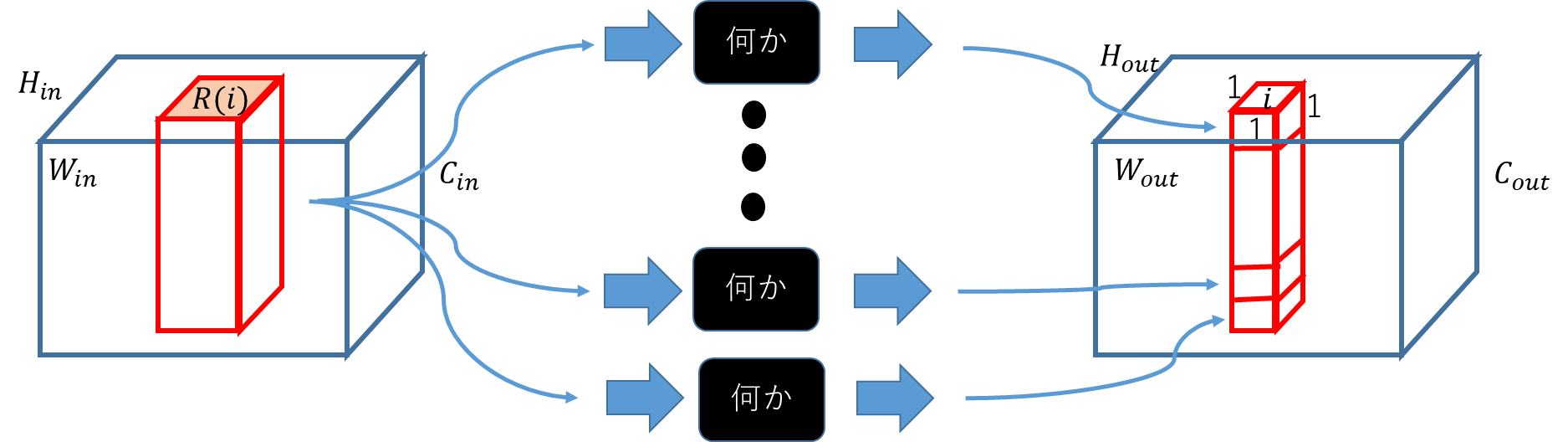
いきなり分類するのは、難しいので、まずは、区別しやすい空間に入力されたモノを変換していく作業をするのが普通。変換も1度ではなく、何度も行う。例えば、変換している最中のデータ$H_{in}×W_{in}×C_{in}$に対し、「何か」のオペレーションをして、$H_{out}×W_{out}×C_{out}$に変換する。当然ながら、途中のデータは$H×W×C$の形を残しておく必要はないけれど、こうしておくと計算効率が良いので、みんなこんな感じでやっている。
ここで、いきなりデータを全部突っ込んで変換させるのは、大変なので、ちょっとだけ入れて、ちょっと変換させると考える方が自然。（扱っているデータが画像なので、遠くのデータはあんまり関係ないだろうという予測。）ということで、入力はspacial position $i$に対して、$R(i)×C_{in}/m$。$R(i)$は、$i$の回りにある$K_1×K_2$のカーネルで、$j∈R(i)$とすると入力は、$x_j$のベクトルの集合と考えられる。入力の$i$と対応する出力$y_i$は、$1×1×d_{out}$。出力のサイズは、$1×1$に限定する必要はないが、現状では、$1×1$が主流。
Convolutional Neural NetworkからAttentionへ
普通のConvolutional Neural Networkを上にあるノーテーションで書くと、
となり、$m=1$、$d_{out}=1$となる。「何か」は$C_{out}$個あり、一つ一つは、$W$という入力と同じサイズのWeightを持っている。このWeightと入力の内積を取った値が出力となる。
$$y_i=\sum_{j∈R(i)} W_j^T x_j$$
この時、$i$ごとに同じWeightを使うことで学習を簡単にしたのが、CNNのすごいところ。
でも、Weightは入力によって調整してくれてる方がうれしい気がする。
⇒ 自然言語の分野で使われているself-Attention構造には、そういう機能がある！
⇒ 画像にも当てはめれば良いんじゃね？
ということで、いろいろ出始めた！
まず、self-Attentionって何よ？
self-Attentionの入力と出力は、Convolutionとほぼ同じ。ただし、Convolutionの時のWeightがself-Attentionでは、入力に依存する。この、Weightの数をHeadの数と呼ぶ。Weightは全て入力に依存するので、並列で作れ、並列で同じ入力に当てることができるので、Embarrassingly parallelにHeadの数だけ出力を作れる。出てきた出力はConcatenateして、さらにLinear変換などでサイズを成型する。最後の成型がなかった場合は下図。
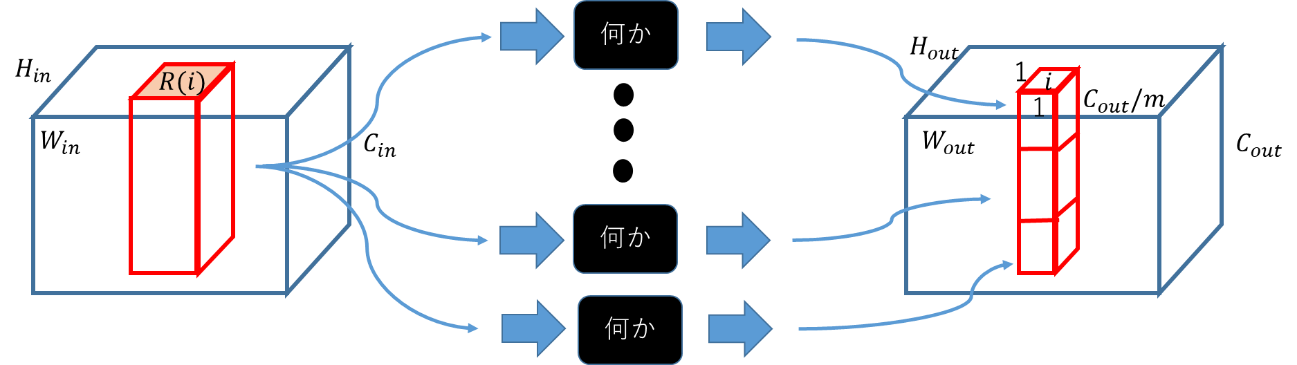
「何か」はHeadの数だけある。
同じWeightを入力のチャンネル方向に分けて組み合わせるChannel Sharingという手法もある。少ない数のSharingであれば、精度は変わらず計算コストが減らせるらしい。Headの数が１である場合は下図。
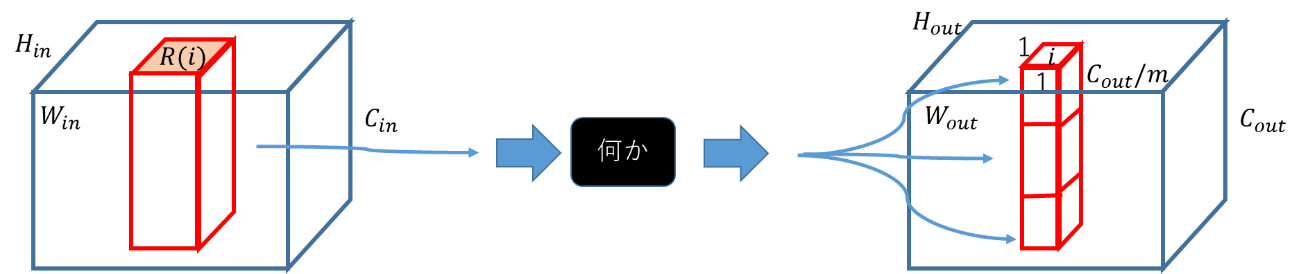
マルチヘッドを並列と考えなければ、Channel Sharingと同じと考えることもできるので、Embarrassingly parallelの場合は、マルチヘッドで、そうじゃないのがChannel Sharingと言うんじゃないかと。すぐに、この辺は言葉が拡張されるので、良くわからない。
どちらにしろ、「何か」の中が、Attention構造となる。
Attention構造自体の解説は、自然言語の方でいくらでもあるけど、自然言語が良くわからない人向けに、画像認識屋さんのための「初めてのAttention」ってのも書いたのでどうぞ。
この記事では、Attentionにself-がついてなくても、全てself-Attentionとする。
Stand-Alone Self-Attention in Vision Modelsを読んでみる
まずは、TransformerのSelf-Attention構造をそのまま画像に持ってきた最初の頃の論文の説明をそのまま追いかけてみる。
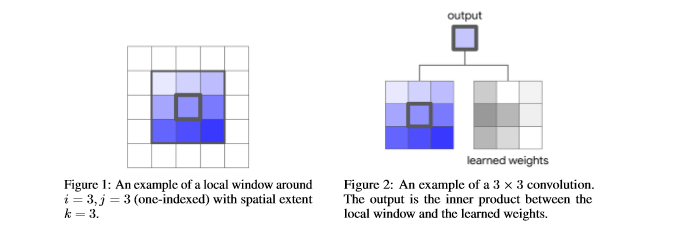
下図は、カーネルの方から見た図。ある場所の回りから、３×３のカーネルを取り出し、学習されたWeightと掛け合わせる。
これに対し、Weightを入力に依存させるAttention構造は、下図。
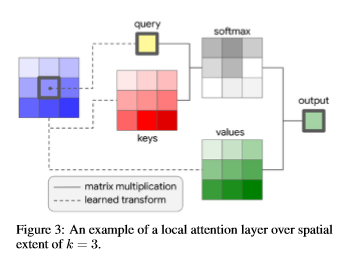
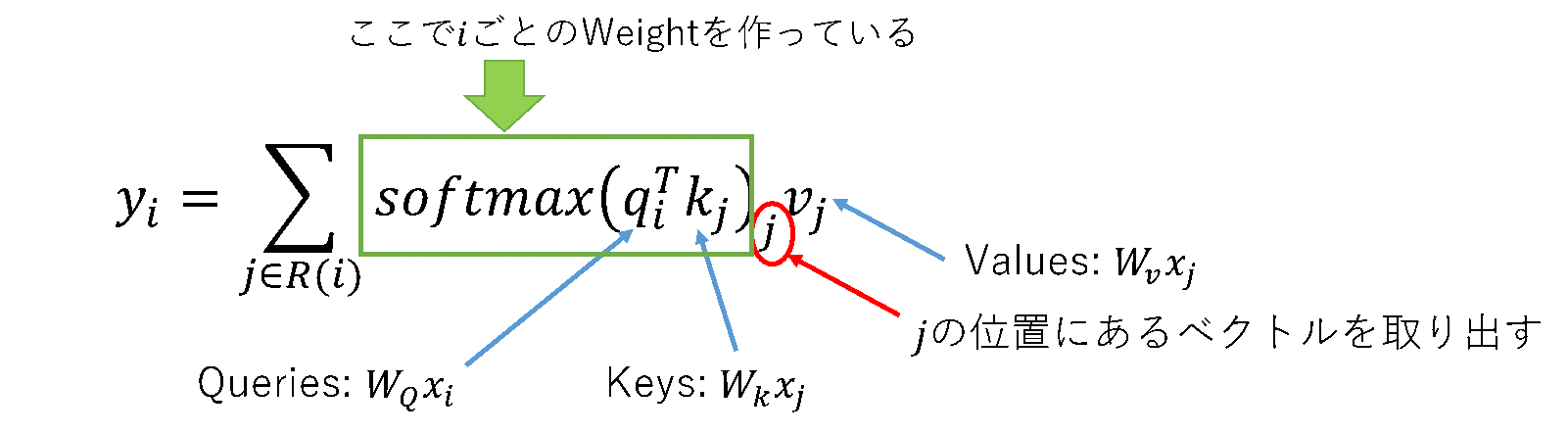
Learned transformとカッコよく言っているのは、普通のAttention構造をそのまま持ってきているので、現状ではただの$１ｘ１$のConvolution。ただ、Attentionの人たちは、これをConvolutionとは言わないで、channel transformationsとか、単にlinear変換という。この変換後の値はデータベースの方から取って来たアイディアからquery, keys, valuesと呼ばれる。画像の方でも、それを引きずる。これを、式で書くと、
これまた、自然言語の方の手法を引きずっているため、出来上がるWeightのチャンネル数は１になるので、$v_j$のlinearの組み合わせが$y_i$となる。
これだけだと、情報がカーネル上のどこにあるかわからない。特徴が中心iの近くにあるのと、遠くにあるのでは、意味が変わる。そこで、自然言語の時と同じくrelative positional encodingとして、$i$との相対距離を表す下図のような$r$を組み込み、
全体は、以下のようになる。
$$ y_i=\sum_{j∈R(i)} softmax(q_i^T k_j+q_i^T r_{j-i} )_j v_j $$
この際、$r$はただの位置を表すoffsetなので、毎回同じになる。
こうなると、$r$を学習させたくなるのが人情で、これ自体を学習で作ってみたり（Axial Attention）、学習で作った行列で変換したり(LR-Net)、そもそもWeightを作るときの学習に位置情報を入れたり(Patchwise SAN)する人が出てくる。
この論文では、自然言語で使っているself-attentionが画像にそのまま適用できるか調べた最初の論文なので、余計な機能は入れていない。それでも、最初の層（STEM）以外は、ResNetのConvをそのままAttentionに変換して、ImageNetのClassificationタスクの精度が上がったと報告している。FLOPｓ数は２９％減、パラメータ数は12％減。
Axial-DeepLab: Stand-Alone Axial-Attention for Panoptic Segmentationを読んでみる
relative positional encodingを拡張して、position biasをkeysとvaluesにもいれると、
$$y_i=\sum_{j∈R(i)} softmax(q_i^T k_j+q_i^T r^q+k_j^T r^k)_j(v_j+r^v)$$
になる。
ここでは、position encodingの$r$は学習で作るので、バイアスと同じような扱いになる。
また、この論文では、遠くまで見ることを主眼にしているので、大きいカーネルサイズを使えるように変更している。
Attentionにしろ、Convolutionにしろ、カーネルサイズが大きくなると学習スペースが増え、パラメータも計算も増えるので、ある程度localにサイズを減らす必要がある。Convolutionの時は、計算制約で3x3のカーネルが多く、逆にサイズを増やしても精度はあまり変わらないが、Attentionなら広げても計算はあまり増えない（Conv比）し精度が上がるらしい。今までは、FilterがFixなのでrepresentation powerが足りなかったからではないかという人もいる（LR-Net）。
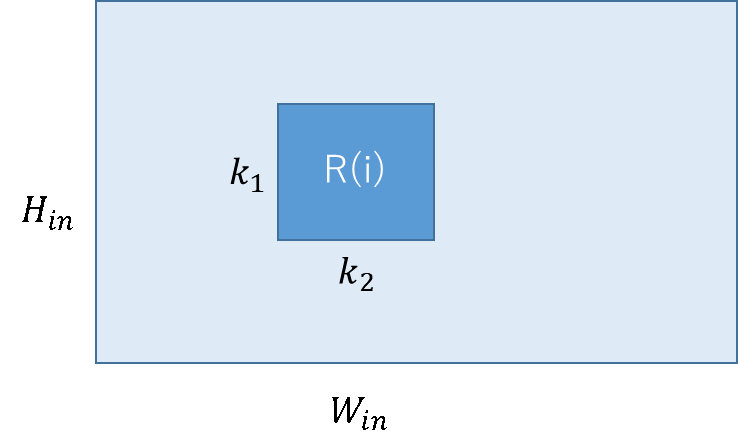
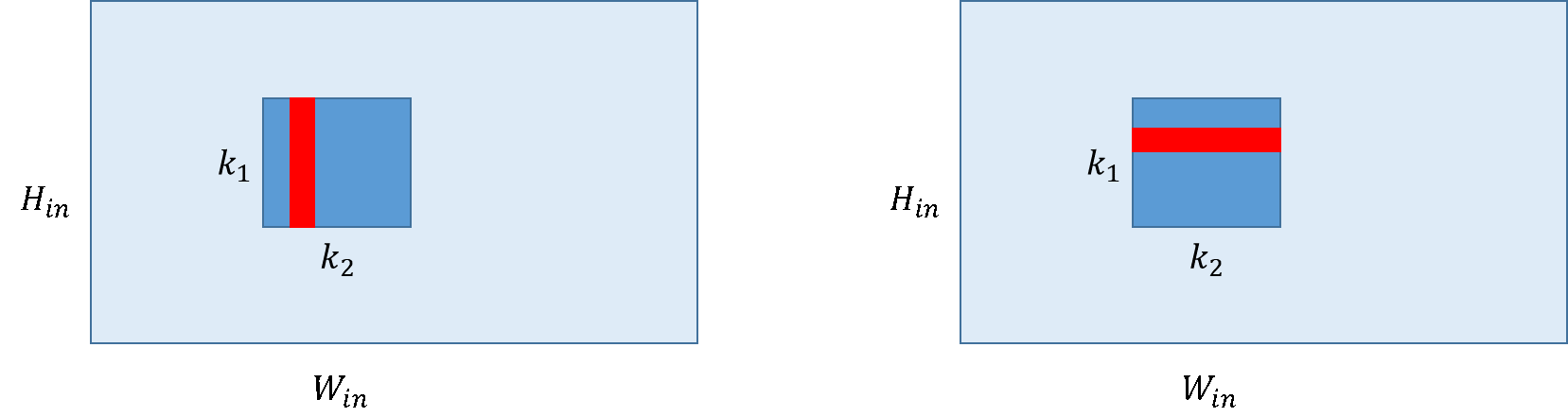
上の図のカーネルをそのまま計算するのではなく、これを下図のように二つにわけて計算するAxial attentionという手法がある。
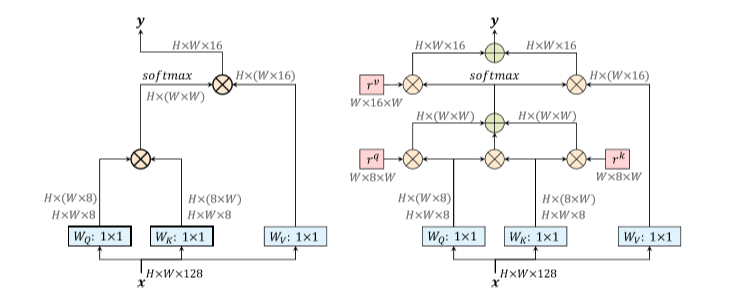
そこで、この論文では、まずは行を丸ごとやってから、次は列をまるごとやることによって遠くまで見ることができるようにした。ResNetのConvをこのPosition encodingとAxial attentionにすることで、ImageNetのclassificationで精度良いのにFLOPｓ数が少ないよ、とのこと。この論文では、さらにCOCO test-dev, Mapillary Vistas, Cityscapeでもstate-of-the-artでFLOPｓ数も少ないと言っている。全体のデータの流れを今までのAttentionと比較した図が、下。カーネルは１行まるごとで1×Wになっている。左が、Position encodingがない普通のAttentionで、右がAxial Attention。
Local Relation Networks for Image Recognitionを読んでみる
ここで、元のAttentionに戻って
ということで、別の手法がこの論文で作られたLR-Net
この論文は、ResNetのConvを全部Attentionで置き換えたらImageNetのclassificationで精度上がったよ、という最初で、1年後にはAxial attentionに負けている。これのデータの流れは下図。
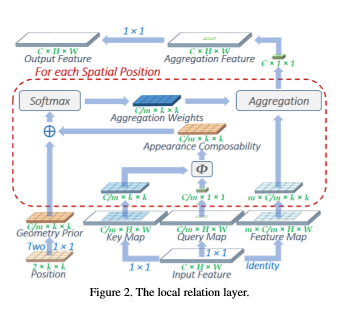
ここで、論文にはChannel Sharingをするとあるが、Weightを作る時にチャンネルの向きには全て並列で作れるので、マルチヘッドと変わりないと思う。スカラ値をベクトルにかけているところまで、並列で行える。
##Exploring Self-attention for Image Recognitionを読んでみる
また、元のAttentionに戻って、
今までの$\delta$は、全てスカラ値を返すためにベクトル$v_j$とは掛け算になっていた（scalar attention）が、$\delta$がベクトルを出すことで、Hadamard product(Elmantwise Mult)をする方法（vector attention）が考えられる。また、Position encodingをするにあたり、$i$とそれ以外だけ見るというのは、Continuousな画像を考える上に不思議なので、全部をまとめて見たい。しかも、全部Linearでバイアスを足さずにやりたい。ということで、考えられたのがPatchwise SAN
$$y_i=\sum_{j∈R(i)} γ(δ(q_i,k_j ))_j \odot v_j $$
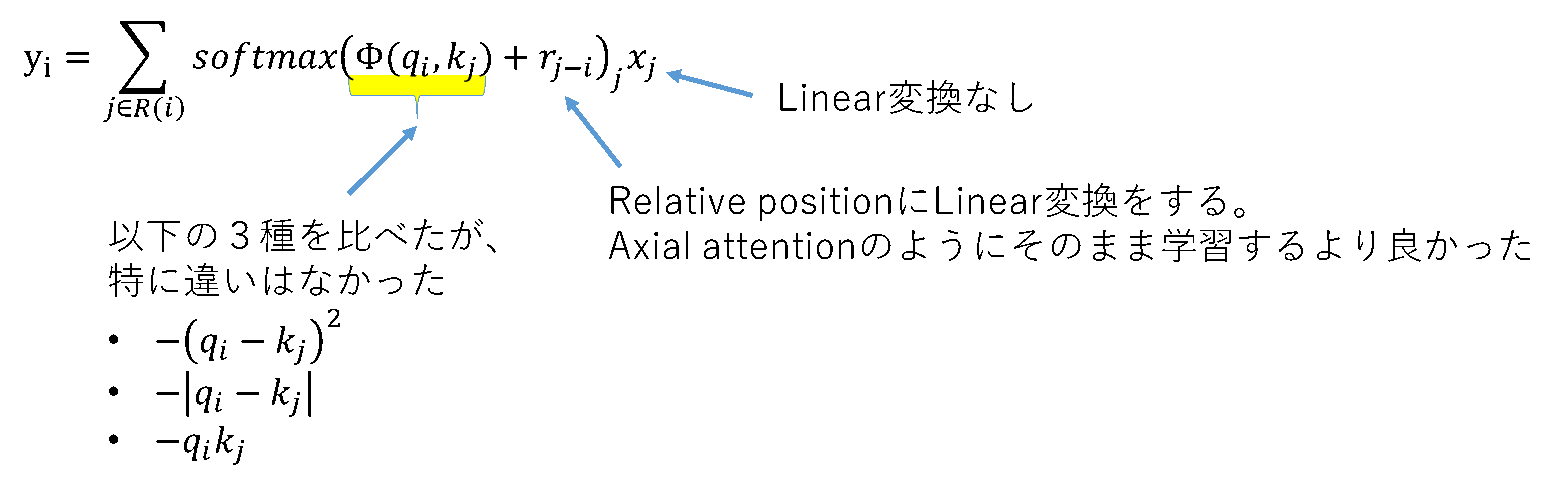
ここで、$\delta$は以下3つ（左から、star-product, clique-product, concatenation）を比較。
このベクトルを$\gamma$を使い、Weightの形にLinear変換する。$v_j$の長さが$C/r_2$であるとすると、Weightのサイズは$k_1 \times k_2 \times C/r_2$となる。
この論文では、マルチヘッドは用いず、Channel Sharingを行うので、同じ入力に対し、Weightの計算は1度だけになる。
実際の比較結果は、以下。
$γ$は、Linear変換をL、ReLUをRとして、試した結果を比較すると、
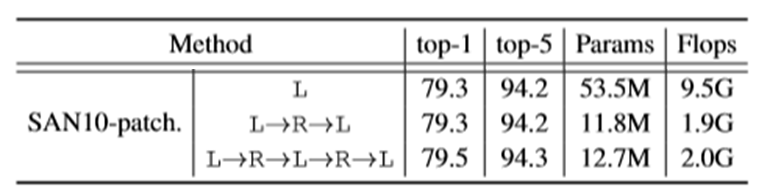
ということで、みんな、ほぼ同じ精度なので、Bottleneck構造でFLOPｓ数を減らした方が良い。
これのデータの流れは下図。
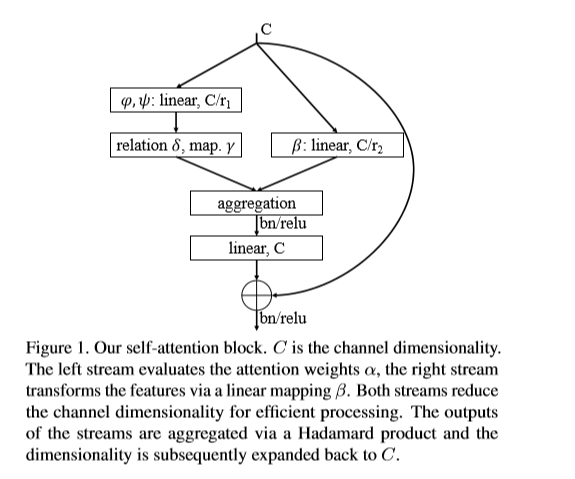
ResNet50を元にConvを変換してImageNetのclassificationをした結果は、同じ時期に出ているAxial attentionより精度は良い。
ということで、気になるのは、Patchwise SANでAxial attentionのカーネルを使うとSemantic segmentationとかの結果は良くなるのか？ とか、他にもいろいろ混ぜ方あるんじゃないか？ とか。
この論文は、こちらの記事がわかりやすい。
Self-Attentionを全面的に使った新時代の画像認識モデルを解説！
まとめ
今まで出てきたすべてをまとめると、
この「何か」は、以下の数式で表せ、
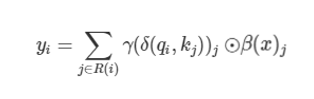
モデルによって、以下を用いる。
ちょっと前に流行っていたSE Layerは実は、Attentionの特別なケースだった模様。
SE Layerが2018年のCVPRでブイブイ言わせていたあとには、すぐさま似たようなネットワーク探索戦争が勃発し、同じ年の超解像分野では、こんな状況（下図）になっているのを考えると、これから1年間は、凄まじい戦いになるのだろう。
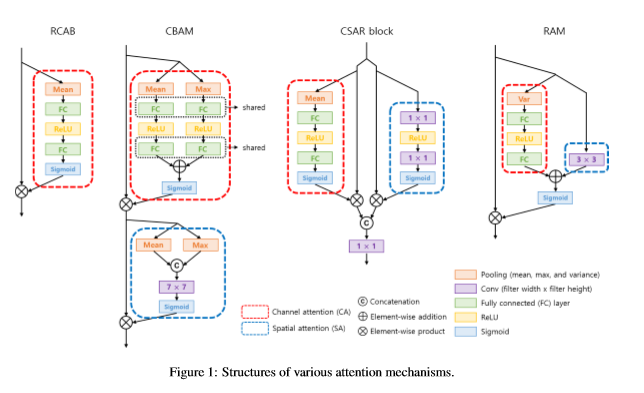
RAM: Residual Attention Module for Single Image Super-Resolutionから