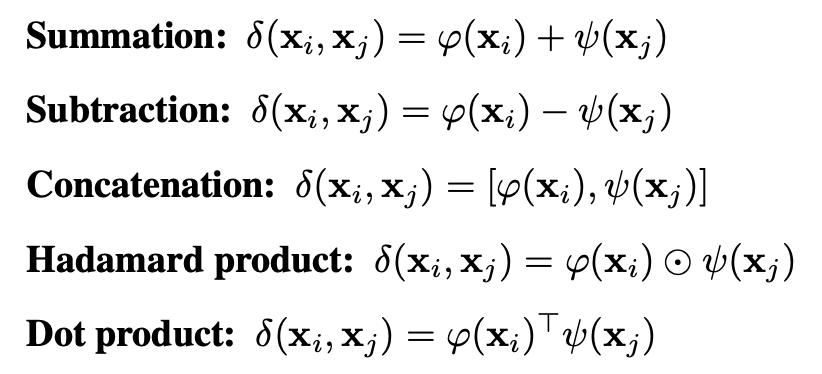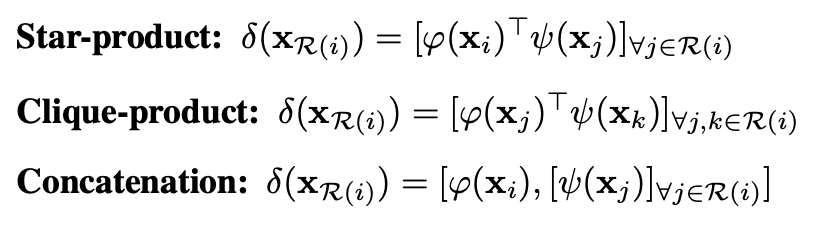- 08/31 (2020): 投稿
- 08/31 (2020): 「畳み込みを一切使わない」という記述に関して、ご指摘を受けましたので追記いたしました。線形変換においては「チャネル間の加重和である1x1畳み込み」を実装では用いています。
- 08/31 (2020): 本論文で提案されているモデルの呼称に関して認識が誤っていたためタイトルおよび文章を一部修正しました。
言葉足らずの部分や勘違いをしている部分があるかと思いますが、ご指摘等をいただけますと大変ありがたいです。よろしくお願いします!(ツイッター:@omiita_atiimo)
Self-Attentionを全面的に使った新時代の画像認識モデルを解説!
近年の自然言語処理のブレイクスルーに大きく貢献したものといえば、やはりTransformerだと思います。そこからさらにBERTが生まれ、自然言語の認識能力などを測るGLUE Benchmarkではもはや人間が13位(2020/08現在)にまで落ちてしまっているほどNLPのAIは隆盛を極めています。これほどまでに発展したNLPですが、その根底にあるものこそがSelf-Attentionの存在です。Transoformerは、それまでNLPで一般的に用いられていたRNN系のモデルを、Self-Attentionに総入れ替えさせたことで性能を大きく向上させました。このSelf-Attentionへの総入れ替えを畳み込みが主力である画像認識でも起こせるのではないか、という疑問に対して大きな希望を与えてくれる論文がとうとうCVPR2020に登場しました。それこそが今回紹介する["Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)]です。ものすごくワクワクします。その全貌を早速見ていきましょう!
[08/31追記] 本論文で提案されているネットワークですが、SANという名前のモデルで提案されたというより「CNN」や「RNN」といった一般的な呼称として「SAN(=Self Attention Networks)」を使っているのではないかというご指摘をいただきました(ありがたいです👏)。私の間違いによるものなので文章を一部訂正させていただきました。なお本記事で**「SAN」とある場合は本論文で提案されているSAブロックを用いているネットワークのことを指しますのでご了承ください**。
流れ:
- 忙しい方へ
- 論文解説
- まとめと所感
- 参考
原論文: ["Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)]
公式実装: https://github.com/hszhao/SAN (PyTorch)
0. 忙しい方へ
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)(改変)
- Self-Attentionで特徴量抽出を行う画像認識モデルだよ
- ResNetの畳み込み層をSelf-Attentionに取り替えたら少ないパラメータ数で性能向上したよ([08/31追記]ただし実装においては、上図中のlinearでPointwiseConvによるチャネル間の加重和を行っています。)
- 本論文でのSelf-AttentionはペアごとのSAとパッチごとのSAの2つに大別されるよ
-
$\boldsymbol{x}_i, \boldsymbol{x}_j$をそれぞれ画像$x$の位置$i$と$j$のチャネル方向のベクトル、$\mathcal{R}(i)$を$i$の近傍点たち、$\alpha$をAttentionスコア関数、$\beta$を線形変換関数とすると、
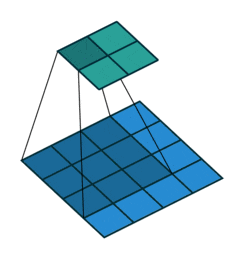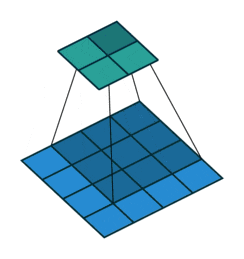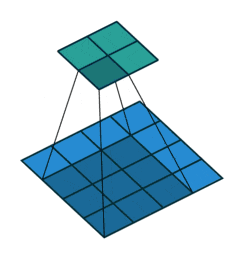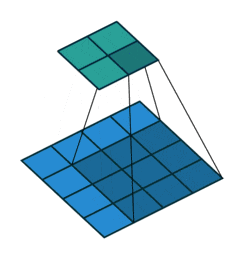
- ペアごとのSA: $\alpha$は、$\boldsymbol{x}_i$と$\boldsymbol{x}_j$だけで計算(e.g.内積など)するよ
\boldsymbol{y}_i=\sum_{j\in\mathcal{R}(i)}\alpha(\boldsymbol{x}_i,\boldsymbol{x}_j)\odot\beta(\boldsymbol{x}_j)- パッチごとのSA: $\alpha$は、$\boldsymbol{x}_i$の近傍点たち$\boldsymbol{x}_j$全て考慮して計算するよ
\boldsymbol{y}_i = \sum_{j\in\mathcal{R} (i)}\alpha(\boldsymbol{x}_{\mathcal{R}(i)})_j\odot\beta(\boldsymbol{x}_j) -
ノイズやPGD攻撃などにも畳み込みよりも高いロバスト性を示したよ
1. 論文「Exploring Self-attention for Image Recognition」解説
1.0 要約
本論文では画像認識における多様なSelf-Attention(=SA)について実験及び評価していきます。その中で大きく次の2つに大別して考えていきます。
- ペアごとのSelf-Attention
- パッチごとのSelf-Attention
その結果、パッチごとのSAで構成されたモデルが畳み込みモデルを大きく上回っています。なんと、Self-Attentionのみで畳み込みを凌駕してしまったようです。驚きですね。(ちなみに「SAよく分からん」という方は、あるピクセルへのSelf-Attentionとは周りのピクセルの値たちの加重和である、と考えるとこの先の説明がわかりやすいと思います。Transformerでは拙著解説でSAに触れていますのでそちらもどうぞ。)
公式実装はこちら(PyTorch)です。
1.1 導入
"A guide to convolution arithmetic for deep learning", Dumoulin, V., Visin, F. (2016)
遡ること30年[LeCun, Y.(1989)]にてCNNが手書き数字の認識を成功させたことから、畳み込みネットワークが画像認識の発展を支えてきました。そこからというものCNNをベースにVGGやResNet、SEモジュールなど様々な工夫を凝らしたアーキテクチャが提案され画像認識界を牽引し続けています。
これらのネットワークは全て離散畳み込み演算を用いたもので、畳み込み演算$\ast$ の式は以下のように定義されます。
(F\ast k)(\boldsymbol{p})=\sum_{\boldsymbol{s+t=p}}F(\boldsymbol{s})k(\boldsymbol{t})
ここで$F, k$はそれぞれ離散関数および離散フィルターで、つまり$F$が画像で$k$がフィルター(a.k.a カーネル)のことです。畳み込みの特徴は、画像$F$全体に同じフィルター$k$が適用されることにあります。この畳み込み演算こそが今の画像認識を支えてきたということは言うまでもありませんが、決して畳み込み演算に欠点がないというわけでもないのです。例えば、畳み込み演算は画像の回転に対して弱かったり、フィルターサイズが大きくなるとそれに伴ってパラメータ数も増えてしまうことなどがあります。そして特に、カーネルよりも外側にある情報を取り込むことはできません。このような欠点を有するConvolutionで画像認識モデルを組み立てるのは果たして最適なのでしょうか。
そんな中、NLPにて猛威を奮っているSelf-Attentionで画像認識モデルを作ることに注目が集まっています。CNNにはなかった特性をSelf-Attentionモデルで実現できるかもしれない、ということです。
本論文では、いろいろな種類のSelf-Attentionを考案し、それぞれが画像認識モデルの基幹部品として使えるのかどうかを評価していきます。Self-Attentionは大きくペアごとのSAとパッチごとのSAの2つに大別されます。
- ペアごとのSA: NLPで使われるようなSAを一般化したもの。
- バッチごとのSA: 畳み込みのように一定の空間内で行うSAのこと。
実験では、いずれのSAも画像認識モデルに効果的なことが分かりました。ペアごとのSAは、対応する畳み込みモデルと比べて少ないパラメータ数&FLOP数で同程度またはより優れた性能を示しています。また、パッチごとのSAではさらに畳み込みモデルを大きく上回っています。例えば、中程度モデルSAN15は、ResNet50よりも37%も少ないパラメータ数およびFLOP数でImageNetで1.1%のゲインを得ています。そして、Self-Attentionによるモデルはロバスト性も高いことが実験でわかりました。
1.2 画像認識におけるSelf-Attention(関連研究)
ここではSelf-Attentionについて触れていきます。元々、機械翻訳や自然言語処理で大きな成功を納めたSelf-Attentionですが、この成功を見て画像認識でもSelf-Attentionを導入しようという考えが芽生えます。
ただし、RNNを完全にSelf-Attentionに入れ替えたNLPに対して、画像認識では当初Self-Attentionは飽くまで畳み込みに加えて使われる補助的なものとして扱われていました。例えば[Hu, J.(CVPR'18)]のSEモジュールに代表されるようなチャネルごとのAttentionや[Woo, S.(ECCV'18)]のCBAMのようなチャネルおよび空間両方をそれぞれ考慮するAttentionなどがあります。これらはいずれも畳み込み演算による特徴量を根底においたものでした。他にも[Wang, X.(CVPR'18)]のNon-local Neural Networksでは畳み込み層の直後にAttentionモジュールを組み込んだり、[Bello, I.(ICCV'19)]では畳み込みとSelf-Attentionを並列に行って結果を連結させています。
本論文の内容により近いものとして、最近の[Hu, H.(ICCV'19)]や[Ramachandran, P.(NeurIPS'19)]があります。この論文両方に共通することは、Self-Attentionの適用範囲を制限した(例えば7x7の範囲内)ということです。それまで特徴マップ全体にSelf-Attentionを適用することが一般的でしたが、この局所的なSelf-Attentionによってメモリや計算量を抑えてかつ性能をあげることができているのです。本論文でもこの結果に基づいて様々なSelf-Attentionを探っていきます。特に、各チャネルに別々に適用されるAttentionベクトルを計算するようなAttention機構を見ていきます。
1.3 Self-Attention Networks
ついにSelf-Attention Networksの実態に迫っていきます。
そもそもCNNでは大きく2つの関数で構成されていることを思い出してください。それは特徴量抽出を行う関数と特徴量変換を行う関数です。それぞれ、「畳み込み層」と「全結合層+非線形活性化関数」のことを指しています。Self-Attention Networkではこのうち特徴量抽出(=畳み込み)の方を変えていくものです。
畳み込み演算とは、重みが固定されているフィルターをフィルターサイズ内の値(=特徴量)に適用して線形結合を得るものです。ここで注目してほしいのは、フィルターの重みが固定されている、ということです。このフィルターの重みは特徴量の値でその都度変わるようなものではありません。そのため、抽出したい特徴量が増えるごとにフィルター数を増やさないといけません。ここで「フィルターの重みが固定されている?いや、フィルターの重み学習されてんじゃんwww固定じゃないしwww」と思った方もいるかもしれませんが、1枚のフィルターで画像を畳み込むときはそのフィルターの重みを一定で画像全体に畳み込みますよね。ピクセル値に関係なく画像全体に一律で同じ値のフィルターをスライドさせるのでパラメータ数も削減できて万々歳、というのが畳み込みでした。あるフィルターはエッジ検出かもしれませんしまた別のフィルターはカド検出かもしれません。ただし、このように1枚のフィルターでは1つの特徴しかつかめません。そのため、たくさん特徴が欲しいときはそれに応じてフィルターの枚数を増やさないといけないということです。
一方でこれから説明するSelf-Attentionではその重みの値を入力の(ピクセル)値によって変化させちゃおうぜ的なニュアンスが入っています。ピクセル値によって畳み込み時にも最適な重みが計算できたらそれの方が強そうなのは感覚的にも合点がつきます。
1.3.1 ペアごとのSelf-Attention
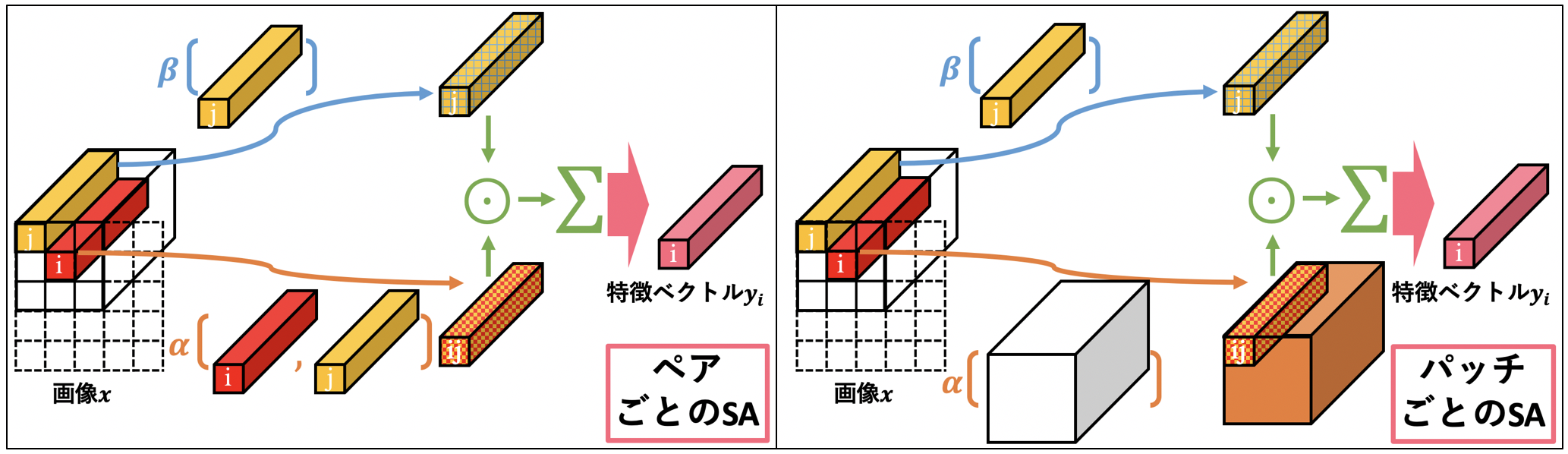
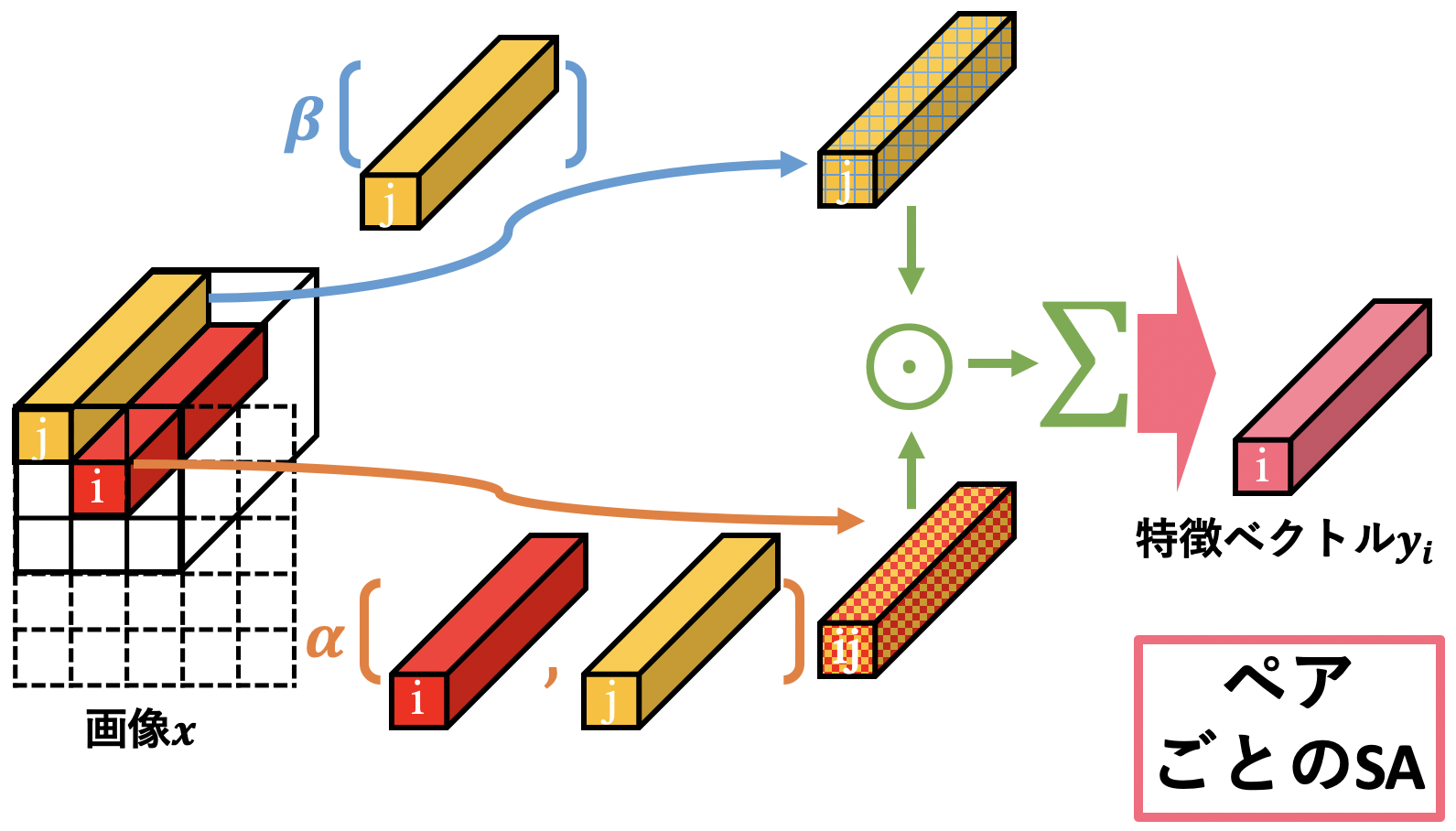
まずはペアごとのSelf-Attentionを見ていきましょう。式は次のようになります。この式のイメージ図として上に図示しました。
\boldsymbol{y}_i=\sum_{j\in\mathcal{R}(i)}\alpha(\boldsymbol{x}_i,\boldsymbol{x}_j)\odot\beta(\boldsymbol{x}_j)
ここで$\odot$は要素積(a.k.a アダマール積)で、$i$は空間的な場所を表すインデックスです( $\boldsymbol{x}_i$ は特徴マップの位置 $i$ の特徴ベクトル、ということ)。$\mathcal{R}(i)$は位置$i$の近傍ピクセルの位置インデックスの集合となっています(近傍を注目ピクセルの周囲3x3とすると、$\mathcal{R}(i)$は9個のインデックスを含む集合ですね)。上式は単に、位置$i$の特徴ベクトル$\boldsymbol{y}_i$は、周囲のピクセルたち$\mathcal{R}(i)$の特徴ベクトル$\beta(\boldsymbol{x}_j)$を$\alpha(\boldsymbol{x}_i,\boldsymbol{x}_j)$の値で加重和する、という感じです。この加重和$\alpha$を決定するのにピクセル値を用いているので、入力値によってここの重みが変化しています。
それでは関数$\alpha$と関数$\beta$の中身はどうなっているんだ、ということになるわけですが、$\beta$は単純なのでそちらからささっと片付けます。$\beta$は$\boldsymbol{x}_i$を線形変換する関数(実装ではPointwise Conv.)です。Transformerで使われているSelf-Attentionで言えば、$\beta(\cdot)$は$V$に変換する線形変換$W_{V}$に該当しています。(Transformerの拙著解説はこちら)
一方で$\alpha$についてはもう少し詳しく説明をしていきます。まず、$\alpha$とは$\beta$たちを加重和させるための係数を決定する関数ですが、これを少し以下のように分解します。
\alpha(\boldsymbol{x}_i, \boldsymbol{x}_j)=\gamma(\delta(\boldsymbol{x}_i, \boldsymbol{x}_j))
新たな記号が出てきてしまいました。ここで、$\delta(\cdot, \cdot)$は関係関数と呼ばれ、$\boldsymbol{x}_i$と$\boldsymbol{x}_j$を用いて1つのベクトル(またはスカラー)を出力してくれます。そして関係関数$\delta$による出力が$\beta(\boldsymbol{x}_j)$と計算できるように $\gamma(\cdot)$は$\delta$の出力を変換してくれるマッピング関数 です。言わば、形を整えるだけの関数みたいなものですね。なので、関係関数$\delta$が$\alpha$の肝となっています。
1.3.1.1 マッピング関数について
このマッピング関数$\gamma$の存在意義がいまいちピンとこないかもしれませんが、これによって関係関数$\delta$の出力は$\beta(\boldsymbol{x}_j)$と同じ形でなくてもよくなるので、マッピング関数$\gamma$のおかげで幅広い関係関数$\delta$を考えることができるようになる、という利点が出てくるのです。本論文で考える$\gamma$はLinear -> ReLU -> Linearの形をとるようにしています。
1.3.1.2 関係関数について
それでは関係関数$\delta$を探していきましょう。関係関数$\delta$とは、$\boldsymbol{x}_i$と$\boldsymbol{x}_j$を表現するベクトル(orスカラー)を出力してくれる関数のことでした。入力の2つのベクトルをうまく捉えられているような関数が良さそうですね。論文中ではその候補として次の5つが挙げられています。ここで$\varphi$と$\psi$はMLPのような学習可能な関数です。
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
足し算や引き算、連結など基本的な演算たちですね。次元について少し補足しておくと、連結(Concatenation)においては出力は入力の2倍となり、内積(Dot product)においては出力はスカラーになります。NLPなどでSelf-Attentionに馴染みのある方ならこの内積を見て思うことがありませんか。そうです、この内積がまさに一般的なSelf-Attentionです。Transformerの例で言えば$Q^\intercal K$に該当するので、$\varphi(\cdot)$と$\psi(\cdot)$はそれぞれ$W_{Q}$と$W_{K}$に該当しますね。こう考えると、本論文では$Q^\intercal K$だけでなく$Q-K$や$[Q,K]$なども考えているので一般的な内積によるSAよりも適切なSAを探すことが出来そうですね。
\boldsymbol{y}_i=\sum_{j\in\mathcal{R}(i)}\gamma(\delta(\boldsymbol{x}_i, \boldsymbol{x}_j))\odot\beta(\boldsymbol{x}_j)
再び式に戻ると、意味がすんなり入ってくるかと思います。$\alpha(\cdot,\cdot)$は展開しておきました。この式によって、$\boldsymbol{x}_i$の特徴ベクトル$\boldsymbol{y}_i$は、
- $\boldsymbol{x}_i$の周りの$\boldsymbol{x}_j$を線形変換した$\beta({\boldsymbol{x}_j})$を加重和
- 加重和の重みは$\boldsymbol{x}_i$と$\boldsymbol{x}_j$の関係によって決定
ということがわかりますね。
1.3.1.3 位置エンコーディング
パッチごとのAttentionに移る前に一点だけ付け加えておくことがあります。ペアごとのAttentionでは、加重和の重み係数$\alpha(\boldsymbol{x}_i, \boldsymbol{x}_j)$の計算に場所$i$と$j$以外の情報を取り込むことができていません。空間的な文脈をもう少し入れるために、特徴マップに位置情報をねじ込んでみます。位置情報は、
- 特徴マップの縦軸と横軸両方を[-1,1]の座標系と見立ててピクセルの座標(=2次元ベクトル)を獲得
- そのまま座標を使うのではなく、学習可能な線形関数で2次元ベクトル$\boldsymbol{p}_i$に線形変換
- $\delta(\boldsymbol{x}_i,\boldsymbol{x}_j)$の出力に$[\boldsymbol{p}_i-\boldsymbol{p}_j]$ベクトルを連結させて$\gamma(\cdot)$に流す
こうすることでSelf-Attentionに相対的な位置$[\boldsymbol{p}_i-\boldsymbol{p}_j]$を考慮させ、空間的な文脈を考慮できるようになります。
1.3.2 パッチごとのSelf-Attention
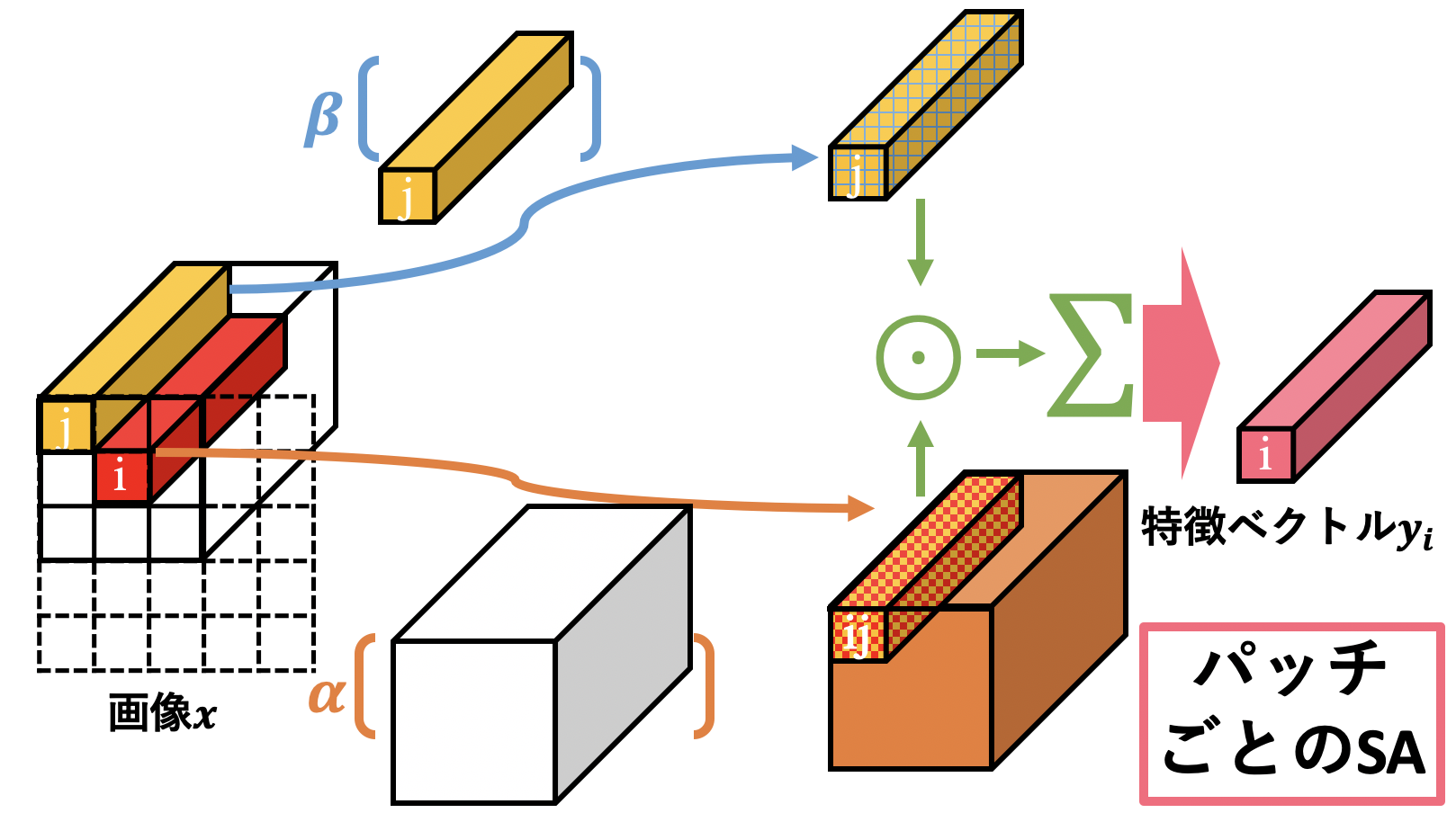
それでは本論文で取り扱うもう一つのSelf-Attentionである、パッチごとのSelf-Attentionを見ていきましょう。といっても、ペアごとのSAとほぼ同じなので意味は分かり易いと思います。式は次のようになります。今回もイメージ図として上に用意してみました。ペアごとのSAとの変更点としてはAttentionスコアがパッチ全体で計算されているというところだけです。
\boldsymbol{y}_i = \sum_{j\in\mathcal{R}(i)}\alpha(\boldsymbol{x}_{\mathcal{R}(i)})_j\odot\beta(\boldsymbol{x}_j)
ここで、$\boldsymbol{x}_{\mathcal{R}(i)}$はパッチ$\mathcal{R}(i)$内のベクトルたち になっています。 $\alpha(\boldsymbol{x}_{\mathcal{R}(i)})_j$は$\alpha$による出力テンサー内の位置$j$のベクトルのこと。この位置$j$は実際の特徴マップ内の位置$j\in\mathcal{R}(i)$に対応しています(位置$j$の特徴ベクトル$\boldsymbol{x}_j$にも対応しているということ)。
ペアごとのSAとの違いは、$\beta(\boldsymbol{x}_j)$の加重和の重み係数$\alpha(\cdot)$はパッチ内の全ての値を考慮して一気に決定している、というところにあります(ペアごとのSelf-Attentionでは2つのベクトル($\boldsymbol{x}_i$と$\boldsymbol{x}_j$)しか考慮していない)。パッチごとのSAの方がパッチない全体を考慮した重み係数となっているので、強そうですよね。
ペアごとのSAと同じく$\alpha$は$\gamma(\delta(\boldsymbol{x}_{\mathcal{R}(i)}))$と分解され、$\gamma(\cdot)$は形状を整える関数で $\delta(\cdot)$が重要な関係関数 です。本論文で考えられている関係関数は以下の3つです。
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
1.3.3 Self-Attention Block
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)(改変)
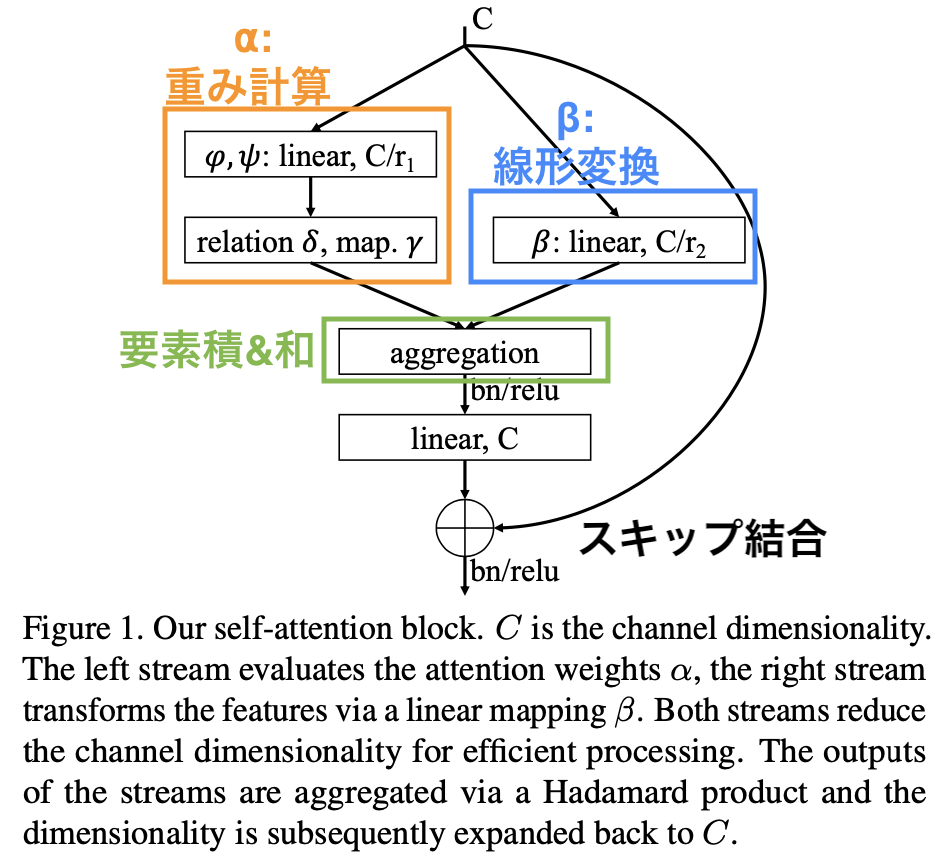
それではSelf-Attentionブロックの全体図を見てみましょう。ここまでの内容を理解していれば上図は見たままでわかると思います。まずチャネル数Cのテンサーが3つに分かれています。右はただのResidual Blockのようなスキップ結合です。左は重み$\alpha$の計算で、中央は$\beta$による線形変換です。ここで、$\alpha$と$\beta$での計算ではチャネル数を$\frac{C}{r_1}$や$\frac{C}{r_2}$のように削減させています(SAGAN[Zhang, H.(2018)]で使われるようなSAでもチャネル数を削減させることで計算量を減らしています)。デフォルト値はそれぞれ$r_1=16, r_2=4$となっています。続いてaggregationで$\alpha$と$\beta$の要素積と和を行なうことでSAの計算が終了します。あとはバッチノーム、ReLU、線形変換を行って最終的なチャネル数Cに戻してResBlock同様にスキップ結合と足し算します。もう一度バッチノームとReLUを通したらこのブロックは終了です。
Self-Attentionブロックの実装はこちらです。また、aggregationのところの実装をもっと知りたい方はこちらの実装を参照してみてください。
1.3.4 ネットワークのアーキテクチャ
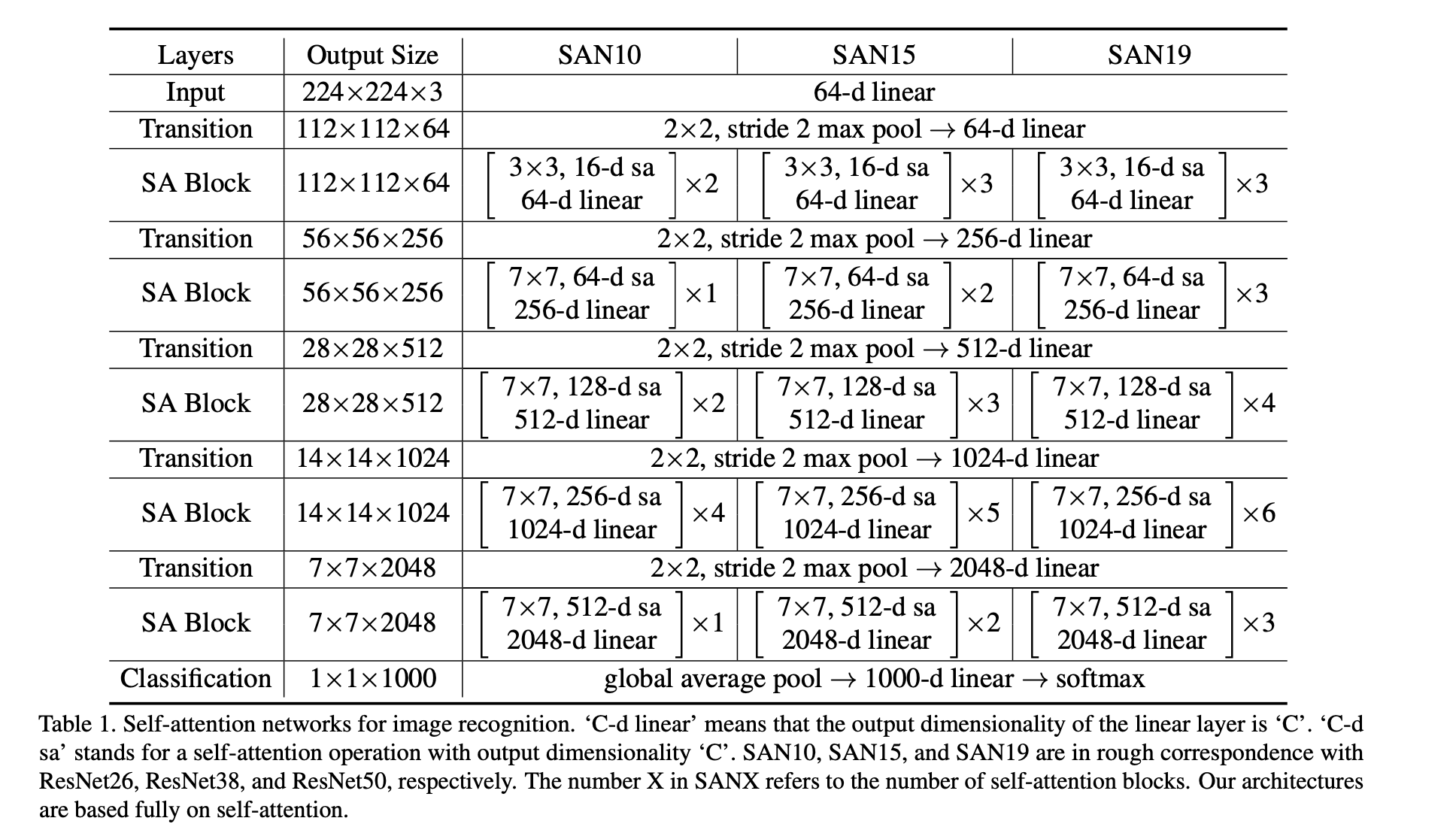
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
先ほどのSAブロックを用いてネットワークを作っていきましょう。と言っても、上表を見てもわかるように基本的にResNetを模したネットワークとなっており、5ステージで構成されています。ステージごとに画像サイズが小さくなっていきます。あとは上表を見て組み立てるだけです。SANXのXはSAブロックの数で決まっており、SAN10/15/19はそれぞれResNet26/38/50に大体対応しています。補足をすると、SAブロックの3x3や7x7はSAの式で言うと近傍$\mathcal{R}(i)$の範囲のことです。またTransitionは、MaxPool2x2で空間的なサイズを半分にして Linearでチャネル数を拡張させる感じです。
1.4 比較
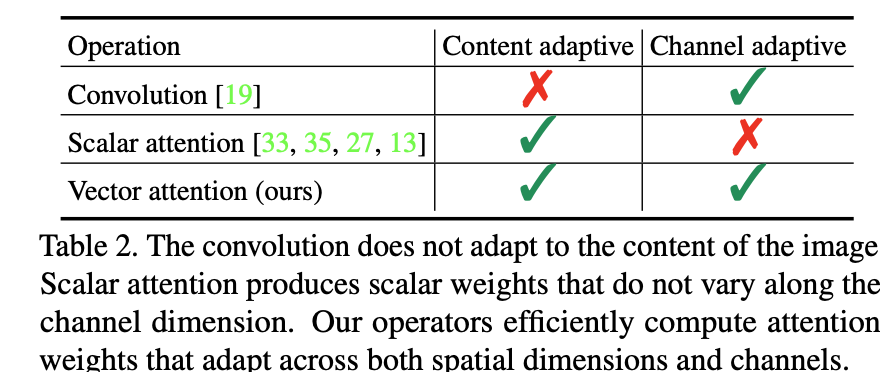
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
実験の前に一旦他手法との比較を行います。手法は次の3つです。
- 畳み込み
- スカラーAttention
- ベクトルAttention(本論文の手法)
「Content Adaptive」とは重みが各場所の値を考慮しているかを示しており、「Channel Adaptive」とはチャネルごとに重みが異なるかを示しています。これらを各手法についてまとめたものが上表です。
畳み込みについては今までも述べたように、固定値のカーネルを画像1枚全体にスライドさせるのでContent Adaptiveとは言えません。一方でチャネルごとにカーネルが存在するのでChannel Adaptiveとは言えます。
続いてスカラーAttentionですが、Transformerで用いられる内積のAttentionが代表的な例です。式で見てみると、$\boldsymbol{y}_i=\sum_{j\in \mathcal{R}(i)}(\varphi(\boldsymbol{x}_i)^\intercal\psi(\boldsymbol{x}_j))\beta(\boldsymbol{x}_j)$となりますが、内積をしているので$(\varphi(\boldsymbol{x}_i)^\intercal\psi(\boldsymbol{x}_j))$の部分はスカラーとなっています。このスカラーはピクセル値によって異なるためContent Adaptiveではあるものの、スカラーであるが故にチャネル方向にはこの値が一定で適用されてしまうのでChannel Adaptiveではありません。
そして本論文のベクトルAttentionですが、ここまでで見てきたように重みは ピクセル値によって決定されます(=Content Adaptive) し、その重みはチャネル方向に伸びるベクトル(=Channel Adaptive) になっていますので2つの良いとこどりを見事に達成しています。
1.5 実験
実験はImageNetで行います。ImageNetは128万枚の学習データと5万枚の評価用データを含みます。ResNetのような畳み込み中心のモデルと比較することでSelf-Attentionの有用性を見ていきます。
1.5.1 実験条件
| パラメータ | 値 |
|---|---|
| エポック数 | 100 |
| 学習率 | 0.1 |
| 学習率スケジューラ | Cosカーブ |
| データオーギュメンテーション | クロップ+水平反転+正規化 |
| バッチサイズ | 256 |
| ラベルスムージング係数 | 0.1 |
| オプティマイザー | SGD |
| モーメンタム | 0.9 |
| 重み減衰率 | 1e-4 |
1.5.2 CNNとの比較
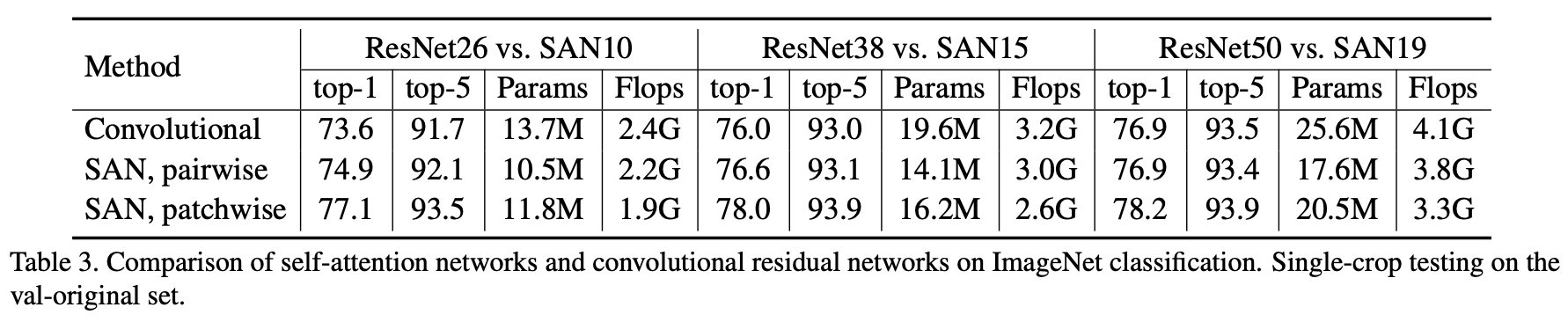
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
畳み込み/ペアごとのSA/パッチごとのSAの3つで比較をしています。ここで、ペアごとのSAにはSubtraction(差)をパッチごとのSAにはConcatenation(連結)を用いています。このSubtraction/Concatenationは次の実験5.3で得られた結果をもとに
まず、畳み込みとペアごとのSAを見比べてみましょう。明らかにペアごとのSAの方が畳み込みよりも高い精度を出しています。しかもパラメータ数およびFLOPs数はペアごとのSAの方が低いです。Self-Attentionすごいですね。パッチごとのSAはどうでしょうか。パッチごとのSAはもう畳み込みをぶちのめしてしまっています。特に、SAN10はResNet26よりも40%も少ないパラメータ数とFLOPs数で高い精度を叩き出しています。SAN15もResNet50よりも37%も少ないパラメータ数とFLOPs数で高い精度を出しています。
1.5.3 対照実験
ここからはモデルの各パーツについて様々な値で実験を行っていきます。デフォルト値として使用されているものにオレンジ色で下線を引いております。
1.5.3.1 関係関数
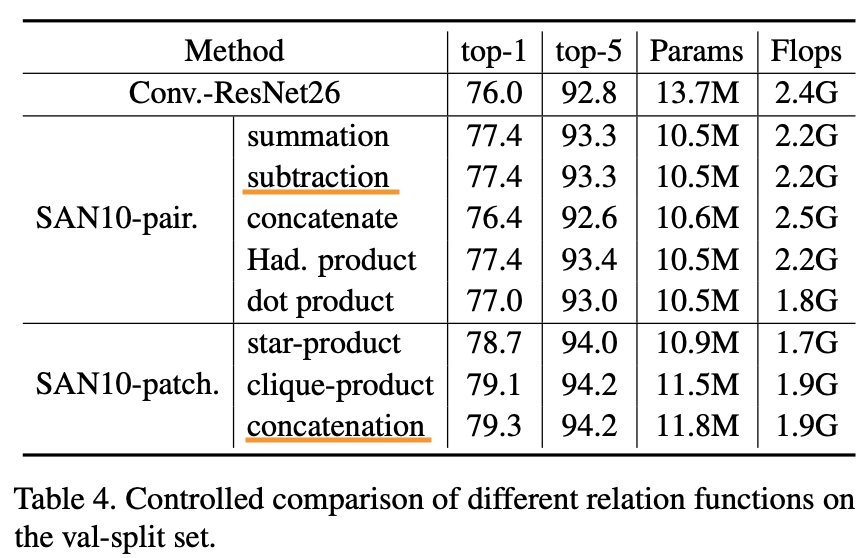
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
ここではペアごと/パッチごとのSAにおける関係関数$\delta$について比較実験を行なっています。つまりどうやってAttentionスコアを算出するのが一番いいか、ということを見ています。まずペアごとのAttentionでは和/差/要素積(=Had. Product)がSAで一般的に使われる内積よりもいいですね。この結果から内積のようなスカラーAttentionスコアよりもベクトルAttentionスコアの方が良いと言えます。ベクトルAttentionスコア恐るべし。一方でパッチごとのAttentionに関しては、まずペアごとのSAよりもパッチごとのSAの方がより高い精度を示しています。また連結(=Concatenation)がわずかに他の手法よりも勝っていますね。この結果から1.5.2ではペアSAには差を、パッチごとのSAには連結をデフォルトとして用いているのですね。
1.5.3.2 マッピング関数
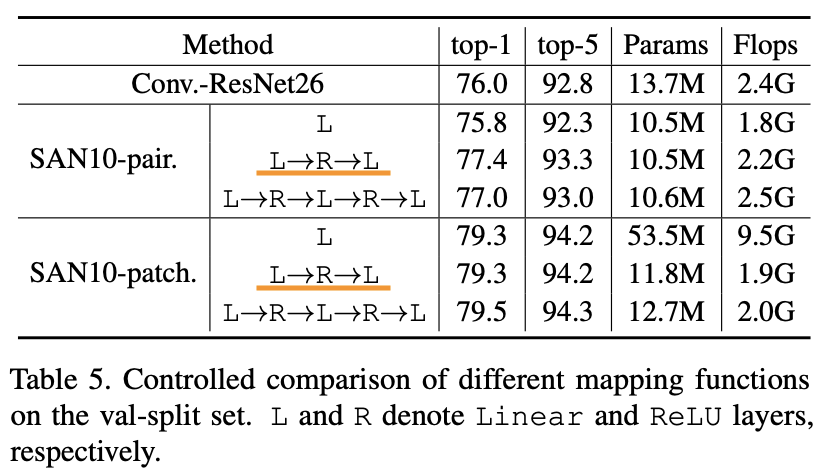
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
続いて関係関数$\delta$の出力の形状を$\beta$の出力と合わせるためのマッピング関数$\gamma$について考えていきます。上表がその結果ですが、この表から次の2つが言えます。ここでLは全結合層、RはReLUを示しています。
- ペアごとのSAでは2層が一番良い
- パッチごとのSAでは性能にあまり差が出ない
ここで勘の良い方は、パッチごとのSAで一層のときのパラメータ数が多層のものに比べてずば抜けて多いことに不思議に思ったかもしれません。これは、多層になるとボトルネック構造を使えるのでそこでパラメータ数を削減できるということです。これらを踏まえてペア/パッチにかかわらずこちらのモデルではデフォルトで2層のマッピング関数$\gamma$を使用しています。
1.5.3.3 線形関数たちの有用性
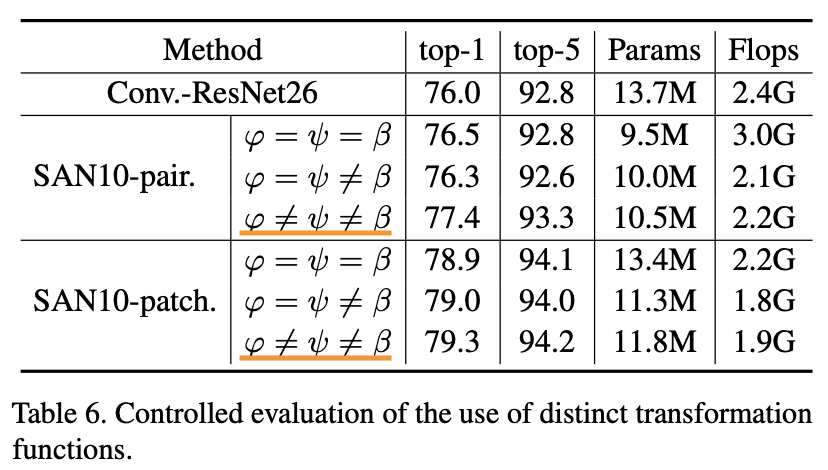
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
ここでは、関係関数$\delta$を計算する前の線形関数$\varphi, \psi$と加重和するための線形関数$\beta$について考えます。これらはそれぞれTransformerでいうSAの前に入力を線形変換する$W_Q, W_K, W_V$と考えると分かり易いかもしれません。この$W_Q, W_K, W_V$が別々で必要なのかそれともQ/K/Vを出すときに1つの$W$だけ(つまり、$W_Q=W_K=W_V$)でいいのかなどを考えていきます。上表を見ると$\varphi \neq \psi \neq \beta$がペア/パッチいずれでも良いことがわかりますね。つまり、$\varphi, \psi, \beta$はしっかりと別々で用意した方が良いようです。
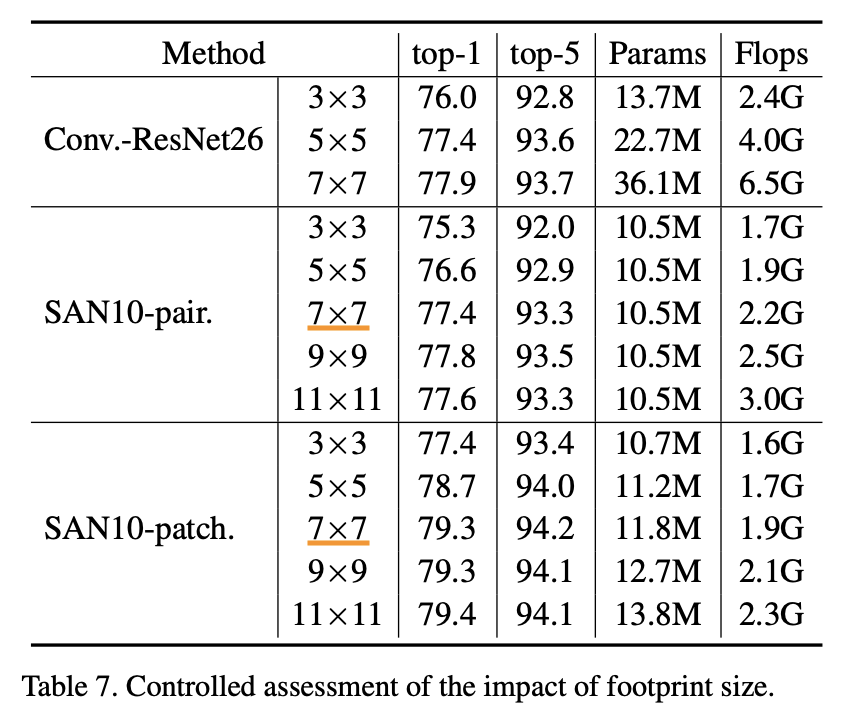
1.5.3.4 近傍点の範囲
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
Attentionを計算する際に、ある注目点$i$の周囲どこまでを考えれば良いのかを考えます。上表が様々なサイズで考えた場合の結果です。結論を言うと7x7をデフォルトとしています。理由は、次の2つです。
- SANにおいて7x7より大きくしても精度は頭打ち
- サイズを大きくしていくと計算コストおよびメモリが増えてしまう
これらを考慮して7x7がベストな選択であるとしています。
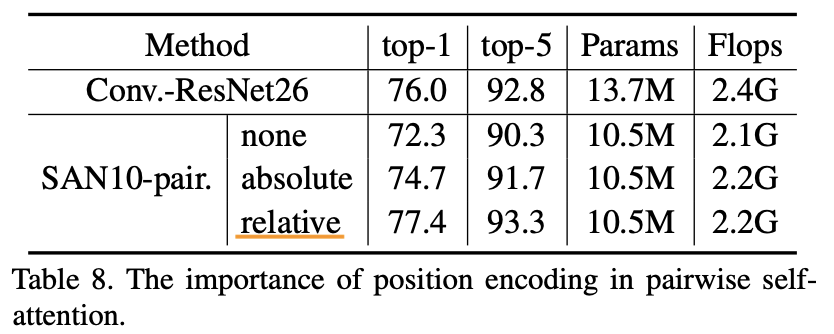
1.5.3.5 位置エンコーディングの有用性
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
最後に位置エンコーディングの有用性についてみていきます。「なし」、「絶対位置」、「相対位置」の3つで比較しています。「1.3.1.3 位置エンコーディング」で説明した位置エンコーディングは「相対位置」に該当します。上表の結果を見ると、位置情報で精度が上がること、絶対位置よりも相対位置の方が高い精度を示すことがわかります。位置情報強いですね。
1.5.4 ロバスト性
最後にSelf-Attentionを用いたモデルのロバスト性について見ていきます。ここでは2つ実験を行なっています。1つ目は回転や上下反転へのロバスト性、そして2つ目は敵対的攻撃へのロバスト性です。
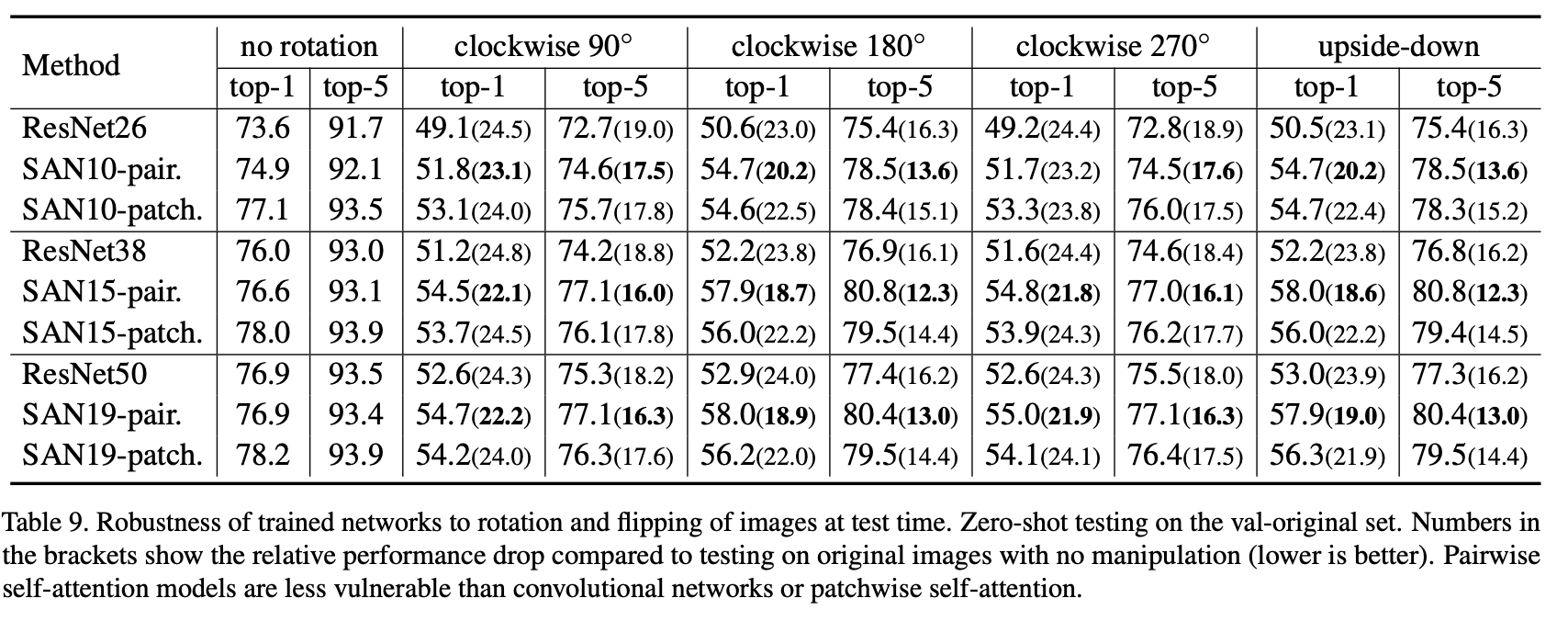
1.5.4.1 回転/上下反転へのロバスト性
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
ここでは回転角度90/180/270度と上下反転へのロバスト性を見ます。通常の学習データで学習させたモデルに対して、テスト画像に回転や上下反転を適用し性能評価した場合モデルはそういったノイズにも耐えうるのか、というのを見ています。結果は上表です。括弧内の数字は、回転などのノイズを加えていない場合からどれだけ性能が落ちたかを示しています(値は小さい方が良い)。結果から、ペアごとのSAが回転や上下反転には比較的耐えうるということがわかります。ただ、いずれも性能劣化は免れませんね。
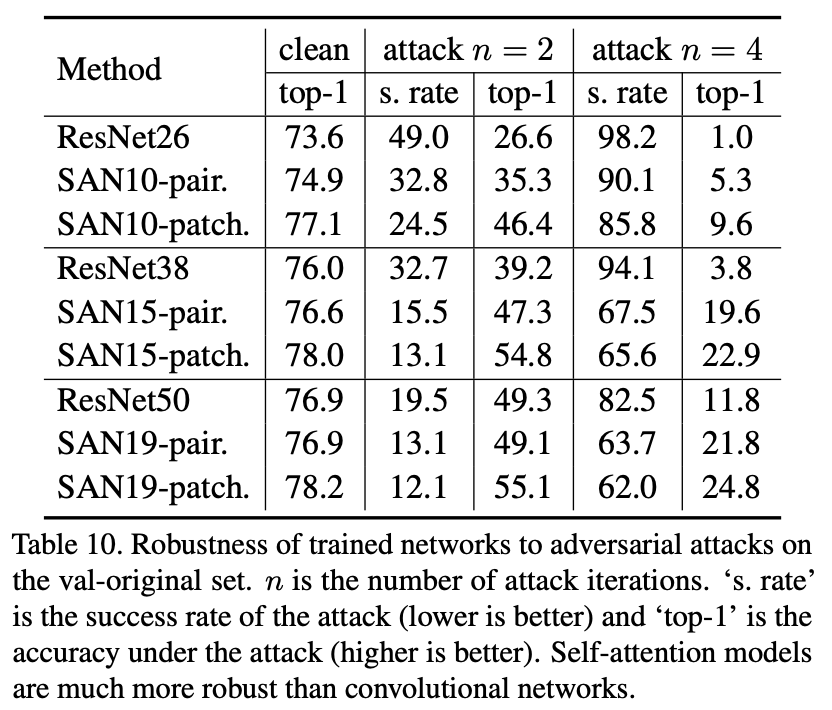
1.5.4.2 敵対的攻撃へのロバスト性
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
敵対的攻撃(=Adversarial Attack)へのロバスト性です。ニューラルネットが敵対的攻撃によって判断が揺らぎまくるのは有名ですが、ここではPGD攻撃[Madry, A.(ICLR'18)]を使用します。オプティマイザーのSGDはモデルの損失を小さくする方向に重みを調整するのに対して、PGDはモデルの損失が大きくなる方向に入力をイジくるという攻撃です。とても強いです。その強さは上表のResNetを見れば分かるかと思います。更新回数を4回($n=4$)に設定したPGDを施した場合、Top1精度はボコボコにやられています。
ただそれでもSANはResNetに比べるとPGDに大きく耐えていると言えますね。
1.6 結論
本論文では、空間およびチャネル方向にうまく対応することのできるベクトルAttentionとして「ペアごとのSA」と「パッチごとのSA」を提案し、SAのみを使った画像認識モデルの有用性を示しました。実験から言えることは次の3つです。
- 画像認識の発展には畳み込みではなく、Self-Attentionで代替ができる
- パッチごとのSAは特に強力で、さらなる発展が望める
- 内積のようなスカラーAttentionよりもベクトルAttentionの方が強力
2. 所感とまとめ
Self-Attentionがとうとう画像認識でも猛威を奮ってきそうですね。Self-Attention Networkは精度はさることながらロバスト性やパラメータ数/FLOPs数においても既存の畳み込みモデルを凌駕しているので、Self-Attentionは凄すぎます。これまでのテクニックは畳み込み用に作られてきたものが多いので、今度はSelf-Attention専用のテクニックが作られたらSAベースのネットワークはますますその真価を発揮することが期待できます。PyTorchであればこちらで実装してくれているので簡単に試してみてはいかがでしょうか!
3.参考
-
"Exploring Self-attention for Image Recognition" Zhao, H., Jia, J. Koltun, V. (CVPR'20)
原論文 -
Vladlen Koltun: Beyond convolutional networks (June 2020)
論文著者による説明動画。動画内前半部分が本論文の解説になっています。