Siamese Networkを理解してchainerで実装するまでの流れを書きたいと思います。
Siamese Networkとは、1クラスあたりの学習データが極端に少ないケース(これをone shot learningとかfew shot learningと言います)にでもうまく学習をしてくれるネットワークモデルです。
Siamese Networkは20年以上前に作られたものらしいのですが、近年のディープラーニングブームでSiamese NetworkにCNNやLSTMを組み込んだものが良い結果を出してきて、プチブームが起こっている気がします。(GANには遠く及びませんが)
このSiamese Networkに基づいた研究にNIPS2016で発表された”Matching Networks for One Shot Learning”(Oriol)があります。個人的にはこれを実装することが最終的な目標です。
その他にも関連する論文を載せておきます。
・Siamese Recurrent Architectures for Learning Sentence Similarity (Jonas and Aditya)リンク
SiameseNetwork+LSTMで文章間類似度の計測。
・Siamese Neural Networks for One-shot Image Recognition(Gregory)リンク
SiameseNetwork+CNNで画像の分類。
【背景〜導入】
Siamese Networkとは何か?を理解するために、以下の説明がとても役に立ちました。
[1]https://www.slideshare.net/NicholasMcClure1/siamese-networks
[2]https://hackernoon.com/one-shot-learning-with-siamese-networks-in-pytorch-8ddaab10340e
一例をあげて説明すると、
・データセット${(x_{0},x_{1},x_{2},...,x_{n}),(t_{0},t_{1},t_{2},...,t_{n})}$を用意する。($x$がデータ、$t$がラベル)
・適当に2つのデータ$x_{a}$,$x_{b}$をとってきて、$t_{a}=t_{b}$ならば$t_{ab}=1$、それ以外ならば$t_{ab}=0$とする。
・2つのデータ点$x_{a}$,$x_{b}$を、同じ関数(ここでは重みを共有したニューラルネットワーク)に入れる。
・2つ出力$y_{a}$,$y_{b}$が得られる。
・2点間の距離を測る関数(例えばマンハッタン距離関数)$D$を用いて、$D(y_{a},y_{b})$を出力する。
・$MSE(D(y_{a},y_{b}),t_{ab})$を誤差としてバックプロバゲーションをする。
という流れになります。
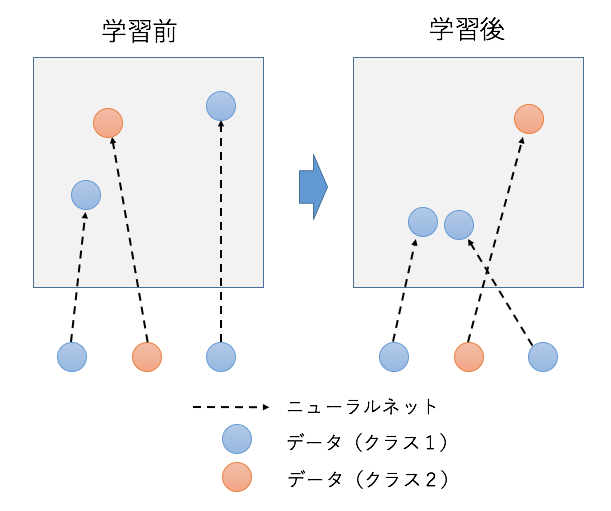
これは、同じクラス同士のデータを近くに、違うクラス同士のデータを遠くに写像するようなニューラルネットワークを求めていると解釈することができます。そういった点で、Siamese Networkは計量学習ともいえそうです。
ちなみに、[2]の記事にあるようにContrastive Loss functionを使う場合は、
「$t_{a}=t_{b}$ならば$t_{ab}=1$、それ以外ならば$t_{ab}=0$とする。」の部分が逆になります。
次回は実装部分について書いていこうかと思います。