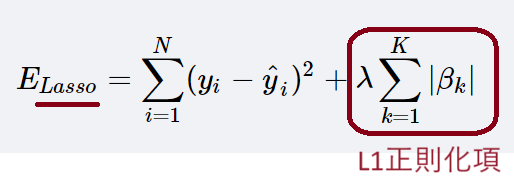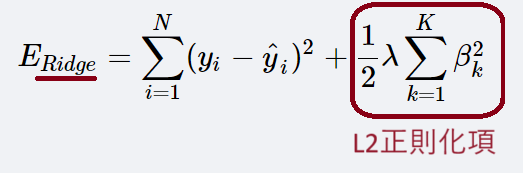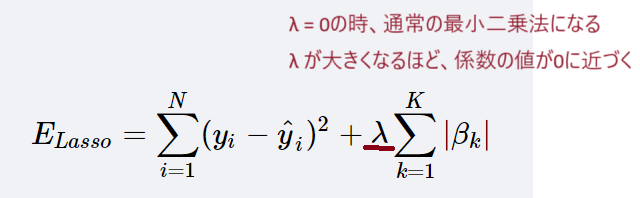リッジ回帰とラッソ回帰はどう使い分けるのだろう？
調べた際の勉強メモ。
最初はリッジ回帰とラッソ回帰って何？という基本的な話です。
不要な方はスキップ。
続いて、使い分けを扱います。
リッジ回帰とラッソ回帰とは何か
- 回帰モデルを作る時に使う手法。
- 回帰係数を推定する際、損失関数を最小化するように係数を決める。
その時に過学習を防ぐための工夫がこらされている。 - どんな手法？ー損失関数に正則化項を仕込む。
その正則化項には2種類ある
L1正則化項とL2正則化項である。
L1正則化項は、回帰係数の絶対値の和
L2正則化項は、回帰係数の自乗の和
λ(ラムダと読む)はコストパラメータ。
つまりλが大きくなる
→回帰係数は0に近づく
→バリアンスが小さくなっていく
→過学習を回避しやすくなる
↓ラッソ回帰のみ記載だがリッジ回帰も同様
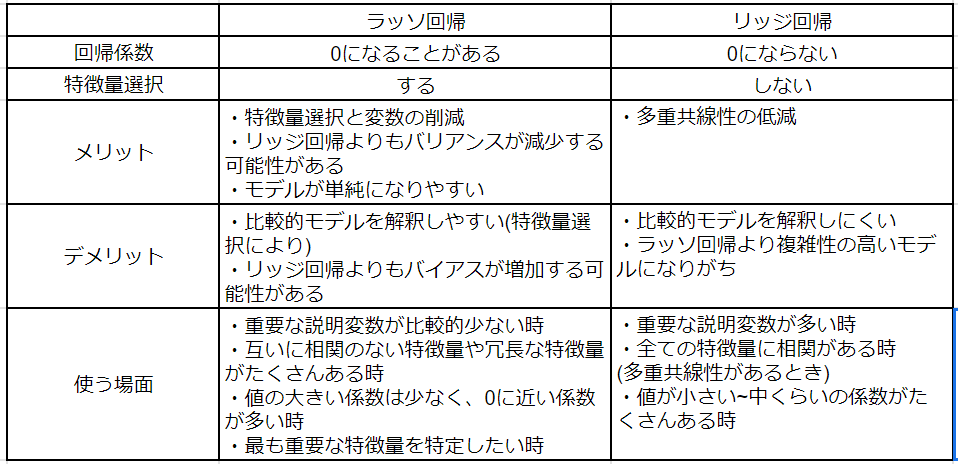
じゃあどうリッジ回帰とラッソ回帰はどう使い分けるの？
使い分けは以下のとおり
補足1:ラッソ回帰は係数を0にすることがあるのに、リッジ回帰で係数が0にならないのはなぜ？
と思った方は、最後の参考サイトにあるヨビノリさんの動画をご参照ください。図形で解説しており納得しやすい。
補足2:多重共線性のある場合にリッジ回帰が有効？
これは、以下サイトによると機械学習を用いて予測を行うという目的の場合のみかもしれない。
すなわち、統計学の文脈では有効とは限らない。
詳細はこちらのサイトを参照ください。
余談：記憶の助け
ラッソ(ら)とL1(わん)はaの音で韻を踏める。
リッジは自乗(じ)なので、じが共通している。
それで無理やり紐づけて記憶する。
参考サイト
Ridge Regression vs Lasso Regression
Lasso vs Ridge vs Elastic Net | ML