[vDSP][Signal Processing] Audio Analysis 5 FFT
This article is also readable in
http://sourcecodedust.blogspot.ch/2015/06/vdspsignal-processing-audio-analysis.html
Here I introduce how to implement Fast Fourier Transform by using vDSP (Acceleration.framework) with C code.
Process
- Define FFT setup
- Extract audio data of FFT frame size
- Windowing the audio data obtained in the process 2
- Convert audio data to DSPSplitComplex types.
- Execute FFT
- Do scaling
In the fourth process, we find a data type DSPSplitComplex that can store both real and imaginary numbers. The structure of the data type of DSPSplitComplex is shown as follows,
typedef struct DSPSplitComplex {
float *realp;
float *imagp;
} DSPSplitComplex;
DSPSplitComplex is used for float type of real and imaginary numbers. On the other hand, the double data type is treated by DSPDoubleSplitComplex .
Window
There are several vDSP functions for making window functions.
Here I introduce some of the most popular window functions.
hanning
extern void vDSP_hann_window(
float *__vDSP_C,
vDSP_Length __vDSP_N,
int __vDSP_Flag)
__OSX_AVAILABLE_STARTING(__MAC_10_4, __IPHONE_4_0);
hamming
extern void vDSP_hamm_window(
float *__vDSP_C,
vDSP_Length __vDSP_N,
int __vDSP_Flag)
__OSX_AVAILABLE_STARTING(__MAC_10_4, __IPHONE_4_0);
blackman
extern void vDSP_blkman_window(
float *__vDSP_C,
vDSP_Length __vDSP_N,
int __vDSP_Flag)
__OSX_AVAILABLE_STARTING(__MAC_10_4, __IPHONE_4_0);
etc.
Thoese of all functions introduced above are for float data type and are adopted by adding D at the end of function name for double data type.
For example, hanning winwodw can be written as below,
extern void vDSP_hann_windowD(
double *__vDSP_C,
vDSP_Length __vDSP_N,
int __vDSP_Flag)
__OSX_AVAILABLE_STARTING(__MAC_10_4, __IPHONE_4_0);
Now, I show you the main function which handles FFT analysis.
main()
# define PAI 3.14159265358979323846264338 // PAI
# define SAMPLE_RATE 44100 //sampling rate
# define LENGTH 4 // 4 seconds
# define AMPLITUDE 1.0// 16bit
# define FREQUENCY 440 // frequency Hz
# define FFTSIZE 2048
int main(int argc, const char * argv[])
{
//Libsndfile
SNDFILE *fp;
SF_INFO sfinfo;
float *buffer;
buffer = malloc(FFTSIZE*sizeof(float));
memset(&sfinfo,0,sizeof(sfinfo));
sfinfo.samplerate = SAMPLE_RATE;
sfinfo.frames = SAMPLE_RATE*FFTSIZE;
sfinfo.channels = 1;
sfinfo.format = (SF_FORMAT_WAV | SF_FORMAT_PCM_16);
if(!(fp = sf_open("Sawtooth.wav", SFM_WRITE, &sfinfo))){
printf("Error : Could not open output file .\n");
return 1;
}
int i;
for(i=0;i<FFTSIZE;i++){
buffer[i] = AMPLITUDE * sin((float)FREQUENCY / SAMPLE_RATE * 2 * PAI * i);
}
int ffthalfsize = FFTSIZE/2;
DSPSplitComplex splitComplex;
//allocate complex (fft half size)
splitComplex.realp = malloc(sizeof(float)*ffthalfsize);
splitComplex.imagp = malloc(sizeof(float)*ffthalfsize);
float *magnitude = malloc(sizeof(float)*ffthalfsize);
FFT(buffer,&splitComplex);
vDSP_zvabs(&splitComplex, 1, magnitude, 1, ffthalfsize);
float freq_bins = (float)SAMPLE_RATE/FFTSIZE;
for(i=0;i<ffthalfsize;i++){
printf("%0.2f Hz: magnitude = %f\n",i*freq_bins,magnitude[i]);
}
FFT_free(&splitComplex);
if(sf_write_float(fp, buffer,sfinfo.channels *FFTSIZE)!= sfinfo.channels *FFTSIZE)
puts(sf_strerror (fp));
free(buffer);
sf_close(fp);
return 0;
}
Here we focus on the place after sin wave is generated.
int ffthalfsize = FFTSIZE/2;
DSPSplitComplex splitComplex;
//allocate complex (fft half size)
splitComplex.realp = malloc(sizeof(float)*ffthalfsize);
splitComplex.imagp = malloc(sizeof(float)*ffthalfsize);
float *magnitude = malloc(sizeof(float)*ffthalfsize);
FFT(buffer,&splitComplex);
vDSP_zvabs(&splitComplex, 1, magnitude, 1, ffthalfsize);
float freq_bins = (float)SAMPLE_RATE/FFTSIZE;
for(i=0;i<ffthalfsize;i++)
printf("%0.2f Hz: magnitude = %f\n",i*freq_bins,magnitude[i]);
FFT_free(&splitComplex);
In the soruce code, the FFT frame size = 2048.
Make Half FFT frame size.
int ffthalfsize = FFTSIZE/2;
Subsequently, declare DSPSplitComplex data and allocate memory spaces for both real and imaginary numbers. The size of both scolars are half of fft frame size.
splitComplex.realp = malloc(sizeof(float)*ffthalfsize);
splitComplex.imagp = malloc(sizeof(float)*ffthalfsize);
Next, allocate memory space for storing spectral magnitude. The size of the space is half fft frame size.
float *magnitude = malloc(sizeof(float)*ffthalfsize);
Finally, we execute FFT.
I made FFT() user function whose instruction is shown after this sub-section.
FFT() takes pointer of buffer and splitComplex as its arguments.
FFT(buffer,&splitComplex);
When FFT() is executed, the result is stored in real and imaginary spaces of splitComplex.
We can obtain spectral magnitude by calcurating the power of these numbers.
vDSP_zvabs(&splitComplex, 1, magnitude, 1, ffthalfsize);
vDSP_zvabs() calculates sqrt(real * real + img * img) and stores the result in magnitude.
extern void vDSP_zvabs(
const DSPSplitComplex *__vDSP_A,
vDSP_Stride __vDSP_IA,
float *__vDSP_C,
vDSP_Stride __vDSP_IC,
vDSP_Length __vDSP_N)
__OSX_AVAILABLE_STARTING(__MAC_10_4, __IPHONE_4_0);
Stride is 1.0.
vDSP_Length represents the data length of the calculation and so that it should be ffthalfsize.
Calculate which FFT bin corresponds what frequency.
float freq_bins = (float)SAMPLE_RATE/FFTSIZE;
Output the result.
for(i=0;i<ffthalfsize;i++)
printf("%0.2f Hz: magnitude = %f\n",i*freq_bins,magnitude[i]);
Here some of the result.
0.00 Hz: magnitude = 0.000018
21.53 Hz: magnitude = 0.000018
43.07 Hz: magnitude = 0.000019
64.60 Hz: magnitude = 0.000020
86.13 Hz: magnitude = 0.000023
107.67 Hz: magnitude = 0.000026
129.20 Hz: magnitude = 0.000030
150.73 Hz: magnitude = 0.000036
172.27 Hz: magnitude = 0.000044
193.80 Hz: magnitude = 0.000055
215.33 Hz: magnitude = 0.000072
236.87 Hz: magnitude = 0.000096
258.40 Hz: magnitude = 0.000134
279.93 Hz: magnitude = 0.000195
301.46 Hz: magnitude = 0.000301
323.00 Hz: magnitude = 0.000504
344.53 Hz: magnitude = 0.000943
366.06 Hz: magnitude = 0.002103
387.60 Hz: magnitude = 0.006500
409.13 Hz: magnitude = 0.051471
430.66 Hz: magnitude = 0.221126
452.20 Hz: magnitude = 0.202370
473.73 Hz: magnitude = 0.034186
495.26 Hz: magnitude = 0.005429
516.80 Hz: magnitude = 0.001862
538.33 Hz: magnitude = 0.000858
559.86 Hz: magnitude = 0.000466
581.40 Hz: magnitude = 0.000281
602.93 Hz: magnitude = 0.000182
624.46 Hz: magnitude = 0.000125
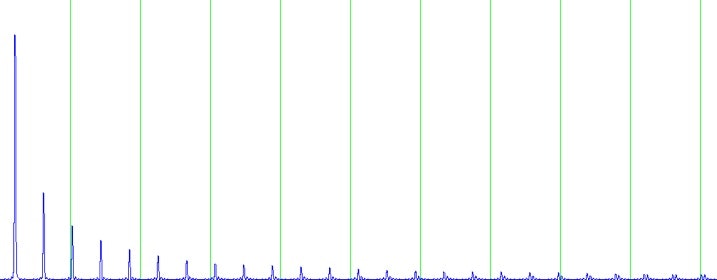
We used a sin wave of 440Hz for the FFT analysis.
In the result, we can find that the bins that have the most highest magnitude are around 430Hz and 452Hz and which suggests the highest magnitude exists between these two bins(which is nearby 440Hz).
The figure shows the spectrogram of the result.
FFT()
This section instructs the user-function "FFT()"
The code of FFT() as follows,
void FFT(float *wavedata, DSPSplitComplex *splitComplex)
{
int ffthalfsize = FFTSIZE/2;
vDSP_Length log2n = log2(FFTSIZE);
//setup fft
FFTSetup fftsetup = vDSP_create_fftsetup(log2n, kFFTRadix2);
//make window (fft size)
float *window = malloc(sizeof(float)*FFTSIZE);
//hanning window
vDSP_hann_window(window, FFTSIZE, 0);
//windowing
vDSP_vmul(wavedata, 1, window, 1, wavedata, 1, FFTSIZE);
//transform to complex
vDSP_ctoz( ( COMPLEX * )wavedata, 2, splitComplex, 1, ffthalfsize );
//FFT forward
vDSP_fft_zrip(fftsetup, splitComplex, 1, log2n, FFT_FORWARD);
//scaling
float scale = 1.0/(FFTSIZE*2);
vDSP_vsmul(splitComplex->realp, 1, &scale, splitComplex->realp, 1, ffthalfsize);
vDSP_vsmul(splitComplex->imagp, 1, &scale, splitComplex->imagp, 1, ffthalfsize);
//free
vDSP_destroy_fftsetup(fftsetup);
free(window);
}
FFT() takes two argments, 1) float type of audio data buffer whose length is fft size, and DSPSplitComplex型 data in which the results are stored as real and imaginary.
make Half FFT size
int ffthalfsize = FFTSIZE/2;
vDSP_Length log2n = log2(FFTSIZE);
Define setup of FFT for vDSP
//setup fft
FFTSetup fftsetup = vDSP_create_fftsetup(log2n, kFFTRadix2);
The first argument is natural logarithm of FFT size, adn the second argument is the mode of FFT, in thise case I setup kFFTRadix2 = 0
Subsequently, generating a window functon. In thise case, I use hanning window.
float *window = malloc(sizeof(float)*FFTSIZE);
vDSP_hann_window(window, FFTSIZE, 0);
the plot of a hanning window.
multiply the generated hanning window with the audio data buffer.
vDSP_vmul(wavedata, 1, window, 1, wavedata, 1, FFTSIZE);
The plot of the original audio data buffer
The plot of the windowed audio data buffer
Finally we can do FFT process!
Now we have to convert the windowed audio data buffer to COMPLEX data tyoes with which process is a bit tricky and very important to obtain the accurate result.
we use following function.
vDSP_ctoz( ( COMPLEX * )wavedata, 2, splitComplex, 1, ffthalfsize );
We have to pay attention about the Stride arguments as they are set 2 for Complex wavedata and 1 for splitcomplex. It is because of that, audio data buffer (wavedata) has FFT size length and on the other hand, the length pof splitComplex is only half-fftsize. Thefore we need to set double number of splicomplex stride to the (Complex *)wavedata.
However, the process data amount should be ffthaldsize as it is set as 5th argument.
Now audio data buffer is converted to splitComplex. We can simply FFT splitComplex.
vDSP_fft_zrip(fftsetup, splitComplex, 1, log2n, FFT_FORWARD);
Forward FFT is done by FFT_FORWARD as 5th argumtne and inverse FFT is done by FFT_INVERSE
We must not forget to scale the obtained splitComplex variables.
This process is important to get actual magnitude of the analyzed audio data and for the case you want to do inverse FFT afterwards.
float scale = 1.0/(FFTSIZE*2);
vDSP_vsmul(splitComplex->realp, 1, &scale, splitComplex->realp, 1, ffthalfsize);
vDSP_vsmul(splitComplex->imagp, 1, &scale, splitComplex->imagp, 1, ffthalfsize);
Free all unneccesary data.
//free
vDSP_destroy_fftsetup(fftsetup);
free(window);
FFT_free()
also free splitComplex data
void FFT_free(DSPSplitComplex *splitComplex)
{
free(splitComplex->realp);
free(splitComplex->imagp);
}
Square wave
The Spectrogram of the square wave analyzed by above program.