AtCoder緑になるまでに勉強した基本的なアルゴリズムやデータ構造まとめ

先日開催されました東京海上日動プログラミングコンテスト 2020 で緑レートになることができました。

　中には初回参加で緑になってしまう人もいるようですが、自分の場合そう順調にいくはずもなく、ここまで来るのに結構自己学習を重ねてきました。初参加したコンテストはアルゴリズムやデータ構造などは No 勉強、過去問も大体 10 門程度を解いただけでの参加ということもあり、灰色 diff でした。そこからコツコツ勉強を重ね、10 回目のコンテスト参加でようやく緑になれました。このブログでは今までに自身が学習したアルゴリズムやデータ構造を備忘録の意味も含めまとめ＆Python での実装をして行きたいと思います。

もしこの記事がお役にたったら LGTM いただけると幸いです。

自身のスペック

• 大学、大学院は理系だが、情報系ではない。
• 数学は昔から苦手ではないが、決して得意でもない。
• プログラミング歴は 1 年半程度
• 普段の業務では Python を使っており、AtCoder も Python で参戦
• C++はシンプルなコードなら読める
• 機械学習も勉強していて、KaggleExpert 程度

学習したアルゴリズム&データ構造

bit 全探索

概要

要は全探索なのですが、、、一応実装の仕方とか初めは知らなかったため書き記しておきます。bit 全探索は完結に言うと、与えられた全パターンが bit(0 or 1)の組み合わせで表現できる場合に、それらの組み合わせを全て列挙していくアルゴリズムです。
　例えば、$N$人の人間がいる際に、それぞれが男性であるか女性であるかの組み合わせの総数は
$$ O(2^N) = N[bit] $$
となります。指数関数的に計算量が増大していくので、制約も結構厳し目です。なので AtCoder で出題される場合、比較的現実にありそうなシチュエーションの問題が多い気がします。

実装

<<は左シフト演算子になるので、下記の場合、$1$を$3$だけ左シフトする（$2^3=8$）回ループになります。
　>>は右シフト演算子になります。下記の場合例えばi=5（二進数で101）とすると、j=0, 1, 2となるにつれ、それぞれi>>j=101, i>>j=10, i>>j=1となります。これと$1$の論理積をとる（つまり 1 の位が 0 か 1 を判定する）ことになります。出力値に注目すると、全てのパターンが網羅されていることが分かります。
　尚、通常の bit 全探索の実装を少し変えて、(0, 1, 2)の 3 パターン（$3^N$）の組み合わせを列挙していくなどの応用も可能です。

N = 3

for i in range(1<<N):
    cond = [0]*N
    for j in range(N):
        if 1&(i>>j):
            cond[j] = 1
    print(cond)

"""
[out]
[0, 0, 0]
[1, 0, 0]
[0, 1, 0]
[1, 1, 0]
[0, 0, 1]
[1, 0, 1]
[0, 1, 1]
[1, 1, 1]
"""

（2020/06/20 追記）
@39yatabis さんのコメントより Python のitertoolsを使用して、以下の様にスマートに書く実装もある様です。この方が分かりやすい気がします。

from itertools import product

N = 3

for p in product((0, 1), repeat=N):
    print(p)

二分探索

概要

ある数列がソートされている場合に使える探索法です。例えば$N$個の数字が並んだ数列からある数を探索する場合、線形探索だと最悪ケースの場合、$O(N)$の計算量が必要ですが、二分探索の場合、$O(logN)$で探索可能です。

二分探索 - Wikipedia

実装

Python にはデフォルトでライブラリが用意されているので、それをそのまま使うのが簡単です。

# return index
from bisect import bisect_right

def search(t, i):
    """
    t: list 探索元の数列
    i: int 探索する値
    """
    ix = bisect_right(t, i)
    if t[ix-1] != i:
        return False
    return True

t = [1,3,5,6,7,10]
i = 7

print(search(t, i))  # True

幅優先探索（BFS）

概要

迷路やグラフの探索でよく使われます。こちらのブログが非常に分かりやすいです。

BFS (幅優先探索) 超入門！ 〜 キューを鮮やかに使いこなす 〜

上記ブログのまんまですが、BFS ではキューを使います。キューは行列に並ぶ人の列を想像すると分かりやすいです。先に並んだ人から抜けていく、いわゆる先入れ先出し（First In First Out : FIFO）型の記憶装置になります。一方、これとは逆に後入れ先出し（Last In First Out : LIFO）型の記憶装置をスタックといいます。

実装

AtCoder のこちらの問題が典型かなと思います。問題名からして、どのようなアルゴリズムを使うのか想像できてしまいます。

AtCoder ABC007 C - 幅優先探索

from collections import deque

R, C = map(int, input().split())
sy, sx = map(int, input().split())
gy, gx = map(int, input().split())
sy, sx, gy, gx = sy-1, sx-1, gy-1, gx-1
c = [[c for c in input()] for _ in range(R)]
visited = [[-1]*C for _ in range(R)]


def bfs(sy,sx,gy,gx,c,visited):
    visited[sy][sx] = 0
    Q = deque([])
    Q.append([sx, sy])
    while Q:
        y,x = Q.popleft()

        if [y, x] == [gy, gx]:
            return visited[y][x]

        for i, j in [(0, 1), (1, 0), (-1, 0), (0, -1)]:
            if c[y+i][x+j] == '.' and visited[y+i][x+j] == -1:
                # 探索可能かつ未探索の場合
                visited[y+i][x+j] = visited[y][x]+1
                Q.append([y+i,x+j])


print(bfs(sy, sx, gy, gx, c, visited))

visitedはスタート位置からの距離を格納していく二次元配列です。未探索の座標に関しては-1が立っています。cは実際に探索していく迷路で、障害物などの情報も持ちます。関数内で定義されるQがキューに当たりますが、こちらに次回探索予定の座標をドンドン enqueue（追加）していきます。そして先に追加された座標からドンドン dequeue（削除）していきます（探索していく）。そしてゴールに到着した時点でその距離（要は最短距離）を返します。

深さ優先探索（DFS）

概要

BFS との対比で紹介されることの多い探索方法です。BFS では探索開始元からの距離が近い方からしらみ潰しに探索していくのに対し、DFS は一つのルートについて行き止まりまで一気に探索するアルゴリズムになります。

実装

DFS の実装はスタックを使う方法、もしくは再帰関数を用いる方法などがあります。下記の問題では再帰関数を用いた方法で実装しています。

AtCoder ABC138 D - Ki

N, Q = map(int, input().split())
tree = [[] for _ in range(N)]

for _ in range(N-1):
    a, b = map(int, input().split())
    tree[a-1].append(b-1)
    tree[b-1].append(a-1)

X = [0]*N
for _ in range(Q):
    p, x = map(int, input().split())
    X[p-1] += x

ans = [0]*N

def dfs(u, parent=None):
    """
    u: 子ノード
    parent: 親ノード
    """
    ans[u] = ans[parent] + X[u]
    for v in tree[u]:
        if v != parent:
            dfs(v, u)

dfs(0, 0)
print(' '.join([str(i) for i in ans]))

ある木のノードに $+x$ の加点が会った際に、その配下の子孫ノード全てに $+x$ の加点をしていく問題です。上記のコードでは、再帰処理を行うことで、次々に配下ノードの探索を行っています。

しゃくとり法

概要

最早概要はこの方のブログを見るのが早いです。

しゃくとり法 (尺取り法) の解説と、それを用いる問題のまとめ

先ほどから何度も出てるのですが、この方のブログは本当に丁寧で分かりやすいので、競プロ云々に関わらずチェックする価値があると思います。

実装

AtCoder ABC138 C - 単調増加

$N$個の数列から、条件に合致した部分数列のパターン数を求める問題です。本当に愚直に計算すると始点と終点の全パターンを列挙しなくてはいけないため、$O(N^2)$と莫大な計算量になってしまいます。しかし、しゃくとり法を使うことで、$O(N)$で計算可能となります。

N = int(input())
A = list(map(int, input().split()))
A = A + [-1]

def sum_return(n):
    return n*(n+1)//2

cnt = 0
ans = 0
pre = -1

for i in range(N+1):
    if A[i] > pre:
        cnt += 1
    else:
        ans += sum_return(cnt)
        cnt = 1
    pre = A[i]

print(ans)

条件をクリアしている間はiをインクリメントしていくだけで、特にパターン数の数え上げは行いません。しかし、条件に合致しなかった場合、sum_return関数でそれまでの条件に合致している数列の中で幾つの部分数列が生成できるのか、その数を返している形になります。

いもす法

概要

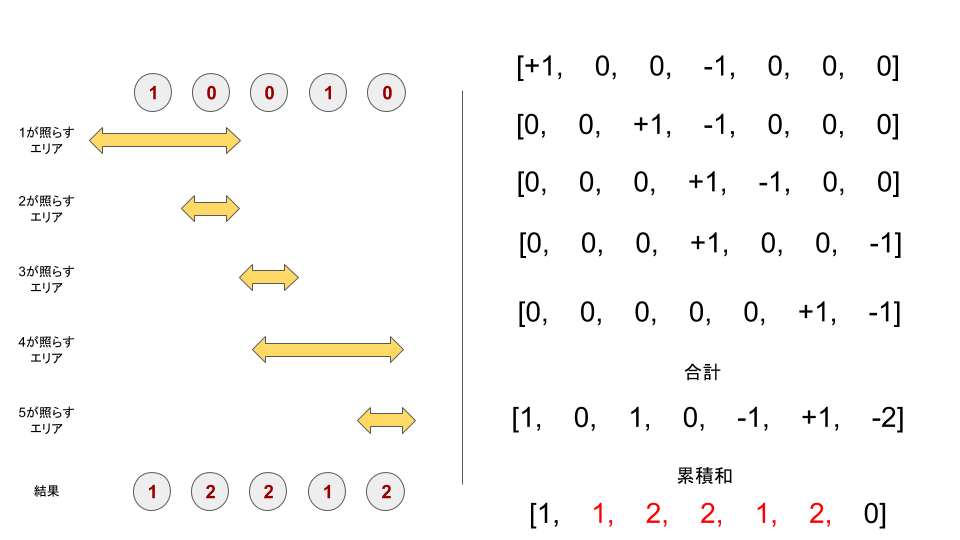
AtCoder 東京海上日動 プログラミングコンテスト 2020 C - Lamps

上記問題のイメージを作ってみました。

左側の矢印区間を足し合わせていく問題ですが、上手く累積和を使うことで$O(N)$で計算が可能です。数の単純な足し合わせ以外でも、オセロの裏表を交互にひっくり返していくような問題にも使えます。

実装

最近、覚えたアルゴリズムで実際に解いたことのある問題が 1 問しかなかったため、少し典型問題とは言いにくいかも知れませんが、上記問題は以下のように実装できます。

import numpy as np
from numba import jit
N, K = map(int, input().split())
A = np.array(list(map(int, input().split())), dtype=np.int64)

# 高速化
@jit
def imo(a, n):
    imos = np.zeros(n+1, dtype=np.int64)
    for i in range(n):
        imos[max(0, i-a[i])] += 1
        imos[min(n, i+a[i])+1] -= 1

    # 累積和はnumpyの方が高速
    immo = np.zeros(n+1, dtype=np.int64)
    immo = np.cumsum(imos)

    return immo[:n]


for _ in range(min(K, 41)):
    A = imo(A, N)

print(*A)

numbaライブラリやnumpyを使った高速化。41 での計算打ち止め（詳細は公式解説が分かりやすいです。）など、結構工夫をしています。

ダイクストラ

概要

グラフの距離を高速に求めるアルゴリズムです。自分は初めてダイクストラを知った時、人間が頭の中でイメージする最短距離の求め方（例えば電車の乗り継ぎ）と非常に近い考えだなと思いました。なので結構印象に残っているアルゴリズムです。ある地点からある地点の最短距離を求める際に、どの地点を経由していけば最も効率的に進めるかを逐次更新していく形になります。

実装

AtCoder ABC016 C - 友達の友達

友達関係を無向グラフとして、距離が 2 同士の関係がいくつあるかを求めています。

n, m = map(int, input().split())
friend = [[100 for _ in range(n)] for _ in range(n)]

for _ in range(m):
    a, b = map(int, input().split())
    a, b = a-1, b-1
    friend[a][b] = 1
    friend[b][a] = 1

for i in range(n):
    friend[i][i] = 0

for k in range(n):
    for i in range(n):
        for j in range(n):
            friend[i][j] = min(friend[i][j], friend[i][k]+friend[k][j])
            # ダイクストラ法
            # iからjに直接行くよりもkを経由した方が近い場合、iとjの距離を更新

for m in range(n):
    print(friend[m].count(2))
    # 最終的に距離が2の関係がいくつあるかを出力

尚、ダイクストラは優先度付きキューを使うことで、その計算量を削減できます。

貪欲法

概要

wikipedia には以下の様に書いていました。

以下引用（https://ja.wikipedia.org/wiki/%E8%B2%AA%E6%AC%B2%E6%B3%95）
貪欲法は局所探索法と並んで近似アルゴリズムの最も基本的な考え方の一つである。 このアルゴリズムは問題の要素を複数の部分問題に分割し、それぞれを独立に評価を行い、評価値の高い順に取り込んでいくことで解を得るという方法である。

常に最善の手が決まっていて、それらを独立に求めていくことにより、最終的な最適解を求めていくといったアルゴリズムです。闇雲に探索をしないといった感じで考え方は結構シンプル。ただ与えられた問題が貪欲法で求められるかどうかを判断するのは結構難しい気がしてます。

実装

貪欲法についても、自身があまり解いてきた問題が少ないため、ちょっと典型問題とは言えないかもしれませんが、一応下記問題がそれにあたります。本番ではすごく難しく感じて解けなかったのですが、解説を見てなるほどと思いました。（ただ実装自体はできたのですが、本当にそれで OK な深い意味での理解は正直できていません。）

AtCoder ABC161 E - Yutori

問題の概要は以下の通りです。

概要

• $N$日間のうち、$K$日間働く。
• ある日働いたら、その直後の$C$日間は働かない。
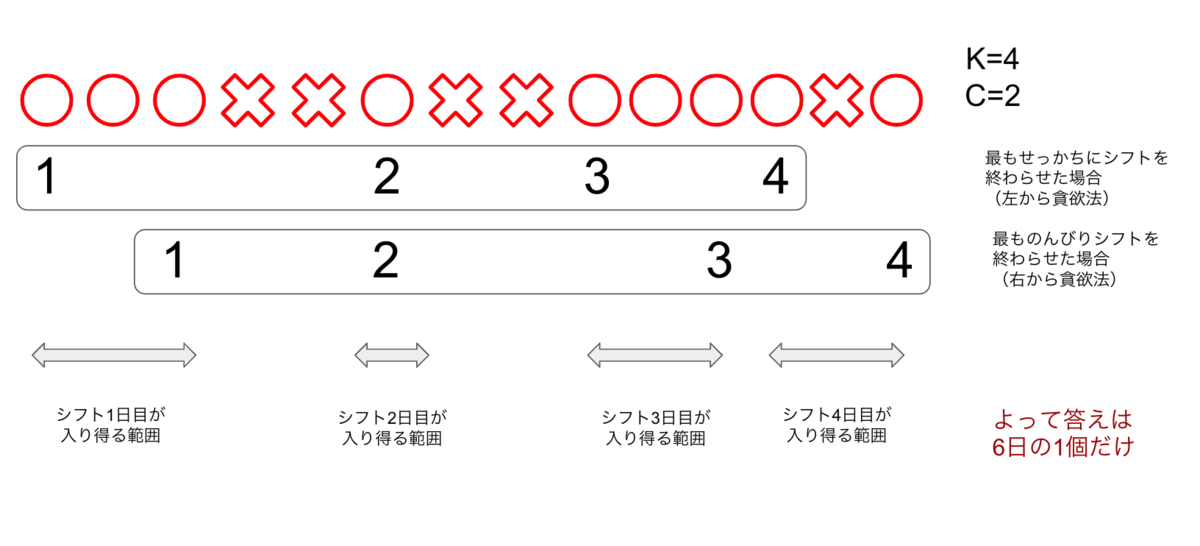
• $S$のi文字目が x の時は働かない。
• この時、必ずシフトに入る日を全て列挙せよ。

解法ですが、最も早くシフトを終了させる様に行動した場合（左から貪欲）と、最も遅くシフトを終わらせた場合（右から貪欲）の行動パターンを列挙します。こうしてシフト各日における可能な範囲を求めていく形になります。

以下は$N=14, K=4, C=2$の時の例です。

N, K, C = map(int, input().split())
S = list(input())
rS = S[::-1]
lcnt, rcnt = 0, 0
left, right = [0]*N, [0]*N
llimit, rlimit = -1, -1

for i in range(N):
    # 左から貪欲
    # llimit (数字がカウントされた日+C日)以降
    # 上記かつ、シフトに入れる日 ('o')であればシフトに入る。
    if S[i] == 'o' and llimit<i:
        lcnt += 1
        left[i] = lcnt
        llimit = i + C

    # 右から貪欲
    if rS[i] == 'o' and rlimit<i:
        rcnt += 1
        right[-(i + 1)] = K + 1 - rcnt
        rlimit = i + C

#print(left)
#print(right)

# leftとrightで同じ数字が入っている日にちを出力
for i in range(N):
    if left[i]==right[i] and left[i]>0:
        print(i + 1)

動的計画法（DP）

概要

自分が出てきたコンテストのイメージですが、DP は結構頻出な気がしてます。ただ、問題設定が複雑になってくると、実装が重くなるイメージがあり、一筋縄では行かない問題も多い気がしてます。DP の定義ですが wikipedia には以下の様に書いていました。

以下引用（https://ja.wikipedia.org/wiki/%E5%8B%95%E7%9A%84%E8%A8%88%E7%94%BB%E6%B3%95）
効率のよいアルゴリズムの設計技法として知られる代表的な構造の一つである。対象となる問題を帰納的に解く場合にくり返し出現する小さな問題例について、解を表に記録し表を埋めていく形で計算をすすめ、冗長な計算をはぶくアルゴリズムのことをいう。特定のアルゴリズムを指すのではなく、上記のような手法を使うアルゴリズムの総称である。

帰納的というワードがポイントで、一発で最適解が求まらない様な問題に対して、独立したそれぞれの問題で最適解を求めていきつつ、最終的な最適解を導き出すアルゴリズムになります。定義だけ見ると貪欲法と似ていますが、異なる点として貪欲法と異なり保持する状態は常に一定ではなく、一度選択した要素を更新しながら最適解を導いて行きます。

実装

AtCoder ABC129 C - Typical Stairs

壊れている段を避けながら階段を登っていくとした時、頂点までいくルートの数を求める問題です。

N, M = map(int, input().split())
A = set([int(input()) for _ in range(M)])
mod = 10**9+7

step = [0] * (N+1)
step[0] = 1
step[1] = 1

for i in range(N+1):
    if i==0 or i==1:
        if i in A:
            step[i] = 0
    else:
        step[i] = step[i-1]+step[i-2]
        if i in A:
            step[i] = 0
        step[i] %= mod

print(step[-1])

step配列に、その段へいく方法が何通りあるかを格納していきます。なので壊れている段は勿論0になります。パターン数の求め方は以下の様に求めることが可能です。

$$ stepi = step{i-1} + step_{i-2} $$

今更ですが、自分のコードを見て、if i in Aの部分で無駄に処理時間かかってる気がするので、ここは初めから配列を生成しておき、その配列に予め段の故障情報（bool 値）を格納しておいた方が早そうな気がします。一応上のコードでもこの問題は AC でした。

優先度付きキュー

概要

まだ自身としても使った場面が少ないデータ構造ですが、一応概要だけは学習したので記載します。通常の配列だと追加や削除は早いものの、狙った値を取得する動作（例えば最大値）はソートでもしない限りどうしても遅くなってしまいます。また一度ソートしたとしても、次々に値が追加されていくたびにソートしていてはどうしても処理時間がかかってします。その様な場合に使えるデータ構造です。その概要は以下のサイトがまとまっていて分かりやすいかと思います。データの格納方法を工夫することで処理を高速化しています。

優先度付き待ち行列

実装

AtCoder ABC141 D - Powerful Discount Tickets

Python では単純な機能だけなら、特に自作する必要もなく簡単に実装できます。下記のコードですが、問題で求めたいのは最大値です。デフォルトで返ってくるのが最小値のため、あるあるな手法ですが、$-1$倍することで大小関係を逆転させています。

from heapq import (
    heapify,  # 優先度付きキューの生成
    heappop,
    heappush,
    heappushpop,
    heapreplace
    )

N, M = map(int, input().split())

# 最小値が返ってくるので-1倍する
A = [-i for i in map(int,input().split())]
heapify(A)

for _ in range(M):
    s = -heappop(A)
    s //= 2
    heappush(A, -s)

print(-sum(A))

UnionFindTree

概要

グラフ問題が出題された際、グルーピング処理をしていく、どのグループに属しているか判定するなどの処理が必要な場合に使われることの多いデータ構造です。

競プロ覚書：Union-Find まとめ

実装

Python での実装ですが、自分は以下のクラスを VSCode のスニペットとして用意しています。実際自分で書いたわけではなく、色んなサイト回ってきて所々コピペしてきたものです。勿論はじめは 1 行 1 行解釈しながらやりましたが、コンテストの場合、事前準備をしてすぐに出せた方が良いかなと思います。

AtCoder ARC032 B - 道路工事

class UnionFind:
    def __init__(self, n):
        self.par = list(range(n)) #親
        self.rank = [0] * n #根の深さ

    # xの属する根を求める
    def find(self, x):
        if self.par[x] == x:
            return x
        else:
            self.par[x] = self.find(self.par[x])
            return self.par[x]

    # 併合
    def unite(self, x, y):
        x = self.find(x)
        y = self.find(y)
        if x == y:
            return
        if self.rank[x] < self.rank[y]:
            self.par[x] = y
        else:
            self.par[y] = x
            if self.rank[x] == self.rank[y]:
                self.rank[x] += 1

    # xとyが同じ集合に属するかを判定（同じ根に属するか）
    def same(self, x, y):
        return self.find(x) == self.find(y)


N, M = map(int, input().split())
uf = UnionFind(N)

#print(uf.par)   # [0, 1, 2, 3, 4, 5] 併合前で親なし
#print(uf.rank)   # [0, 0, 0, 0, 0, 0] 木の深さは全て0

for _ in range(M):
    a, b = map(int, input().split())
    uf.unite(a-1, b-1)

#print(uf.par)   # [0, 0, 0, 3, 4, 4]
#print(uf.rank)   # [1, 0, 0, 0, 1, 0]

ans = -1

for i in range(N):
  if uf.par[i] == i:
    ans += 1

print(ans)

まとめ

情報科学初心者でしたが、アルゴリズムを勉強するのは役に立つとか立たないとか抜きに、シンプルに面白いなと感じています。その上でよく言われることですが、初歩的なことは絶対分かってて損はないし、業務でもその感覚は役に立つと感じています。それと単純に競プロはコーティングの練習になると思います。
　レートの伸びは対数関数的で、これから成績上げてくのは大変そうですが、頑張って次のレベル（水色）目指したいと思います。