⚠️ 注意
本記事はアイデア段階の考察をまとめたもので、厳密性に欠ける部分や誤りを含む可能性があります。
誤りのご指摘やご意見をいただけると大変ありがたいです。
考えがまとまり次第修正を加えていきます。
はじめに
初めまして,Takamitsuです.今回はスライディングモード制御が最適制御問題からどのように導出されるかを示してみたいと思います.
スライディングモード制御は制御器の値を高速に切り替えることで,系をある切替平面(切替線,切替超平面)上に到達させ,その上で安定な運動を実現する手法です.一方で,最適制御問題では目的関数の形により最適な入力の性質が決まります.本投稿では「なぜ最適性を追うことでスライディングモード制御のような離散的な最適入力になるのか」を数学的に導出し,シミュレーション上で比較・検証します.
最適制御問題
最適制御問題の定式化
可制御な制御対象
\dot{x}(t) = Ax(t)+Bu(t), \quad t\geq0, \quad x(0)=x_0 \in\mathbb{R}^d
に対して,終端時間$T$が与えられたとき,
x(T) = 0
と達成する制御入力$u(t),\ t\in[0,T]$で最大入力$u_{\max}$に対し,
|u(t)|\leq u_{\max},\quad \forall t\in[0,T]
を満たし,かつ以下の目的関数
J(x,u) = \int_0^T L(x(t),u(t))dt
を最小化する解を最適制御という.また,このような目的関数を最小化する問題を最適制御問題という.
ポントリャーギンの最小原理
ハミルトニアンと呼ばれる以下の関数を定義する.
H(x,p,u):= L(x(t),u(t)) + p^\top (Ax+Bu)
ここで,$p$とは共状態と呼ばれる変数で,最適化問題におけるラグランジュ未定乗数に相当する.
最適制御問題の解が存在すると仮定し,それを$u^*(t)$とおくと,以下の連立微分方程式を満たす.
\dot{x}^*(t) = \frac{\partial H}{\partial p}(x^*(t),p^*(t),u^*(t))
\dot{p}^*(t) = -\frac{\partial H}{\partial x}(x^*(t),p^*(t),u^*(t))
ここで,$x^*(t)$は最適状態を表す.
また,最適制御入力は各時刻でハミルトニアンを最小化するため,以下のように書ける.
u^*(t) = \arg\min_{|u|\leq u_{\max}}H(x^*(t),p^*(t),u)
| 注意:本稿で取り上げたポントリャーギンの最小原理は,導出に必要な部分を抜粋したものであり,定理の詳細を知りたい場合は以下の書籍などを参考にしてください. |
|---|
最適制御問題からのスライディングモード制御の導出
スライディングモード制御の基本的な考え方
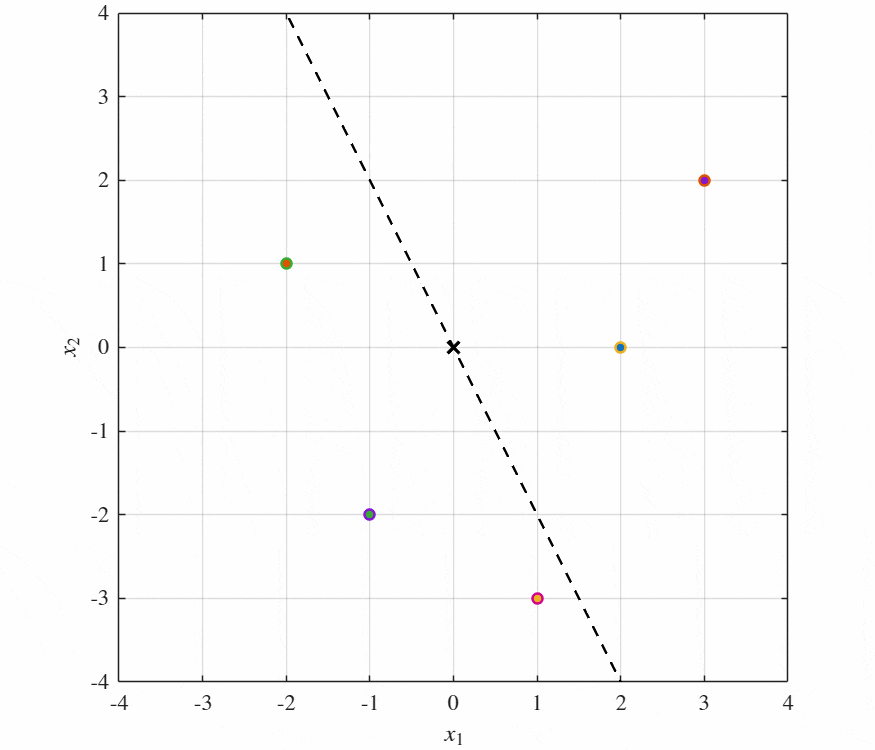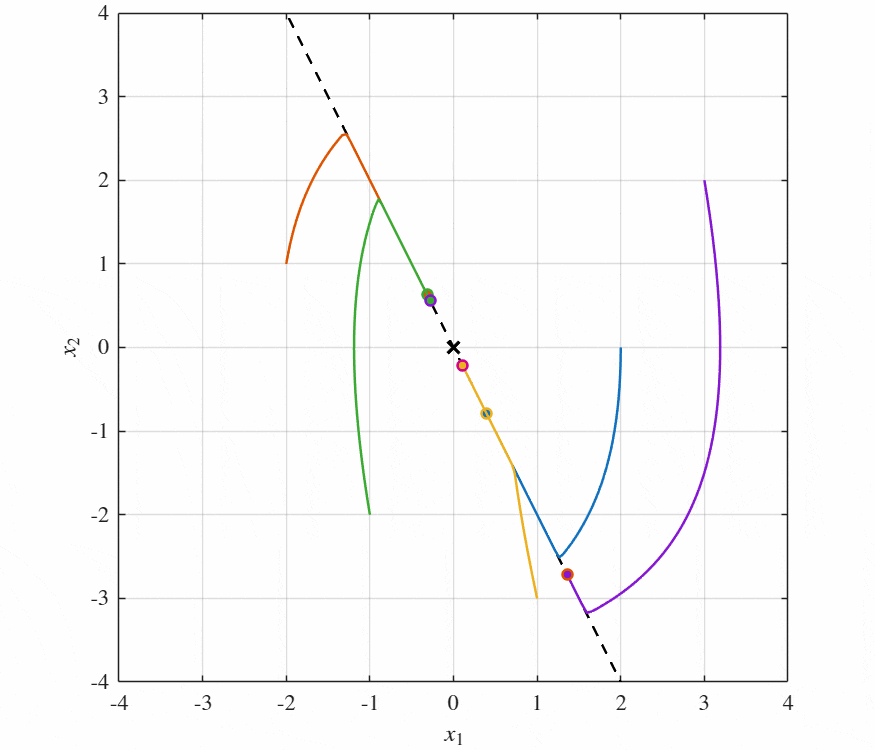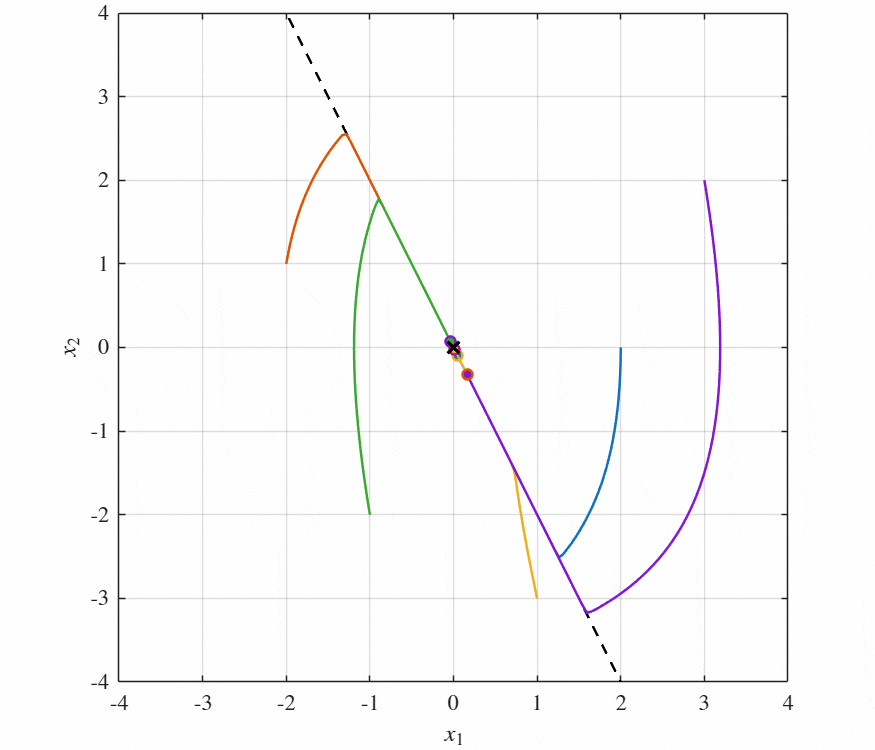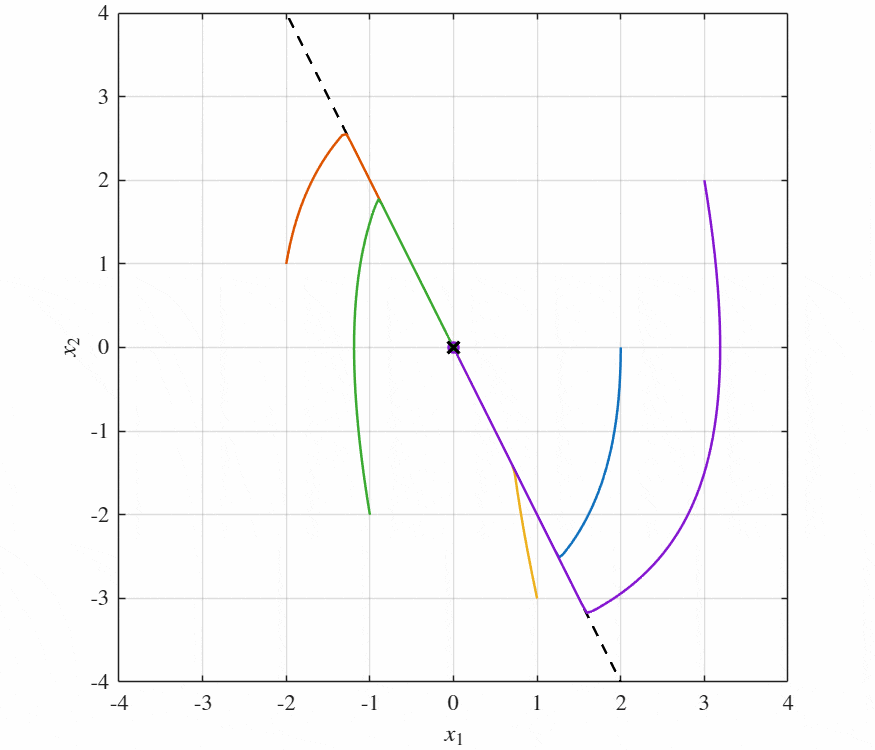
スライディングモード制御は,システムの状態を狙った切替線(切替平面)に素早く到達させる到達モードと到達後の状態が直線上を原点に向かっていく滑りモード(sliding mode)の二段階に分かれる.以下にシステムの位相空間上での挙動を示す.
このように任意の場所から出発した軌跡は切替線に向かって動き,切替線へ到達後,原点に向かって漸近的に近づく.ここで,切替関数と呼ばれる$\sigma(x)$を以下のように定義する.
\sigma(x)=Sx
ここで,$S$は行ベクトルである.特に,$\sigma(x)=0$となるときを切替平面といい,この切替平面を境界として制御入力$u$の正負を切り替える.
本稿では,この切替関数$\sigma(x)$を用いて最適制御問題の目的関数$J(x,u)$を設計することで,スライディングモード制御を導出する.
目的関数の設定
最適制御問題における目的関数を以下のように設定する.
\displaylines{
J(x) &= \int_0^T |\sigma(x)|dt \\
&=\int_0^T |Sx|dt
}
この目的関数の意味は「切替平面に素早く到達させ,切替平面上にある状態を維持しようとする」になる.
スライディングモード制御の制御入力の導出
ここで,ハミルトニアンは
H(x,p,u) := |Sx| + p^\top(Ax+Bu)
となり,ポントリャーギンの最小原理より,最適制御入力$u^*(t)$は,
\displaylines{
u^*(t) = \arg\min_{|u|\leq u_{\max}}H(x^*,p^*,u)\\
\qquad\qquad\qquad\qquad= \arg\min_{|u|\leq u_{\max}}\{|Sx^*| + p^{*\top}(Ax^*+Bu)\}\\
= \arg\min_{|u|\leq u_{\max}}p^{*\top} Bu \\
= -u_\max \text{sgn}(p^{*\top} B)
}
と表すことができる.次に,共状態$p^*$を求める.ポントリャーギンの最小原理より,共状態の微分方程式は,
\displaylines{
\dot{p}^*(t) = -\frac{\partial H}{\partial x}(x^*(t),p^*(t),u^*(t))\\
\qquad\quad=-\text{sgn}\{Sx^*(t)\}S^\top- A^\top p^*(t)
}
である.終端条件を$p^*(T)=0$と仮定すると,微分方程式の解析解は,
\displaylines{
\qquad \quad p^*(t)=e^{-A^\top t}p^*(T)-\int_T^t e^{-A^\top (t-\tau)}\text{sgn}(Sx^*)S^\top d\tau\\
=\int_t^T e^{-A^\top (t-\tau)}\text{sgn}(Sx^*)S^\top d\tau
}
である.したがって,最適制御入力$u^*$は
\displaylines{
u^*(t) = -u_\max \text{sgn}(p^{*\top} B)\\
\qquad\qquad\qquad\qquad\qquad\quad = -u_\max\text{sgn}\{\int_t^T \text{sgn}(Sx^*(\tau))Se^{-A^\top (t-\tau)}Bd\tau\}
}
である.ここで,$t<\tau\leq T$は未来の時刻であるため,未来の時刻においては実用上$Sx^*(\tau)=0$と仮定すると,現在の時刻$t$の場合のみ考えればよいので,
u(t)= -u_\max\text{sgn}\{\text{sgn}(Sx(t))SB\}
であるので,設計上$SB>0$を保証すると,
u(t)= -u_\max\text{sgn}(Sx(t))
というスライディングモード制御の制御入力が得られる.ここで注意するべきはこの制御入力がいくつかの仮定の下での近似であるため,最適な制御入力$u^*$ではないことである.ここで行った近似は実用的な直感を説明するためのものであり,厳密な最適性を主張するものではない.
シミュレーション
ここでは,厳密な解析解から得られた最適制御入力$u^*$といくつかの仮定の下での近似であるスライディングモード制御の制御入力$u$を用いたシミュレーションを比較する.
Optimal Input1を
u^*(t) = -u_\max\text{sgn}\{\int_t^T \text{sgn}(Sx^*(\tau))Se^{-A^\top (t-\tau)}Bd\tau\}
とし,Input2を
u(t)= -u_\max\text{sgn}(Sx(t))
とすると,シミュレーションは以下のようになる.
このように最適制御入力$u^*$とスライディングモード制御の制御入力$u$は制御性能にほぼ差がないとわかった.
さいごに
最適制御問題の定式化からスライディングモード制御の導出を行い,最適制御入力とスライディンモード制御の制御入力を用いてシミュレーションし,制御性能の差を比較・検証してみました.
本投稿の内容に関するご質問/ご指摘等もお待ちしております.
参考文献
[1] 永原 正章,"スパースモデリング",コロナ社,2017.
[2] 野波 健蔵,"スライディングモード制御入門",コロナ社,2024.
ソースコード
clear
close all
A = [0 1; -1 1];
B = [0; 1];
x0 = [1; 1];
S = [1 1];
ts = 0;
tf = 5;
h = 0.001;
t = ts:h:tf;
x1 = x0;
x1_str = zeros(2,length(t));
x1_str(:,1) = x1;
x2 = x0;
x2_str = zeros(2,length(t));
x2_str(:,1) = x2;
u_max = 10;
p = [0; 0];
for step = 2:length(t)
disp(step)
u1 = - u_max*sign(S*x1);
dx1 = A*x1 + B*u1;
x1 = x1 + dx1*h;
x1_str(:,step) = x1;
sigma = 0;
for tau = tf:-h:t(step)
dp = - sign(S*x2)*S.' - A.'*p;
p = p - dp*h;
sigma = sigma + sign(S*x2)*S*exp(-A*(t(step)-tau))*B;
end
u2 = - u_max*sign(sigma);
dx2 = A*x2 + B*u2;
x2 = x2 + dx2*h;
x2_str(:,step) = x2;
end
figure('Position',[50 50 1000 700])
tiledlayout(2,2)
nexttile(1)
plot(t,x2_str)
xlabel('Time $t$')
ylabel('State $x$')
title('Time Series Response with Optimal Input 1')
nexttile(2)
plot(x2_str(1,:),x2_str(2,:))
axis equal
xlabel('$x_1$')
ylabel('$x_2$')
title('Phase Plot with Optimal Input 1')
nexttile(3)
plot(t,x1_str)
xlabel('Time $t$')
ylabel('State $x$')
title('Time Series Response with Input 2 (SMC)')
nexttile(4)
plot(x1_str(1,:),x1_str(2,:))
axis equal
xlabel('$x_1$')
ylabel('$x_2$')
title('Phase Plot with Input 2 (SMC)')