LoginSignup
0
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@Tadataka_Takahashi

Pythonで隣接行列を使ったグラフの数値化：基本を試す

Posted at

はじめに

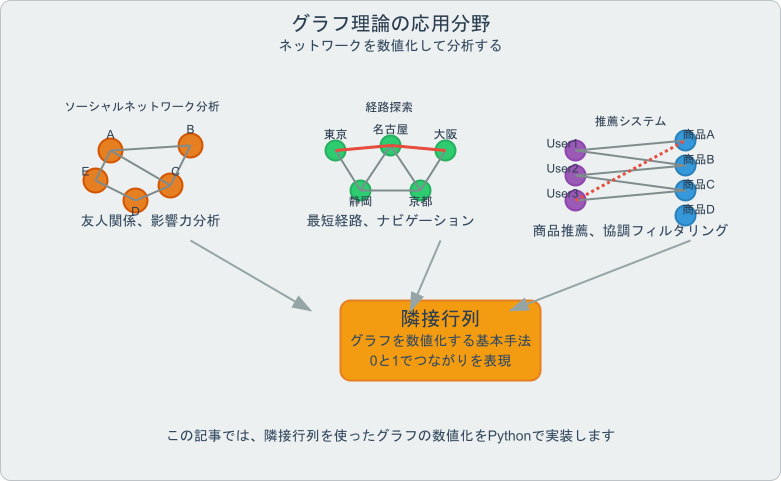
graph_intro_diagram.png

グラフ理論は、ソーシャルネットワーク分析、推薦システム、経路探索など、様々な分野で活用される重要な数学的概念です。しかし、グラフをコンピュータで扱うためには、まず数値化する必要があります。

この記事では、グラフを数値化する最も基本的な方法である隣接行列（Adjacency Matrix）について、手書きの図からPythonコードまで、段階的に解説していきます。

隣接行列とは何か

直感的な理解：手書きで考えてみよう

まず、簡単なグラフを手書きで描いてみましょう。

    A ---- B
    |      |
    |      |
    C ---- D

このグラフには4つのノード（A, B, C, D）があり、以下の接続関係があります：

  • A と B が繋がっている
  • A と C が繋がっている
  • B と D が繋がっている
  • C と D が繋がっている

隣接行列への変換

この接続関係を行列で表現すると、以下のようになります：

     A  B  C  D
A [  0  1  1  0 ]
B [  1  0  0  1 ]
C [  1  0  0  1 ]
D [  0  1  1  0 ]

読み方のルール：

  • 行列の要素 [i][j] が 1 → ノード i とノード j が繋がっている
  • 行列の要素 [i][j] が 0 → ノード i とノード j が繋がっていない
  • 対角線要素は通常 0（自分自身との接続は考えない）

NetworkXで隣接行列を扱う

基本的なコード例

NetworkXを使って、実際にグラフを作成し隣接行列を取得してみましょう。

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt

# グラフを作成
G = nx.Graph()

# ノードとエッジを追加
G.add_nodes_from(['A', 'B', 'C', 'D'])
G.add_edges_from([('A', 'B'), ('A', 'C'), ('B', 'D'), ('C', 'D')])

# グラフを可視化
plt.figure(figsize=(8, 6))
pos = nx.spring_layout(G, seed=42)
nx.draw(G, pos, with_labels=True, node_color='lightblue', 
        node_size=1000, font_size=16, font_weight='bold')
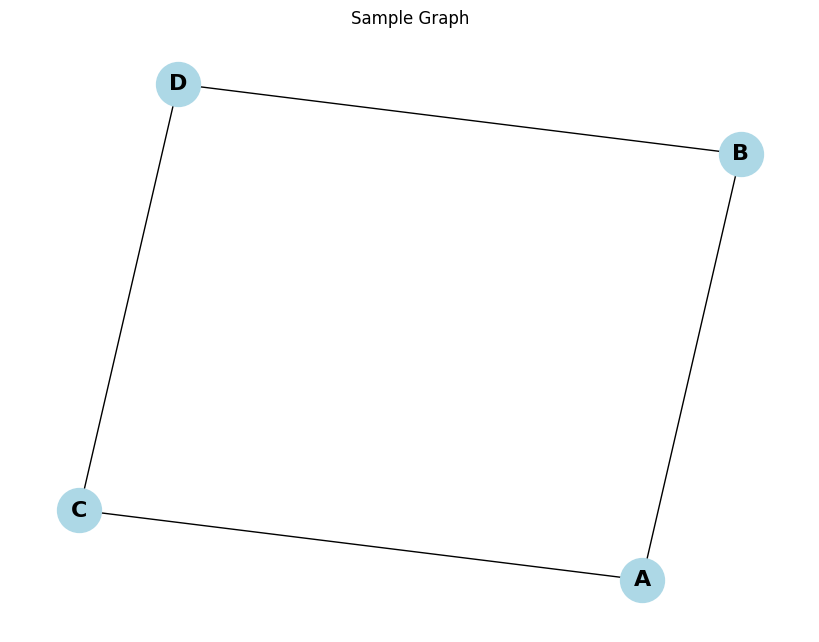
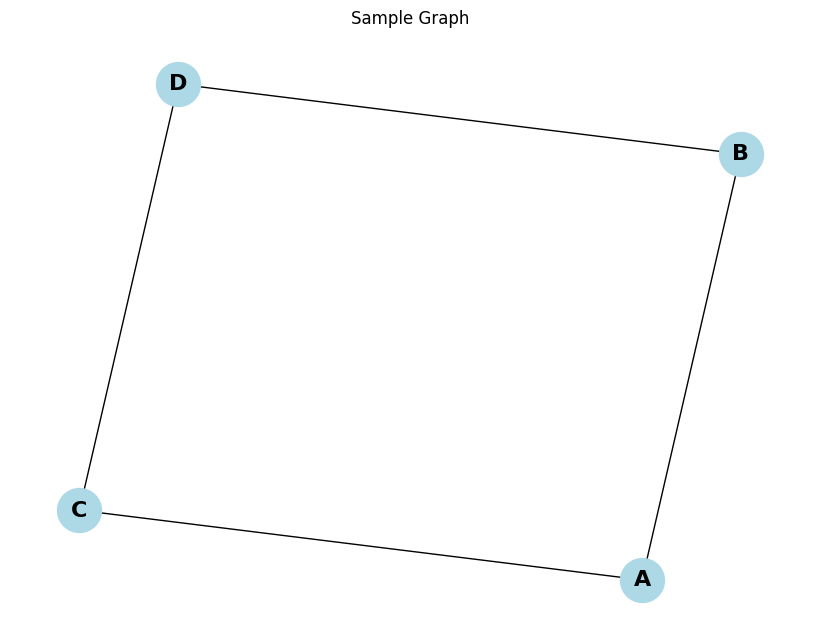
plt.title("Sample Graph")
plt.show()

# ノード順序を明示的に指定（重要！）
node_order = ['A', 'B', 'C', 'D']

# 隣接行列を取得（NetworkX 3.0+ 推奨方法）
try:
    # 最新版の推奨方法
    adjacency_matrix = nx.to_scipy_sparse_array(G, nodelist=node_order)
except AttributeError:
    # 古いバージョンとの互換性
    adjacency_matrix = nx.adjacency_matrix(G, nodelist=node_order)

print("隣接行列（スパース形式）:")
print(adjacency_matrix)

# 密行列として表示
dense_matrix = adjacency_matrix.todense()
print("\n隣接行列（密行列形式）:")
print(dense_matrix)

print(f"\nノード順序: {node_order}")

出力例：

image.png

隣接行列（スパース形式）:
  (0, 1)	1
  (0, 2)	1
  (1, 0)	1
  (1, 3)	1
  (2, 0)	1
  (2, 3)	1
  (3, 1)	1
  (3, 2)	1

隣接行列（密行列形式）:
[[0 1 1 0]
 [1 0 0 1]
 [1 0 0 1]
 [0 1 1 0]]

ノード順序: ['A', 'B', 'C', 'D']

⚠️ ノード順序の重要性

隣接行列ではノード順序が重要です。nodelist パラメータを指定しないと、ノードの順序が予期しないものになる可能性があります：

# ノード順序を指定しない場合（推奨しない）
adj_unordered = nx.to_scipy_sparse_array(G).todense()
actual_order = list(G.nodes())

print("ノード順序を指定しない場合:")
print(f"実際のノード順序: {actual_order}")
print("隣接行列:")
print(adj_unordered)

# ノード順序を指定する場合（推奨）
desired_order = ['A', 'B', 'C', 'D']
adj_ordered = nx.to_scipy_sparse_array(G, nodelist=desired_order).todense()

print("\nノード順序を指定した場合:")
print(f"指定した順序: {desired_order}")
print("隣接行列:")
print(adj_ordered)

image.png

有向グラフ vs 無向グラフの違い

無向グラフ（Undirected Graph）

これまでの例は無向グラフでした。無向グラフの隣接行列には以下の特徴があります：

  • 対称行列：matrix[i][j] = matrix[j][i]
  • A→B の接続があれば、必ず B→A の接続もある
# 無向グラフの例
G_undirected = nx.Graph()
G_undirected.add_edges_from([('A', 'B'), ('B', 'C')])

node_order = ['A', 'B', 'C']
adj_undirected = nx.to_scipy_sparse_array(G_undirected, nodelist=node_order).todense()

print("無向グラフの隣接行列:")
print(adj_undirected)
print("対称性の確認:", np.array_equal(adj_undirected, adj_undirected.T))

出力例：

無向グラフの隣接行列:
[[0 1 0]
 [1 0 1]
 [0 1 0]]
対称性の確認: True

有向グラフ（Directed Graph）

有向グラフでは、矢印の方向が重要になります。

# 有向グラフの例
G_directed = nx.DiGraph()  # DiGraphを使用
G_directed.add_edges_from([('A', 'B'), ('B', 'C'), ('C', 'A')])

node_order = ['A', 'B', 'C']
adj_directed = nx.to_scipy_sparse_array(G_directed, nodelist=node_order).todense()

print("有向グラフの隣接行列:")
print(adj_directed)
print("対称性の確認:", np.array_equal(adj_directed, adj_directed.T))

# 可視化
plt.figure(figsize=(8, 6))
pos = nx.spring_layout(G_directed, seed=42)
nx.draw(G_directed, pos, with_labels=True, node_color='lightcoral',
        node_size=1000, font_size=16, font_weight='bold', 
        arrows=True, arrowsize=20)
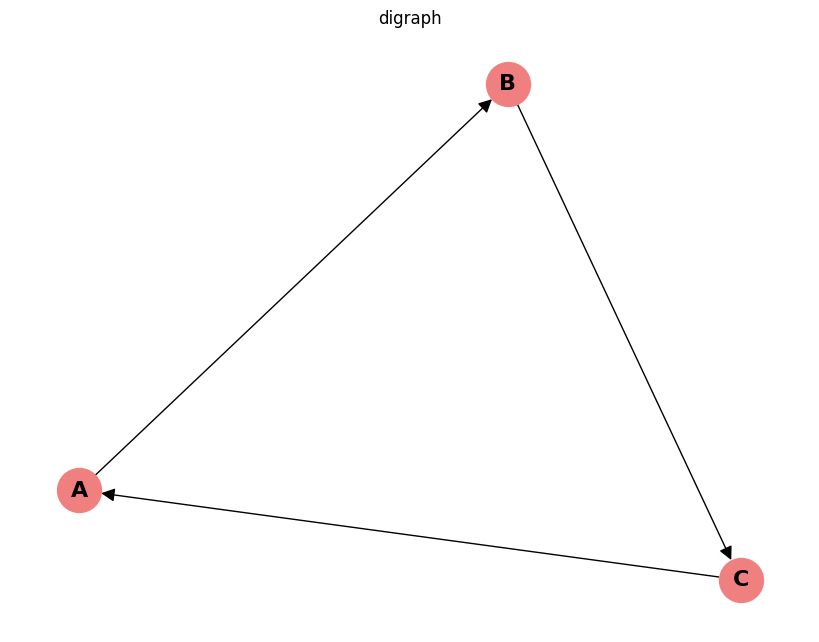
plt.title("digraph")
plt.show()

image.png

出力例：

有向グラフの隣接行列:
[[0 1 0]
 [0 0 1]
 [1 0 0]]
対称性の確認: False

注目点：この行列は対称ではありません！A→Bの接続はあるが、B→Aの接続はないためです。

スパース行列の活用

実際のネットワークでは、多くの場合、接続の数は全可能接続数に比べて非常に少なくなります。このような「疎な」グラフでは、スパース行列が効率的です。

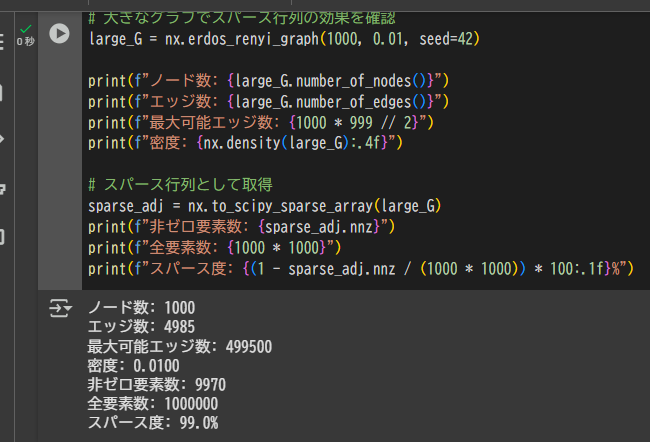
# 大きなグラフでスパース行列の効果を確認
large_G = nx.erdos_renyi_graph(1000, 0.01, seed=42)

print(f"ノード数: {large_G.number_of_nodes()}")
print(f"エッジ数: {large_G.number_of_edges()}")
print(f"最大可能エッジ数: {1000 * 999 // 2}")
print(f"密度: {nx.density(large_G):.4f}")

# スパース行列として取得
sparse_adj = nx.to_scipy_sparse_array(large_G)
print(f"非ゼロ要素数: {sparse_adj.nnz}")
print(f"全要素数: {1000 * 1000}")
print(f"スパース度: {(1 - sparse_adj.nnz / (1000 * 1000)) * 100:.1f}%")

出力例：

ノード数: 1000
エッジ数: 4996
最大可能エッジ数: 499500
密度: 0.0100
非ゼロ要素数: 9992
全要素数: 1000000
スパース度: 99.0%

このように、99%以上の要素が0なので、スパース行列が非常に有効です。

image.png

実践的な応用例

最短経路の探索

隣接行列を使って、2点間の最短経路を見つけることができます。

# 都市間の接続グラフ
city_graph = nx.Graph()
cities = ['NYC', 'LA', 'Chicago', 'Miami', 'Seattle']
connections = [('NYC', 'LA'), ('NYC', 'Chicago'), 
               ('LA', 'Chicago'), ('LA', 'Miami'),
               ('NYC', 'Seattle')]

city_graph.add_nodes_from(cities)
city_graph.add_edges_from(connections)

# 隣接行列（都市名順で固定）
adj_matrix = nx.to_scipy_sparse_array(city_graph, nodelist=cities).todense()
print("都市間接続の隣接行列:")
print(f"都市順序: {cities}")
print(adj_matrix)

# 最短経路
shortest_path = nx.shortest_path(city_graph, 'Seattle', 'Miami')
path_length = nx.shortest_path_length(city_graph, 'Seattle', 'Miami')

print(f"\nSeattleからMiamiへの最短経路: {' → '.join(shortest_path)}")
print(f"経路長: {path_length}")

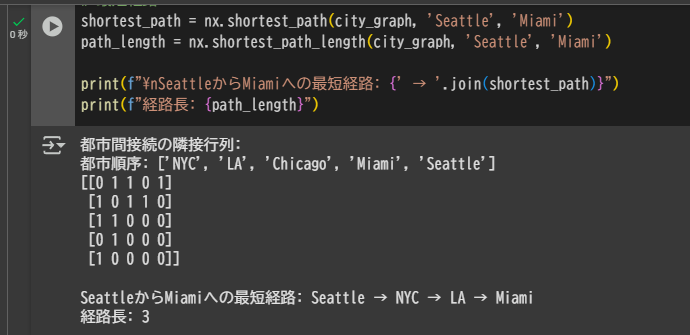
出力例：

image.png

都市間接続の隣接行列:
都市順序: ['NYC', 'LA', 'Chicago', 'Miami', 'Seattle']
[[0 1 1 0 1]
 [1 0 1 1 0]
 [1 1 0 0 0]
 [0 1 0 0 0]
 [1 0 0 0 0]]

SeattleからMiamiへの最短経路: Seattle → NYC → LA → Miami
経路長: 3

グラフの特性分析

# グラフの基本特性を隣接行列から分析
def analyze_graph(G, node_order=None):
    if node_order is None:
        node_order = list(G.nodes())
    
    adj = nx.to_scipy_sparse_array(G, nodelist=node_order)
    
    # 次数（各ノードの接続数）
    degrees = np.array(adj.sum(axis=1)).flatten()
    
    print(f"各ノードの次数:")
    for node, degree in zip(node_order, degrees):
        print(f"  {node}: {degree}")
    
    print(f"平均次数: {np.mean(degrees):.2f}")
    print(f"最大次数: {np.max(degrees)}")
    print(f"最小次数: {np.min(degrees)}")
    
    return degrees

print("都市グラフの分析:")
degrees = analyze_graph(city_graph, cities)

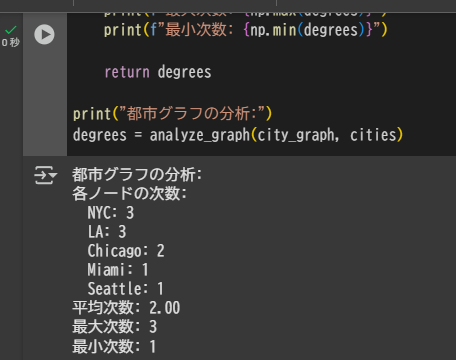
image.png

出力例：

都市グラフの分析:
各ノードの次数:
  NYC: 3
  LA: 3
  Chicago: 2
  Miami: 1
  Seattle: 1
平均次数: 2.00
最大次数: 3
最小次数: 1

自己ループを持つグラフ

特殊なケースとして、自己ループ（self-loop）を持つグラフを見てみましょう：

# 自己ループを持つグラフ
G_selfloop = nx.Graph()
G_selfloop.add_edges_from([('A', 'B'), ('B', 'C'), ('A', 'A')])  # A-A が自己ループ

# ノード順序を確認
node_order = sorted(G_selfloop.nodes())  # アルファベット順にソート
print(f"ノード順序: {node_order}")

adj_selfloop = nx.to_scipy_sparse_array(G_selfloop, nodelist=node_order).todense()
print("自己ループを持つ隣接行列:")
print(adj_selfloop)

# 自己ループの確認
a_index = node_order.index('A')
print(f"ノード A の自己ループ: {adj_selfloop[a_index, a_index]}")

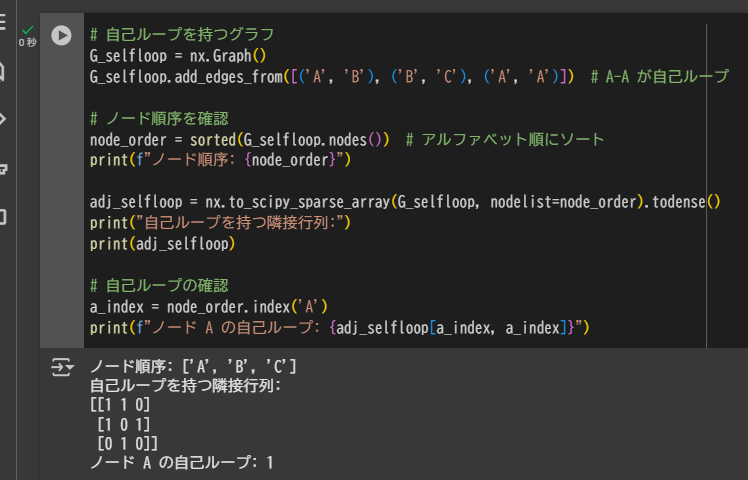
出力例：

image.png

ノード順序: ['A', 'B', 'C']
自己ループを持つ隣接行列:
[[1 1 0]
 [1 0 1]
 [0 1 0]]
ノード A の自己ループ: 1

この場合、対角線要素 [0][0] が 1 になり、ノード A が自分自身と接続していることを表します。

まとめ

FireShot Capture 009 - 隣接行列まとめ図解 - [].png

この記事では、グラフを数値化する基本的な方法である隣接行列について学びました。

隣接行列は、グラフの接続関係を 0 と 1 で表す基本的な表現方法です。
無向グラフでは対称行列、有向グラフでは非対称行列となります。
実務ではノードの順序を明示的に指定することが重要で、nodelist パラメータを活用すると安全です。
また、大規模で疎なグラフではスパース行列を利用することで効率的に扱えます。
なお、NetworkX 3.0 以降では nx.to_scipy_sparse_array() の使用が推奨されているため、バージョン互換性にも配慮しましょう。

参考資料

0
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?