LoginSignup
71
51

More than 3 years have passed since last update.

RustAdvent Calendar 2020Day 6
@Surpris(Surpris)

『ゼロから作る Deep Learning』を読んで Rust で実装した話

Last updated at Posted at 2020-12-05

本記事は Rust Advent Calendar 2020 の６日目の記事です。
前日の記事はcipepser様による『Rustの可変長引数関数とHListの話』です。
翌日の記事はtermoshtt様による『Rust の Foreign Function Interface (FFI)』です。

変更履歴

変更ID 年月日 内容
1 2020/12/05 初版作成
2 2020/12/06 namn1125様のコメントを受けて、比較結果を cargo run --release したものに修正
3 2020/12/06 レイヤーが受けるデータ型を Array2 に統一したときの訓練速度を比較結果に追記

本記事のまとめ

リポジトリについて

本編の目次

  1. 動機
  2. 実装の基本方針
  3. モデルの実装
    1. データ型
    2. レイヤーモデル
    3. 順伝播と誤差逆伝播
  4. ポイント
    1. 実装が必要な関数
    2. ArrayとArrayViewの変換
    3. Array2とArrayDの変換
    4. Arrayから無作為に要素を抽出する方法
  5. ベンチマーク
  6. おわりに
  7. 参考
    1. 先駆者の方々
    2. Rustで使える深層学習フレームワーク

動機

これまで Keras in TensorFlow を使用して深層学習で遊ぶ側でしたが、内部の動作（例えば誤差逆伝播）の実装方法についてはからっきしでした。
ちょうど Rust を勉強しているところであり、深層学習モデルの実装が Rust の学習において良い題材になると思い、実装にチャレンジしました。

実装の基本方針

今回の実装の基本方針は次の通りです。

  1. できるだけ Rust-native なコードにする。
    今回、他のプログラミング言語で作成されたライブラリに対する Rust bindings を作成しませんでした。また、Rust bindings の使用をできるだけ控えました。例えば NumPy の Rust binding である rust-numpy は使用していません。
  2. unsafe なコーディングは陽には行わない。
    筆者がまだ Rust に慣れていないので、unsafe なコーディングを行わないこととしました。使用する既存のクレート内で unsafe なコーディングがされているものは許容しました。

モデルの実装

データ型

今回、特徴量とラベルのデータ型として ndarray で実装されている型（Array 系）を採用しました。ndarray の利点として次が挙げられます。

  • 多次元配列が実装されている。
  • 代表的な配列演算が実装されている。

他の候補として配列と Vec が考えられましたが、以下に示す課題がありました。まず配列について、

  • コンパイル時にサイズが確定している必要がある。
  • 多次元配列の実装が面倒。
  • 基本的な配列間の演算を自前で実装する必要がある。
  • 関数が配列を戻り値にすることが難しい。
    • これは Box でラップする、参照を引数にとる、等の方法で解決できると思われます。

次に Vec について、

  • 多次元配列の実装が面倒。
  • 基本的な配列間の演算を自前で実装する必要がある。
    • もしかしたら既存のクレートで実装があるかもしれません。
  • 自前の実装では ndarray よりかなり処理速度が遅かった。
    • 実装次第では高速になると思います。

これらの課題を解決する手間と ndarray の利便性を鑑みて、ndarray を採用しました。

レイヤーモデル

参考書の４章および５章で採用されているモデルはレイヤーモデルです。今回の実装もこれに従います。
今回実装した三層パーセプトロンモデルは下図のようなレイヤー構成を持ちます。
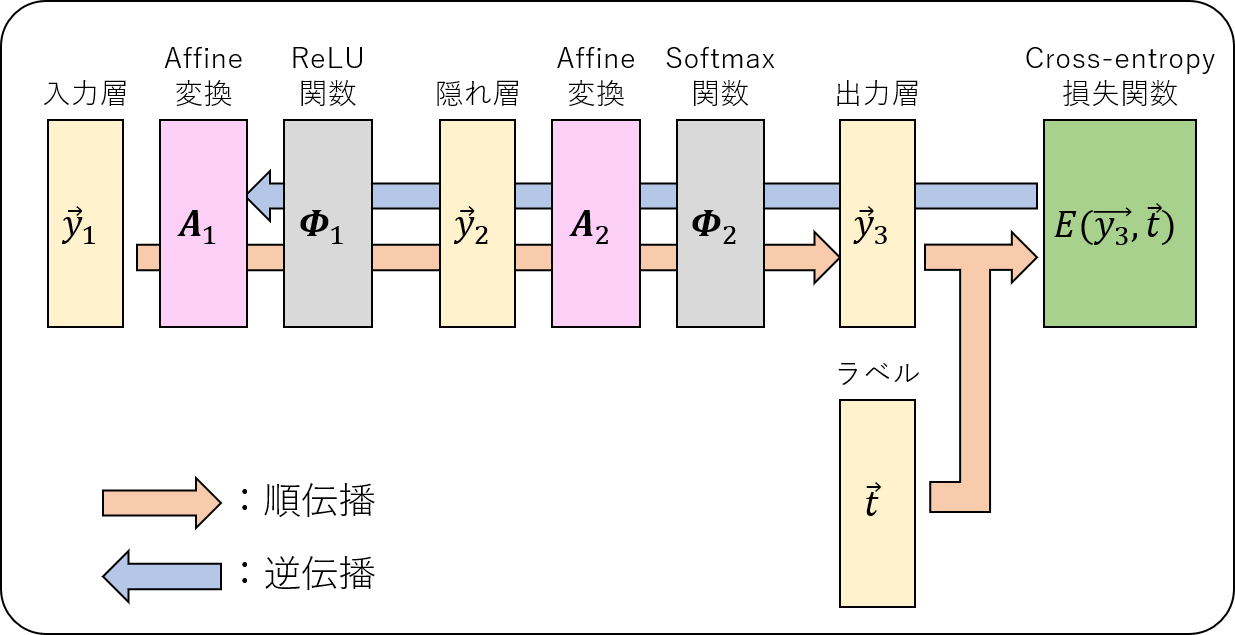
三層パーセプトロンモデル
※本記事において、$N$ 層のモデルとは、入力層、隠れ層、出力層の数の合計が $N$ であるモデルを指すものとします。

実装したレイヤー（構造体）を以下に挙げます。

  • Affine 変換 ${\mathbf A}(\vec{x}) = {\mathbf W}\vec{x} + \vec{b}$
    • ${\mathbf W}$：重み、$\vec{b}$：バイアス
  • 活性化関数 $\phi(x)$
    • ReLU：$\phi(x)=\left\{\begin{array}{cc} x & (x > 0) \\ 0 & (x \leq 0) \end{array}\right.$
    • Sigmoid：$\phi(x)=1/(1 + e^{-x})$
      • 今回のモデルでは使用していません。
    • Softmax：$\vec{x}=(x_1,x_2,\dots,x_n)\rightarrow \phi(x_k\lvert\vec{x}) = e^{x_k}/\sum_j e^{x_j}$
  • 損失関数
    • Cross-entropy loss：$E(\vec{y}, \vec{t}) = -\sum_k t_k\log y_k$
      • $\vec{y},\vec{t}$ はそれぞれ出力層の出力、ラベルを表します。
    • 簡単のため、softmax レイヤーと cross entropy error レイヤーを結合したレイヤーを採用しています。

各レイヤーに共通の関数はトレイトとして、次のような形式で実装しました。

pub trait LayerBase<T> {
    // 順伝播
    fn forward(&mut self, x: &ArrayD<T>) -> ArrayD<T>;
    // 逆伝播
    fn backward(&mut self, x: &ArrayD<T>, dx: &ArrayD<T>) -> ArrayD<T>;
    // レイヤーの重みの更新※
    fn update(&mut self, lr: T);
}

※今回実装した活性化関数レイヤーや損失関数レイヤーには必要ありませんが、便宜上共通関数として実装しました。

順伝播と誤差逆伝播

深層学習における出力の計算とモデルのパラメータの更新手順については、多くの方が記事にされています（Qiita 内であればこちらの記事やこちらの記事が参考になると思います）。ここでは軽く触れるに留めます。

順伝播

$k$ 層目の隠れ層のサイズを $L_k$ とします。次の二つの手順を繰り返すことで、入力 $\vec{y}_1$ に対して予測値 $\vec{y}_N$ を得ます。

  1. Affine 変換レイヤー ${\mathbf A}_k$ を通す：$\vec{v}_{k} = {\mathbf A}_k(\vec{y}_{k}) = {\mathbf W}_k\vec{y}_{k} + \vec{b}_k$
  2. 活性化関数レイヤー ${\mathbf \Phi}_k$ を通す：$\vec{y}_{k+1} = {\mathbf \Phi}_k(\vec{v}_k)$

誤差逆伝播

パーセプトロンモデルで更新されるのは Affine変換レイヤーの重み ${\mathbf W}_k = (w_{ij}^{(k)})$ とバイアス $\vec{b}_k = (b_1^{(k)},b_2^{(k)},\dots,b_{L_k}^{(k)})$ です。これらは次式のように損失関数の偏微分を用いて更新されます。
$$
w_{ij}^{(k)}\rightarrow w_{ij}^{(k)} - \epsilon\frac{\partial E}{\partial w_{ij}^{(k)}},\ b_j^{(k)} \rightarrow b_j^{(k)} - \epsilon\frac{\partial E}{\partial b_j^{(k)}}.
$$
ここで $\epsilon\ (> 0)$ は学習率です。
誤差逆伝播ですから、出力層に近い側から入力層に近い側へと誤差が伝播し、各層のパラメータが更新されます。
各層のパラメータの更新もまた層ごとに独立に実行できるため、update 関数を共通関数としてトレイトに実装しました。

さて、第 $N-1$ 層目に対応する Affine 変換レイヤーに対する誤差の偏微分を計算してみます。$E = E(\vec{y}_N, \vec{t})$ は一見 ${\mathbf W}_{N-1},\vec{b}_{N-1}$ に依らないように見えますが、
$$
\vec{y}_N = {\mathbf \Phi}_{N-1}(\vec{v}_{N-1}) = {\mathbf \Phi}_{N-1}({\mathbf W}_{N-1}\vec{y}_{N-1} + \vec{b}_{N-1})
$$
と表現できることを考慮すると、$E(\vec{y}_N, \vec{t})$ が ${\mathbf W}_{N-1},\vec{b}_{N-1}$ に依存することが分かります。よって偏微分の連鎖律より
$$
\begin{array}{rcl}
\frac{\partial E}{\partial w_{ij}^{(N-1)}} &=& \frac{\partial E}{\partial \vec{y}_N}\cdot\frac{\partial \vec{y}_{N}}{\partial \vec{v}_{N-1}}\cdot\frac{\partial \vec{v}_{N-1}}{\partial w_{ij}^{(N-1)}} = \sum_l \sum_m \frac{\partial E}{\partial y_l^{(N)}}\frac{\partial y_l^{(N)}}{\partial v_m^{(N-1)}}\frac{\partial v_m^{(N-1)}}{\partial w_{ij}^{(N-1)}},\\
\frac{\partial E}{\partial b_j^{(N-1)}} &=& \frac{\partial E}{\partial \vec{y}_N}\cdot\frac{\partial \vec{y}_{N}}{\partial \vec{v}_{N-1}}\cdot\frac{\partial \vec{v}_{N-1}}{\partial b_j^{(N-1)}} = \sum_l \sum_m \frac{\partial E}{\partial y_l^{(N)}}\frac{\partial y_l^{(N)}}{\partial v_m^{(N-1)}}\frac{\partial v_m^{(N-1)}}{\partial b_j^{(N-1)}}.
\end{array}
$$
上式のうち $\partial E/\partial \vec{y}_N$ は損失関数の偏微分、$\partial \vec{y}_{N}/\partial \vec{v}_{N-1}$ は活性化関数の偏微分、$\partial v_m^{(N-1)}/\partial w_{ij}^{(N-1)}$ および $\partial v_m^{(N-1)}/\partial b_j^{(N-1)}$ は Affine 変換の偏微分であり、それぞれ独立に計算できます。したがって、それぞれのレイヤーに偏微分操作を持たせるように誤差逆伝播の計算を実装することができます。このような背景があって、backward 関数を共通の関数としてトレイトに実装しました。

なお、残りのレイヤーのパラメータに対する誤差の偏微分も同様に計算できます。詳しくはこちらの記事をご参照ください。

ポイント

実装が必要な関数

便宜上、次の関数を MathFunc トレイトとして ndarray::{Array1, Array2, ArrayD} に実装しました。ArrayBase に実装するだけで良かったかもしれませんが、ちょっとうまく行きませんでした。この辺は将来的に修正したいところです。

  • 指数関数：$x \rightarrow \exp(x)$
  • 対数関数：$x \rightarrow \log_t(x)$
    • 自然対数を底とする対数関数：$x \rightarrow \log_e(x)$
pub trait MathFunc<T>{
    fn exp(&self) -> Self;
    fn log(&self, e: T) -> Self;
    fn log_natural(&self) -> Self;
}

今回、ラベルの形として one-hot 表現を採用しているため、予測結果を比較する際に argmax が必要になります。argmax は ndarray-stats の QuantileExt トレイトに実装されているので、それを利用しました。

ArrayとArrayViewの変換

今回、引数に ArrayD などの Array<A, D> = ArrayBase<OwnedRepr<A>, D> 系の型をとる関数を実装したのですが、ndarray の slice 系の関数が ArrayView<'a, A, D> = ArrayBase<ViewRepr<&'a A>, D> を返すので、その間の変換操作が必要になる場面が何度かありました。
ArrayView 系から Array 系に変換する関数が ndarray クレート内には無いようで、代替手段を見つけるのに苦労しました。
例えば次のように参照に定数を乗することで ArrayView を Array に変換できます。

let a: Array1<f32> = arr!(&[1.0, 2.0, 3.0]);
let b: Array1<f32> = 1.0 * &a.slice(s![..2]);

Array2とArrayDの変換

今回、三層パーセプトロンモデルで２次元 Affine 変換を採用しました。ndarray::Array2 には内積関数 dot が実装されていますが、ArrayD には実装されていません（もしかしたらテンソル積があるかもしれませんが、ちょっと見つけられていません）。
活性化関数などはできるだけ多次元配列に対応させたいということもあり、Array2 と ArrayD を互いに変換する必要が生じました。
ndarray クレート内に実装されている次の関数が前述の変換操作を実現します。

pub fn into_dimensionality<D2>(self) -> Result<ArrayBase<S, D2>, ShapeError>
where
    D2: Dimension,

Arrayから無作為に要素を抽出する方法

深層学習ではデータセットから無作為に抽出したサブセット（バッチ）を用いて訓練することがよくあります。Array に対して無作為抽出する方法を二つ紹介します。

方法１

一つ目は rand クレートを用いてインデックス配列を生成し、Array::select を用いる方法です。今回はこちらを使用しました。

// ArrayBase::select
pub fn select(&self, axis: Axis, indices: &[Ix]) -> Array<A, D>
where
    A: Copy,
    S: Data,
    D: RemoveAxis,

例えば次のように用います。

use rand::prelude::*;

const BATCH_SIZE: usize = 100;
const NBR_TRAIN_IMAGES: usize = 60000;
fn main() {
    let data_set: Array2<f32> = ...;
    let mut rng = thread_rng();
    let mut indices: Vec<usize> = vec![0usize; BATCH_SIZE];
    for jj in 0..BATCH_SIZE {
        indices[jj] = rng.gen_range(0, NBR_TRAIN_IMAGES);
    }
    let batch: Array2<f32> = data_set.select(Axis(0), &indices);
}

方法２

二つ目は ndarray-rand の sample_axis を使う方法です。こちらは ndarray リポジトリ内で管理されているクレートです。

pub fn sample_axis(
    &self,
    axis: Axis,
    n_samples: usize,
    strategy: SamplingStrategy
) -> Array<A, D>
where
    A: Copy,
    D: RemoveAxis,

こちらの使用例は Docs.rs や ndarray-rand リポジトリの tests/tests.rs に掲載されています。

ベンチマーク

Rust で三層パーセプトロンモデルを実装しましたが、元のコードでの実装と遜色ない性能を有してほしいところです。そこで以下のモデルを、訓練時間と確度（accuracy）の観点で比較しました。

  • Rust でデータ構造に ndarray を採用して実装したもの
    • 本リポジトリの ch05 に入っています。
    • src/main.rs で rs_deep::dlfs01::ch05::train_neural_net::main(); 以外をコメントアウトした状態で、リポジトリのベースディレクトリ内で cargo run --release を実行すれば動きます。
  • 元の Python コードでの実装
    • ベンチマーク用スクリプトはこちらです。
  • Keras in TensorFlow を用いて実装したもの
    • ベンチマーク用スクリプトはこちらです。

ベンチマークに用いた環境

対象 値
CPU Intel(R) Core(TM) i7-10510U @ 1.80 GHz
RAM 8.00 GB
OS Ubuntu 20.04 on WSL2
元のコード用 Python Python 3.7.9, NumPy 1.19.2
Keras in TensorFlow での実装用 Python Python 3.7.9, NumPy 1.19.2, TensorFlow 2.3.0
Rust 用 rustup 1.23.0, rustc 1.48.0

パラメータ

パラメータ 値
データセット MNIST
入力層のサイズ $L_1$ 784 (=28 × 28)
隠れ層のサイズ $L_2$ 50
出力層のサイズ $L_3$ 10
学習率 $\epsilon$ 0.1
訓練データセットの数 60,000
テストデータセットの数 10,000
バッチサイズ 100
イテレーション数 10,000
乱数の設定 なし

結果

測定結果の一例を下表に示します。ここで
　訓練時間＝「バッチサイズ分のデータの選択＋順伝播＋逆伝播＋パラメータ更新」×「イテレーション数」
です。

対象 CPU 使用率 訓練時間 (sec) 確度
元の Python コード ∼80% ∼10 train=0.9809, test=0.9708
Rust での実装（Array2 と ArrayD の混合） ∼20% 15.06 (debug だと 511) train=0.9437, test=0.934
Rust での実装（すべて Array2） ∼20% ∼10 train=0.9479, test=0.9422
Keras in TensorFlow ∼70% ∼10 train=0.9813, test=0.9709

Array2 と ArrayD の混合版では、訓練時間は約 1.5 倍かかりました。確度は0.035 程度劣ります。まだ実装に改善点がありそうです。
（2020/12/06 追記）レイヤーが受けるデータ型をすべて Array2 に統一すると、訓練時間が Python での実装と同等になりました。
また、CPU 使用率が Python のコードに比べて 1/4 位しかありません。CPU を有効に使用するという課題も見えてきました。

元の Python 実装が Keras での実装と同程度の訓練時間と精度が出ているのも興味深いです。
※Keras での実装は他の実装と完全に同一の操作が行われているわけではないので、その辺で多少の差がついているかもしれません。

おわりに

今回は三層パーセプトロンモデルを Rust で実装し、その性能を元のコードや Keras in TensorFlow での実装と比較しました。
元のコードに比べて遅いなど、今回の実装には改善点が多数ありますので修正を進める予定です。
例えば Array2 と ArrayD の間の変換（into_dimensionality）がバッチごとに入るので、Array2 に統一することで速くなるかもしれません（フレキシビリティは下がりますが）。
（2020/12/06 追記）実際、into_dimensionality に時間がかかるようです。
本記事の執筆時点では５章（三層パーセプトロンモデルの実装）までしか進められておりませんが、参考書の残りの章も進めて基本的なレイヤーの実装方法も身に着ける予定です。

また、参考書には以下の続編があります。これらも読んで Rust で実装してみようと考えています。

参考

先駆者の方々

本記事と同等のことは誰もが考えるだろうと思っていましたが、やはり先駆者がいらっしゃいました。そのうち Qiita 内に投稿されている記事を紹介いたします。

Rustで使える深層学習フレームワーク

Rust で使える深層学習のフレームワークには、例えば以下のものがあります。

  • Leaf
    • 現在は開発が止まっています。
  • juice
    • 上記 Leaf の後継のようです。
  • primitiv-rust
  • Rust language bindings for TensorFlow
    • 公式の Rust binding です。
    • コアな部分は開発が進んでいるようですが、examples が充実していません。
    • また、examples を動かすためのモデルは Python でコンパイルされるようです。
71
51
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
71
51