はじめに
弊社でも、機械学習を取りいれてビジネスを最適化する流れになってきているので(心配な部分あり、おもしろそうな部分ありです。。。)、
積読状態になっていたゼロから作るディープラーニングを本格的に学習していこうと思います。
そこで、この本ではPythonで実装しながら進んでいくのですが、最近学習しているRustを使用して、実装していこうと思います。
Deeplearningとは?
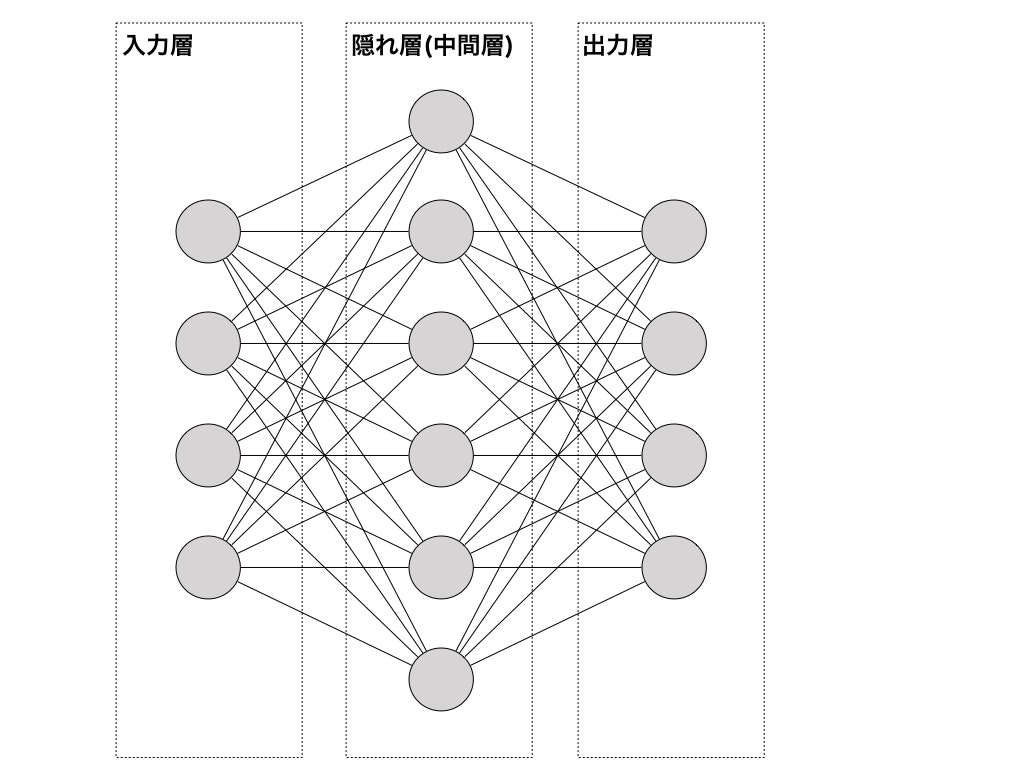
多層のニューラルネットワーク(脳のニューロンを模したもの)による機械学習手法。自動的に特徴量を抽出することができる等の特徴がある。
詳しくは、ディープラーニング参照。
環境
- macOS Sierra 10.12.6
- rustc 1.19.0
- crate gnuplot 0.0.22
- crate nalgebra 0.12.3
最初はディープラーニングで使用する行列演算に、rust-ndarrayを使用する予定だったのですが、様々な次元を扱うつもりで「ArrayD型」を使用し、実装を試みました。
その際、2✕2以上の積が計算できなかったので、nalgebraを使用しています。
(2✕2以上を計算しようとすると、not found function的なエラーが発生し、ビルドが通らなかったです。使い方が間違えていそう。)
ニューロンを実装してみる
まずは、ニューロンを実装してみます。
extern crate nalgebra;
use nalgebra::core::{DMatrix};
// ニューロン構造体.
pub struct Neuron<'a> {
bias: &'a DMatrix<f64>,
data: &'a DMatrix<f64>,
weight: &'a DMatrix<f64>,
}
// ニューロン実装.
impl<'a> Neuron<'a> {
pub fn new(bias: &'a DMatrix<f64>, data: &'a DMatrix<f64>, weight: &'a DMatrix<f64>) -> Self {
Neuron { bias: bias, data: data, weight: weight }
}
fn dot(&self) -> DMatrix<f64> {
self.data * self.weight + self.bias
}
// ステップ関数.
pub fn step(&self) -> DMatrix<f64> {
self.dot().map(|i| {
match i > 0. {
true => 1.,
false => 0.
}
})
}
// シグモイド関数.
pub fn sigmoid(&self) -> DMatrix<f64> {
self.dot().map(|i| { 1. / (1. + (-i).exp()) })
}
// ReLU関数.
pub fn relu(&self) -> DMatrix<f64> {
self.dot().map(|i| i.max(0.))
}
// 恒等関数.
pub fn identify(&self) -> DMatrix<f64> {
self.dot()
}
// ソフトマックス関数.
pub fn softmax(&self) -> DMatrix<f64> {
let _dot = self.dot();
let _max = _dot.iter().fold(0.0 / 0.0, |acc, i| i.max(acc) ); // NaNでないものを返す.
let _sum = _dot.iter().fold(0., |acc, i| (i - _max).exp() + acc);
_dot.map(|i| { (i - _max).exp() / _sum })
}
}
struct Neuronにバイアス、重み、インプットデータを持たせ、各種活性化関数を実装しました。
活性化関数とは?
入力信号の総和を出力信号に変換する関数です。入力信号の総和がどのように活性化するか(どのように発火するか)ということを決定する役割があります。
ステップ関数やシグモイド関数などの非線形関数があります。
なぜ、$y=cx$のような線形関数を使用しないのかというと、ニューラルネットワークで層を深くする意味がなくなる為です。
仮に、$y=cx$という活性化関数を使用すると、三層のニューラルネットワークを考えた場合、$y = c^{3}x$の計算を行うことになり、
これは、「$y=ax$」という形で表現できてしまい、三回演算する意味がなくなります。
これが、線形関数を使用しない理由となります。
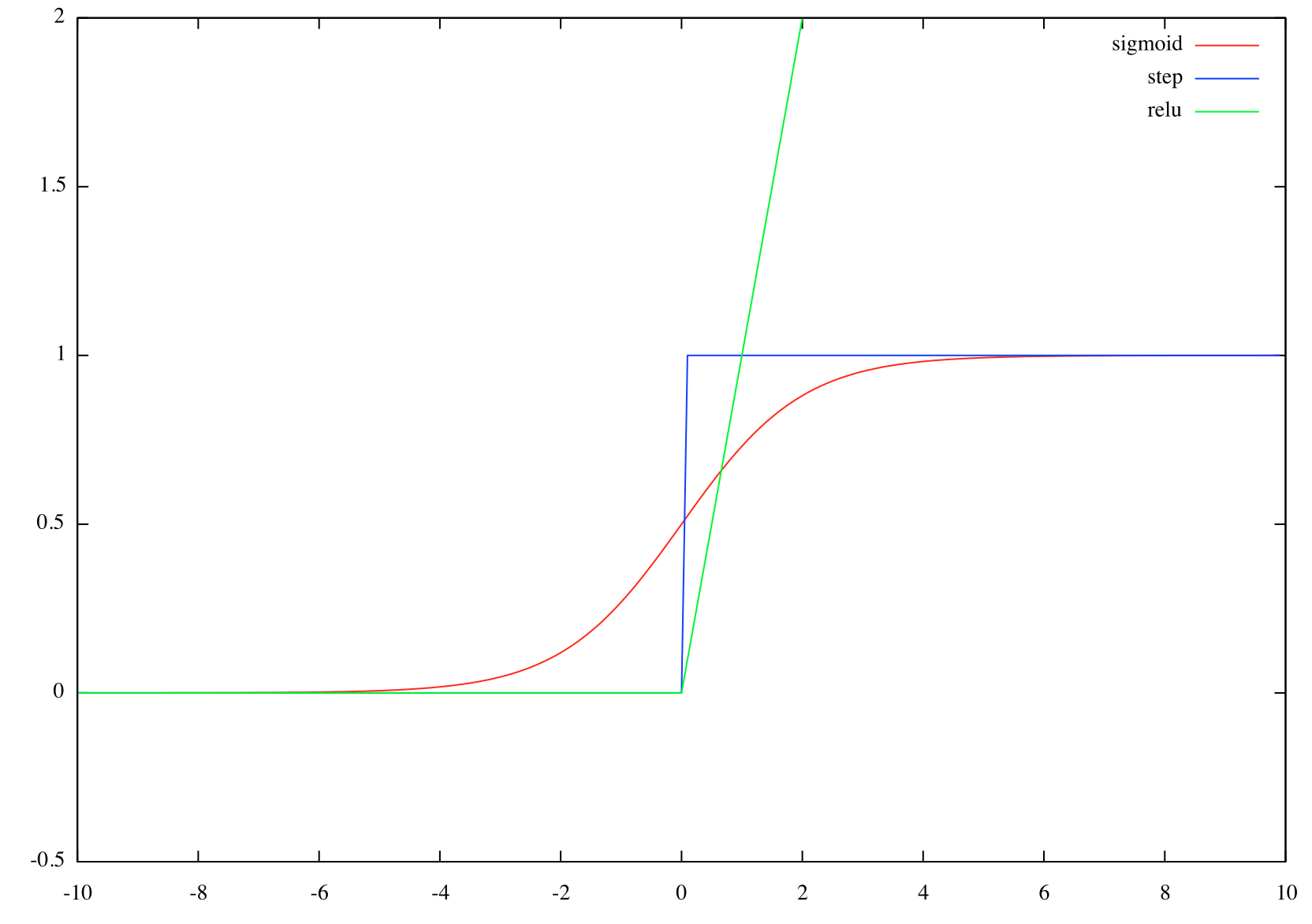
各活性化関数のグラフ
シグモイド関数、ステップ関数、ReLU関数をgnuplotでプロットしたものを記載します。
ステップ関数
h(x) = \left\{
\begin{array}{ll}
1 & (x \gt 0) \\
0 & (x \leq 0)
\end{array}
\right.
シグモイド関数
$$h(x) = \frac{1}{1+e^{-x}}$$
ReLU関数
h(x) = \left\{
\begin{array}{ll}
x & (x \gt 0) \\
0 & (x \leq 0)
\end{array}
\right.
単層、多層ニューラルネットワークを実装してみる
実装したNeuronを使用して、3.3.3/3.4.3を参照し、単層/多層ニューラルネットワークを実装してみます。
// 1層ニューラルネットワーク_
fn single_neural_nw() {
// 第一層入力データ.
let b1 = DMatrix::<f64>::from_iterator(1, 3, [0., 0., 0.].iter().cloned());
let x1 = DMatrix::<f64>::from_iterator(1, 2, [1., 2.].iter().cloned());
let w1 = DMatrix::<f64>::from_iterator(2, 3, [1., 2., 3., 4., 5., 6.].iter().cloned());
let n1 = neuron::Neuron::new(&b1, &x1, &w1);
// 出力層.
println!("identify:\n{}", n1.identify());
}
// 多層ニューラルネットワーク.
fn multi_neural_nw() {
let b1 = DMatrix::<f64>::from_iterator(1, 3, [0.1, 0.2, 0.3].iter().cloned());
let x1 = DMatrix::<f64>::from_iterator(1, 2, [1., 0.5].iter().cloned());
let w1 = DMatrix::<f64>::from_iterator(2, 3, [0.1, 0.2, 0.3, 0.4, 0.5, 0.6].iter().cloned());
let n1 = neuron::Neuron::new(&b1, &x1, &w1);
let b2 = DMatrix::<f64>::from_iterator(1, 2, [0.1, 0.2].iter().cloned());
let w2 = DMatrix::<f64>::from_iterator(3, 2, [0.1, 0.2, 0.3, 0.4, 0.5, 0.6].iter().cloned());
let x2 = n1.sigmoid();
let n2 = neuron::Neuron::new(&b2, &x2, &w2);
let b3 = DMatrix::<f64>::from_iterator(1, 2, [0.1, 0.2].iter().cloned());
let w3 = DMatrix::<f64>::from_iterator(2, 2, [0.1, 0.2, 0.3, 0.4].iter().cloned());
let x3 = n2.sigmoid();
let n3 = neuron::Neuron::new(&b3, &x3, &w3);
println!("identify:\n{}", n3.identify());
}
// main関数.
fn main() {
// 一層ニューラルネットワーク.
single_neural_nw();
// 多層ニューラルネットワーク.
multi_neural_nw();
}
以下、出力結果です。
identify:
┌ ┐
│ 5.000 11.000 17.000 │
└ ┘
identify:
┌ ┐
│ 0.317 0.696 │
└ ┘
書籍中の出力とほぼ同じ出力となったので、実装に間違いはなさそうです。
まとめ
今回は、第三章までをrustで実装してみました。
実際にニューラルネットワークを作成するよりも、nalgebraの使用方法が難しかったです(rustを熟知できていないから)。
次回はこの実装を元にして、勾配法を実装し、学習できるネットワークを作成していきたいと思います。