はじめに
本記事は、E資格取得講座のラビットチャレンジのレポートです。今回は深層学習 day1 の講義を受けてのレポートを提出します。
Section1:入力層~中間層
要点のまとめ
入力層とは、ニューラルネットワークに何かしらの数値の集まりを入力する層のこと。なお、入力層におけるノードとは、入力を受け取る箇所を指す。また、バイアスは通常入力とはみなさない。入力を$\boldsymbol{x}$、入力層における重みを$\boldsymbol{W}$、バイアスを$b$としたときに、$\boldsymbol{W}\boldsymbol{x}+b$を入力層から中間層に渡す。中間層においては、入力層から受け取った値を活性化関数で変換し、次のノードに順々に渡していく働きをする。
確認テスト
- この図式に動物分類の実例を入れてみよう。

- この数式をPythonで書け。
u = np.dot(W, x)+b
- 1-1のファイルから中間層の出力を定義しているソースを抜き出せ。
z = functions.relu(u)
ハンズオン
ハンズオン結果は下記。
ハンズオン
Section2:活性化関数
要点のまとめ
活性化関数とは、ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数。入力値の値によって、次の層への信号のON/OFFや強弱を定める働きをもつ。活性化関数には中間層用の関数と、出力層用の関数が存在する。
| 関数名 | 用途 | 値域 |
|---|---|---|
| ReLU関数 | 中間層 | $[0, +\infty]$ |
| シグモイド関数 | 中間層・出力層 | $[0, 1]$ |
| ステップ関数 | 中間層 | $[0, 1]$ |
| ソフトマックス関数 | 出力層 | $[0, 1]$ |
| 恒等写像 | 出力層 | $[-\infty, +\infty]$ |
なお、各関数の定義は下記となる。
- ReLU関数
\begin{eqnarray}
f(x)=
\begin{cases}
x & ( x>0 ) \\
0 & ( x\leq 0 )
\end{cases}
\end{eqnarray}
- シグモイド関数
f(x)= \frac{1}{1+e^{-x}}
- ステップ関数
\begin{eqnarray}
f(x)=
\begin{cases}
1 & ( x>0 ) \\
0 & ( x\leq 0 )
\end{cases}
\end{eqnarray}
- ソフトマックス関数
f(x_i) = \dfrac{e^{x_i}}{\sum_{k=1}^n e^{x_k}}
- 恒等写像
f(x) = x
確認テスト
- 線形と非線形の違いを図に書いて簡易に説明せよ。

- 配布されたソースコードより該当する箇所を抜き出せ。
z1 = functions.sigmoid(u)
ハンズオン
ハンズオン結果は下記。
ハンズオン
Section3:出力層
要点のまとめ
出力層とは、入力層によって入力された数値がニューラルネットワーク内を通過し、最終的に数値を出力する層を指す。例えば、動物の種類を分類するようなニューラルネットワークであれば、「入力された動物が〇〇である確率」といった形で出力される。
ニューラルネットワークは、誤差関数によってそのネットワークの精度を測定することができる。(後の講義で学ぶことだが、誤算関数を用いて、ニューラルネットワーク中のパラメータを調整する)誤算関数の定義は下記である。
$$E_n(\boldsymbol{w}) = \frac{1}{2}||\boldsymbol{y}-\boldsymbol{d}||^2$$
ただし、$\boldsymbol{y}$は入力に対する真値、$\boldsymbol{d}$は入力に対するニューラルネットワークの出力値である。
次に、出力層で用いられる活性化関数について述べる。
出力層で用いられる活性化関数は、信号の大きさがそのまま値の強弱となる。また、分類問題で確率の形での出力が必要な場合、出力を0~1の範囲に限定し、総和を1とする必要がある。
このように出力層では出力層ならではの制約が活性化関数に求められる。活性化関数の詳細については、本レポートのSection2:活性化関数で説明したので割愛する。
確認テスト
-
なぜ、引き算ではなく二乗するか述べよ。
引き算では、$\boldsymbol{y}-\boldsymbol{d}$の各成分の値が正負ばらばらのとき、各成分の和が相殺しあうことで真値と出力が異なる場合でも、誤算関数が0になる可能性があるから。 -
下式の1/2はどういう意味を持つか述べよ。
1/2があることで、微分の計算が容易になるから。(今後、ニューラルネットワーク中のパラメータを調整する際に、誤差関数の微分が必要になる。) -
(ソフトマックス関数について)①~③の数式に該当するソースコードを示し、一行ずつ処理の説明をせよ。
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x)/np.sum(np.exp(x), axis=0) #②はnp.exp(x)に部分。③はnp.sum(np.exp(x), axis=0)の部分。
return(y.T) #①はここ。ソフトマックス関数の返り値
x = x - np.max(x)
return(np.exp(x)/np.sum(np.exp(x))) #ここも①。ソフトマックス関数の返り値
- (交差エントロピーについて)①~②の数式に該当するソースコードを示し、一行ずつ処理の説明をせよ。
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size #①、②ともにここ
ハンズオン
ハンズオン結果は下記。(Section1のハンズオンに含まれているのでSection1と同じ)
ハンズオン
Section4:勾配降下法
要点のまとめ
ニューラルネットワークにおいては、誤差を最小にするようにパラメータを調整することが必要である。そこで用いられる手法が勾配降下法である。勾配降下法とは、パラメータを$k$回目のエポックから$k+1$回目のエポックに更新する際に、
$$\boldsymbol{\omega}^{(k+1)} = \boldsymbol{\omega}^{(k)} - \varepsilon \nabla E(\boldsymbol{\omega}^{(k)})$$
によって更新する手法をいう。$\varepsilon$は学習率、$\nabla E$は誤算関数の勾配で、
$$\nabla E(\boldsymbol{\omega}^{(k)}) = \dfrac{\partial E}{\partial \boldsymbol{\omega}} = \left[\dfrac{\partial E}{\partial \omega_1}, \cdots, \dfrac{\partial E}{\partial \omega_M}\right]_{|\boldsymbol{\omega}=\boldsymbol{\omega}^{(k)}}$$
である。勾配降下法は学習率$\varepsilon$の大きさによって収束の速度が大きく変わってしまう。例えば、学習率が大きすぎた場合、パラメータを更新するたびに、最適解を飛び越えてしまい、いつまでたっても収束しないなどの問題が発生する。逆に、学習率が小さすぎた場合、パラメータの更新がなかなか進まず、この場合もいつまでたっても収束しないなどの問題が発生する。
これらの問題を解決するために、勾配降下法を改良したアルゴリズムが複数提案されている。代表的なアルゴリズムは、
- 確率的勾配降下法(本レポートで説明)
- Momentum
- AdaGrad
- Adadelta
- Adam
である。Momentumより後のアルゴリズムについてはday2で学習する。
確率的降下法とは、勾配降下法では全てのデータに対して誤差関数の勾配を求めていたものを、ランダムに抽出したサンプルの勾配のみを用いてパラメータを更新する手法である。これによって、データが大きい場合でもパラメータを1回更新する際にかかる計算コストを減らすことができる。また、確率的降下法に比べ、選択するサンプルを増やした手法としてミニバッチ勾配降下法がある。ミニバッチ勾配降下法は、ランダムに分割したデータの集合に対してのみ勾配を計算し、パラメータを更新する手法である。これにより、並列計算を可能にする。
確認テスト
- 該当するソースコードを探してみよう。
network[key] -= learning_rate*grad[key]
-
オンライン学習とは何か。
新規に学習データが入手されるたび、モデルのパラメータを更新すること。 -
この数式の意味を図に書いて説明せよ。(この数式とは、$\boldsymbol{\omega}^{(t+1)} = \boldsymbol{\omega}^{(t)} -\varepsilon \nabla E_t$のこと)

ハンズオン
ハンズオン結果は下記。
ハンズオン
Section5:誤差逆伝播法
要点のまとめ
誤差逆伝播法とは、算出された誤差を、出力層側から順に微分し、前の層へと伝播していく手法。微分の値を再帰的に計算することができるので、最小限の計算で各パラメータでの微分値を計算できる。誤差逆伝播を実装する際には、下図のようなグラフを作成し、それを基に実装することが多い。
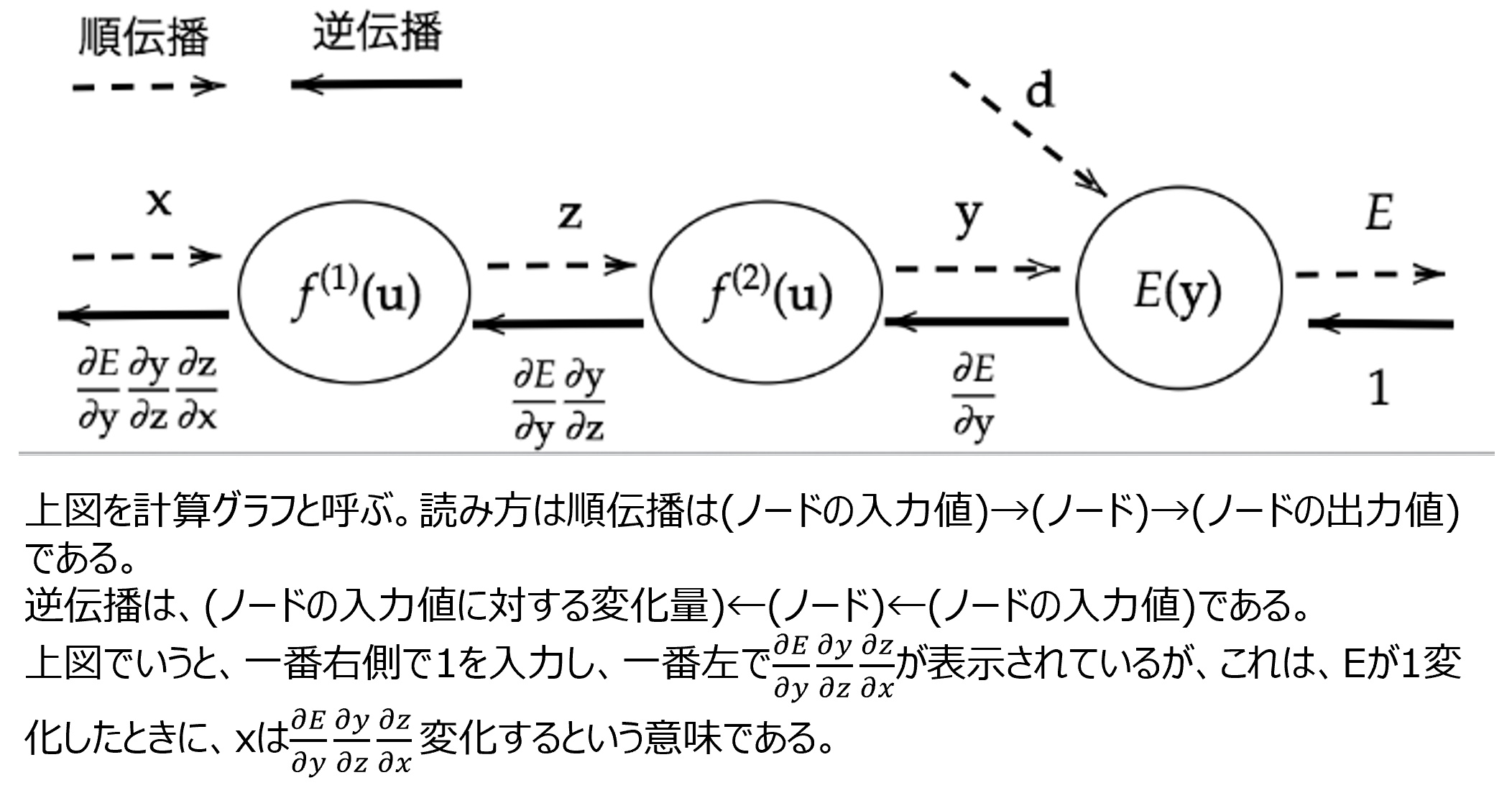
確認テスト
- 誤差逆伝播法では不要な再帰的処理を避けることができる。既に行った計算結果を保持しているソースコード抽出せよ。
delta2 = functions.d_mean_squared_error(d, y)
- 2つの空欄に該当するソースコードを探せ
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
grad['W1'] = np.dot(x.T, delta1)
ハンズオン
ハンズオン結果は下記。Section4のスクリプトにSection5も含まれているので、Section4と同じ。
ハンズオン
参考文献
本レポート内容は全てニューラルネットワークの基礎であるから、全てのセクションにおいて共通の参考図書を挙げる。
まず最初に挙げる参考図書は、ニューラルネットワーク情報処理。本書は、ニューラルネットワークの歴史から説明されており、導入は読み物としても楽しめた。その一方で、数式に関する説明はかなり行間を読む必要があり、最初はちんぷんかんぷんであった。
次に挙げるのはゼロから作るDeep Learningである。本書を読むまではニューラルネットワークを使うときに、理論に対してはなんとなくの理解でライブラリを使っていた。しかし、本書を読むことで理論の基本は理解できたし、演習としてスクラッチ開発をすることで、ライブラリでは対応できないニューラルネットワークも作成できるようになった。