HEROZの社内勉強会でコンピュータービジョンの基礎について調査し発表したので、その内容をまとめます。
参考文献:
主に前者の「実践コンピュータビジョン(PCVP)」の1章から5章の演習ノート的な内容となっています。
- PCVPの説明は厳密でない場合があるので、気になった部分について別の資料(特に後者のMVGCV)を参照し説明を追加しました。ただ、MVGCVはつまみ読みしかしていないので説明が間違っている箇所もあるかもしれません。
- PCVPのサンプルコードについては、numpyでスクラッチで書かれている部分も多いですが、それがOpen CVのどのライブラリに相当するかについて分かる範囲で記しました。
- この本は深層学習は扱っていないので、物体の数え上げや画像の分類、検索といった(現時点で)深層学習が得意そうなタスクについての内容については飛ばしました。
- 自分のメモや発表資料からコピペしたので、ですます調とである調が混ざっている点についてはご容赦ください
またこの記事中の画像の一部は "Programming Computer Vision with Python" by Jan Erik Solem (O'Reilly Media, 2012).のデータから引用・加工したものとなっています。
基本的な画像処理
(PCVP 1章参照)
画像の微分
(PCVP 1.4.2参照)
コンピュータービジョンにおいては明度の勾配が重要になる。それを計算するために、画像の微分を計算する必要がある。
例えばx方向のSobelフィルタは次のように表せる。
\begin{pmatrix}
-1 & 0 & 1 \\
-2 & 0 & 2 \\
-1 & 0 & 1
\end{pmatrix}
x方向、y方向微分を用いて、勾配が計算できる。勾配の大きさを図示すると次のようになる。

画像の局所記述子
(PCVP 2章参照)
画像中の点同士の対応を発見するために、画像中の特徴的な点を抽出するということが行われます。
この章の画像の特徴点・記述子については、@icoxfog417さんがかなり詳しく解説しているので、詳しくは以下を参照してください
画像処理の数式を見て石になった時のための、金の針 - Qiit
以下ではその計算方法の概要を説明します。
Harrisコーナー記述子
(PCVP 2.1参照)
画像のある点において、$I_x$、$I_y$をそれぞれx方向の微分、y方向の微分として次のような行列$M_I$を考える
M_I=\begin{pmatrix}
I_x^2 & I_xI_y \\
I_xI_y & I_y^2
\end{pmatrix}
周辺ピクセルの影響も考えるため、ガウスフィルター$W$を畳み込む
M=W*M_I
いきなり$M_I$と$M$という行列が出てきたが、次に簡単に説明する通り、実はこの$M$の2つの固有値の大きさでコーナーを検出できる。
コーナーの性質
明度$I(x,y)$が直交する2つの方向に移動したときに大きく変化する場所をコーナーと考える。この性質は実は行列の対角化で表現することができる。
明度の変化は次のように表せる
E(u,v)=\sum_{x,y}{w(x,y)[I(x+u,y+v)-I(x,y)]^2}
テイラー展開
テイラー展開によって2次元関数は次のように近似できる。$u$、$v$は微少だとする。
f(x+u,y+v)=f(x,y)+uf_x+vf_y
これを上に用いれば
\begin{align}
[I(x+u,y+v)-I(x,y)]^2
&=[uI_x+vI_y]^2\\
&=u^2I_x^2+2uvI_xI_y+v^2I_y^2\\
&=
\begin{pmatrix}
u&v
\end{pmatrix}
\begin{pmatrix}
I_x^2 & I_xI_y \\
I_xI_y & I_y^2
\end{pmatrix}
\begin{pmatrix}
u\\v
\end{pmatrix}\\
&=
\begin{pmatrix}
u&v
\end{pmatrix}
M_I
\begin{pmatrix}
u\\v
\end{pmatrix}
\end{align}
二次形式
↑の議論から若干飛躍してしまうが、明度変化$E$は次のように表せる。$M_I$にガウスフィルターを畳み込んでできた$M$も$M_I$と似たような行列と考えてよくて、対称行列となる。そして明度変化は$M$を用いて次のように表せる。
E(u,v)=\begin{pmatrix}
u&v
\end{pmatrix}
M
\begin{pmatrix}
u\\v
\end{pmatrix}
これは二次形式である。二次形式についてはここを参照
二次形式の意味,微分,標準形など
↑のサイトにも書いてある通り、対称行列は直交行列で対角化可能である。つまり$M$は直交行列$U$で
UMU^T=
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2 \\
\end{pmatrix}
と2つの固有値が対角に並んだ行列に対角化できる。
つまり$\boldsymbol{x}=(u\ v)$で、$\boldsymbol{X}=U\boldsymbol{x}$と座標変換すると、
\begin{align}
\boldsymbol{x}^TM\boldsymbol{x}&=
\boldsymbol{X}^T
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2 \\
\end{pmatrix}
\boldsymbol{X}\\
&=\sum_i{\lambda_iX_i^2}
\end{align}
Harrisコーナー検出
つまり、元の座標から、$\boldsymbol{X}=U\boldsymbol{x}$と座標変換すれば、明度変化$E$は次のようになる。
E(u,v)=\sum_i{\lambda_iX_i^2}
これは$X_1$という方向に離れると$\lambda_1$だけ、そしてそれと直交する方向$X_2$という方向に離れると$\lambda_2$だけ明度が変化することを表す。
よって2つの固有値$\lambda_1$と$\lambda_2$がどちらも大きい場合にコーナーと判断する。このように行列の対角化によってコーナーの性質が表せた。
画像のマッチング
このHarrisコーナー検出とPCVP 2.1.1に述べられている正規化相互相関を用いれば、以下のように画像のマッチングができる。

ライブラリの利用
以上の画像のマッチングはOpen CVを用いればより簡単にできる。
SIFT
SIFTは特許で保護されていたので、デフォルトのOpen CVには含まれておらず、追加パッケージをインストールする必要があったが、2021年3月に期限切れになったので、普通に使えるようになった。
SIFTの特許が切れてOpenCV v4.4.0から普通に使えるようになってた話 - Qiita
PCVPではKeypoint detectorからバイナリを入手し、コマンド実行で使用しているが、OpenCVのSIFTを用いた方が楽。
以下の記事を参考。
AKAZE
SIFTより性能がいいらしい、AKAZEというものもあるらしい。
以下の記事を参考。
OpenCV - 特徴点マッチングを行う方法について - pystyle
画像間の写像
(PCVP 3章参照)
同次座標
2次元座標上の点は$(x,y)$と2つの数の組で表せるが、もう1つ座標を加えて、$(x,y,1)$として表す。このような座標のことを同次座標(homogeneous coordinate)と呼ぶ
アフィン変換・ホモグラフィ変換
座標$(x,y)$を座標$(x',y')$に次のように変換するとき、線形変換と呼ぶ。
\begin{pmatrix}
x' \\
y'
\end{pmatrix}=
\begin{pmatrix}
a_1 & a_2 \\
a_3 & a_4
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
拡大、縮小、回転、せん断といった変形は線形変換で表せる

一方平行移動は次のように表せる。
\begin{cases}
x' = x+t_x \\
y' = y+t_y
\end{cases}
2次元座標を3つの値で表す同次座標で表せば、拡大、縮小、回転、せん断に加え平行移動も行列で表せる(アフィン変換)
同次座標を用いればこれを行列の積で表すことができる。
\begin{pmatrix}
x' \\
y' \\
1
\end{pmatrix}=
\begin{pmatrix}
a_1 & a_2 & t_x \\
a_3 & a_4 & t_y \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
アフィン変換は2x3だが、3x3すべて使うと、より一般的な変換を表せる。これをホモグラフィ変換と呼ぶ。
\begin{pmatrix}
x' \\
y' \\
w'
\end{pmatrix}=
\begin{pmatrix}
h_1 & h_2 & h_3 \\
h_4 & h_5 & h_6 \\
h_7 & h_8 & h_9
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
w
\end{pmatrix}

同次座標、アフィン変換、射影変換について詳しくは以下を参照
射影平面について
(MVGCV 1.1、2.2参照)
さきほど導入した2次元座標を3つの値で表す同次座標は、定数倍しても同じ点を表します。また、最後の1を取れば、元の2次元座標に戻せるという性質があります。一般的な平面はユークリッド平面、同次座標で表す平面は射影平面と言います。射影平面は次のように図示できます。
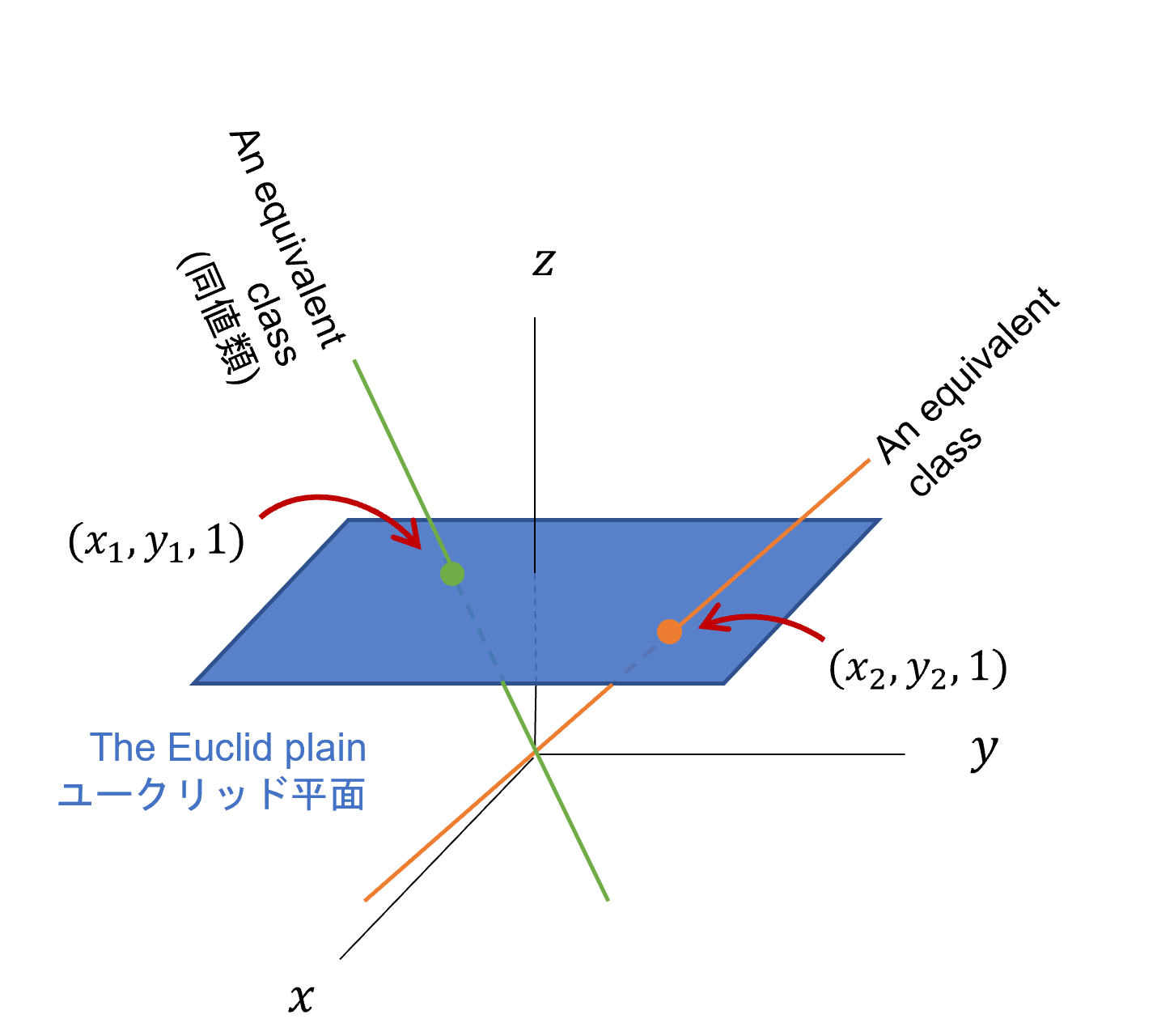
定数倍しても同じ点を表すので、原点を通る直線が1つの点を表す同値類だといえます。そしてその直線とz=1の平面の交点が、元のユークリッド平面の座標と言えます。つまり、射影平面をこの方法で図示すると、点は直線として表せます。そして同様にユークリッド平面上での直線は原点を通る平面として表せます。それをユークリッド平面へ戻す場合は$z=1$平面との交線が、元の平面だと考えればいいです。
| ユークリッド平面 | 「射影平面の図示」での見え方 | 「射影平面の図示」からユークリッド平面への戻し方 |
|---|---|---|
| 点 | 原点を通る直線 | 原点を通る直線と$z=1$平面との交点 |
| 直線 | 原点を通る平面 | 原点を通る平面と$z=1$平面との交線 |
また同様に、3次元空間上の点を4つの値で表すと、3次元射影空間になります。
射影空間の図示について詳しくは私が以前まとめた次の記事を参照してください。
射影平面での点と線
(MVGCV 2.2参照)
ご存知のように傾き$a'$とy切片$b'$の直線は$y=a'x+b'$という式で表せます。別の書き方として、$ax+by+c=0$としてもこの式を満たす点$\boldsymbol{x}=(x,y)^T$の集合は直線を表します。また、同次座標では$\boldsymbol{x}$を$(x,y,1)^T$と表すので、$\boldsymbol{l}=(a,b.c)^T$とすれば、ある直線上の点は$\boldsymbol{x}^T\boldsymbol{l}=0$を満たします。そこで射影平面では直線を表すのに$\boldsymbol{l}=(a,b.c)^T$と表します。上で述べたように直線を「射影平面の図示」で見ると、原点を通る平面に見えますが、$\boldsymbol{l}=(a,b,c)^T$はその平面に垂直方向のベクトルだとも解釈できます。
この表し方をすると、2つの直線$\boldsymbol{l}$、$\boldsymbol{l}'$の交点は$\boldsymbol{l}\times\boldsymbol{l}'$となることが導けます。一方2つの点$\boldsymbol{x}$、$\boldsymbol{x}'$を通る直線は$\boldsymbol{x}\times\boldsymbol{x}'$と表せることも導けます。
このように、射影平面ではどの理論も点と直線を入れ替えることで、双対な理論と対応付けることができます。これを双対原理と呼びます。
DLTアルゴリズム
(PCVP 3.1.1参照)
上記したように、ある点$x$をホモグラフィ行列$H$を用いて点$x'$へホモグラフィ変換する式は次のようになる。
\boldsymbol{x}'=H\boldsymbol{x}
このある点$\boldsymbol{x}$から$\boldsymbol{x}'$へ変換する$H$を求めるのがDirect Linear Transformation(DLT)アルゴリズムである。
PCVP 3.1.1にあるように、DLTアルゴリズムは$\boldsymbol{x}$と$\boldsymbol{x}'$の要素から計算できる$A$という行列とホモグラフィ行列$H$の要素が次の式を満たすことを利用する。
A\begin{pmatrix}
h_1 \\ h_2 \\ h_3 \\
h_4 \\ h_5 \\ h_6 \\
h_7 \\ h_8 \\ h_9
\end{pmatrix}=0
この$A$を次のように特異値分解したときの右特異行列の8行目を$3\times3$に整形した行列がホモグラフィ行列$H$の推定値となる。

詳しい導出はMVGCVの4.1(p88)を参照。また途中で出てくる$A$のランクと$h$の次元の関係については以下の記事参照。
線形写像の次元定理dim V = rank f + dim ker fの証明 | 数学の景色
特異値分解については、MVGCVのA.5(p588)や日本語の場合次の資料を参照。
ライブラリの利用
以上の画像の変換や、変換行列の推定はOpen CVを用いればより簡単にできる。
-
cv2.getAffinTransform:3つの点の対応からアフィン変換を求める -
cv2.warpAffine:アフィン変換を画像に適用 -
cv2.getPerspectiveTransform:4つの点の対応から射影変換を求める -
cv2.findHomography:5つ以上の点の対応から最適な射影変換を推定する -
cv2.warpPerspective:射影変換を画像に適用
詳しい使い方は以下参照
応用:パノラマ写真
上記を応用することで、撮影する時にオーバーラップさせた2枚の写真について、特徴点マッチングからホモグラフィー行列を推定し、パノラマ写真を作成することができる。



カメラモデルと拡張現実
(PCVP 4章参照)
カメラ座標系→画像座標系
3次元上の座標から、画像中の2次元座標への変換を考える。ズーム倍率を指定すれば、多くのカメラはピンホールカメラとしてモデル化できる。ピンホールカメラでは穴の位置から造影素子の距離を焦点距離を$f$ピクセルとする。

原点をピンホールの穴、z軸をカメラ前方向、y軸を下向きにした座標系で考えて、さらに原点の後ろの撮像素子を前に持ってくると次のような関係になっている。
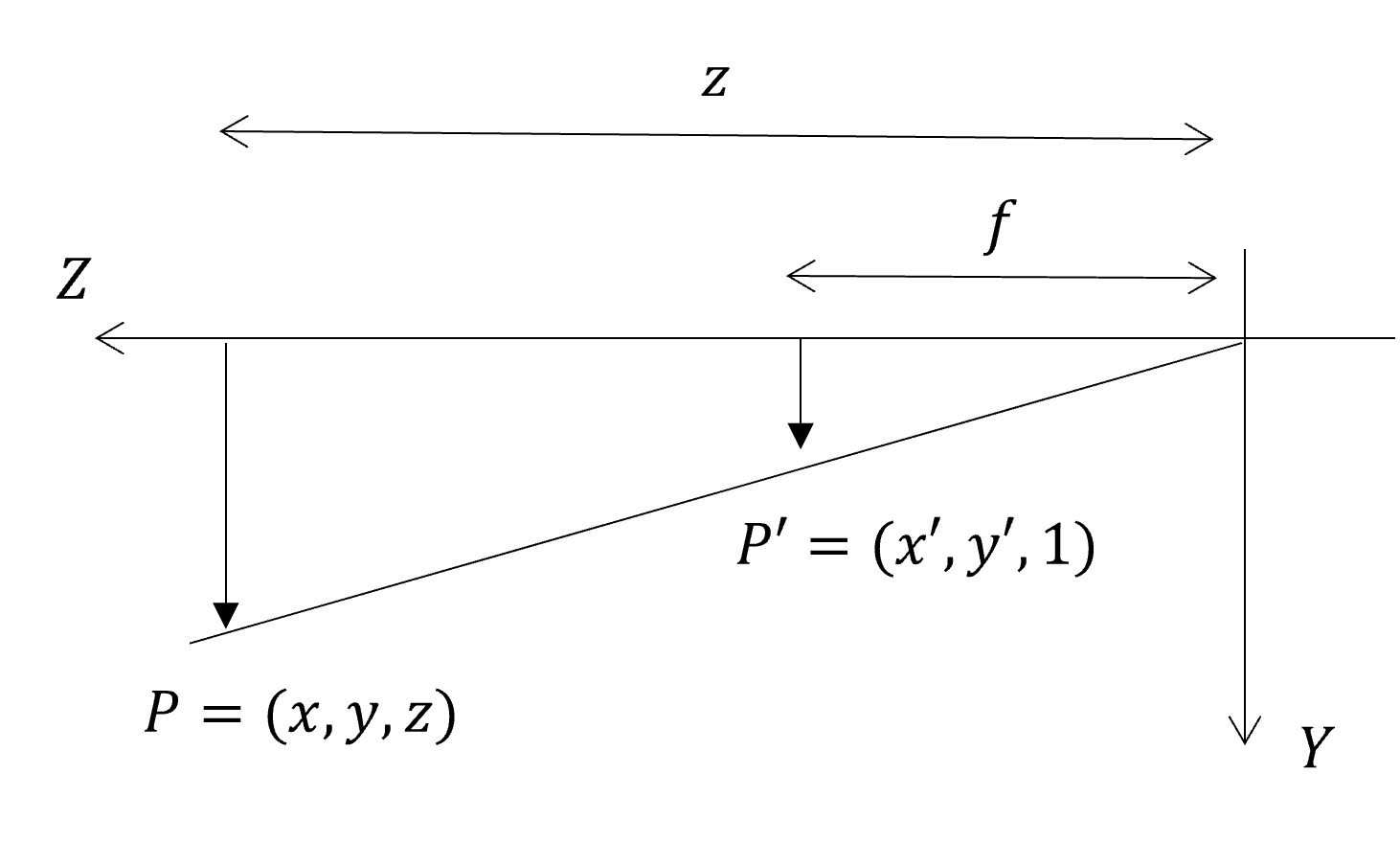
三角形の相似の関係から、被写体のある点は撮像素子上の座標は次のような式で表せる。
\begin{cases}
x' = f\frac{x}{z} \\
y' = f\frac{y}{z}
\end{cases}
これを、より詳細に考察すると、カメラ中心を原点としたカメラ座標系の3次元上の点から、画像上の座標系への変換できる。
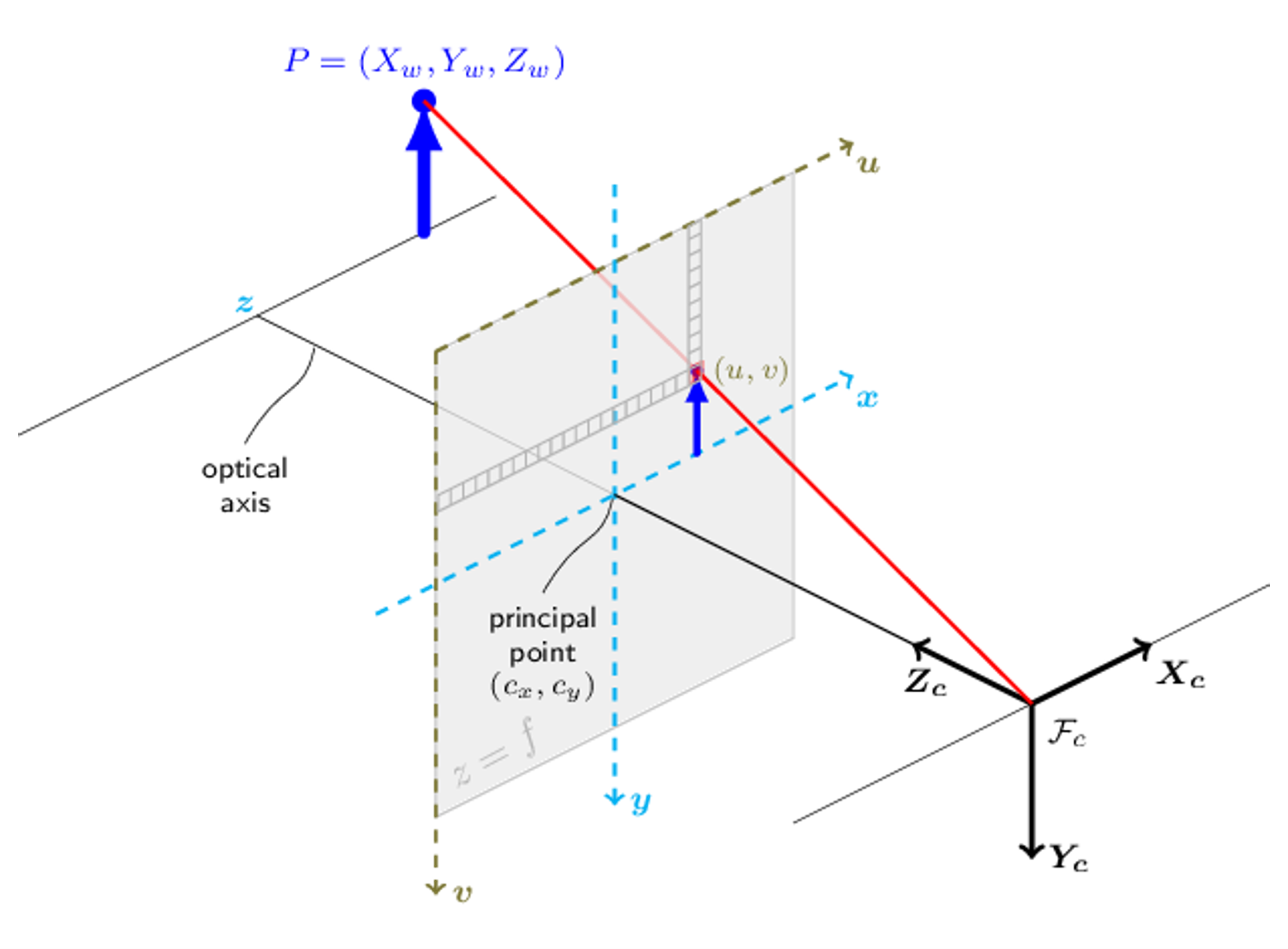
(https://docs.opencv.org/3.4/d9/d0c/group__calib3d.htmlからの画像)
そしてカメラ座標系→画像座標系の変換は同次座標を用いて次のように表せる。
\lambda
\begin{pmatrix}
u \\
v \\
1
\end{pmatrix}
=\begin{pmatrix}
f & 0 & c_x\\
0 & f & c_y\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}
=K\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}
このとき$K$はキャリブレーション行列と呼ばれる。このように、3次元上の座標から、画像上の2次元ピクセル座標の同次座標が1つの行列計算で求められる。
ここで$\lambda=z$であるが、同次座標はその定義から定数倍しても同じ座標を表すので、左についている$\lambda$は気にしなくてもいい。
ワールド座標系→カメラ座標系
3次元座標上での座標変換は、2次元座標系でのアフィン変換と同様、3次元座標を同次座標で表すことで、平行移動と回転移動を一つの行列計算で表せる。つまり任意の点を原点とした、ワールド座標系からカメラ座標系への変換は次のように表せる。
\begin{pmatrix}
x_c \\
y_c \\
z_c
\end{pmatrix}
=R\begin{pmatrix}
x_w \\
y_w \\
z_w
\end{pmatrix}
+\begin{pmatrix}
t_x \\
t_y \\
t_z
\end{pmatrix}=
\left(R|t\right)\begin{pmatrix}
x_w \\
y_w \\
z_w \\
1
\end{pmatrix}
ここで$R$はワールド座標系→カメラ座標系の座標変換の回転、$t$はワールド座標系→カメラ座標系の座標変換の平行移動である。
ワールド座標系→画像座標系
ワールド座標系→カメラ座標系→画像座標系の2つの変換をまとめると、 ワールド座標系→画像座標系への変換は次のようになる。
\lambda
\begin{pmatrix}
u \\
v \\
1
\end{pmatrix}=
K\left(R|t\right)
\begin{pmatrix}
x_w \\
y_w \\
z_w \\
1
\end{pmatrix}
=P\begin{pmatrix}
x_w \\
y_w \\
z_w \\
1
\end{pmatrix}
ここで$P$はカメラ行列と呼ばれる。
ピンホールカメラモデルについて詳しくは以下を参照
拡張現実
(PCVP 4.2参照)
カメラの焦点距離を計測し、キャリブレーション行列を計算し、さらに特徴点マッチングとホモグラフィー行列の推定とあわせれば、拡張現実的なことができる

ホモグラフィー行列を推定し、カメラ行列を計算し、マーカー上の座標から、画像座標系へ立方体を射影することができる。

多視点幾何学
PCVP 5章参照(ですがこの章のPCVPの説明はかなりざっくりしています)
エピポーラ幾何
同じ点$X$を2台のカメラで撮影したときの幾何を考えます。
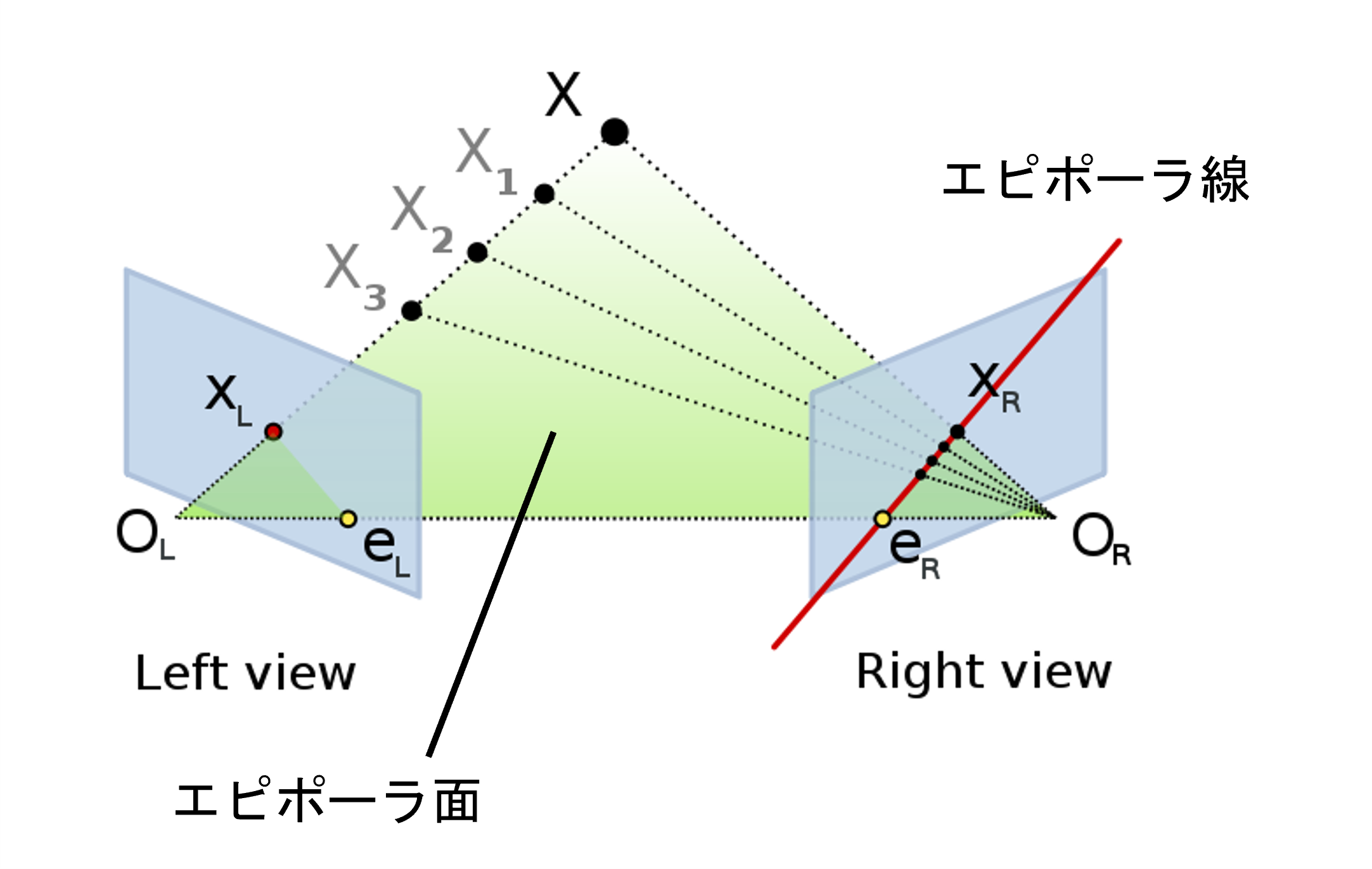
(Arne Nordmannによる図を編集)
ここの説明については@Thought_Nibblerさんの記事が大変分かりやすかったので引用させていただきます。
「カメラ $O_L$ から見ると $X_L$ に物体が写っている」ことしか分かっていない時点では、 $X, X_1, X_2, X_3$ のどこに物体があるかわからない。「カメラ $O_R$ から見て $X_R$ に同じ物体が写っている」ことも分かった場合は、 $X$ に物体があると特定できる。
エピポーラ線(Epiline) : 図の赤線
- 「カメラ $O_L$ から見て $X_L$ に物体が写っている」とき、「カメラ $O_R$ から見てどこに物体が写るか」の候補
エピポール(Epipole) : 図の点 $e_L, e_R$
- 一方のカメラから他方のカメラが写る位置のこと
- 物体の位置に関係なく一定
- どの物体のエピポーラ線もエピポールで交わる
エピポーラ面(Epipolar Plane) : 図の緑面 $O_L X O_R$
- 物体の位置と2つのカメラ位置の3点で決まる平面
- エピポーラ線・エピポールはエピポーラ面上にある
エピポーラ拘束
PCVPやMVGCVと記号を合わせるため、もう一度同じ図を示します。

同じ点$X$を映した$\boldsymbol{x}$と$\boldsymbol{x}'$、そしてそれぞれのカメラ行列$P$と$P'$の間には何らかの制約条件があるはずです。それがエピポーラ拘束と呼ばれます。
それは次のような式で表せます。
\boldsymbol{x}'^T\boldsymbol{l}'=\boldsymbol{x}'^TF\boldsymbol{x}=0
$\boldsymbol{l}'$は先ほど出てきた射影平面での直線の表し方で、エピポーラ線を表します。$F$は基礎行列と呼ばれます。
エピポーラ線$\boldsymbol{l}'$の表し方はいくつかあり、MVGCVでは
\boldsymbol{l}'=\boldsymbol{e}'\times\boldsymbol{x}'
あるいは
\boldsymbol{l}'=P'C\times P'P^+x
と表しています。
$F$の表し方もいくつかあるのですが、世界座標の原点が1番目のカメラの中心にあるとする場合、次のように表せます。(PCVPのp104の5.1式)
F=K_2^{-T}S_tRK_1^{-1}
この式の導出はMVGCV 9.2 (p241)を参照すれば分かります。
基本行列の性質
(MVGCV 9.2.4参照)
- 転置:$P,P'$に対する基本行列が$F$なら、$P',P$に対する基本行列は$F^T$である
- エピポール点:画像1でのカメラ2の座標$e$について、全ての$x'$に対し、$x'Fe=0$なので、$Fe=0$である。つまり$e$は$F$の核である。
多視点による復元
(PCVP 5.3参照)
上記を応用することで、2枚の画像中の点についてその3次元座標を計算できる。
キャリブレーション行列$K_1、K_2$は既知だとし、世界座標の原点がカメラ1の中心だとすると
- 世界座標の原点がカメラ1の中心なので$P_1$は既知
- 特徴点同士の対応で$F$が計算できる。
- $F$から$P_2$が計算できる。
- $P_1,P_2$から$X$が計算できる
応用
SfM
何段階か拡張することで、多視点からの3D復元が可能となる。SfM(Structure from Motion、運動からの構造復元)と呼ばれ、多数の画像、動画から対象物の3次元座標を復元する。
SLAM
ロボットの自律制御にもコンピュータービジョンは用いられる。SLAM(Simultaneous Localization and Mapping, 自己位置推定とマッピングの同時実行)では画像を用いた特徴点マッチングによる自己位置推定とマッピングを用いるものもある(visual SLAM)
感想
まだまだ説明不足・勉強不足な部分がありますが、とりあえずここまでとします。

