最適化について一般的なことを説明し、その中でも勾配降下法なども説明しつつ、ガウス・ニュートン法の導出について簡単に説明する。ガウス・ニュートン法によるモデルのパラメータ推定についても説明し、具体的な問題に適用した場合も実演する。
この記事を書いた動機
書籍やネット上で最適化についての資料はたくさんあるが、ガウス・ニュートン法についてもっと簡単に説明できないかと思ったため。
間違い等あれば指摘お願いいたします。
最適化とは
最適化とはいろいろな制約の中で、複数の選択肢から最適なものを選ぶことである。
最適化は様々な分野で用いられる。
- 企業の経営戦略:どの事業に投資すれば売り上げ、利益を最大化できるか?
- 設計:強度があって軽い製品にするための材料はどうするべきか?
- 生産計画:限られた時間とコストの中で、できるだけ多くの製品を作りたい
- 制御:システムが目的通りの挙動するように最適化する
- モデル化:現実の現象を最もよく表すモデルのパラメータは何か?
- 機械学習:目的関数を最小化するモデルのパラメータは何か?
最適化問題
これら最適化問題について数学的に考えてみる。
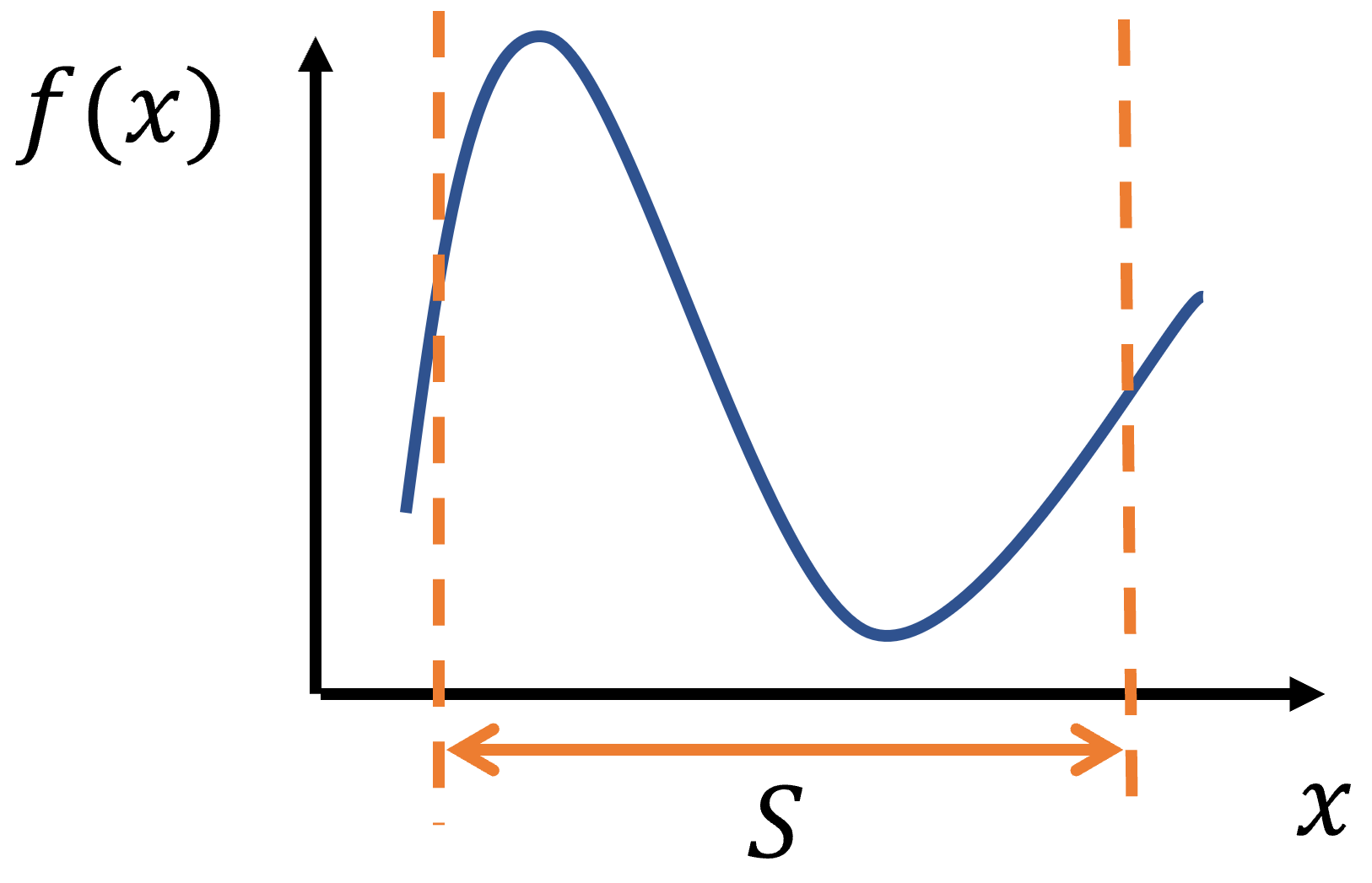
ある変数$x$がある範囲$S$の中で動くとき、$x$についての関数$f(x)$を最小化する$x$を探索する問題は
\begin{align}
f(x)\rightarrow min\\
x\in S
\end{align}
と書ける。$x$を「決定変数」、$f(x)$を目的の達成度を表す「目的関数」、決定変数に課される条件$S$を「制約条件」と呼ぶ。変数が1次元の時の場合のイメージを図にした。
最適化問題の種類
最適化問題はいろいろな種類の問題があり、分類の方法もいろいろある。詳しくはWikipediaの最適化問題のページを参照
決定変数について分類
- 連続最適化問題:連続的な値を取る場合
- 離散最適化問題:0か1、離散的な値を取る場合
目的関数についての分類
- 線形計画問題:目的関数が線形関数
- 非線形計画問題:目的関数が線形でない
最適化問題の解法の種類
またその最適化問題を解く手法(アルゴリズム)にも様々な種類がある。
導関数を使うアルゴリズム
- 最急降下法(勾配降下法)
- ニュートン法
- 準ニュートン法
- ガウス・ニュートン法(最小二乗法でパラメータを求める場合)
導関数を使わないアルゴリズム
- アニーリング法
- タブー探索法
- 遺伝アルゴリズム
- 粒子群最適法
- ベイズ最適化
各アルゴリズムのPythonライブラリ
有名なアルゴリズムについてはPythonのモジュールやサンプルコードあるので自分で実装する必要はないが、そのアルゴリズムについて基礎的なことは理解していた方がいい。
- ガウス・ニュートン法(に似た、より効率の良いアルゴリズム):scipy.optimize.least_squares
- 遺伝アルゴリズム:DEAP
- ベイズ最適化:GpyOpt
ガウス・ニュートン法の導出
ここから各種最適化アルゴリズムの中でも、導関数を使った最適化の1つであるガウス・ニュートン法を導出し、その後ガウス・ニュートン法を使ったモデルのパラメータ推定について実験してみる。
ガウス・ニュートン法はある現象をパラメータを含んだモデル関数によってモデル化するとき、効率的にパラメータの探索するアルゴリズムである。
ここからその手法を導出していく。本来は、最適化問題についてはもっと厳密な議論が必要だが、今回はイメージ優先で厳密な議論はしない。正確な議論を知りたい場合は参考文献や論文など参照してほしい。
1変数関数の最小化
まず、1変数関数の最小化について説明する。
最急降下法
まずもっとも単純な最急降下法(勾配降下法)について述べる。

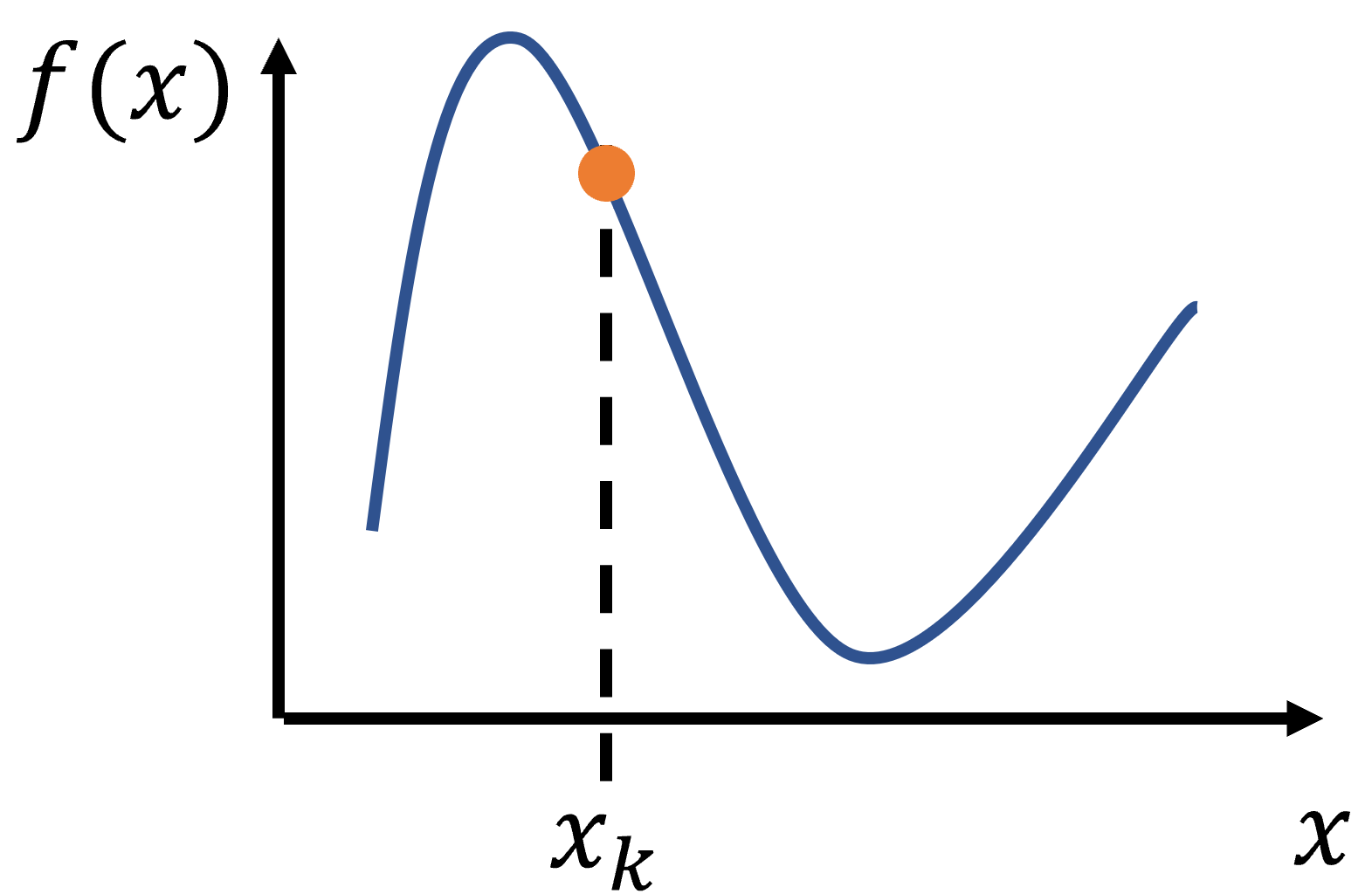
まず上図のような関数$f(x)$があったとする。
- 反復数のカウンターを$k=0$とする。下図のように初期値を$x_0$とし適当に置く。
-
以下3~4を反復する。
-
$x_k$での勾配$f'(x_k)$を計算する
-
下図のように$x_{k+1}=x_k-\alpha f'(x_k)$と更新する。
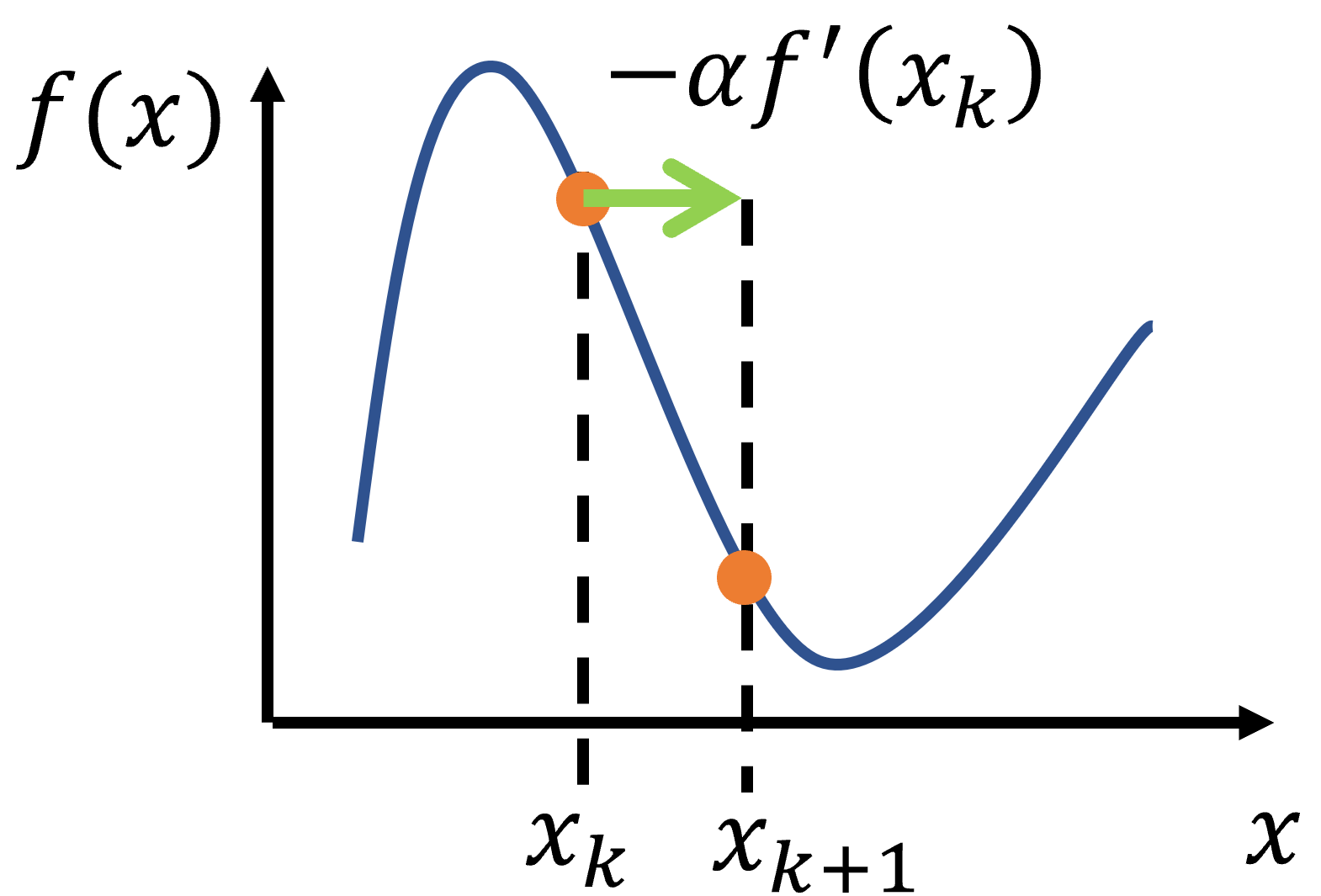
- $||f'(x_k)||$が十分小さくなるまで続ける。
$\alpha$は更新の度合いを決めるパラメータである。
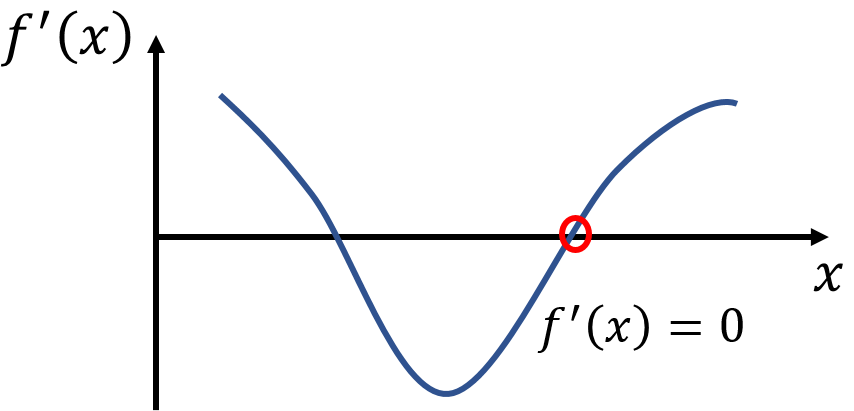
ここで、効率的に最小値を求める方法を考える。最小値ではないかもしれないが、少なくとも$f(x)$が極小値となる点を探す。それはつまり下図のように$f(x)$の微分が0、つまり
f'(x)=0
となる$x$が分かればいい。
そこで、4で$x_{k+1}$を求める際に、$f'(x_{k+1})$が0に近くなるようにαを定めると、効率的に最小値を求められる。つまり$f'(x_{k+1})=0$という式を解くことになる。
一般に$g(y)=0$を解くことを方程式を解くという。数値的に(数値的:プログラムで計算して)方程式を解く方法として、ニュートン法というものがある。つまり最急降下法はニュートン法を用いることで、効率的に最小値が求められるようになる。
ニュートン法
ここで数値的に方程式を解くニュートン法を、下図のような関数$g(y)$について、$g(y)=0$を解いてみて説明する。

1.$y_0$を適当に置く
2.以下3~4を繰り返す
3.y_kの曲線上での接線を求める
4.その接線と横軸との交点を求めて$y_{k+1}$とする

接線は2点$(y_k,g(y_k))$、$(y_{k+1},0)$を通り、その傾きは$g(y_k)/(y_k-y_{k+1})$と表せられる。また同時に点$y_k$の微分$g'(y_k)$もその点での接線の傾きなので、$g(y_k)/(y_k-y_{k+1})=g'(y_k)$となる。よって$y_{k+1}$を求めるには、
y_{k+1}=y_k-\frac{g(y_k)}{g'(y_k)}
を計算すればいい。これを反復し、$g(y_d)=0$となる$y_d$を探索する。
最急降下法にニュートン法を用いる
ここまでを振り返ってみると、
勾配法では、
x_{k+1}=x_k-\alpha f'(x_k)
と$x_{k+1}$を更新する。
$f'(x)=0$となる$x$を探せば効率的に最小値が探索できる。
また、$\alpha$は更新の度合いを決めるパラメータで自由に決められる。
ニュートン法では、
$g(y)=0$となる$y$を探す
y_{k+1}=y_k-\frac{g(y_k)}{g'(y_k)}
と$y_{k+1}$を更新する。
この式を見比べれば、$g(y)$にあたるものが$f'(x)$なので、$g'(y)$にあたるものは$f''(x)$である。よって効率的に最小値を探索するには、$\alpha=1/f''(x_k)$とし、
x_{k+1}=x_k- \frac{f'(x_k)}{f''(x_k)}
と$x_k$を更新すれば$f'(x)=0$となる$x$を探せ、効率的に最小値が探索できることが分かる。(しかしこれでは極小値ではなく極大値を探索してしまう可能性もあるが、それについては無視することとする。)
多変数関数の最小化
今まで、1変数関数の最小化を考えてきたが、ここでは多変数関数の最小化について考える。多変数関数の場合、決定変数は$(x_1,x_2,\cdots)$と複数の変数を持つことになり、最適化する関数も$f(x_1,x_2,\cdots)$と複数の値に対し、値を返す多変数関数となる。複数の変数をまとめて決定変数ベクトル$\pmb{x}=(x_1,x_2,\cdots)$と書く。最適化問題は
\begin{align}
f(\pmb{x})\rightarrow \min \\
\pmb{x}\in S
\end{align}
となる。
多変数関数の最急降下法
1変数関数の最急降下法の場合
x_{k+1}=x_k-\alpha f'(x_k)
を繰り返し、その時に
f'(x)=0
となる$x$が分かれば効率的に最小化できたのであった。
多変数関数を最急降下法で最小化する場合も、同様に
\pmb{x}_{k+1}=\pmb{x}_k-\alpha \nabla f(\pmb{x}_k)
を繰り返し、その時に
\nabla f(\pmb{x})=0
となる$\pmb{x}$が分かれば効率的に最小化できる。ただし$\nabla f(\pmb{x})$は$\pmb{x}$に関する$f(\pmb{x})$の勾配ベクトルである。勾配ベクトルは$f(\pmb{x})$を$x_1,x_2,\cdots$のそれぞれで偏微分したベクトルで、
\nabla f(\pmb{x})=\left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots\right)^T
と表せる。
多変数ベクトル値関数のニュートン法
多変数関数の最急降下法を効率的に行うために、
\nabla f(\pmb{x})=0
を解く必要がある。この$\nabla f(\pmb{x})$は複数の変数を持ち、複数の値を返す、多変数ベクトル値関数なので、多変数ベクトル値関数に関するニュートン法について考えなければならない。
多変数ベクトル値関数を$\pmb{g}(\pmb{y})$とすると、その全ての値が$0$、つまり、
\begin{align}
\pmb{g}(\pmb{y})&=(g_1(y_1,y_2,...),g_2(y_1,y_2,...),...)^T\\
&=(0,0,...)^T
\end{align}
\tag{1}
を数値的に解く場合について考える。
前に述べたように1変数関数のニュートン法の場合、
y_{k+1}=y_k-\frac{g(y_k)}{g'(y_k)}
を繰り返せばよかったから、多変数ベクトル値関数の場合も、正確ではないが、気持ちとしては
\pmb{y}_{k+1}=\pmb{y}_k-\frac{\pmb{g}(\pmb{y}_k)}{\pmb{g}'(\pmb{y}_k)}
を繰り返せばいいと考えられる。
実際、正確には、
\nabla \pmb{g}(\pmb{y}_k)\Delta\pmb{y}_k=-\pmb{g}(\pmb{y}_k) \tag{2}
を満たす$\Delta\pmb{y}_k$を計算し、そして、
\pmb{y}_{k+1}=\pmb{y}_k+\Delta\pmb{y}_k
を計算し、これを反復すれば式(1)を満たす$\pmb{y}$を見つけられる。
ただし、ここで$\nabla \pmb{g}(\pmb{y})$はベクトル$\pmb{y}$に対する$\pmb{g}(\pmb{y})$の勾配行列で
\nabla \pmb{g}(\pmb{y})=
\begin{pmatrix}
\frac{\partial g_1}{\partial y_1} & \frac{\partial g_1}{\partial y_2} & \cdots \\
\frac{\partial g_2}{\partial y_1} & \cdots & \cdots\\
\cdots & \cdots & \cdots
\end{pmatrix}
である。さきほどの$\nabla f(\pmb{x})$については、$f(\pmb{x})$が多変数に対する1値関数だったので、$\nabla f(\pmb{x})$は勾配ベクトルとなったが、$\pmb{g}(\pmb{y})$は多変数ベクトル値関数なので、$\nabla \pmb{g}(\pmb{y})$は勾配行列となる。
一般的に、式(2)を解くことは、線形連立方程式を解くことになり、$LU$分解などの連立方程式を数値的に解くアルゴリズムが使える。
多変数関数の最急降下法にニュートン法を用いる
1変数関数と同様に考えて、$\pmb{g}(\pmb{y})$にあたるものが$\nabla f(\pmb{x})$なので、
\nabla^2 f(\pmb{x}_k)\Delta\pmb{x}=-\nabla f(\pmb{x}_k)
を満たす$\Delta\pmb{x}$を用いて、
\pmb{x}_{k+1}=\pmb{x}_k+\Delta\pmb{x}_k
と更新することを繰り返せば、$f(\pmb{x})$を最小化する$\pmb{x}$を見つけることができる。(ここでも極小値ではなく極大値を探索してしまう可能性もあるが、それについては無視することとする。)
ただし、ここで$\nabla^2 f(\pmb{x})$はベクトル$\pmb{x}$に対する$\pmb{f}(\pmb{x})$の2回微分の行列でヘッシアン$H$といい、
\begin{align}
\nabla^2 f(\pmb{x})&=H\\
&=
\begin{pmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\partial x_2} & \cdots \\
\frac{\partial f}{\partial x_2\partial x_1} & \cdots & \cdots\\
\cdots & \cdots & \cdots
\end{pmatrix}
\end{align}
である。
テイラー展開を用いた多変数関数の最小化
今まで述べた多変数関数の最適化について、テイラー展開を用いて説明することもできる。数理最適化の教科書はこの説明を使うことが多い。
放物線の最小化
まず、下に凸な放物線の式($a>0$)
g(x)=\frac{a}{2}x^2+bx+c\tag{3}
を最小化する$x$は、この式を平方完成し、軸の位置を求めることで求まる。
\begin{align}
g(x)&=\frac{a}{2}x^2+bx+c\\
&=\frac{a}{2}\left(x+\frac{b}{a}\right)^2+c-\frac{b^2}{2a}
\end{align}
よって$g(x)$は$x=-b/a$で最小となる。後の為に少し式変形すると
ax=-b\tag{4}
を満たす$x$で$g(x)$は最小になるとも言える。
テイラー展開を用いた多変数関数の最小化
多変数関数$f(\pmb{x})$を最小化したいとする。
\pmb{x}_{k+1}=\pmb{x}_k+\Delta\pmb{x}_k
のように反復的に最適化することを考える。
この$f(\pmb{x})$について、更新前の点$\pmb{x}_k$に近い場所の点$\pmb{x}$での$f(\pmb{x})$の値は、多変数関数に対するテイラー展開より、微小なベクトル$\Delta\pmb{x}=\pmb{x}-\pmb{x}_k$を用いて、
f(\pmb{x})\approx f(\pmb{x}_k)+\nabla f(\pmb{x}_k)^T\Delta\pmb{x}+\frac{1}{2}\Delta\pmb{x}^T\nabla^2 f(\pmb{x}_k)\Delta\pmb{x}
のように表すことができる。$\pmb{x}_k$を固定した時、この右辺を最小化したい場合、
\frac{1}{2}\Delta\pmb{x}^T\nabla^2 f(\pmb{x}_k)\Delta\pmb{x}+\nabla f(\pmb{x}_k)^T\Delta\pmb{x}\tag{5}
を最小化すればいい。この式は多変数関数の2次関数で、もしこれが下に凸である場合、前節の放物線の最小化と同じように最小化できる。つまりこの式(5)を式(3)と見比べて、式(4)と同じ形の式を作ればいい。よって
\nabla^2 f(\pmb{x}_k)\Delta\pmb{x}=-\nabla f(\pmb{x}_k)
を満たす$\Delta\pmb{x}$で式(5)は最小となる。よって、この$\Delta\pmb{x}_k$を用いて、
\pmb{x}_{k+1}=\pmb{x}_k+\Delta\pmb{x}_k
と更新すれば、$f(\pmb{x})$を最小化する$\pmb{x}$を見つけることができる。このように上で述べた結論と同じことが、テイラー展開を用いた方法で説明することができる。
多変数関数の最小二乗法
多変数関数の最小二乗法について考える。
最小二乗法とは
最小二乗法とは、測定したデータに合いそうな関数を当てはめる手法で、モデル関数による計算値と実験での計測などで得られたデータの残差の二乗和が最小になるように当てめる。これも最適化問題である。
例えば、フックの法則によれば、ばねに加える力$x$とそのときのばねの伸び$y$は、ばね係数を$k$とすると
y=kx
となる。様々な大きさ$x_i$の力をばねに加え、そのときのばねの伸び$y_i$を測定することで、最小二乗法でこのばね係数$k$を求めることができる。
モデル関数を$f(x)$、計測で得られた各データ点を$(x_i,y_i)$とすると、
モデル関数に変数である$x_i$を入れた計算値$f(x_i)$と実際の測定値$y_i$の差(残差)は
r_i=f(x_i)-y_i
である。残差はひとまとめにして残差ベクトル、$\pmb{r}$と表す。そして、二乗誤差は
S=\frac{1}{2}\sum_i r_i^2
である。二乗誤差$S$が最小になる$f(x)$のパラメータを探せば、それが最も妥当なモデル関数だと思われる。
例えばモデル関数が$f(x)=ax+b$の場合、パラメータは$(a,b)$である。これは一次関数の最小二乗法で、$S$を最小にするパラメータは
\begin{align}
\frac{\partial S}{\partial a}=0\\
\frac{\partial S}{\partial b}=0
\end{align}
の解である。これは平均と分散を用いて
\begin{align}
\hat{a}=\frac{cov(x,y)}{\sigma^2(x)} \\
\hat{b}=\mu_y-\hat{a}\mu_x
\end{align}
と計算できる。詳しくは「高校数学の美しい物語」の最小二乗法(直線)の簡単な説明のページを参照
より一般的には最小二乗法とは、パラメータ$\pmb{\lambda}$が含まれるモデル関数$f(x)$について
S(\pmb{\lambda})=\frac{1}{2}\sum_i (f(x_i)-y_i)^2
となる$S(\pmb{\lambda})$の最小化問題である。ここで、モデル関数$f(x)$の変数は$x$だが、最小化の対象の$S(\pmb{\lambda})$の変数はパラメータ$\pmb{\lambda}$である点に注意すること。
多変数関数の最小二乗法に最急降下法とニュートン法を用いる
複数のパラメータ$\pmb{\lambda}$が含まれる多変数関数$f(x)$について、
計測で得られた各データ点を$(x_i,y_i)$について、
S=\frac{1}{2}\sum_i (f(x_i) - y_i)^2
を最小にするパラメータ$\pmb{\lambda}$を求めることを考える。もしこの関数が非線形だと、微分=0という式は簡単には解けない。そこで、最急降下法とニュートン法を組み合わせてパラメータを求めることができる。
前の節で述べた結果から、勾配$\nabla S(\pmb{\lambda})$とヘッシアン$H=\nabla^2 S(\pmb{\lambda})$を用いて、
H\Delta\pmb{\lambda}_k=-\nabla S(\pmb{\lambda})
を満たす$\Delta\pmb{\lambda_k}$を計算し、そして、
\pmb{\lambda}_{k+1}=\pmb{\lambda}_k+\Delta\pmb{\lambda}_k
を計算し、これを反復すれば$S(\pmb{\lambda})$を最小にするパラメータ$\pmb{\lambda}$を求められる。つまりモデル式$f(x)$の最適なパラメータ$\pmb{\lambda}$が求めることができる。
ガウス・ニュートン法
ただ、ヘッシアンは2回微分が必要で計算コスト高く、またその式を導出するのも手間がかかる。
ヘッシアンを近似することで計算量と手間を減らすのがガウス・ニュートン法である。
まず、勾配$\nabla S$を考えてみると、
\nabla S=\frac{\partial S}{\partial \pmb{\lambda}}=\left( \sum_i (f(x_i)-y_i)\frac{\partial f(x_i)}{\partial \lambda_1},\sum_i (f(x_i)-y_i)\frac{\partial f(x_i)}{\partial \lambda_2}, ...\right)^T
で、成分表示をし、さらに残差$r$を用いれば、次のように表せる。
\begin{align}
(\nabla S)_j&=\sum_i (f(x_i)-y_i)\frac{\partial f(x_i)}{\partial \lambda_j}\\
&=\sum_i r_i\frac{\partial f(x_i)}{\partial \lambda_j}\tag{6}
\end{align}
ここでヤコビアン$J$を導入する。ヤコビアンも行列でその成分$J_{ij}$は、
J_{ij}=\frac{\partial f(x_i)}{\partial \lambda_j}
である。ヤコビアンは縦が測定数、横がパラメータ数の行列となる。
よって式(6)はヤコビアンを用いて
(\nabla S)_j=
\frac{\partial S}{\partial \lambda_j}=\sum_i r_i J_{ij}
つまり、
\nabla S=J^T\pmb{r}
と表せる。
次にヘッシアン$H=\nabla^2 S$は
\begin{align}
H_{jk}&=(\nabla^2 S)_{jk}\\
&=\sum_i \left(\frac{\partial f_i}{\partial \lambda_k} \frac{\partial f_i}{\partial \lambda_j}+ (f_i-y_i)\frac{\partial^2 f_i}{\partial \lambda_j\lambda_k}\right)\\
&=\sum_i \left( J_{ik}J_{ij}+r_i\frac{\partial^2 f_i}{\partial \lambda_j\lambda_k}\right)
\end{align}\tag{7}
となる。
しかし式(7)の最後の式の右辺第2項目の2回微分は計算コストが高く、プログラムで式を実装するのも手間がかかる。ガウス・ニュートン法ではこの2回微分を無視し、ヘッシアンを
H_{jk}\approx\sum_i J_{ik}J_{ij}
つまり
H\approx J^TJ
と近似する。
以上からガウス・ニュートン法では
J^TJ\Delta\pmb{\lambda}_k=-J^T\pmb{r}
を満たす$\Delta\pmb{\lambda_k}$を計算し、そして、
\pmb{\lambda}_{k+1}=\pmb{\lambda}_k+\Delta\pmb{\lambda}_k
を計算する。これを反復することで、$S(\pmb{\lambda})$を最小にするパラメータ$\pmb{\lambda}$を求められる。つまりモデル式$f(x)$の最適なパラメータ$\pmb{\lambda}$が求めることができる。
ガウス・ニュートン法によるモデルのパラメータ推定
ガウス・ニュートン法について具体的な実装と図示を見ながら確認する。
ガウス・ニュートン法 - Wikipediaに記載されているミカエリス・メンテン式の例を借りる。詳しい内容はリンク先を参照。
(出典:[ガウス・ニュートン法」『フリー百科事典 ウィキペディア日本語版』。2020年10月29日 (木) 10:09 UTC、URL: https://ja.wikipedia.org)
酵素の基質濃度と反応速度の関係のデータがある。
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| [S] | 0.038 | 0.194 | 0.425 | 0.626 | 1.253 | 2.500 | 3.740 |
| v | 0.050 | 0.127 | 0.094 | 0.2122 | 0.2729 | 0.2665 | 0.3317 |
これに対し、ミカエリス・メンテン式をモデル関数としてフィッティングする。
v=\frac{V_{max}}{K_M+[S]}
つまり二乗誤差
S=\frac{1}{2}\sum_i (v([S]_i) - v_i)^2
を最小化するようなミカエリス・メンテン式のパラメータ$V_{max}$と$K_M$を求める。
初期値
(V_{max},K_M)=(0.2,0.8)
から出発し、収束させる。収束の推移を等高線図とプロットと矢印で描写する。

収束はしているが、等高線と垂直に降下していない、とくに最初の降下で顕著である。これはヘッシアンに近似を用いているためと考えられる。
また、二乗誤差の収束の様子を図示する。
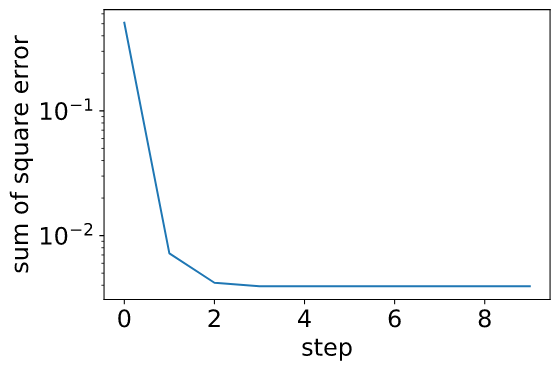
急速に、誤差関数が収束していることが分かる。
また、測定点と算出したV_maxとK_Mでミカエリス・メンテンのモデル式を図示する。

パラメータフィッティングと図を算出するため作ったPythonコードをこのページの最後の捕捉に示す。
ライブラリの利用
実際にガウス・ニュートン法を用いて多変数モデル式のパラメータを決定したい場合、自分で実装するより、上のことを分かった上で、ライブラリを使う方がいい。
scipy.optimize.least_squares
Scipyのoptimeze.least_squaresではガウス・ニュートン法よりより効果的な手法が使え、さらに制約条件についても考慮してくれるなど、機能が充実している。

この関数には手法(method)とヤコビアン(jac)を指定することができ、いくつかの手法を使う場合は、ヤコビアンを算出する関数を代入することで高速に探索ができる。もしヤコビアンを指定しない場合は、この関数内部で自動的に有限差分法でヤコビアンを算出する。自動的にヤコビアンを計算してくれるので便利に思えるが、有限差分でヤコビアンを計算すると、パラメータの数に比例して計算時間が増えてしまう欠点がある。
ここで有限差分法でのヤコビアンの計算方法について説明する。
パラメータ$\pmb{\lambda}=(\lambda_1,\lambda_2,\cdots)$でのモデル関数の計算値を$f(x)(\lambda_1,\lambda_2,\cdots)$、微小な$\lambda$の変化を$\Delta\lambda$とする。そうすると、有限差分でヤコビアンを計算する場合、最初のパラメータ$\lambda_1$に対する偏微分は
\begin{align}
J_{i1}&=\frac{\partial f(x_i)}{\partial \lambda_1}\\
&\approx\frac{f(x_i)(\lambda_1+\Delta\lambda,\lambda_2,\cdots)-f(x_i)(\lambda_1-\Delta\lambda,\lambda_2,\cdots)}{2\Delta\lambda}\\
\end{align}
と計算できる。これを各パラメータ$(\lambda_1,\lambda_2,\cdots)$について行わなければならない。よって有限差分法でヤコビアンを計算すると、計算時間はパラメータの数に比例して増えていく。
もし、$\frac{\partial f(x_i)}{\partial \lambda_j}$が解析的に計算できるのであれば、その解析式をヤコビアンの関数としてプログラムで実装し、このoptimeze.least_squaresに引数として代入すれば高速化できることになる。そしてその高速化の効果はパラメータが増えれば増えるほど大きくなることになる。
さらにこの関数の詳しい利用方法はドキュメントなどを参照。
補足
ミカエリス・メンテン式のパラメータフィッティングと図示のコード。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from matplotlib import ticker,cm
def michaelis(conce,V_max,K_m):
"""
ミカエリス・メンテン式。反応率を算出する。
"""
return V_max*conce/(K_m+conce)
def compute_j(matrix_con,p_x=np.array([[0.5],[0.5]])):
"""
モデル関数について微分し、ヤコビアンを計算する。
Args:
matrix_con : 基質濃度の1次元配列
"""
# 要素が0の縦2、横1の行列を用意
dx_base=np.zeros([2,1])
# 微小距離を定義
dx=1e-3
# ヤコビアンのリストを設定
jacobian=[]
# パラメータの数分ループ
for i in range(2):
dx_array=dx_base.copy()
dx_array[i,0]=dx
# p_xから微小距離だけ移動したベクトルを作る。
p_x_d=p_x+dx_array
# ミカエリス・メンテン式で反応率を計算する。
v_p=michaelis(matrix_con,p_x_d[0,0],p_x_d[1,0])
p_x_d=p_x-dx_array
v_m=michaelis(matrix_con,p_x_d[0,0],p_x_d[1,0])
jacobian.append((v_p-v_m)/dx/2)
return np.array(jacobian).T
# 測定データを用意
matrix_con=np.array([0.038,0.194,0.425,0.626,1.253,2.500,3.740])
cons_rate=np.array([0.050,0.127,0.094,0.2122,0.2729,0.2665,0.3317])
# 初期値を与える。
p_x=np.array([[0.8],[0.2]])
# 最小値に向かう様子の推移を記録するリストの用意
p_x_tr=[p_x.copy()]
s_tr=[]
for i in range(10):
# ヤコビアンの算出
jacobian=compute_j(matrix_con,p_x)
# 残差の算出
res=michaelis(matrix_con,p_x[0],p_x[1]) - cons_rate
# この後の行列積のため、縦測定数、横1の行列に変換
res=res[:,np.newaxis]
# 疑似ヘッシアンを算出
hessian = jacobian.T @ jacobian
# 最小値に向かう移動ベクトルを算出
d_p_x= - np.linalg.pinv(hessian) @ (jacobian.T @ res)
# 移動
p_x = p_x+d_p_x
p_x_tr.append(p_x.copy())
s_tr.append(np.sum(res**2)/2)
# 図示の準備
array_1=np.arange(0,1.2,0.01)
array_2=np.arange(0,1.2,0.01)
mat_1,mat_2=np.meshgrid(array_1,array_2)
length=matrix_con.shape[0]
sse=np.zeros_like(mat_1)
for i in range(length):
calc_cons=michaelis(matrix_con[i],mat_1,mat_2)
a_res=cons_rate[i]-calc_cons
sse += a_res**2
# 図示
plt.rcParams["font.size"] = 18
fig = plt.figure()
ax1 = fig.add_subplot(111)
lev_exp = np.arange(np.floor(np.log10(sse.min())-1),
np.ceil(np.log10(sse.max())+1))
levs = np.power(10, lev_exp)
# 等高線図を図示する。カラーマップは対数スケールとする。
cs=ax1.contourf(mat_1,mat_2,sse,levs, location=ticker.LogLocator(),norm=LogNorm())
c_bar=fig.colorbar(cs)
# 収束の推移をプロットと矢印で描写する。
for i in range(9):
ax1.plot(p_x_tr[i][0],p_x_tr[i][1],'om')
ax1.annotate('',xy=p_x_tr[i+1],xytext=p_x_tr[i],
arrowprops=dict(shrink=0,
width=1,
headwidth=8,
headlength=10,
connectionstyle='arc3',
facecolor='k',
edgecolor='k'))
ax1.plot(p_x_tr[10][0],p_x_tr[10][1],'om')
ax1.set_xlabel('V_max')
ax1.set_ylabel('K_M')
c_bar.set_label('reaction rate')
plt.show()
# 二乗誤差の収束の様子を図示
fig=plt.figure()
ax2=fig.add_subplot(111)
ax2.plot(s_tr)
ax2.set_yscale('log')
ax2.set_xlabel('step')
ax2.set_ylabel('sum of square error')
plt.show()
# 測定点と
# 算出したV_maxとK_Mでミカエリス・メンテンのモデル式を図示
conce_array=np.arange(0,4,0.1)
rr_array=michaelis(conce_array,p_x[0,0],p_x[1,0])
fig=plt.figure()
ax3=fig.add_subplot(111)
ax3.plot(conce_array,rr_array)
ax3.plot(matrix_con,cons_rate,'o')
ax3.set_xlabel('matrix concentration')
ax3.set_ylabel('reaction rate')
plt.show()