初めに
「球面集中現象」という言葉を知った.
少しだけ勉強してみる.
文献(備忘録として):
球面集中現象
2次元空間
まず,2次元空間での単位円を考える(直径$d=1$,半径$r=d/2$).
単位円の面積$S$は,
\begin{align}
S
&= \pi r^2 \\
\end{align}
である.中心から$r_* = 0.9r$以上離れた部分を,円の「表面付近」と呼ぶこととすると,その面積$S_*$は,
\begin{align}
S_{*}
&= \pi \left( r^2 - r_{*}^2 \right) \\
&= \pi \left( r^2 - (0.9r)^2 \right) \\
&= 0.19 \pi r^2 \\
\end{align}
である.円全体の内,19%が「表面付近」である.
3次元空間
続いて,3次元空間での単位球を考える.
単位球の体積$V$は,
\begin{align}
V
&= \frac{4}{3} \pi r^3 \\
\end{align}
である.先ほどと同様に,中心から$r_* = 0.9r$以上離れた部分を,球の「表面付近」と呼ぶこととすると,その体積$V_*$は,
\begin{align}
V_{*}
&= \frac{4}{3} \pi \left( r^3 - r_*^3 \right) \\
&= \frac{4}{3} \pi \left( r^3 - (0.9r)^3 \right) \\
&= 0.271 \frac{4}{3} \pi r^3 \\
\end{align}
である.球全体の内,27%が「表面付近」である.
d次元空間
より一般化して,$d$次元空間を考える.
ここで,$d$次元空間において,相似な図形の体積比が相似比の$d$乗に比例する性質を利用する.
すなわち,$d$次元超球の体積$V(d)$と,その「表面付近」の体積$V_*(d)$との比は
V(d) : V_*(d) = 1 : 1 - R^d
となる.ただし,$R$は相似比である.
実際,
- $d=2$では,$V(d) : V_*(d) = 1 : 1 - 0.9^2 = 1 : 0.19$
- $d=3$では,$V(d) : V_*(d) = 1 : 1 - 0.9^3 = 1 : 0.27$
より,先ほどの計算結果と一致する.
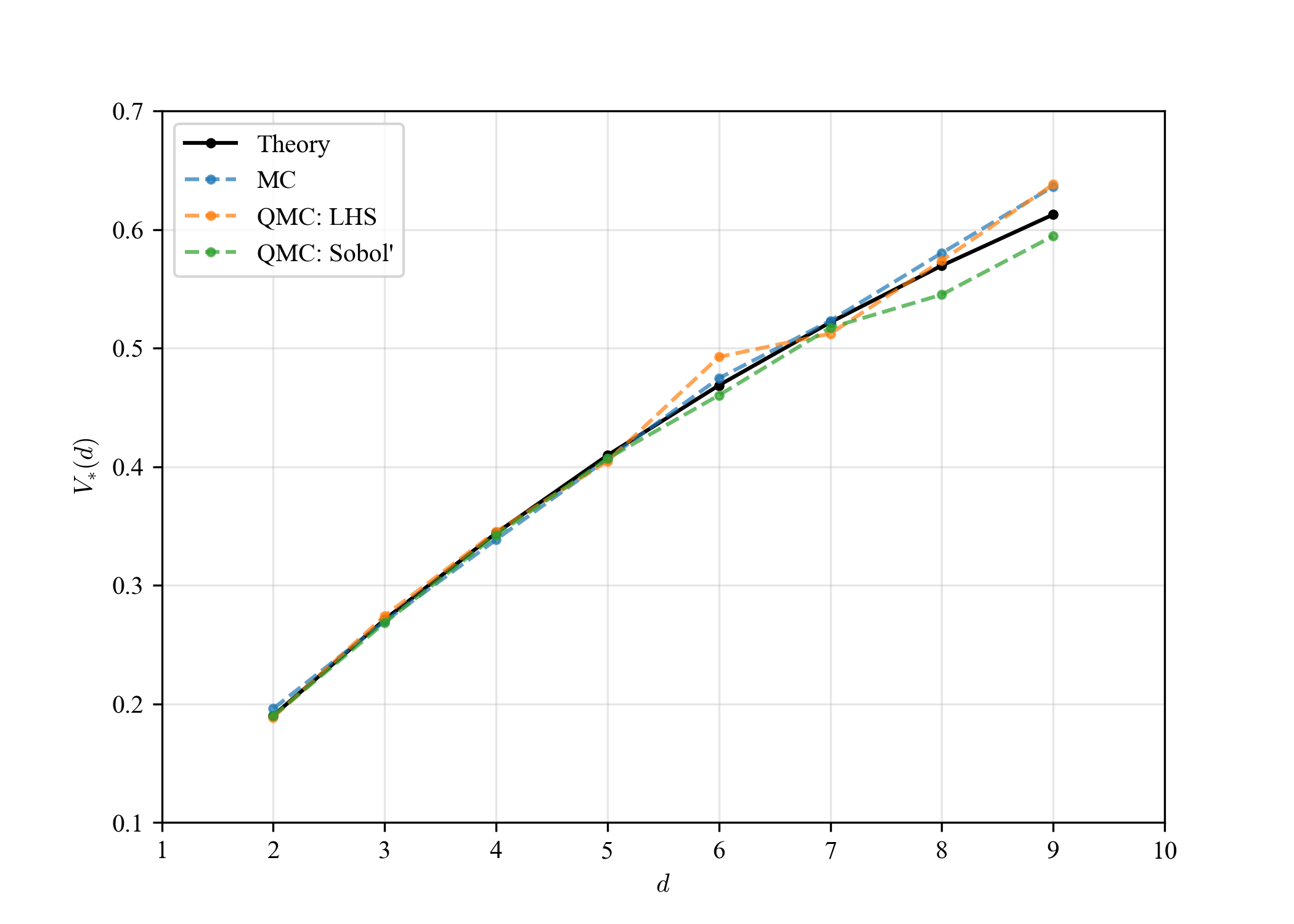
空間次元$d$を大きくしながら$V_*(d)$を計算すると,以下のようになる.
高次元になるほど,「表面付近」の割合が大きくなる.
幾つかのサンプリングを試したが,MCだけでなく,QMCでも起きるようである.
記憶が曖昧だが,何処かでLHSは球面集中現象を回避,或いは緩和できると聞いた気がするが,実験の結果,MCとLHSはそう変わらない気がする.或いは,コードにバグがあるかもしれないが.
終わりに
最近は,分からないことだらけである.
Appendix
import numpy as np
from scipy.stats import qmc
import matplotlib.pyplot as plt
m = 32 # repeat
n = 2**10 # sample size
ds = np.arange(2, 10, 1) # dimensions
V_star_list = []
for d in ds:
res_list = []
for i in range(m):
X = np.random.uniform(size=(n, d))
# X = qmc.LatinHypercube(d=d).random(n=n)
# X = qmc.Sobol(d=d).random(n=n)
rs = 0.
for j in range(len(X.T)):
rs += X[:,j]**2
rs = np.sqrt(rs)
count = 0
count_in = 0
for r in rs:
if r < 1.:
count += 1
if r < .9:
count_in += 1
res = count_in / count
res_list.append(res)
print(f"d:{d:d}, V_star: {1. - np.mean(res_list):.2f}")
V_star_list.append(1. - np.mean(res_list))