初めに
以前から気になっていた(Jiao+2024).
Methods
境界だけ$L^2$の代わりに$H^1$を使うと良いらしい.これをSPINN(Stabilized PINN)と呼ぶ.
Results
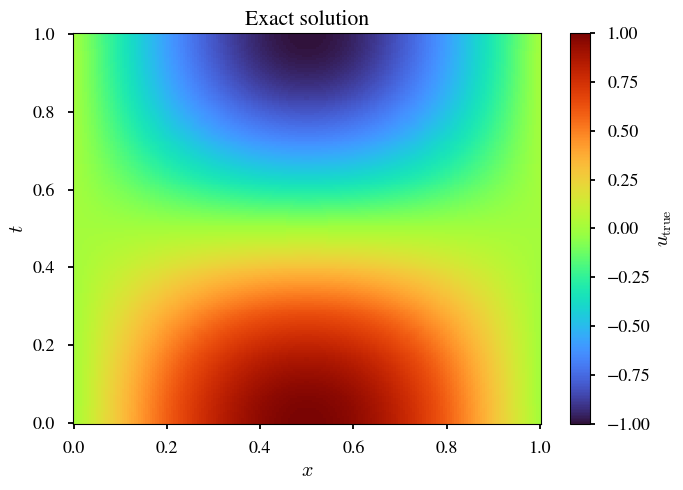
簡単な波動を与える.
乱数シードを完全に支配し,全く対照な実験を設定した.
倍精度を採用した.
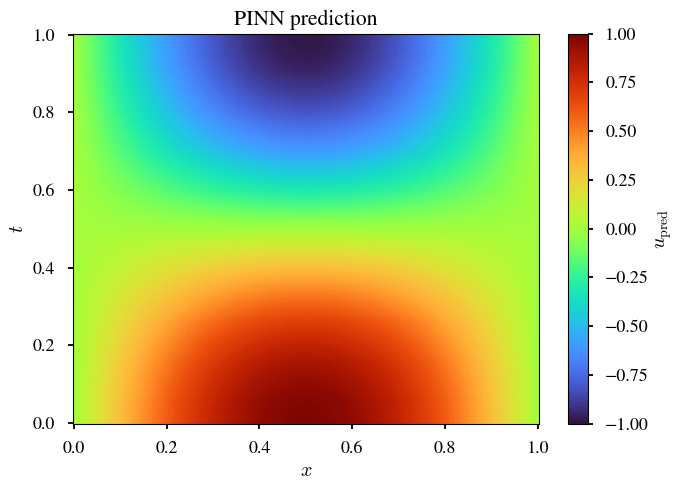
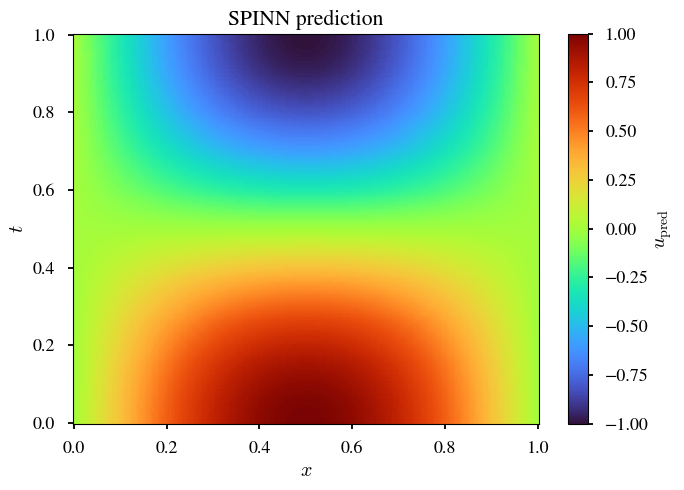
| Exact | PINN | SPINN |
|---|---|---|
 |
 |
 |
 |
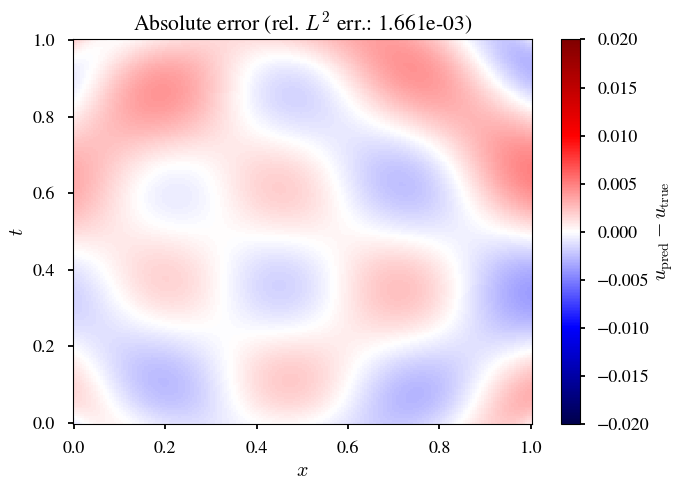 |
|
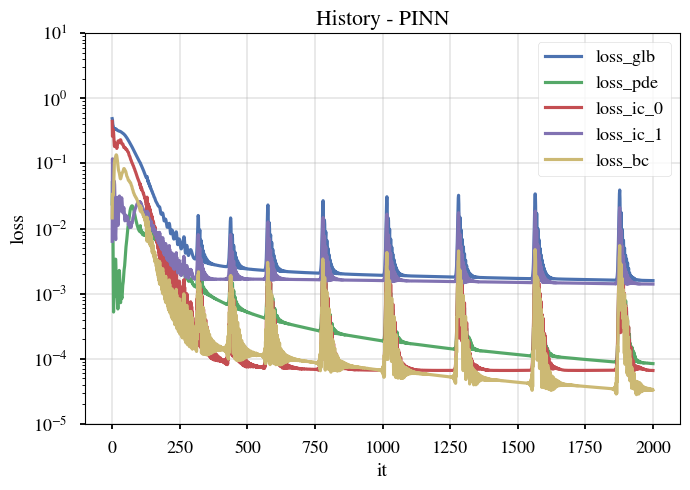 |
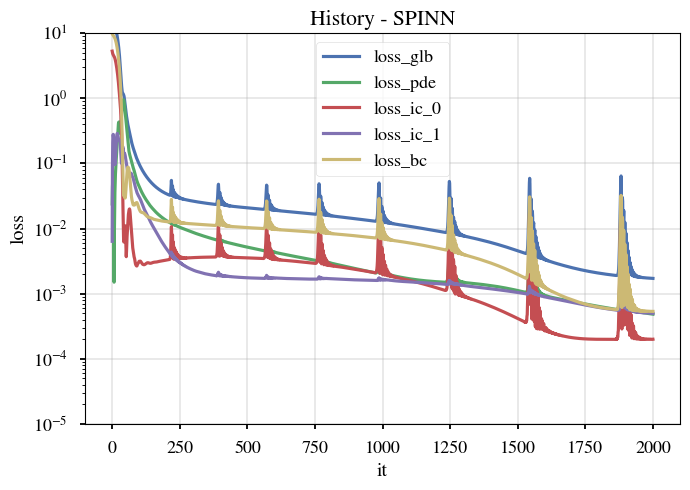 |
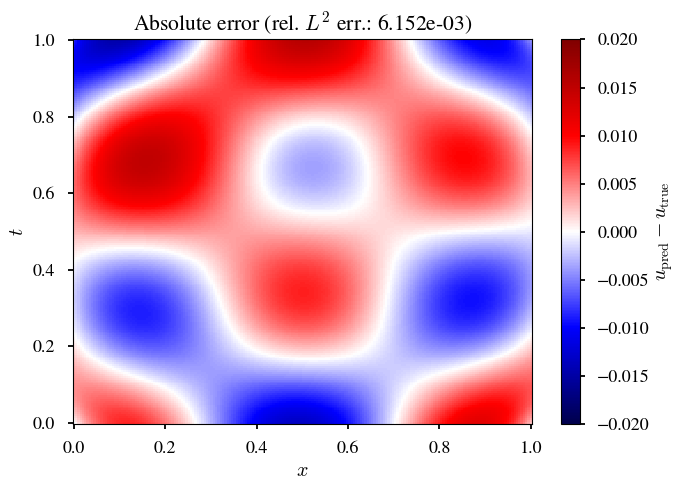
境界周りで,より,平滑化が効く.
終わりに
後から思い出したが,gPINN(Yu+2022)と似ている.gPINNは逆に,領域内が$H^1$か.
2025年11月10日,gIB-PINN(Wang+2025)を見つけた.これは,境界条件だけ見るとSPINNと同じだが,初期条件の時間微分を押さえつけているようなので,時間発展する系に適用するときに違いが現れる.定常問題では SPINN = gIB-PINN に見える.また,gIB-PINNは,領域内を$H^1$で押さえることをしない.
Sobolev trainingの変種が増えてきた気がする.