始めに
活性化関数で有名なものとして,ReLU[1]があります.ReLUが有名になった(かつ,ReLUがディープラーニングを有名にした)のは,2012年頃でしょうか.数年前,ReLUと同様にブレイクスルーを起こした関数は,Swish[2](あるいはSiLU[3])でした.その後,幾つか新しい関数も提案されていますが[4, 5],取り立てて尖った研究成果は未だ発見されいない感覚です.
Swishは,感覚的には「ズームアウトするとReLUじゃん?」って感じですよね.事実,論文[2]も幾つかの条件の下ではReLUに(あるいは線形写像に)漸近することを述べてくれています.もう少し広い枠組みで考えると,SwishはReLUの一般化として解釈できそうな気がします!本稿は,この仮説が合っているかを簡単に検証するものです(コードはこちらに公開しています).
Swishの極限(タイトルほんま?)
まず,Swishの定義を確認しておくと,
\begin{align}
\tau(x; \beta) &= x \cdot \sigma(\beta x) \\
&= \frac{x}{1+\exp(- \beta x)}
\end{align}
ここで,$ \tau(\cdot) $はSwish関数,$ \sigma(\cdot) $はSigmoid関数,$ \beta $は固定値あるいは学習可能パラメータです.また,$x$は,この非線形写像を備えた隠れ層に飛び込んでくる特徴量です.Swishは線形関数とReLUの合いの子であり[2],$ \beta $を調整することで(あるいは,極限操作の下で)線形関数に近づけたりReLUに近づけたりできます.
実際に計算してみると,$\beta \rightarrow 0$では,
\lim_{\beta \to 0} \frac{x}{1+\exp(- \beta x)} = \frac{x}{2}
(右極限と左極限は一致)であり,一方,$\beta \rightarrow \infty$では,
\lim_{\beta \to \infty} \frac{x}{1+\exp(- \beta x)} = \text{ReLU}(x)
です.少し丁寧にいけば,$\sigma(\beta x) \xrightarrow{\beta \rightarrow \infty} H(x)$ですので,これに$x$をかければReLUになりますね($H(\cdot)$はヘヴィサイトのステップ関数).
やはり,Swishは $\beta$ をうまいこと調整すれば線形になったりReLUになったりしそうです(ほぼ論文[2]の通りですが,自分なりに解釈できた).論文[2]の主張を尊重すれば $\beta$ は学習パラメータとすべきなのでしょうが,本稿ではハイパーパラメータとして取り扱います.因みに,GELU ($\approx \tau(x; \beta=1.702)$) [6]も幾つか良い成績を残しており[7],ReLUのように,正則化機能と滑らかさを兼ね備え,かつ勾配が大きく取れる関数が良さげなトレンドですね[2, 3, 4]!
最後に,1/2倍にスケーリングされた線形写像とReLU,そして $\beta$ をいじったSwishを図示しておきます.グレーの実線で線形写像 / ReLUを示しており,色付きの破線が $\beta$ を逐次変更したSwish,赤い破線が極限となっています.下図からもやはり,$\beta$ を少しずつ変えると様子が変わり,線形写像に近づいたりReLUに近づいたりしています.
| Linear vs. Swish | ReLU vs. Swish |
|---|---|
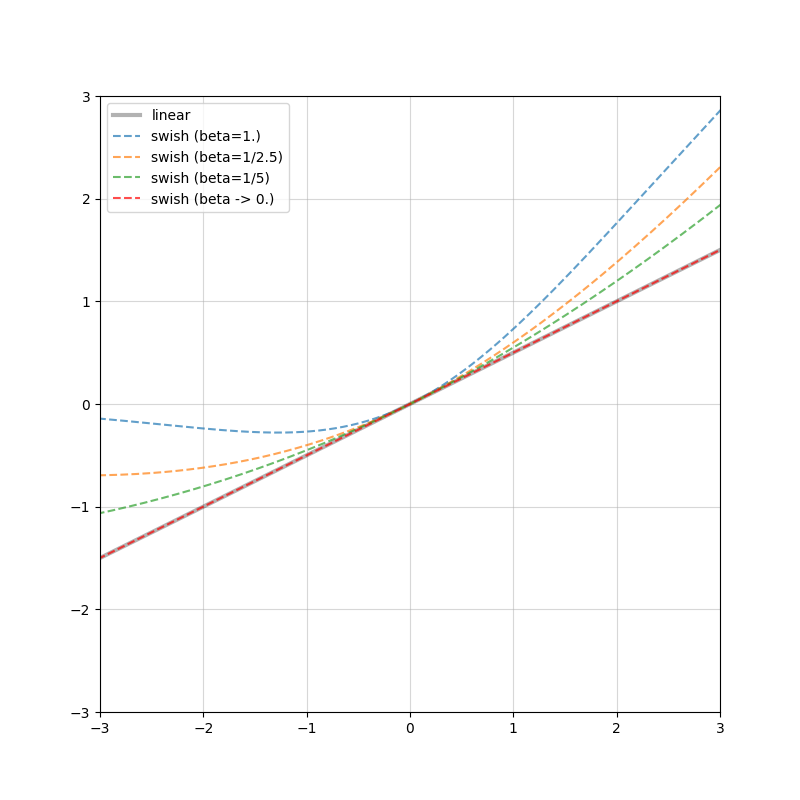 |
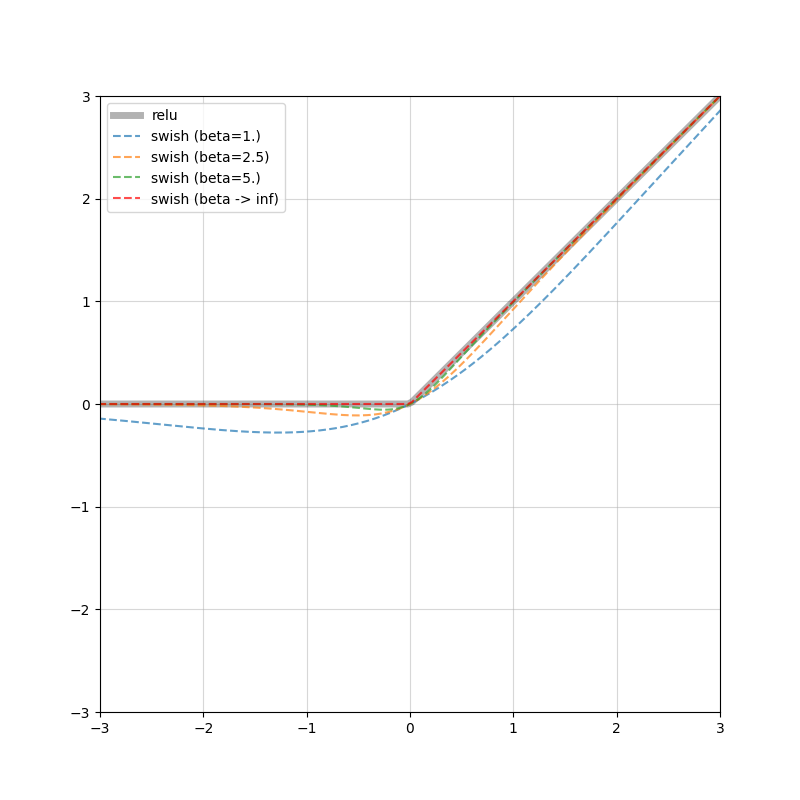 |
数値実験
以前の投稿で用いたものと同一の数値実験を取り上げます.Swishに与える$\beta$(本稿ではスケーリングファクターと呼ぶこととします)には,$\beta=1/5, 1/2.5, 1.0, 2.5, 5.0$ の5パターンを採用します.また,用いるDNN構造は全て同一のものとしており,Width=5, Depth=3の全結合ニューラルネットワークを採用,学習率5e-4のAdamによるフルバッチ学習を30,000エポックだけ実行します.early stopping patienceは100エポックとしています.また,重みの初期化は,ReLU型の関数であることを考慮してHe normalを採用しています.
実験1(Linear vs. Swish)
ここではまず,Swishが線形関数に近づくことを確認します.ここでは,$\beta=1.0, 1/2.5, 1/5$ のSwish ($\tau(x; \beta) = x \cdot \sigma(\beta x)$) と,スケーリングされた線形写像 ($f(x) = \frac{x}{2}$) の4パターンを比較します.
学習する関数は,以下のものです:
f(x) = 0.7 \sin(\pi x) + 0.3\sin(4 \pi x), x \in [-1, 1]
では早速,近似曲線を確認しましょう!
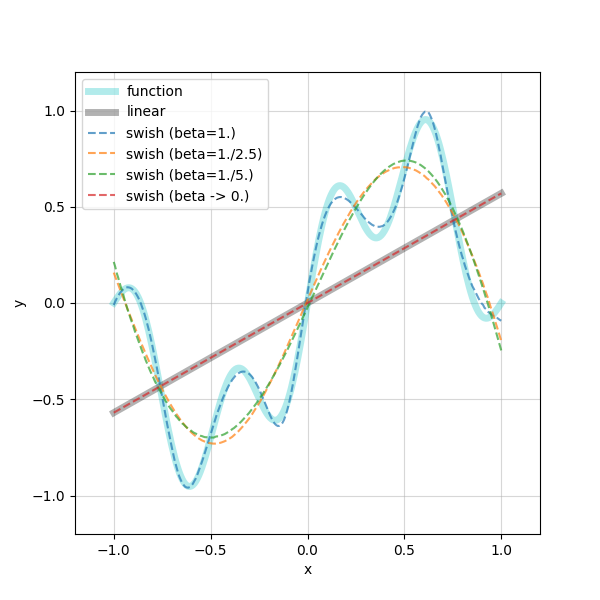
真の関数(シアンの実線)に対して,$\beta=1.0$ のSwishは,良い近似を与えていますが,$\beta=1/2.5, 1/5$ ではかなり外れています.また,$\beta \rightarrow 0$ の近似(赤色の破線)は線形写像を活性化関数としたDNN(グレーの実線)にほぼ一致しています.また,以下には損失関数の推移を示します.
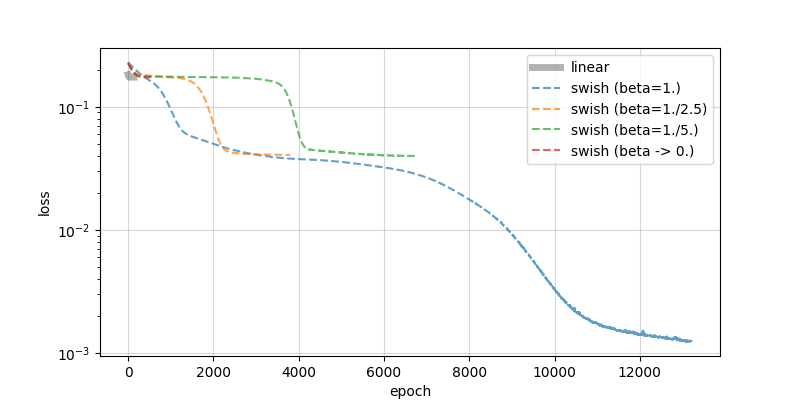
近似曲線の状況と損失関数の収束過程からも,Swishが少しずつ線形写像に近づいています.実験を通して,極限操作の下で $\tau(x; \beta) \rightarrow \frac{x}{2}$ であることが確認できました.
実験2(ReLU vs. Swish)
続いて,SwishがReLUに近づくことを確認しましょう.比較する活性化関数は,$\beta=1.0, 2.5, 5.0$ のSwish ($\tau(x; \beta) = x \cdot \sigma(\beta x)$) とReLU ($f(x)=\max(0, x)$) の4パターンです.
g(x) = \exp(x) \sin(2 \pi x), x \in [-1, 1]
続いて,近似を確認します.

今回は,真のシグナル(シアンの実線)に対して,実験した全てのSwishが良いフィッティングを与えているように見えます.ただ,極限操作を掛けたSwishとReLUがほぼ重なる傾向は先ほどと同様です.さらに,損失関数の推移を以下に示します.
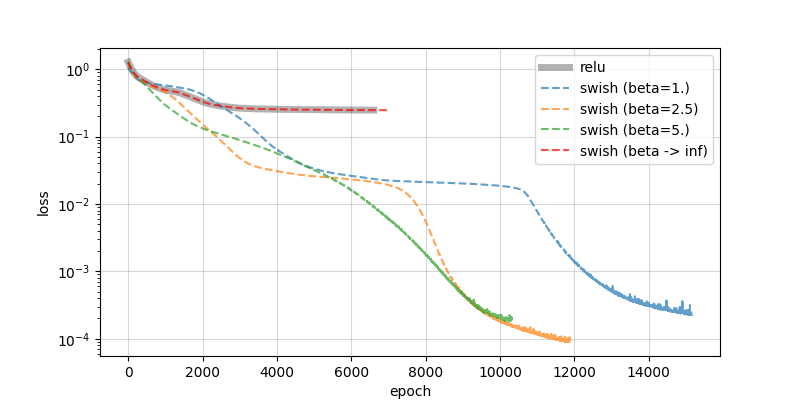
実験1とほぼ同様に,損失関数の収束の様子はReLUと極限をとったSwishでほとんど同一の動きをしています.その他の $\beta$ をとったSwishたちは,皆良く収束している印象です.本来であれば,スケーリングファクター $\beta$ によって勾配も定数倍されそうなので学習率を調整しないと等価な比較と言えないかもしれませんが,少なくとも本稿のスコープは達成できたと言ってで良いでしょう.
終わりに
出来レースではありましたが,論文[2]の主張を受け,極限操作と数値実験を通して仮説の検証を行いました.
ただ,少しだけ $\beta$ をいじるくらいでは関数の挙動が大きく変わることはなく(事実,early stoppingをしなければどの問題でも良く近似できます),大袈裟なスケーリングをするとやっと変化が明確になるという印象でした.一方,問題によっては少し変えるだけでも良い結果になる可能性もありますので(GELU[6]はその最たる例ですね),様々な形で試すと面白そうです.
参考文献
[1] Nair, V., Hinton, G.E.: Rectified Linear Units Improve Restricted Boltzmann Machines, International Conference on Machine Learning (ICML), pp. 807–814, 2010. [paper]
[2] Ramachandran, P., Zoph, B., Le, Q.V.: Swish: a Self-Gated Activation Function, arXiv: 1710.05941, 2017. (paper)
[3] Elfwing, S., Uchibe, E., Doya, K.: Sigmoid-weighted linear units for neural network function approximation in reinforcement learning, Vol. 107, pp. 3-11, Neural Networks, 2018. (paper)
[4] Misra, D.: Mish: A Self Regularized Non-Monotonic Activation Function, arXiv: 1908.08681, 2019. (paper)
[5] Noel, Mathew Mithra and L, Arunkumar and Trivedi, Advait and Dutta, Praneet: Growing Cosine Unit: A Novel Oscillatory Activation Function That Can Speedup Training and Reduce Parameters in Convolutional Neural Networks, arXiv: 2108.12943, 2021. (paper)
[6] Hendrycks, D., Gimpel, K.: Gaussian Error Linear Units (GELUs), arXiv: 1606.08415, 2016. (paper)
[7] Devlin, J., Chang, M.W., Lee, K., Toutanova, K.: BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding, arXiv: 1810.04805, 2018. (paper)
[8] He, K., Zhang, X., Ren, S., Sun, J.: Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, International Conference on Computer Vision (ICCV), pp. 1026-1034, 2015. (paper)
[9] 以前の記事: DNNフィッティングと活性化関数の選択