始めに
深層ニューラルネットワーク(DNN: Deep Neural Network / ANN: Artificial Neural Network / MLP: Multi-Layer Perceptron)による関数近似において,活性化関数は慎重に選択しなければならないことが知られています.僕もそのこと自体は知識として理解していながら,実際に自分の手でテストしたことが無かったので調査してみようと思いました.本投稿では,関数近似の問題を取り上げ,活性化関数の選択が近似曲線に与える影響を調べてみます.なお,ニューラルネットワークに関する基本的な議論は省きます.
また,Deep LearningのフレームワークにはTensorFlowとPyTorchがあります(もちろん,JAXやChainerなどの存在も認知しています)が,勉強のため両者のコード実装を行います.コードはGitHubに公開しているので,興味がある方はどうぞ.
(2022/04/29現在,torchコードは勉強中&開発中です.実装までもう少々お待ちください.)
活性化関数(+ DNNの設計 / 学習の設定)
テストする活性化関数は,
くらいにしようと思います.その他のGeLUやMish,GCUなど,新しい関数たちのことも知っているつもりですが,ここではある程度実績のある関数たちのみに着目します(特に,僕が気になっていることはこの子たちでカバーできるはず).
ニューラルネットワークに関する説明は省きます.Depth=3,Width=5の全結合層を積み重ね,Adamによるフルバッチ学習を行います.tanhでの重み初期値はGlorot Normal,ReLU,SwishではHe Normalを採用しました.また,近似する関数は256点で評価していますが,DNNに与える学習データは16点のみとしています.出力層の活性化関数は恒等写像,損失関数は平均二乗誤差,学習率は5e-4,エポック数は30,000です.なお,early stopping criterionは100としました.今回はtraining / validation / test datasetの分割はしていないのでこの辺りちょっと怪しいですが,許してください.
数値実験
上記の通りの問題設定で,幾つかの数値実験を行います.
実験 1
始めの例題は,以下の関数のフィッティングとします.
f(x) = 0.7 \sin(\pi x) + 0.3\sin(4 \pi x), x \in [-1, 1]
係数は適当に与えました.
早速,DNNによる近似曲線を見ましょう.
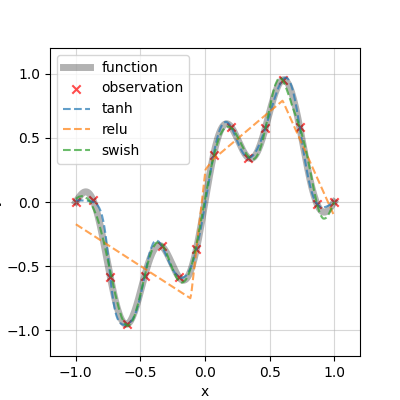
tanhとSwishによる近似は良い感じですが,ReLUによる近似だけは明らかに様子が違いますね.ほーん.続いて,損失関数の推移を確認します.

どのモデルも,初めの8,000エポックの間は学習が停滞していますが,その後急速に収束しています.どうやら学習率が大きかったようですが,許容します.それと,途中でearly stoppingがかかって30,000エポックも回っていないですが,十分でしょう.reluは収束しないまま学習が打ち切られており,長時間学習させればわんちゃん...?という気もしますが,early stoppingをかけないで50,000エポック学習させても大差の無い結果でした.
実験 2
次の例題は,三角関数に指数関数を重ねたものです.
g(x) = \exp(x) \sin(2 \pi x), x \in [-1, 1]
学習の設定は先ほどの例題と同一なので,近似を見ます.
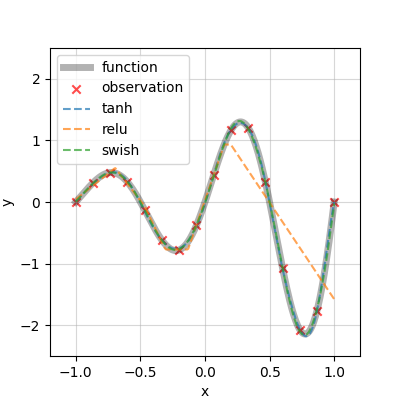
これも同じで,ReLUによる近似だけがかなり悪いです.$ x < 0 $の領域は良さげですが,$ 0 < x $では一気に外れていますね(実は$ x < 0 $でもズームすればReLUは外れています).続いて損失関数も見ましょう.

今回は大分速く収束しましたね.ReLUだけ学習が進まず打ち切られているのも同じ結果です.
さて,うまく学習できたtanh / Swishと,学習に苦戦したReLUの違いは何でしょうか?それは関数の滑らかさだと考察します.tanhおよびSwishは全域で滑らかな$ C^{\infty} $級の関数,一方,ReLUはx=0の点で特異点を持つ$ C^{0} $級の関数です.今回取り上げた2例題では関数は滑らかで,近似関数にも滑らかさが欲しいところです.ここでカクカクした形のReLU関数を使ったために,ReLU近似はカクカクしてしまったのだと考えます(TensorFlow Playgroundでも似た傾向が確認できます).
終わりに
幾つかの例題から,活性化関数が持つ非線形性が,直接DNN近似の非線形性に紐付けられることを確認しました.DNNの非線形性は活性化関数によってもたらされるものなので,これは自然なことで良く知られている性質です.ただ上記の通り,実際に自分の手で実験してみるとなるほど~!となりますね.また,物理現象を学習する際,物理量は空間的・時間的に滑らかであることが多いです.現象を特徴付ける物理量を学習・推論する際には滑らかさを備えた活性化を選択することが重要そうですね!
なお,明確化すべきは,ReLUが良いパフォーマンスを示したのは多クラス分類の分野であるということです.分類問題では出力層にソフトマックス関数をかけるので,出力層に入る直前までカクカクしていたシグナルが,出るときには滑らかになっているという寸法ですね!分類と回帰は共通している部分がとても多いですが,やはり別々のタスクです.活性化関数は慎重に選択しましょう!
参考文献
[1] Hornik, K., Stinchcombe, M., White, H.: Multilayer feedforward networks are universal approximators, Neural Networks, Vol. 2, No. 5, pp. Pages 359-366, 1989. (paper)
[2] Glorot, X., Bengio, Y.: Understanding the difficulty of training deep feedforward neural networks, Proceedings of Machine Learning Research, Vol. 9, pp. 249-256, 2010. (paper)
[3] He, K., Zhang, X., Ren, S., Sun, J.: Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, International Conference on Computer Vision (ICCV), pp. 1026-1034, 2015. (paper)
[4] Nair, V., Hinton, G.E.: Rectified Linear Units Improve Restricted Boltzmann Machines, International Conference on Machine Learning (ICML), pp. 807–814, 2010. (paper)
[5] Ramachandran, P., Zoph, B., Le, Q.V.: Swish: a Self-Gated Activation Function, arXiv: 1710.05941, 2017. (paper)
[6] Elfwing, S., Uchibe, E., Doya, K.: Sigmoid-weighted linear units for neural network function approximation in reinforcement learning, Vol. 107, pp. 3-11, Neural Networks, 2018. (paper)