More than 3 years have passed since last update.

ディープラーニング講座「深層学習：Day3」要点まとめ＆実装演習

Last updated at 2021-01-11Posted at 2020-12-31

私は、2020年7月に「G検定（2020 #2）」に合格した。
次は、2021年2月実施の「E資格（2021 #1）」受験資格である__JDLA認定プログラム「３カ月で現場で潰しが効くディープラーニング講座」__に2020年8月から挑戦中。

本記事では、__JDLA認定プログラム「3カ月で現場で潰しが効くディープラーニング講座」の課題であり、「深層学習：Day3」__実装演習結果をまとめる。

1.「深層学習：Day3」講義動画の要点まとめ

Section1）再帰型ニューラルネットワークの概念

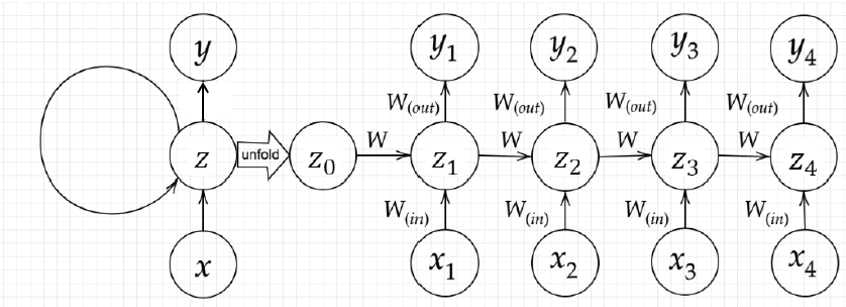
　__再帰型ニューラルネットワーク（Recurrent neural network）（以降RNNと呼ぶ）__とは、__時系列データ__を対応可能としたニューラルネットワークである。時系列データ__とは、「時間的順序を追って一定間隔ごとに観察され、しかも相互に統計的依存関係が認められるようなデータの系列」__のことで、具体的なデータ例としては、音声データ、株価データ、テキストデータ（単語のつながりに時間的順序がある）などがある。

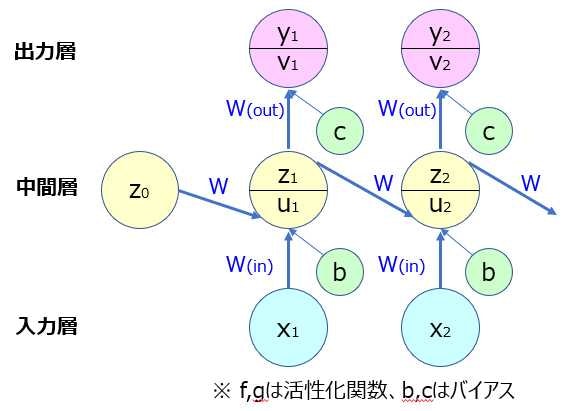
　RNNの基本構造は、他のニューラルネットワークと同様、入力層（x）、中間層（z）、__出力層（y）__からなるが、他のネットワークとの違いは、__出力層や中間層からの出力も入力として取り扱う__ことである。そして、RNNの重みは、前の中間層からの重みも加えられる。また、RNNの特徴は、__初期の状態と過去の時間$t-1$の状態を保持し、そこから次の時間での$t$を再帰的に求める再帰構造となっていること__である。

RNNの数学的記述：


\begin{align}
u^t&= W_{(in)}x^t+Wz^{t-1}+b \\
z^t&= f(W_{(in)}x^t+Wz^{t-1}+b) \\
v^t&= W_{(out)}z^t+c \\
y^t&= g(W_{(out)}z^t+c) \\
\end{align}


u[:,t+1]=np.dot(X,W_in)+np.dot(Z[:,t].reshape(1,-1),W)
z[:,t+1]=functions.sigmoid(u[:,t+1])

　RNNの逆伝播には__BPTT__という手法を活用する。BPTTとは、__RNNにおいてのパラメータ調整方法（誤差逆伝播）の一種__である。

RBPTTの数学的記述：


\begin{align}
\frac{ \partial E }{ \partial W_{in}}&=\frac{  \partial E }{ \partial u^t} \Bigl[\frac{ \partial u^t}{ \partial W_{in}} \Bigr]^T = \delta^t[x^t]^T \\
\frac{ \partial E }{ \partial W_{out}}&=\frac{  \partial E }{ \partial v^t} \Bigl[\frac{ \partial v^t}{ \partial W_{out}} \Bigr]^T = \delta^{out,t}[z^t]^T \\
\frac{ \partial E }{ \partial W}&=\frac{  \partial E }{ \partial u^t} \Bigl[\frac{ \partial u^t}{ \partial W} \Bigr]^T = \delta^t[z^{t-1}]^T \\
\frac{ \partial E }{ \partial b}&=\frac{  \partial E }{ \partial u^t} \frac{ \partial u^t}{ \partial b} = \delta^t \\
\frac{ \partial E }{ \partial c}&=\frac{  \partial E }{ \partial v^t} \frac{ \partial v^t}{ \partial c} = \delta^{out,t} \\
\end{align}

BPTTのパラメータ更新式


\begin{align}
W_{(in)}^{t+1}&=W_{(in)}^{t} - \epsilon \frac{ \partial E }{ \partial W_{(in)}} \\
&=W_{(in)}^{t} - \epsilon \sum_{z=0}^{T_t} \delta ^{t-z} [x^{t-z}]^T
 \\
W_{(out)}^{t+1}&=W_{(out)}^{t} - \epsilon \frac{ \partial E }{ \partial W_{(out)}} \\
&=W_{(out)}^{t} - \epsilon \delta^{out,t}[z^t]^T
 \\
W^{t+1}&=W^{t} - \epsilon \frac{ \partial E }{ \partial W} \\
&=W^{t} - \epsilon \sum_{z=0}^{T_t} \delta ^{t-z} [z^{t-z-1}]^T
 \\
b^{t+1}&=b^{t} - \epsilon \frac{ \partial E }{ \partial b} =b^{t} - \epsilon \sum_{z=0}^{T_t} \delta ^{t-z} \\
c^{t+1}&=c^{t} - \epsilon \frac{ \partial E }{ \partial c} =c^{t} - \epsilon \delta^{out,t} \\
\end{align}

Section2）LSTM

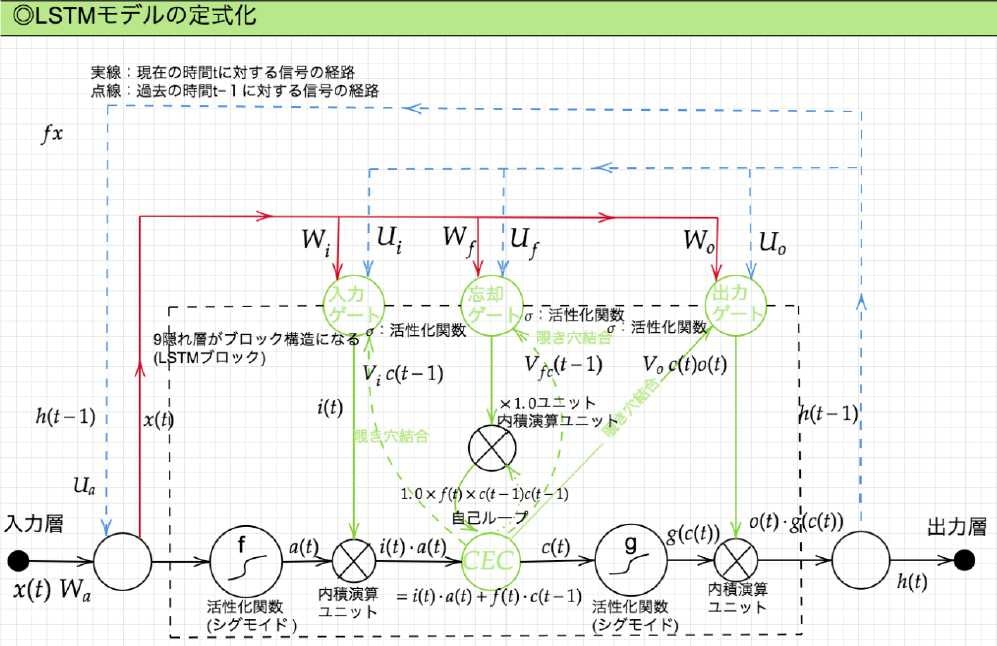
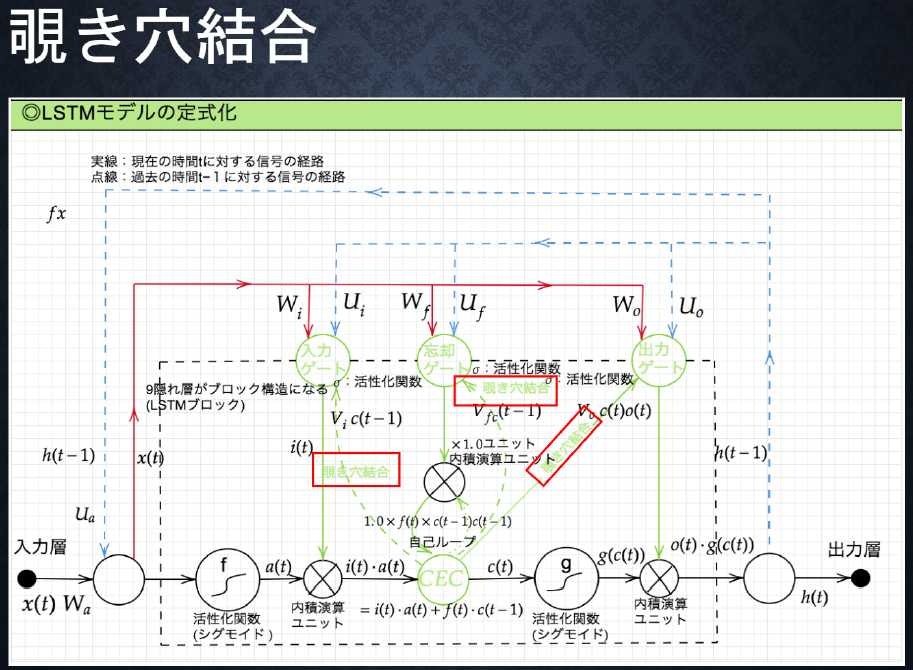
　RNNの課題は、時系列を遡れば遡るほど勾配が消失していくことであり、長い時系列の学習が困難である。そこで、構造自体を変えて勾配消失問題や勾配爆発問題（※）を解決したものが__LSTM（Long short term memory）__である。

※勾配爆発：勾配消失とは逆に勾配が層を逆伝播するごとに指数関数的に大きくなっていく問題

LSTMの全体図：
黒点線：中間層範囲
実線：現在の時間$t$に対する信号の経路
青点線：過去の時間$t-1$に対する信号の経路

LSTMで使われている関数
$a(t)$：入力から活性化関数後の情報
$i(t)$：入力ゲートからの覚えてほしい情報
$f(t)$：忘却ゲートからのどれくらい覚えておくか、どれくらい忘れるかの情報
$c(t)$：現在CECが覚えている情報


\begin{align}
c(t)=i(t)*a(t)+f(t)*c(t-1)
\end{align}

LSTMの機能：
入力ゲート：CECに覚えさせることをCECに指示する。前回の出力と今回の入力値を元に今回どうCECに記憶させるか。
出力ゲート：CECの情報をどう利用するかを決める。前回の出力と今回の入力を元に今回どれくらいの情報を利用するか。
CEC(LSTMの重要部）：__記憶機能のみを持つ。__時間依存度に関係なく、重みが一律であるため、学習機能は周囲の機能（入力ゲート、出力ゲート等）に持たせている。
忘却ゲート：前回の出力と今回の入力値を元に覚えておく情報、忘れる情報をCECに指示する。
勾配消失、勾配爆発は、勾配が1であれば発生しない。この勾配を1にするために導入されたものが__CEC__である。


\begin{align}
\delta ^{t-z-1} = \delta ^{t-z} \bigl \{ Wf^{'}(u^{t-z-1}) \bigr \} = 1 \\
\end{align}

覗き穴結合とは、CEC自身の値に、重み行列を介して伝播可能にした構造。実際はあまり効果が得られず、利用されないものとなっている。

Section3）GRU

　__GRU（Gated Recurrent Unit）__は、__LSTM__の__パラメータが多く計算負荷が高くなる問題の改良版__として開発された。パラメータは大幅に削減したものの、精度は同等以上が望めるよう構造から改善している。

GRUの全体図：
黒点線：中間層範囲
実線：現在の時間$t$に対する信号の経路
青点線：過去の時間$t-1$に対する信号の経路
GRUの機能
リセットゲート：長期記憶を忘却させるのか、それとも保持させるのかを制御
更新ゲート：長期記憶に加わる候補を計算
GRUで使われている関数
$r(t)$：リセットゲートからの出力関数
$z(t)$：古い長期記憶と現在の記憶を混合する割合を表す関数
$h(t)$：更新した長期記憶を表す関数


\begin{align}
r(t)&=W_r x(t)+U_r*h(t-1)+b_h(t) \\
z(t)&=W_z x(t)+U_z*h(t-1)+b_z(t) \\
h(t)&=z(t)*h(t-1)+(1-z(t))*h(t) \\
\end{align}

Section4）双方向RNN

　__RNN__が順伝播において過去から未来へと一方向のみだったのに対し、__双方向RNN__は、過去から未来への順伝播と、未来から過去への逆伝播を組み合わせたもの。過去の情報だけでなく、未来の情報を加味することで、精度を向上させているモデル。具体的な使用例は、__機械翻訳__や__文章の推敲__等で用いられる。

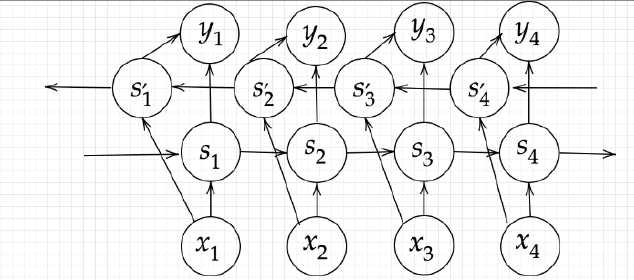
双方向RNNの構造
入力層：$x_〇$
出力層：$y_〇$
中間層（過去→未来）：$s_〇$
中間層（未来→過去）：$s_〇^{'}$

Section5）Seq2Seq

　__seq2seq__は、2つのRNNが組み合わせ実現されているモデルで、__時系列のデータを入力し、時系列のデータを出力する__モデル。一つ目のRNNで文の意味がベクトル表現に変換保持され、二つ目のRNNでベクトル表現から別の表現を出力する。一つ目のRNNのことを、__Encoder RNN__と言い、二つ目のRNNのことを、__Decoder RNN__と言う。また、seq2seqは上記より__Encoder-Decoderモデル__の一種。

seq2seqの全体図

5-1. Encoder RNN

　__Encoder RNN__とは、ユーザーがインプットしたテキストデータを単語等のトークンに区切って渡す構造。Encoder RNNで自然言語を数字に変換する。

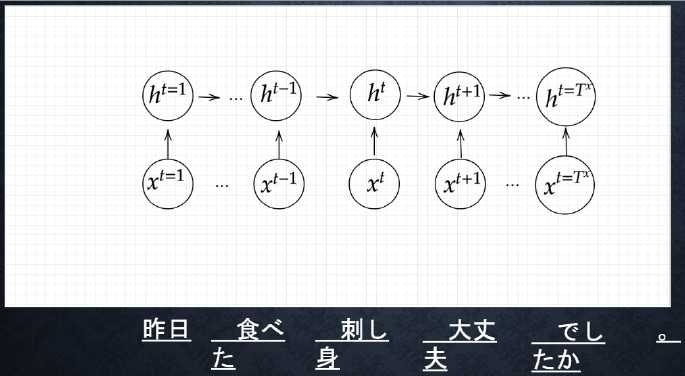
Token：文章を単語等のトークン毎に分割し、トークン毎のIDに分割
Embedding：IDから、そのトークンを表す分散表現ベクトルに変換
Encoder RNN：ベクトルを順番にRNNに入力

Encoder RNNの処理手順：
vec1をRNNに入力し、hidden stateを出力。このhidden stateと次の入力vec2をまたRNNに入力してきたhidden stateを出力するという流れを繰り返す。
最後のvecを入れたときのhidden stateをfinal stateとしてとっておく。このfinal stateがthought vectorと呼ばれ、入力した文の意味を表すベクトルとなる。

5-2. Decoder RNN

　__Decoder RNN__とは、システムがアウトプットデータを単語等のトークン毎に生成する構造。

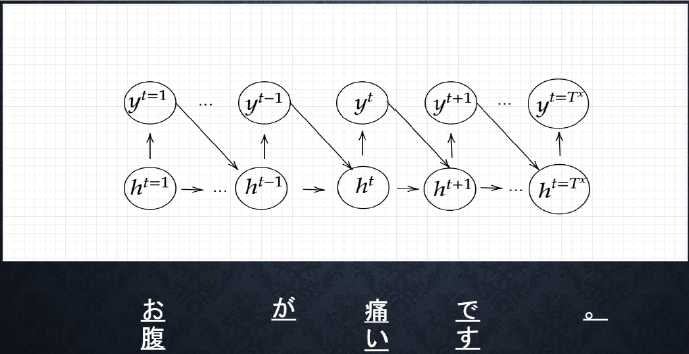
Decoder RNNの処理手順：

Decoder RNN：Encoder RNNのfinal state(thought vector)から、各トークンの生成確率を出力していく。Encoder RNNのfinal stateをDecoder RNNのinitial stateとして設定し、Embeddingを入力する
Sampling：生成確率に基づいてトークンをランダムに選ぶ
Embedding：2で選ばれたトークンをEmbeddingとしてDecoder RNNへの入力とする
Detokenize：1-3を繰り返し、2で得られたトークンを文字列に直す

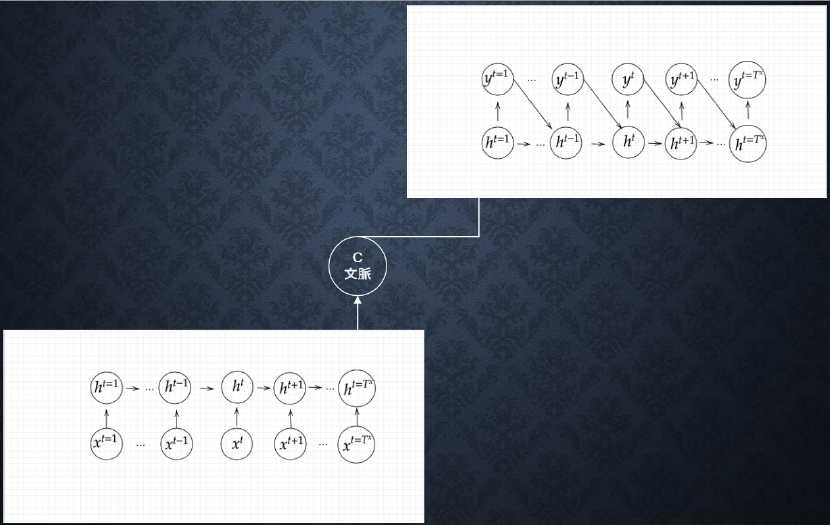
5-3. HRED

　__Seq2seq__は一問一答しかできず、問いに対して文脈も何もなくただ応答を行い続けるが、__HRED（エイチレッド）__は、過去n-1個の発話から次の発話を生成し、前の単語の流れに即して応答されるため、より人間らしい文章を生成することができる。
　__HRED__は、__Seq2seq+Context RNN__で構成されている。__Context RNN__とは、Encoderのまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する構造。つまり、過去の発話の履歴を加味した返答ができる。

HREDの課題：
同じコンテキストを与えられても、答えの内容が毎回会話の流れとしては同じものしか出せない
短いよくある答えを学ぶ傾向がある

5-4. VHRED

　__VHRED（ヴイエイチレッド）__とは、__HRED__の課題を__VAE__の潜在変数の概念を追加することで解決した構造。

5-5. オートエンコーダ

　__オートエンコーダ__とは、教師なし学習の一つ。入力データから潜在変数$z$に変換するニューラルネットワーク、__Encoder__と、潜在変数$z$をインプットとして元画像を復元するニューラルネットワーク、__Decoder__から構成されている。オートエンコーダのメリットは、潜在変数への変換で__次元削減__が行えることである。

具体例：MNISTの場合、28×28の数字の画像を入れて、同じ画像を出力するニューラルネットワークということになる。

5-6. VAE

　__オートエンコーダ__は、何かしらの潜在変数$z$にデータを入れているもののその構造がどのような状態がわからない。__VAE（Variational Autoencoder）__は、データを潜在変数$z$の確率分布N(0,1)という構造に入れることを実現できている。

Section6）Word2Svec

Word2vec：単語のような可変長の文字列をベクトルに表す
学習データからボキャブラリを作成→one-hotベクトル。ボキャブラリ数×単語ベクトルの次元数の重み行列→Embedding表現に変換
one-hotベクトルは要素数が多くなるため、Embedding表現に変換する

Section7）Attention Mechanism

seq2seqは長い文章への対応が困難。2単語でも100単語でも固定次元ベクトルの中に入力する必要がある。そこで、文章が長くなるほど、そのシーケンスの内部表現の次元も大きくなっていく仕組みを使ったものが、Attention Mechanismである。「入力と出力のどの単語が関連しているのか」の関連度を学習する仕組み。

2.「深層学習：Day3」確認テスト考察

★確認テスト1

サイズ5×5の入力画像を、サイズ3×3のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なお、ストライドは2、パディングは1とする。

解答

以下、公式を元に求める。


\begin{align}
〇順伝播&
高さ&= \frac{画像の高さ+2*パディング高さ-フィルター高さ}{ストライド}+1 \\
&=\frac{5+2*1-3}{2}+1 =3\\
幅&= \frac{画像の幅+2*パディング幅-フィルター幅}{ストライド}+1 \\
&=\frac{5+2*1-3}{2}+1 =3\\
\end{align}

求める出力画像のサイズは、3×3

★確認テスト2

RNNのネットワークには大きくわけて3つの重みがある。1つは入力から現在の中間層を定義する際にかけられる重み、1つは中間層から出力を定義する際にかけられる重みである。残りの1つの重みについて説明せよ。

解答

$W{in}$_：入力から現在の中間層を定義する際にかけられる重み
$W{out}$_：中間層から出力を定義する際にかけられる重み
$W$：前の中間層から現在の中間層を定義する際にかけられる重み

★確認テスト3

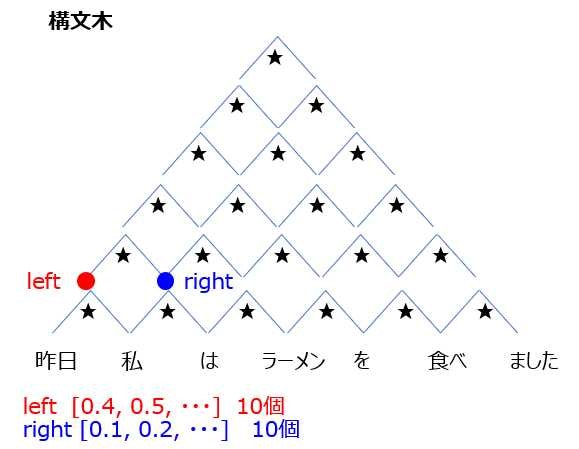
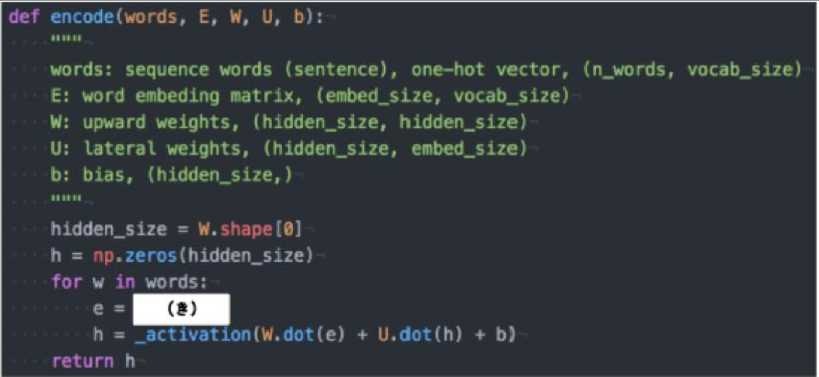
以下は再帰的ニューラルネットワークにおいて構造文木を入力として再帰的に文全体の表現ベクトルを得るプログラムである。ただし、ニューラルネットワークの重みパラメータはグローバル変数として定義してあるものとし、_activation関数はなんらかの活性化関数であるとする。木構造は最適な辞書で定義しており、__root__が最も外側の辞書であると仮定する。（く）にあてはまるのはどれか。

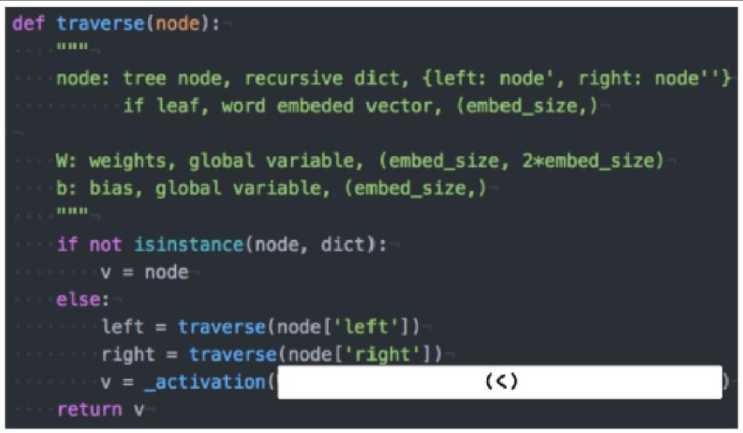
(1). W.dot(left + right)
(2). W.dot(np.concatenate([left, right]))
(3). W.dot(left * right)
(4). W.dot(np.maximum(left, right))

解答

まず、構文木とは・・・、

答えは
(2). W.dot(np.concatenate([left, right]))
left,__right__の各要素数を連結する。
left,__right__の特徴を生かすため。ただし、要素数がどんどん増えるため、特徴を生かしつつ、要素数を減らす工夫が必要。

(1),(3),(4)は__left__,right__のそれぞれの加算、乗算、Max値を求めても__left,__right__のそれぞれの特徴が消えてしまう。

★確認テスト4

連鎖律の原理を使い、$dz/dx$を求めよ。

$z = t^2$
$t = x + y$

解答


\begin{align}
\frac{dz}{dx} &= \frac{dz}{dt} \frac{dt}{dx} \\
&= \frac{d(t^2)}{dt} \frac{d(x + y)}{dx} \\
&= 2t * 1 = 2t\\
&= 2(x + y)\\
\end{align}

★確認テスト5

下の図は__BPTT__を行うプログラムである。なお簡単化のため活性化関数は恒等関数であるとする。また、__calculate_dout__関数は損失関数を出力に関して偏微分した値を返す関数であるとする。（お）にあてはまるのはどれか。

(1). delta_t.dot(W)
(2). delta_t.dot(U)
(3). delta_t.dot(V)
(4). delta_t*V

解答

答えは
(2). delta_t.dot(U)

RNNでは中間層出力$h_{t}$が過去の中間層出力である$h_{t-1}$,…,$h_{1}$に依存する。
RNNにおいて損失関数を重み$W$や$U$に関して偏微分するときは、それを考慮する必要があり、
$dh_{t}/dh_{t-1}=U$
であることに注意すると、過去に遡るたびに$U$が掛けられる。つまり、
$delta_t=delta_t.dot(U)である(2)が答えとなる。

★確認テスト6

RNNや深いモデルでは勾配の消失または爆発が起こる傾向がある。勾配爆発に勾配クリッピングを行うという手法がある。具体的には勾配のノルムがしきい値を超えたら、勾配のノルムをしきい値に正規化するというものである。以下は勾配のクリッピングを行う関数である。（さ）にあてはまるのはどれか。

(1). gradient * rate
(2). gradient / norm
(3). gradient / threshold
(4). np.maximum(gradient, threshold)

解答

答えは
(1). gradient * rate

勾配のノルムがしきい値より大きいときは、勾配のノルムをしきい値に正規化するので、クリッピングした勾配は、勾配×（しきい値/勾配のノルム）と計算される。つまり、gradient * rateである。

★確認テスト7

以下の文章を__LSTM__に入力し空欄に当てはまる単語を予測したいとする。文中の「とても」という言葉は空欄の予測においてなくなっても影響を及ぼさないと考えられる。このような場合、どのゲートが作用すると考えられるか。

「映画おもしろかったね。ところで、とてもお腹が空いたから何か・・・。」

(1). 入力ゲート
(2). 出力ゲート
(3). 忘却ゲート

解答

答えは
(3). 忘却ゲート

文中の「とても」という言葉が無くても文の意味は理解できる。その際、「とても」という言葉が出た場合、「忘却ゲート」にて忘れてしまっても構わないとのことから、答えは(3)となる。

★確認テスト8

以下のプログラムは__LSTM__の順伝播を行うプログラムである。ただし、_sigmoid関数は要素ごとにシグモイド関数を作用させる関数である。（け）にあてはまるのはどれか。

(1). output_gate * a + forget_gate * c
(2). forget_gate * a + output_gate * c
(3). input_gate * a + forget_gate * c
(4). forget_gate * a + input_gate * c

解答

答えは
(3). input_gate * a + forget_gate * c

__c__とは、今回CECが覚えている情報を表す関数であり、
以下式から求められる。今回の答えも以下式の通り(3)が選ばれる。


\begin{align}
c(t)=i(t)*a(t)+f(t)*c(t-1)
\end{align}

★確認テスト9

__LSTM__と__CEC__が抱える課題について、それぞれ簡潔に述べよ。

解答

LSTM：パラメータ数が多く計算量が多い
CEC：学習能力が無く周囲に学習させる必要がある。

★確認テスト10

GRU（Gated Recurrent Unit）もLSTMと同様にRNNの一種であり、単純なRNNにおいて問題となる勾配消失問題を解決し、長期的な依存関係を学習することができる。LSTMに比べ変数の数やゲートの数が小さく、より単純なモデルであるが、タスクによってはLSTMより良い性能を発揮する。以下のプログラムはGRUの順伝播を行うプログラムである。ただし、_sigmoid関数は要素ごとにシグモイド関数を作用させる関数である。（こ）に当てはまるのはどれか。

(1). z * h_bar
(2). (1-z) * h_bar
(3). z * h * h_bar
(4). (1-z) * h + z * h_bar

解答

答えは
(4). (1-z) * h + z * h_bar

★確認テスト11

__LSTM__と__GRU__の違いを簡潔に述べよ。

解答

LSTM：入力・出力・忘却ゲートやCECがある。パラメータが多く、計算量が多い。
GRU：CEC無し。リセット・更新ゲートのみ。LSTMに比べ、パラメータ数が少なく、計算量も少ない。

★確認テスト12

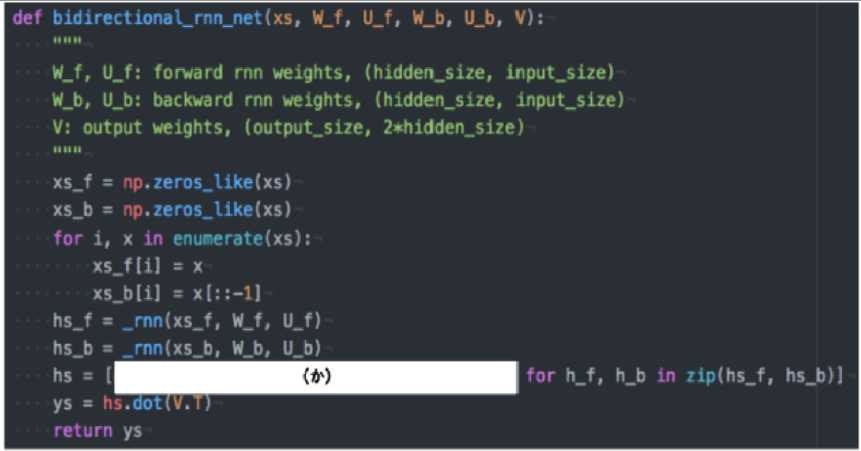
以下は、双方向RNNの順伝播を行うプログラムである。順方向については、入力から中間層への重みW_f一ステップ前の中間層出力から中間層への重みをU_f、逆方向に関しては同様にパラメータW_b、U_bを持ち、両者の中間層表現を合わせた特徴から出力層への重みはVである。_rnn関数はRNNの順伝播を表し中間層の系列を返す関数であるとする。（か）に当てはまるのはどれか。

(1). h_f + h_b[::-1]
(2). h_f * h_b[::-1]
(3). np.concatenate([h_f, h_b[::-1]], axis = 0)
(4). np.concatenate([h_f, h_b[::-1]], axis = 1)

解答

答えは
(4). np.concatenate([h_f, h_b[::-1]], axis = 1)

特徴量を失わないようにするために、"+"や"*"は用いない。また、過去、未来を同じ配列で並べるため、答えは(4)となる。

★確認テスト13

下記の選択肢から、__seq2seq__について説明しているものを選べ。

(1). 時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用するものである。
(2). RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
(3). 構文木などの木構造に対して、隣接単語から表現ベクトル（フレーズ）を作るという演算を再帰的に行い（重みは共通）、分全体の表現ベクトルを得るニューラルネットワークである。
(4). RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を導入することで解決したものである。

解答

答えは(2)

(1)は双方向RNNの説明、(3)は構文木の説明、(4)はLSTMの説明。

★確認テスト14

機械翻訳タスクにおいて、入力は複数の単語からなる文（文章）であり、それぞれの単語はone-hotベクトルで表現されている。Encoderにおいて、それらの単語は埋め込みにより特徴量に変換され、そこからRNNによって（一般にはLSTMを使うことが多い）時系列の情報を持つ特徴へとエンコードされる。以下は、入力である文（文章）を時系列の情報持つ特徴量へとエンコードする関数である。ただし、_activation関数はなんらかの活性化関数とする。（き）に当てはまるのはどれか。

(1). E.dot(w)
(2). E.T.dot(w)
(3). w.dot(E.T)
(4). E * w

解答

答えは
(1). E.dot(w)

単語wはone-hotベクトルであり、それを単語埋め込みにより別の特徴量に変換する。これは、埋め込み行列Eを用いて、E.dot(w)と書ける。

★確認テスト15

seq2seq__と__HRED、__HRED__と__VHRED__の違いを簡潔に述べよ。

解答

答え

seq2seq：一文の一問一答に対して処理ができる、ある時系列データからある時系列データを作り出すネットワーク
HRED：seq2seqの機構に、それまでの文脈の意味ベクトルを解釈に加えられるようにすることで、文脈の意味をくみ取った文のエンコードとデコードをできるようにしたもの
VHRED：HREDが文脈に対して当たり障りのない回答しか作れないのに対しての解決策。オートエンコーダ、VAEの考え方を取り入れて、短い、当たり障りのない単語以上の出力をだせるように改良を施したモデル。

★確認テスト16

RNN__と__word2vec、__seq2seq__と__Attention Mechanism__の違いを簡潔に述べよ。

解答

答え

RNN：時系列データを処理するのに適したニューラルネットワーク
word2vec：単語の分散表現ベクトルを得る手法
seq2seq：一つの時系列データから別の時系列データを得るネットワーク
Attention Mechanism：時系列データの中身に対して関連性に重みを付ける手法

3.「深層学習：Day3」実装演習結果と考察

3-1.RNN

3_1_simple_RNN_after.ipynbにてRNNについて理解、演習する。

今回は、8bitの2進数同士の加算をテーマにRNNの演習を実施する。

3-1-1.　importと関数定義

importと関数の定義を実施する。

使用するライブラリは__numpy__と__matplotlib__、そして別定義のfunctionsを読み込み。
関数は、活性化関数として、__tanh__の微分関数を定義している。

import numpy as np
from common import functions
import matplotlib.pyplot as plt

def d_tanh(x):
    return 1/(np.cosh(x) ** 2)

3-1-2.　係数設定

ここでは、各種係数の設定を実施している。__8bitの2進数__をbinary_dimで表している。そして、10進数での最大値をlargest_numberで表しており(0～255)、その際の2進数もbinaryで用意している。

RNN__の入力層（input_layer_size=2）、中間層（hidden_layer_size=16）、出力層（output_layer_size=1）の__レイヤ数、ウェイトの初期設定値（weight_init_std）、学習率（learning_rate）のネットワーク設定を実施。
また、学習繰り返し数としてiters_numを__10000__に、学習結果表示のインターバルとしてplot_intervalを__100__に設定している。

# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)

input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1

weight_init_std = 1
learning_rate = 0.1

iters_num = 10000
plot_interval = 100

3-1-3.　ウェイト、各関数の初期設定

ここでは、ウェイトおよび、各層の入出力等の関数の初期設定を実施している。ウェイトは、weight_init_std=1とし、__Xavier__や__He__の重みの初期設定は今回は未実施。各関数も__0__で設定している。

# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)

# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)

u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))

delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))

all_losses = []

3-1-4.　学習開始

ここから学習が開始される。繰り返し変数iters_numのforループがスタート。
繰り返されるごとに0～127までの数a,bをランダムに設定。ランダムに設定された10進数とその2進数、a,bの加算値dの10進数と2進数をそれぞれ用意。2進数は、8桁の0,1データで設定している。また、出力バイナリとして、予測結果の値が入れられるout_binを用意。

for i in range(iters_num):
    
    # A, B初期化 (a + b = d)
    a_int = np.random.randint(largest_number/2)
    a_bin = binary[a_int] # binary encoding
    b_int = np.random.randint(largest_number/2)
    b_bin = binary[b_int] # binary encoding
    
    # 正解データ
    d_int = a_int + b_int
    d_bin = binary[d_int]
    
    # 出力バイナリ
    out_bin = np.zeros_like(d_bin)
    
    # 時系列全体の誤差
    all_loss = 0

3-1-5.　時系列ループ＋順伝播

時系列ループとして、8桁の2進数の1桁ごとをループにしている。ここでは順伝播の設定を実施、中間層と出力層の活性化関数には、__シグモイド関数__を設定。時系列ループのため、forループのtとt+1が関数u,z,yに作用されている。

    # 時系列ループ
    for t in range(binary_dim):
        # 入力値
        X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
        # 時刻tにおける正解データ
        dd = np.array([d_bin[binary_dim - t - 1]])
        
        u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
        z[:,t+1] = functions.sigmoid(u[:,t+1])
        y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))

        #誤差
        loss = functions.mean_squared_error(dd, y[:,t])
        
        delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])   
        
        all_loss += loss

        out_bin[binary_dim - t - 1] = np.round(y[:,t])

3-1-6.　誤差逆伝播

誤差逆伝播として、中間層での$\delta^t$、出力層での$\delta^{out,t}$をそれぞれ設定し、誤差逆伝播で勾配更新を実施。

    for t in range(binary_dim)[::-1]:
        X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)        

        delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])    

        # 勾配更新
        W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
        W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
        W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
    
    # 勾配適用
    W_in -= learning_rate * W_in_grad
    W_out -= learning_rate * W_out_grad
    W -= learning_rate * W_grad
    
    W_in_grad *= 0
    W_out_grad *= 0
    W_grad *= 0

3-1-7.　結果表示設定＋グラフ設定

最後は、学習結果表示のインターバルとして設定したplot_intervalに沿ってのprint文設定と、__matplotlib__のグラフ設定を実施。

今回の__Loss__は、8桁の各bitのLossを加算したall_lossを表記している。

    if(i % plot_interval == 0):
        all_losses.append(all_loss)        
        print("iters:" + str(i))
        print("Loss:" + str(all_loss))
        print("Pred:" + str(out_bin))
        print("True:" + str(d_bin))
        out_int = 0
        for index,x in enumerate(reversed(out_bin)):
            out_int += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
        print("------------")

lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()

3-1-8.　学習結果

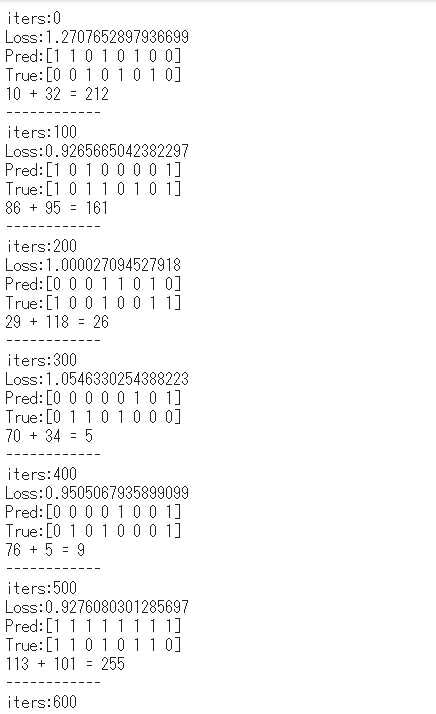
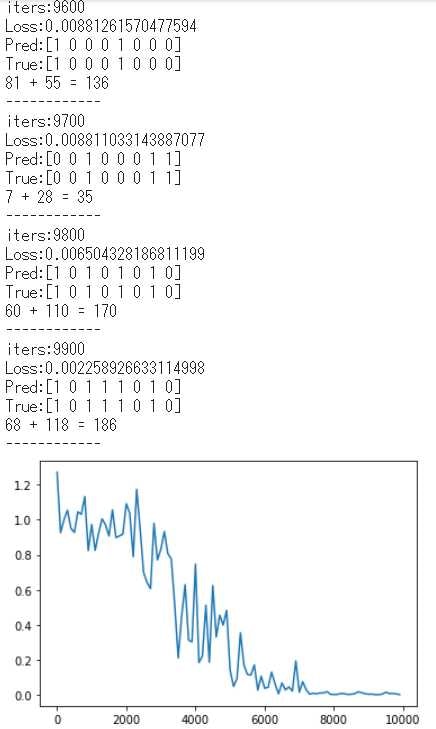
学習結果が以下である。

学習開始時点では、予測結果Predと正解データTrueがアンマッチとなっているが、学習が進むにつれて、__Loss__が小さくなり予測結果と正解データが一致していっているのがわかる。

時系列データの学習として、過去データ（隣のbit）も含め学習させていくRNNの演習となった。

・・・

3-2.RNN-2

3_3_predict_sin.ipynbにてRNNについて理解、演習する。

今回は、SIN波データの予測をテーマにRNNの演習を実施する。

3-2-1.　importとSIN波曲線定義

importと関数の定義を実施する。

使用するライブラリは__numpy__と__matplotlib__、sklearn__そして別定義のfunctionsを読み込み。ランダム値は、ランダムシード設定により、毎回同じランダム値を呼び出している。そして、SIN波用の時間軸__ts、SIN波__f__を定義している。
　今回の時系列データはSIN波の時間軸とし、一つの時系列のデータの長さをmaxlen = 2と設定し、入力データとして、先ほど定義したSIN波__f__の時間軸2データ分としている。

import numpy as np
from common import functions
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

np.random.seed(0)

# sin曲線
round_num = 10
div_num = 500
ts = np.linspace(0, round_num * np.pi, div_num)
f = np.sin(ts)

# ひとつの時系列データの長さ
maxlen = 2

# sin波予測の入力データ
test_head = [[f[k]] for k in range(0, maxlen)]

data = []
target = []

3-2-2.　学習データ、正解データ、係数設定

ここでは、学習データ、正解データ及び各種係数の設定を実施している。dataには学習用データとして、長さ2のSIN波データ（i=0時、i=0,1のSIN波データ）を、正解データとして長さ2の時系列後のSIN波データ（i=0時、i=2のSIN波データ）を設定している。

RNN__の入力層（input_layer_size=1）、中間層（hidden_layer_size=5）、出力層（output_layer_size=1）の__レイヤ数、ウェイトの初期設定値（weight_init_std）、学習率（learning_rate）のネットワーク設定を実施。
また、学習繰り返し数としてiters_numを__500__に設定している。

for i in range(div_num - maxlen):
    data.append(f[i: i + maxlen])
    target.append(f[i + maxlen])
    
X = np.array(data).reshape(len(data), maxlen, 1)
D = np.array(target).reshape(len(data), 1)

# データ設定
N_train = int(len(data) * 0.8)
N_validation = len(data) - N_train

x_train, x_test, d_train, d_test = train_test_split(X, D, test_size=N_validation)

input_layer_size = 1
hidden_layer_size = 5
output_layer_size = 1

weight_init_std = 0.01
learning_rate = 0.1

iters_num = 500

3-2-3.　ウェイト、各関数の初期設定

ここでは、ウェイトおよび、各層の入出力等の関数の初期設定を実施している。ウェイトは、weight_init_std=0.01とし、__Xavier__や__He__の重みの初期設定は今回未実施。各関数も__0__で設定している。

# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)

# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)

us = []
zs = []

u = np.zeros(hidden_layer_size)
z = np.zeros(hidden_layer_size)
y = np.zeros(output_layer_size)

delta_out = np.zeros(output_layer_size)
delta = np.zeros(hidden_layer_size)

losses = []

3-2-4.　学習開始+順伝播

ここから学習が開始される。繰り返し変数iters_numのforループがスタート。
繰り返し学習されるデータは、div_num=500の0.8倍である400のx_trainとd_trainデータ。時系列ループには、x_trainに保存されている、各時間軸における2データ分をループしている。中間層と出力層の活性化関数には、それぞれ__tanh関数__と__恒等写像__を設定。

# トレーニング
for i in range(iters_num):
    for s in range(x_train.shape[0]):
        us.clear()
        zs.clear()
        z *= 0
        
        # sにおける正解データ
        d = d_train[s]

        xs = x_train[s] 

        # 時系列ループ
        for t in range(maxlen):
            
            # 入力値
            x = xs[t]
            u = np.dot(x, W_in) + np.dot(z, W)
            us.append(u)
            z = np.tanh(u)
            zs.append(z)

        y = np.dot(z, W_out)
        
        #誤差
        loss = functions.mean_squared_error(d, y)
        
        delta_out = functions.d_mean_squared_error(d, y)
        
        delta *= 0

3-2-5.　誤差逆伝播

誤差逆伝播として、中間層での$\delta^t$、出力層での$\delta^{out,t}$をそれぞれ設定し、誤差逆伝播で勾配更新を実施。

        for t in range(maxlen)[::-1]:
            
            delta = (np.dot(delta, W.T) + np.dot(delta_out, W_out.T)) * d_tanh(us[t])
            
            # 勾配更新
            W_grad += np.dot(zs[t].reshape(-1,1), delta.reshape(1,-1))
            W_in_grad += np.dot(xs[t], delta.reshape(1,-1))
        W_out_grad = np.dot(z.reshape(-1,1), delta_out)
        
        # 勾配適用
        W -= learning_rate * W_grad
        W_in -= learning_rate * W_in_grad
        W_out -= learning_rate * W_out_grad.reshape(-1,1)
            
        W_in_grad *= 0
        W_out_grad *= 0
        W_grad *= 0

3-2-6.　テストデータによる検証

　ここでは、先ほど学習した重みを用い、残りの__100__データで、テストデータによる予測を行う。結果表示は、このテストデータによるLoss、正解データd、予測データyを表示する。

# テスト        
for s in range(x_test.shape[0]):
    z *= 0

    # sにおける正解データ
    d = d_test[s]

    xs = x_test[s]

    # 時系列ループ
    for t in range(maxlen):

        # 入力値
        x = xs[t]
        u = np.dot(x, W_in) + np.dot(z, W)
        z = np.tanh(u)

    y = np.dot(z, W_out)

    #誤差
    loss = functions.mean_squared_error(d, y)
    print('loss:', loss, '   d:', d, '   y:', y)

3-2-7.　結果表示設定＋グラフ設定

最後は、pred_numで設定した数のSIN波データ予測とSIN波グラフ表示を実施。

original = np.full(maxlen, None)
pred_num = 200

xs = test_head

# sin波予測
for s in range(0, pred_num):
    z *= 0
    for t in range(maxlen):
        
        # 入力値
        x = xs[t]
        u = np.dot(x, W_in) + np.dot(z, W)
        z = np.tanh(u)

    y = np.dot(z, W_out)
    original = np.append(original, y)
    xs = np.delete(xs, 0)
    xs = np.append(xs, y)

plt.figure()
plt.ylim([-1.5, 1.5])
plt.plot(np.sin(np.linspace(0, round_num* pred_num / div_num * np.pi, pred_num)), linestyle='dotted', color='#aaaaaa')
plt.plot(original, linestyle='dashed', color='black')
plt.show()

3-2-8.　学習結果

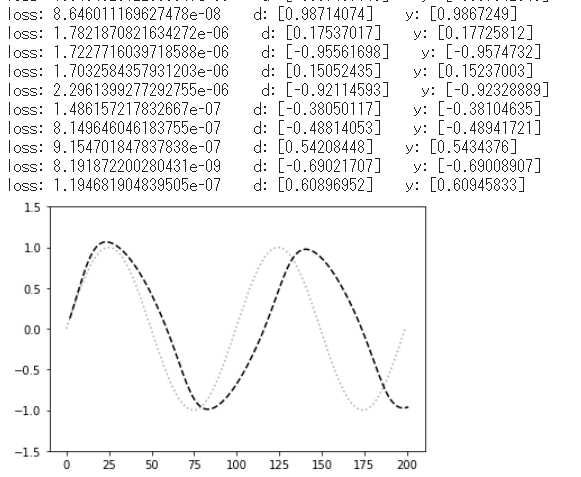
学習結果が以下である。

今回の学習結果は、学習済みの重みに対してのテストデータによる__loss__表示のため、全100データ全て非常に小さい値となっており、また、正解データに対する予測データもほぼ同値となっている。

グラフ表示は、学習済みの重みに対し、時間軸2データ分置きにデータを予測しているグラフだが、ほぼSIN波が再現されている結果となった。時間を重ねるごとにズレが大きくなっている点、学習が不足していると思われる結果となっている。

・・・

###関連ページ

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

ディープラーニング講座「深層学習：Day3」要点まとめ＆実装演習

1.「深層学習：Day3」講義動画の要点まとめ

Section1）再帰型ニューラルネットワークの概念

Section2）LSTM

Section3）GRU

Section4）双方向RNN

Section5）Seq2Seq

5-1. Encoder RNN

5-2. Decoder RNN

5-3. HRED

5-4. VHRED

5-5. オートエンコーダ

5-6. VAE

Section6）Word2Svec

Section7）Attention Mechanism

2.「深層学習：Day3」確認テスト考察

3.「深層学習：Day3」実装演習結果と考察

3-1.RNN

3-1-1. importと関数定義

3-1-2. 係数設定

3-1-3. ウェイト、各関数の初期設定

3-1-4. 学習開始

3-1-5. 時系列ループ＋順伝播

3-1-6. 誤差逆伝播

3-1-7. 結果表示設定＋グラフ設定

3-1-8. 学習結果

3-2.RNN-2

3-2-1. importとSIN波曲線定義

3-2-2. 学習データ、正解データ、係数設定

3-2-3. ウェイト、各関数の初期設定

3-2-4. 学習開始+順伝播

3-2-5. 誤差逆伝播

3-2-6. テストデータによる検証

3-2-7. 結果表示設定＋グラフ設定

3-2-8. 学習結果