ディープラーニング講座「機械学習」実装演習

私は、2020年7月に「G検定（2020 #2）」に合格した。
次は、2021年2月実施の「E資格（2021 #1）」受験資格である__JDLA認定プログラム「３カ月で現場で潰しが効くディープラーニング講座」__に2020年8月から挑戦中。

本記事では、__JDLA認定プログラム「3カ月で現場で潰しが効くディープラーニング講座」の課題であり、「機械学習」__実装演習結果をまとめる。

1.　線形回帰モデル

1-1.　課題

ボストンの住宅価格データから、以下3条件を満たす物件はいくらになるかを予測する
　・犯罪発生率：0.3件／人口単位
　・部屋数：4部屋
　・1940年よりも前に建てられた家屋の割合：50%

※3変数の線形重回帰分析

1-2.　実装演習

1-2-1.　必要モジュールとデータのインポート

#from モジュール名 import クラス名（もしくは関数名や変数名）
from sklearn.datasets import load_boston
from pandas import DataFrame
import numpy as np

# ボストンデータを"boston"というインスタンスにインポート
boston = load_boston()

読み込むライブラリは、sklearn、pandas、__numpy__の3つ。
__sklearn__は、ボストン住宅価格データを読み込むため、__pandas__は、データを表形式で扱えるライブラリで、データを扱いやすくするため、__numpy__は、行列演算を効率的に行うために利用する。

1-2-2.　インポートデータの確認

#インポートしたデータを確認(data / target / feature_names / DESCR)
print(boston)

bostonというインスタンスにインポートしたデータをprint()で確認する。

確認したデータは以下。

1-2-3.　データフレームの作成

#　説明変数らをDataFrameへ変換
df = DataFrame(data=boston.data, columns = boston.feature_names)

# 目的変数をDataFrameへ追加
df['PRICE'] = np.array(boston.target)

bostonデータの説明変数を__DataFrame__に変換。行：boston.data、列：boston.feature_names。
また、目的変数も__DataFrame__に追加。行：boston.target、列：「PRICE」。

変換した__DataFrame__は以下のように格納される。

以上で、ボストンデータ内の説明変数、目的変数を__pandas__の__DataFrame__に格納できた。

1-2-4.　線形重回帰分析（3変数）

まずは、今回分析に使うデータを詳しく見てみよう。

• 犯罪発生率[件/人口単位]：　CRIM
• 部屋数[部屋]：　RM
• 1940年よりも前に建てられた家屋の割合[%]：　AGE
• 住宅価格[*1000ドル]：　PRICE

#カラムを指定してデータを表示
df[['CRIM', 'RM', 'AGE', 'PRICE']]

506の住宅価格データがあるため、この表だけ見ても各説明変数や目的変数の大きさがわかりにくい。そこで、各変数データの最大値、平均値等の集計結果を見てみる。

#指定データの集計結果（平均、Max、Minなど）
df[['CRIM', 'RM', 'AGE', 'PRICE']].describe()

この集計結果により、データ全体を大まかに掴めることができた。

次に、線形重回帰分析の準備に入る。
__DataFrame__から必要なデータを変数data3とtarget3に入れる。

# 説明変数
data3 = df.loc[:, ['CRIM', 'RM', 'AGE']].values
# 目的変数
target3 = df.loc[:, 'PRICE'].values

説明変数は3種類を1変数に入れるため、合わせてどのようにdata3に格納されているか見てみよう。

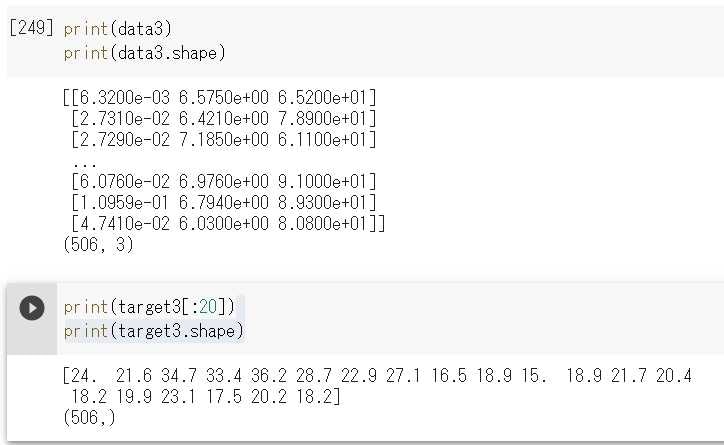
上記結果より、説明変数data3は506行3列、目的変数target3は506個のデータとなっている。説明変数のデータがどのように配置されているかは、上記の__DataFrame__を表示したデータと見比べるとわかるだろう。

さて、いよいよ線形重回帰分析に入る。
__sklearn__モジュールから__LinearRegression__をインポートし、線形回帰モデルmodel3を作る。

## sklearnモジュールからLinearRegressionをインポート
from sklearn.linear_model import LinearRegression

# オブジェクト生成
model3 = LinearRegression()
model3.get_params()

線形回帰モデルを作成したら、説明変数data3、目的変数target3を指定し、線形回帰分析を行う。

# fit関数でパラメータ推定
model3.fit(data3, target3)

以上で求めたい線形回帰分析ができた。
求めたい住宅価格をおさらいしよう。

ボストンの住宅価格データから、以下3条件を満たす物件はいくらになるかを予測する
　・犯罪発生率：0.3件／人口単位
　・部屋数：4部屋
　・1940年よりも前に建てられた家屋の割合：50%

上記3条件を満たす住宅価格の予測結果は、以下のように5.85[*1000ドル]となった。

1-2-5.　回帰係数と切片の値を確認

もう少し続けてみよう。

今回の線形重回帰分析でどのような回帰係数や切片となったのかを確認してみる。

この回帰係数や切片は、CRIM、RM、__AGE__から__PRICE__を導き出す計算式の係数である。
具体的な計算式は以下である。

PRICE = model3.intercept_ + CRIM * model3.coef[0]_ + RM * model3.coef[1]_ + AGE * model3.coef[2]_

検証結果も合わせて確認し、同じ結果となることを確認できた。

2.　非線形回帰モデル

2-1.　課題

ある非線形関数からノイズを伴うデータを生成し、複数の回帰モデルを用い学習する。

• 非線形関数:　

　1-48*x+218*x^2-315*x^3+140*x^4

• データ数:　n=200
• 回帰モデル:　LinearRegression、KernelRidge、Ridge

2-2.　実装演習

2-2-1.　必要モジュールのインポート

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

読み込むライブラリは、numpy、matplotlib、__seaborn__の3つ。
__seaborn__は、__matplotlib__同様、データの可視化するライブラリ。__seaborn__は、統計データや観測データをより簡単に美しく可視化することができるライブラリである。

2-2-2.　seabornによるグラフの設定

#seaborn設定
sns.set()
#背景変更
sns.set_style("whitegrid", {'grid.linestyle': '--'})
#sns.set_style("darkgrid") #デフォルト
#sns.set_style("whitegrid")
#sns.set_style("dark")
#sns.set_style("white")
#sns.set_style("ticks")
#sns.set_style("ticks despine")
#大きさ(スケール変更)
#sns.set_context("paper")
sns.set_context("notebook") #デフォルト
#sns.set_context("talk")
#sns.set_context("poster")

__seaborn__で可視化するグラフの背景やグリッド有無、グラフのスケールを設定している。

2-2-3.　非線形関数からノイズを伴うデータを生成

以下の非線形関数をpythonで実装する。

　1-48*x+218*x^2-315*x^3+140*x^4

def true_func(x):
    z = 1-48*x+218*x**2-315*x**3+140*x**4
    return z 

次に非線形関数からノイズを伴うデータを生成する。

# 真の関数からノイズを伴うデータを生成
n=200

# 真の関数からデータ生成
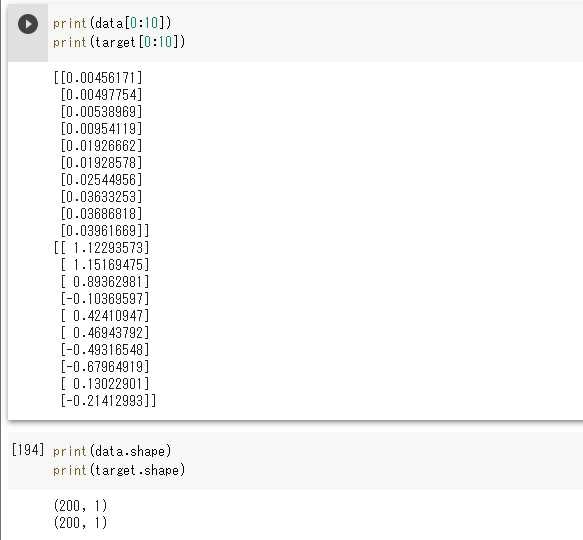
data = np.random.rand(n).astype(np.float32)
data = np.sort(data)
target = true_func(data)

# 　ノイズを加える
noise = 0.5 * np.random.randn(n) 
target = target  + noise

# ノイズ付きデータを描画

plt.scatter(data, target)

以下が生成したデータである。

2-2-4.　データの整形

上記にて作成したdata、targetは各__n=200__の__1次元の配列__となっている。

そのデータを機械学習をさせるため、__200行1列の2次元の配列__に整形する。

# data,target　データの整形
data = data.reshape(-1,1)
target = target.reshape(-1,1)

2-2-5.　LinearRegression

1つ目は__LinearRegression__で学習する。
__sklearn__ライブラリを用い、以下の数行でdata、targetに対し学習完了。

#LinearRegression
from sklearn.linear_model import LinearRegression

clf_lr = LinearRegression()
clf_lr.fit(data, target)

p_lr = clf_lr.predict(data)

後で、複数モデルの学習結果との差別化、1つのグラフ表記のため、clf_lr、p_lrはユニークな名前に設定。

2-2-6.　KernelRidge

2つ目は__KernelRidge__で学習する。
__KernelRidge__の設定パラメータには、alphaとgammaがある。
今回は、正則化（過学習しないよう抑える働き）の強度を決めるalphaのみを設定し、学習。

#KernelRidge
from sklearn.kernel_ridge import KernelRidge

clf_kr = KernelRidge(alpha=0.0002, kernel='rbf')
clf_kr.fit(data, target)

p_kr = clf_kr.predict(data)

2-2-7.　Ridge

最後は__Ridge__で学習する。
__Ridge__の設定には、リッジ正則化とガウス型基底関数を用いて学習。

#Ridge
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Ridge

kx = rbf_kernel(X=data, Y=data, gamma=50)

clf_r = Ridge(alpha=30)
clf_r.fit(kx, target)

p_r = clf_r.predict(kx)

2-2-8.　グラフ表記

今回は3つの回帰モデル__LinearRegression__、KernelRidge、__Ridge__にて非線形データにて学習を実施した。その結果をグラフに示す。

上記にて各モデルの学習結果はユニークに設定しているので、それぞれの結果に対し、__matplotlib__の設定をする。

#グラフ表記
plt.scatter(data, target, color='blue', label='data')
plt.plot(data, p_lr, color='darkorange', marker='', linestyle='-', linewidth=2, markersize=6, label='linear regression')
plt.plot(data, p_kr, color='green', marker='', linestyle='-', linewidth=2, markersize=6, label='kernel ridge')
plt.plot(data, p_r, color='purple', marker='', linestyle='-', linewidth=2, markersize=3, label='ridge regression')
plt.legend()

下のデータに対し、各学習済モデルの結果がグラフに併記された。
グラフを見てわかるように、dataに対し、線形回帰モデルの__LinearRegression__では、__未学習__状態となっているのが一目でわかる。

2-2-9.　各学習モデルにおける　決定係数（R^2）スコア

最後に各学習済みのモデルに対し__決定係数（$R^2$）__による評価を行ってみる。__決定係数（$R^2$）__では、推定されたモデルの当てはまりの良さ（度合い）を示すことができる。0から1までの値を取り、1に近いほど、モデルが実際のデータに当てはまっていることを表し、説明変数が目的変数を説明しているかがわかる指標となっている。

print("*** 各モデルにおける R^2 SCORE")
print("linear regression : ",clf_lr.score(data, target))
print("kernel ridge      : ",clf_kr.score(data, target))
print("ridge regression  : ",clf_r.score(kx, target))

上記$R^2$スコアと、グラフを見ると、よりデータに沿った学習となっているのは__KernelRidge__と言える。

今回は、テストデータのみでの学習となり、未知データによる検証を行っていないため、この結果から__KernelRidge__が一番良いモデルとの判断はできない。
しかし、規則性の無いデータに対しても非線形回帰モデルにて学習できることがわかった。

3.　ロジスティック回帰モデル

3-1.　課題

タイタニックの乗客データより、以下の指標から、「年齢が30歳の男性客は生き残れるか」、予測する
　・年齢
　・乗客の社会階級
　・性別

※3指標を分け3次元グラフにて確認

3-2.　実装演習

3-2-1.　必要モジュールとデータのインポート

#from モジュール名 import クラス名（もしくは関数名や変数名）
import pandas as pd
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

#matplotlibをinlineで表示するためのおまじない (plt.show()しなくていい)
%matplotlib inline

# titanic data csvファイルの読み込み
titanic_df = pd.read_csv('/content/drive/My Drive/study_ai_ml/data/titanic_train.csv')

読み込むライブラリは、matplotlib、seaborn、pandas、__numpy__の4つ。
また、__sklearn__は、後程読み込むため、ここでは未記載。

データは、支給されたcsvファイルを読み込んでいる。

3-2-2.　インポートデータの確認

# ファイルの先頭部を表示し、データセットを確認する
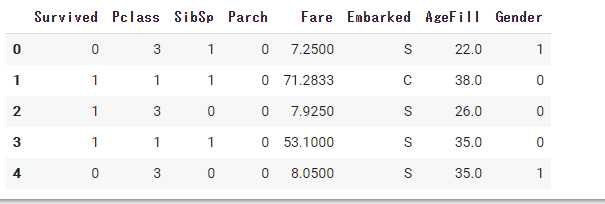
titanic_df.head(5)

titanic_dfというインスタンスにインポートしたデータを確認する。

確認したデータは以下。

3-2-3.　不要なデータの削除・欠損値の補完

#不要データの削除
titanic_df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)

#nullを含んでいる行を表示
titanic_df[titanic_df.isnull().any(1)].head(10)

#Ageカラムのnullを中央値で補完
titanic_df['AgeFill'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())

今回使用しないtitanic_df内のPassengerId、Name、Ticket、Cabinデータを削除。

また、Ageに欠損値__NaN__が存在しているため、欠損値__NaN__にAgeの全データの平均値を入力した、新しいAgeFillを追加。

以上、不要なデータの削除・欠損値の補完が完了。

3-2-4.　不要なデータの削除・データの加工

現状のデータを見てみる。

今回利用するデータは、以下の4種類のみ。

• 生存・死者情報：Survived（1:生存者/0:死者）
• 乗客の社会階級：Pclass（1:High/2:Middle/3:Low）
• 性別：Sex（Female:女性,Male:男性）
• 年齢：AgeFill（欠損値補完データ）

まだ不要なデータや問題が残っている。

まずは、性別を__文字列__から0,1に加工、追加し、不要データを削除する

#Columns 'Gender'追加
titanic_df['Gender'] = titanic_df['Sex'].map({'female': 0, 'male': 1}).astype(int)

#不要データの削除
titanic_df = titanic_df.drop(['Sex', 'Age'], axis=1)

まだ、不要なデータは残っているが、必要なデータは準備できたため、このデータでロジスティック解析を始める。

3-2-5.　ロジスティック回帰分析

ロジスティック回帰分析に入る前に、データを3次元グラフにて表し確認してみる。

from mpl_toolkits.mplot3d import Axes3D

index_survived = titanic_df[titanic_df["Survived"]==1].index #生存:1
index_notsurvived = titanic_df[titanic_df["Survived"]==0].index #死者:0

X1= titanic_df.loc[index_survived, 'AgeFill']
Y1= titanic_df.loc[index_survived, 'Pclass']
Z1= titanic_df.loc[index_survived, 'Gender']
X2= titanic_df.loc[index_notsurvived, 'AgeFill']
Y2= titanic_df.loc[index_notsurvived, 'Pclass']
Z2= titanic_df.loc[index_notsurvived, 'Gender']

# グラフの枠を作成
fig = plt.figure()
ax = Axes3D(fig)

# .plotで描画
ax.plot(X1,Y1,Z1,marker="o",linestyle='None',color='b', label='Survived', alpha=0.3)
ax.plot(X2,Y2,Z2,marker="o",linestyle='None',color='r', label='Not Survived', alpha=0.3)

ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass')
ax.set_zlabel('Gender')

ax.view_init(elev=20,azim=200)

# 最後に.show()を書いてグラフ表示
plt.legend()
plt.show()

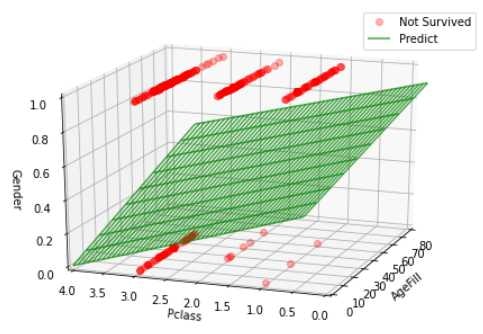
グラフ化の詳細は割愛する。上記設定で描画したグラフは以下である。

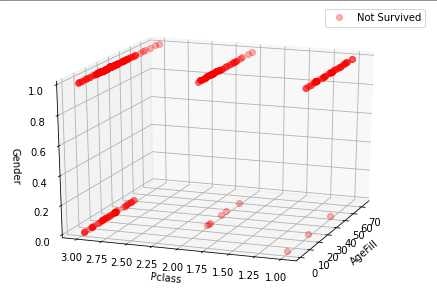
上記設定では生存・死者グラフは重なって描画されるが、データが重なって見にくいため、あえて分けてグラフを表示させた。

このグラフを一目見ても分かるように、Z軸の性別（0:女性、1:男性）を見ると、生存者は女性が多いことが分かった。また、死者の女性はPclass=3である低級階級の女性が多く無くなっていることがわかる。

さて、いよいよロジスティック回帰分析を始める。

#年齢、社会階級、性別だけのリストを作成
xdata = titanic_df.loc[:, ["AgeFill", "Pclass", "Gender"]].values
xdata

#生死フラグのみのリストを作成
tlabel =  titanic_df.loc[:,["Survived"]].values

上記のように説明変数、目標変数それぞれのリストを作成し、__sklearn__で学習させる。

from sklearn.linear_model import LogisticRegression

model = LogisticRegression()

model.fit(xdata, tlabel)

学習が終わったら、以下の条件での生存の確率を予想してみる。

• 年齢（AgeFill）：30歳
• 社会階級（Pclass）：高級階級（1）
• 性別（Gender）：男性

#予測結果  <NotSurvived:0/Survived:1>
#  [AgeFill, Pclass(High:1/Middle:2/Low:3), Gender(Female:0/Male:1)]
#  [0(NotSurvived)の確率, 1(Survived)の確率]
model.predict_proba([[30,1,1]])

3-2-6.　回帰係数と切片の値を確認

もう少し続けてみよう。

今回のロジスティック回帰分析でどのような回帰係数や切片となったのかを確認してみる。

ここで求めた回帰係数、切片を元に前述した3Dグラフに回帰平面を描いてみよう。

from mpl_toolkits.mplot3d import Axes3D

x = np.arange(0,80,0.01)
z = np.arange(0,1,0.1)

XP, ZP = np.meshgrid(x, z)

YP= (-model.intercept_[0] - model.coef_[0][0]*XP - model.coef_[0][2]*ZP) / model.coef_[0][1]

index_survived = titanic_df[titanic_df["Survived"]==1].index #生存:1
index_notsurvived = titanic_df[titanic_df["Survived"]==0].index #死者:0

X1= titanic_df.loc[index_survived, 'AgeFill']
Y1= titanic_df.loc[index_survived, 'Pclass']
Z1= titanic_df.loc[index_survived, 'Gender']
X2= titanic_df.loc[index_notsurvived, 'AgeFill']
Y2= titanic_df.loc[index_notsurvived, 'Pclass']
Z2= titanic_df.loc[index_notsurvived, 'Gender']

# グラフの枠を作成
fig = plt.figure()
ax = Axes3D(fig)

# .plotで描画
ax.plot(X1,Y1,Z1,marker="o",linestyle='None',color='b', label='Survived', alpha=0.3)
ax.plot(X2,Y2,Z2,marker="o",linestyle='None',color='r', label='Not Survived', alpha=0.3)
ax.plot_wireframe(XP, YP, ZP,color='g', label='Predict', alpha=0.7)

ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass')
ax.set_zlabel('Gender')
ax.set_xlim(0, 80)
ax.set_ylim(0, 4)
ax.set_zlim(0, 1)

ax.view_init(elev=20,azim=200)

# 最後に.show()を書いてグラフ表示
plt.legend()
plt.show()

平面を表現する角度調節は難しかったが、うまく表現することができた。
ですが、グラフで表現できるのは3次元が限界となる。

今回選定した説明変数でのロジスティック回帰分析では、上手に分類できている結果とは言えない結果となったが、この考え方を元にすれば説明変数の次元を増やし分析することも可能だろう。

4.　主成分分析

4-1.　課題

乳がん検査データより、32次元のデータを2次元上に次元圧縮した際にうまく判別できるかを確認する。

4-2.　実装演習

4-2-1.　必要モジュールとデータのインポート

#from モジュール名 import クラス名（もしくは関数名や変数名）
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
%matplotlib inline

# cancer data csvファイルの読み込み
cancer_df = pd.read_csv('/content/drive/My Drive/study_ai_ml/data/cancer.csv')

読み込むライブラリは、pandas、sklearn、__matplotlib__の3つ。その中でも__sklearn__は、複数のモジュールをインポートしている。以降でそれぞれを説明していく。

また、データは、支給されたcsvファイルを読み込んでいる。

4-2-2.　インポートデータの確認

今回の実践演習は32次元のデータを扱い、主成分分析により次元圧縮する演習である。まずは、cancer_dfというインスタンスにインポートしたデータの次元数を確認し、合わせてデータの中身を確認しよう。

print('cancer df shape: {}'.format(cancer_df.shape))

cancer_dfを見ると、0～568の569人の個人データおよびidや診断結果diagnosisを含む、検査データが32列に渡り並んでいることがわかる。今回はこれらのデータを活用しロジスティック回帰分析と主成分分析を行っていく。

4-2-3.　目的変数と説明変数の抽出

まずは目的変数を抽出する。

# 目的変数の抽出
y = cancer_df.diagnosis.apply(lambda d: 1 if d == 'M' else 0)

この記述ではデータの置き換えをしながら目的変数の抽出をしている。

置き換え前後のdiagnosisデータを見てみると、データMが1に、Bが0に置き換え変数yに抽出されていることがわかる。
ちなみに、診断結果diagnosisのM(1)は__悪性__、B(0)は__良性__を示している。

次に説明変数を抽出する。

# 説明変数の抽出
X = cancer_df.loc[:, 'radius_mean':]

この記述では行の個人データ数は加工せず、列のradius_mean以降のデータを抽出している。569人データ×idと診断結果diagnosisを除く30の検査データが説明変数‘X`に抽出できた。

4-2-4.　学習用、テスト用データ分離とデータの標準化

抽出した目的変数yと説明変数Xを__sklearn__の__train_test_split__モジュールで学習用、テスト用に分離する。

# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

random_stateは乱数生成のシードとなる整数の指定で、指定しない場合は、実行する度に抽出データが変わる。学習用、テスト用データサイズは指定していないのでデフォルト7.5:2.5で分割される。

次にデータの標準化を行う。
抽出したX_testを見てみると、各検査データの値がバラバラでこれらを同基準での分析をするのは困難。

そこで、以下の記述でデータを標準化する。

# 標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

標準化後の実際のデータは以下のようになる。

標準化前後のデータ比較のため、__pandas__の__DataFrame__化してデータを見てみる。

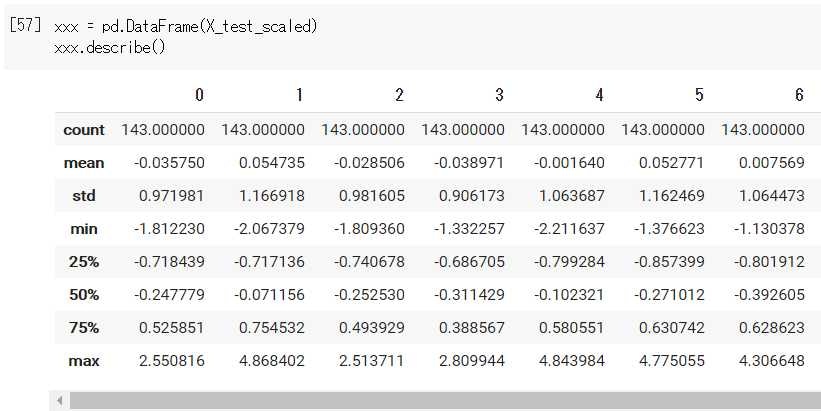
すると、平均meanが__0__、標準偏差stdが__1__となるデータに標準化することができた。

4-2-5.　ロジスティック回帰分析

標準化した説明変数X_train_scaledと目的変数y_trainでロジスティック回帰分析を行い、学習データ、テストデータによる検証結果を見てみる。

# ロジスティック回帰で学習
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_scaled, y_train)

# 検証
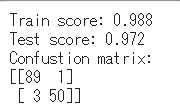
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))

学習データ、テストデータの検証結果はそれぞれ98.8%,97.2%で分類できている。また、クラス分類の精度を評価するための、混同行列 （Confusion matrix）の指標で見てみると、以下のようになる。

	予測では「良性(0)」	予測では「悪性(1)」
実際は「良性(0)」	89	1
実際は「悪性(1)」	3	50

本当に混同行列指標通りの予測結果となっているかを調べてみよう。
実際の診断結果とロジスティック回帰分析の予測結果をそれぞれy_true、y_predとし、__pandas__の__DataFrame__にcon_max_dfとして格納、それぞれの個数を調べてみた。

con_max_df = pd.DataFrame({
  'y_true': y_test,
  'y_pred': logistic.predict(X_test_scaled)
})
con_max_df['y_true+y_pred'] = con_max_df['y_true'] + con_max_df['y_pred']

print("予測と実際が「良性」\n",con_max_df.query('y_true+y_pred==0').count())
print("予測と実際が「悪性」\n",con_max_df.query('y_true+y_pred==2').count())
print("予測と実際がアンマッチ\n",con_max_df.query('y_true+y_pred==1'))

予測結果、実際の結果が__Confusion matrix__通りに評価されていることが確認できた。

4-2-6.　主成分分析にて各次元の寄与率を調べる

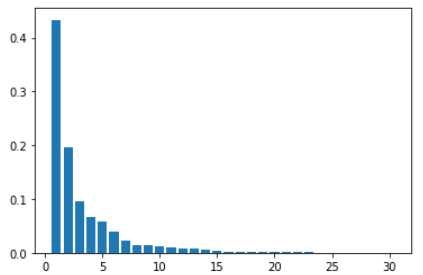
説明変数X_train_scaledで主成分分析を行い、各次元における寄与率を調べ、棒グラフと実際のデータを示す。

pca = PCA(n_components=30)
pca.fit(X_train_scaled)
plt.bar([n for n in range(1, len(pca.explained_variance_ratio_)+1)], pca.explained_variance_ratio_)

寄与率の大きい2次元で63%ほどの寄与率があることから、次元数を2として再度主成分分析を行い、寄与率を調べてみる。

# 次元数2まで圧縮
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)

# 次元圧縮後の次元数
print('X_train_pca shape: {}'.format(X_train_pca.shape))

# 寄与率
print('explained variance ratio: {}'.format(pca.explained_variance_ratio_))

当然であるが、次元数の指定を30として行った主成分分析の上位2次元と指定を2として行った分析の寄与率は同じであることが確認できた。

4-2-7.　主成分分析後のロジスティック回帰分析

次元数2に圧縮した寄与率Total63%の次元データにて、改めてロジスティック回帰分析を行い、次元数30のときの結果と比較してみる。

# 次元数2まで圧縮
pca2 = PCA(n_components=2)
pca3 = PCA(n_components=2)
X_train_pca = pca2.fit_transform(X_train_scaled)
X_test_pca = pca3.fit_transform(X_test_scaled)
print('X_train_pca shape: {}'.format(X_train_pca.shape))
print('X_test_pca shape: {}'.format(X_test_pca.shape))
# 寄与率
print('explained variance ratio: {}'.format(pca2.explained_variance_ratio_))
print('explained variance ratio: {}'.format(pca3.explained_variance_ratio_))

X_train_scaledだけではなくX_test_scaledでの次元数2で主成分分析を行っても、いずれも寄与率63%程度だった。

X_train_scaledを用いてロジスティック回帰分析を行い、前回同様に検証結果を確認してみた。

#主成分分析後の結果を用いて再度ロジスティック回帰分析

# ロジスティック回帰で学習
logistic2 = LogisticRegressionCV(cv=10, random_state=0)
logistic2.fit(X_train_pca, y_train)

# 検証
print('Train score: {:.3f}'.format(logistic2.score(X_train_pca, y_train)))
print('Test score: {:.3f}'.format(logistic2.score(X_test_pca , y_test)))
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic2.predict(X_test_pca))))

• Train score: 98.8%→96.5%
• Test score: 97.2%→91.6%
• Confustion matrix

	予測では「良性(0)」	予測では「悪性(1)」
実際は「良性(0)」	89→83	1→7
実際は「悪性(1)」	3→5	50→48

次元数を圧縮し、寄与率を100%から63%のデータでのロジスティック回帰分析のため、全ての結果が__悪化__している結果となった。しかし、次元数30から次元数2への圧縮により、解析負荷が減っているため、より多くの次元数を伴う解析を行う際は、この__主成分分析__による__次元圧縮__は有効であることが今回の演習でわかった。

5.　アルゴリズム（ｋ近傍法）

5-1.　課題

作成した訓練データを使い、対象データがどのクラスに分類されるかを調べる

5-2.　実装演習

5-2-1.　必要モジュールとデータのインポート

#from モジュール名 import クラス名（もしくは関数名や変数名）
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

読み込むライブラリは、numpy、matplotlib、__scipy__の3つ。__sklearn__は、後ほど読み込むため、ここでは記載していない。

__scipy__はpythonにおける__科学技術計算用__のライブラリである。

5-2-2.　訓練データの作成

def gen_data():
    x0 = np.random.normal(loc=-1, scale=1,size=(25,2)) #平均-1, 標準偏差1, 25行2列のデータ
    x1 = np.random.normal(loc= 1, scale=1,size=(25,2)) #平均 1, 標準偏差1, 25行2列のデータ
    #x0 = np.random.normal(size=50).reshape(-1, 2) - 1
    #x1 = np.random.normal(size=50).reshape(-1, 2) + 1.
    x_train = np.concatenate([x0, x1])
    y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
    return x_train, y_train

X_train, ys_train = gen_data()

今回使用する訓練データを作成する。
平均-1、標準偏差1のデータと平均1、標準偏差1のデータを連結し、50行2列のデータをx_trainとして作成する。また、前半25の要素が0、後半25の要素が1である50行1列のデータをys_trainとして作成する。

#散布図としてプロット
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)

5-2-3.　k近傍法

グラフ描画用にxx0軸100点,xx1軸100点の計10000点の座標データを作成する。

xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

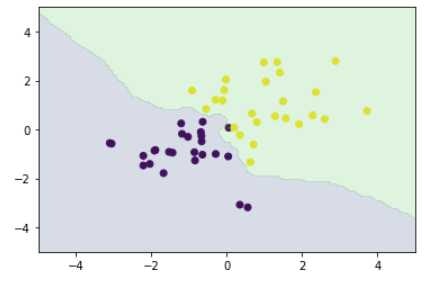
__sklearn__ライブラリの__KNeighborsClassifier__モジュールにて__k近傍法__による分類を行う。そして、10000点のk近傍法による分類データと今回の訓練データを散布図に載せる。

from sklearn.neighbors import KNeighborsClassifier
knc = KNeighborsClassifier(n_neighbors=3).fit(X_train, ys_train)
plt_resut(X_train, ys_train, knc.predict(xx))

また、訓練データにおける予測結果との差異を示す検証結果を示す。

from sklearn.metrics import accuracy_score

y_pred = knc.predict(X_train)
print('Accuracy: %.3f' % accuracy_score(ys_train, y_pred))

今回は98%の検証結果となった。今回は50点の訓練データを使用していたことから、1点のみの差異が出たのみとなっている。

6.　サポートベクターマシン

6-1.　課題

作成した訓練データを使い、対象データ2クラスに分類されるかを調べる

6-2.　実装演習

6-2-1.　必要モジュールとデータのインポート

#from モジュール名 import クラス名（もしくは関数名や変数名）
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

読み込むライブラリは、numpy、__matplotlib__の2つ。__sklearn__は、後ほど読み込むため、ここでは記載していない。

6-2-2.　訓練データの作成

def gen_data():
    x0 = np.random.normal(loc=-1.5, scale=1,size=(25,2)) #平均-1.5, 標準偏差1, 25行2列のデータ
    x1 = np.random.normal(loc= 1.5, scale=1,size=(25,2)) #平均 1.5, 標準偏差1, 25行2列のデータ
    #x0 = np.random.normal(size=50).reshape(-1, 2) - 1.5
    #x1 = np.random.normal(size=50).reshape(-1, 2) + 1.5
    x_train = np.concatenate([x0, x1])
    y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
    return x_train, y_train

X_train, ys_train = gen_data()

今回使用する訓練データを作成する。
平均-1.5、標準偏差1のデータと平均1.5、標準偏差1のデータを連結し、50行2列のデータをx_trainとして作成する。また、前半25の要素が0、後半25の要素が1である50行1列のデータをys_trainとして作成する。

#散布図としてプロット
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)

6-2-3.　サポートベクターマシン

__sklearn__ライブラリの__SVC__モジュールにて__サポートベクターマシン__による分類を行う。

from sklearn.svm import SVC
# 線形SVMのインスタンスを生成
model = SVC(kernel='linear', random_state=None)

# モデルの学習。fit関数で行う。
model.fit(X_train, ys_train)

また、訓練データにおける予測結果との差異を示す検証結果を示す。

from sklearn.metrics import accuracy_score

# トレーニングデータに対する精度
pred_train = model.predict(X_train)
accuracy_train = accuracy_score(ys_train, pred_train)
print('トレーニングデータに対する正解率： %.2f' % accuracy_train)

今回は96%の検証結果となった。今回は50点の訓練データを使用していたことから、2点のみの差異が出たのみとなっている。

from sklearn.metrics import accuracy_score

# トレーニングデータに対する精度
pred_train = model.predict(X_train)
accuracy_train = accuracy_score(ys_train, pred_train)
print('トレーニングデータに対する正解率： %.2f' % accuracy_train)

そして、サポートベクターマシンにより線形分類した結果を散布図に載せると、上記検証結果通り、2点のみ差異が出ている結果となっていることが分かった。

###関連ページ

• ディープラーニング講座「応用数学」要点まとめ
• ディープラーニング講座「機械学習」要点まとめ
• ディープラーニング講座「機械学習」実装演習＜本記事＞
• ディープラーニング講座「深層学習：Day1」要点まとめ＆実装演習
• ディープラーニング講座「深層学習：Day2」要点まとめ＆実装演習
• ディープラーニング講座「深層学習：Day3」要点まとめ＆実装演習
• ディープラーニング講座「深層学習：Day4」要点まとめ＆実装演習