CPLEXによるworkforce scheduling problemの実装・解説

最適化問題の一つである、Workforce Scheduling PropblemをIBM CPLEX上で動かし、その問題の意味や実装の解説を行っていきます。
本問題はIBM ILOG CPLEX上で
ファイル→新規→サンプル→IBM ILOG OPLの例→Task schedulingから参照できます。
（\IBM\ILOG\CPLEX_Studio2211\opl\examples\opl\models\sched_tasks）

本記事で取り上げる問題の説明

Workforce Scheduling Propblem（要員スケジューリング問題）は、期限が設定された依頼に対して遅延を最小限にするように要員をスケジューリングする問題です。
今回は回線の設置の依頼を例にしています。

それぞれの依頼に対し、必要な工事のレシピ(task)とそれを完了するために必要な日数、人員などが定義されています。
また、使用可能な人員が別で定義されています。
それらを用いて遅延を最小限にするように要員をスケジューリングする問題となります。

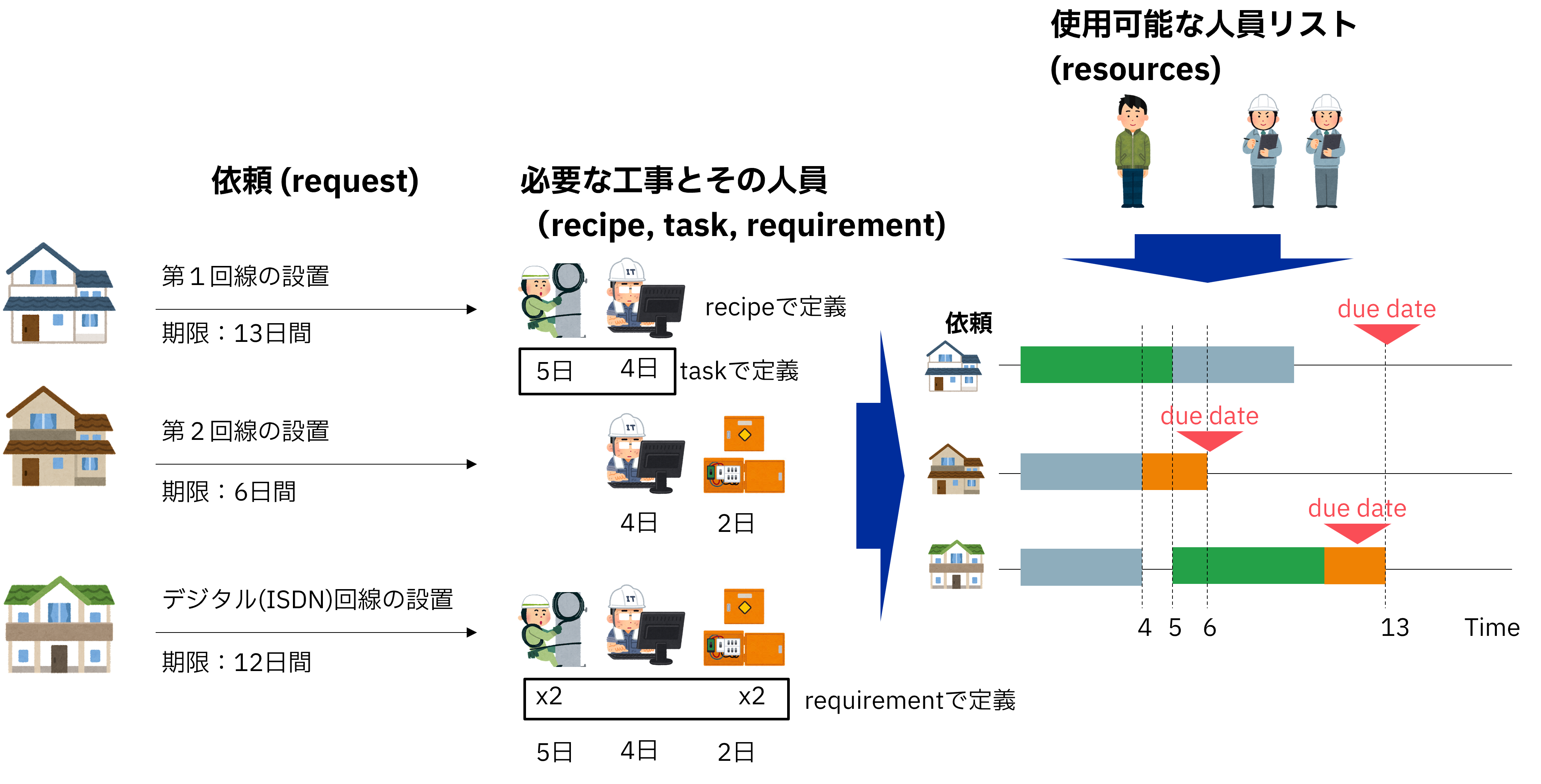
（そのほかの制約として、工事レシピ(task)実施における順序の制約なども存在）

問題設定

下記の例では4つの依頼（id=0~4）が存在し、それぞれの期限（Due Date）が設定されています。それぞれの依頼タイプ（回線種類）に対し、必要な工事レシピ(task)が定義されています。例えば、FirstLineInstallのtypeの場合、FlipSwitchとTestLineの工事メニューを行う必要があります。それぞれの工事レシピ(task)には工数（Processing Time）や順序、必要な人員タイプ（Technician, Operator, etc.)や人員数が定義されています。

データ

上記の問題設定を踏まえた事前に与えられたデータは以下のようになります。

request(依頼）	recipes(依頼完了に必要なtask)	task(taskの工数)

requirement(taskごとに必要な人員）	resources(人員のリソース)	dependencies(タスクの依存関係、task b➡task a)

決定変数

決定変数は、taskの開始時期、終了時期とそれに伴い利用する人員の組み合わせです。

最終的なOutputとしては、以下のような遅延を最小限にするタスクと人員が明記された最適なガントチャートとなります。
ブロック一つがそれぞれの工事task（TestLine, FlipSwitch, ...）となります。

目的変数

遅延を最小化することが目的です。したがって、以下のような式が目的関数となります。

minimize \sum_{i\in tasks} max(0, 完了日_{i}-期限日_{i})

制約

• taskがすべて終わらないとrequestは終わったことにはならない
• taskの完了には、requirementsで定義された(task, resource)ごとのquantity(必要人数)を必要とする。
• taskは事前に定義した順序制約を満たす必要がある。
• 与えられたresource（人員）を使ってtaskを実施する必要がある。
• タスクごとのsize（長さ）が工数（Processing Time）を超えない必要がある。

IBM ILOG CPLEX上での実装、解説

CPLEXの導入

IBM ILOG CPLEXの導入に関してはCPLEXのインストール on Windowsや【学生版】CPLEXのインストール手順に関する情報があまりなかったので書いてみた、また、公式の情報を参考にしてください。

実行方法

• 本問題はIBM ILOG CPLEX上でファイル→新規→サンプル→IBM ILOG OPLの例→Task schedulingから参照できます。
  （\IBM\ILOG\CPLEX_Studio2211\opl\examples\opl\models\sched_tasks）

• インポートしたプロジェクトを右クリック→実行→デフォルトの実行構成から実行できます。

OPLコードの解説

以下2つのファイル（主にmodファイル）について解説していきます。

• sched_tasks.mod:モデルが定義されたモデルファイルです。
• sched_tasks.dat:データが定義されたデータファイルです。

1. データの定義

まずは以下のように必要なデータをデータ構造の形で定義していきます。
OPL言語ではデータ構造をtupleを使って表現します。
C言語のstructと同様です。
詳細はタプルの宣言を参照。

# ResourceDat(人員のリソースデータ)は`id`, `type`, `name`を持つ。
tuple ResourceDat {
  key int id;
  string  type;
  string name;
};

# 回線工事の依頼データ。
# typeはFirstLineInstall, ISDNInstallなどの工事名
# nameは省略名が格納されている（FLIL1など）
tuple RequestDat {
  key int id;
  string  type;
  int     duedate;
  string  name;
};

# 工事ごとに必要なタスク
tuple TaskDat {
  key int id;
  string  type;
  int     ptime;
  string  name;
};

tuple Recipe {
  string request;
  string task;
};

# 順序の定義
tuple Dependency {
  string request;
  string taskb;
  string taska;
  int    delay;
};

# タスクに対する必要な職種と人員の定義
tuple Requirement {
  string task;
  string resource;
  int    quantity;
};

2. データの初期化

下記コードは、定義したタプルの初期化を行っています。詳しくはタプルの初期化を参照してください。
1で作成した構造体の型を持った変数を用意し、datファイルで定義したタプルを使って初期化しています。
ちなみに、OPLは内部と外部での初期化の2通り方法がありますが、今回はdatファイルを用いた外部の初期化となります。詳細は内部および外部の初期化を参照。

# datファイルのデータを格納する。（多分datファイル上の変数名は同じにしないといけない。）
{RequestDat}  requests  = ...;
{ResourceDat} resources = ...;
{TaskDat}     tasks     = ...;
{Recipe}      recipes      = ...;
{Dependency}  dependencies = ...;
{Requirement} requirements = ...;

上記...は省略符号構文と言われ、タプル集合をコンパクトな方法で指定するための構文のようです。

3. タプルデータからのデータ抽出

以下では、datファイルで定義したresourcesの値をsetで保持しています。
具体的には{Operator,Technician,CherryPicker,ISDNPacketMonitor,ISDNTechnician}のように人員の職種が重複なしで入ります。

{string} resourceTypes = { r.type | r in resources };

上記式に関して詳しくはジェネリック集合を参照してください。

4. その他の変数の定義

• Operationはrequest（RequestDat型）と、task（TaskDat型）のタプルになります（タプルのタプル）。

// Set of operations (tasks of a request) and allocations 
// (operation on a possible resource)

tuple Operation {
  RequestDat request;
  TaskDat    task;
};

• Allocationは今まで定義したデータをまとめたデータ構造をもちます。上記で定義したOperation（依頼、タスク）に対して、Requirement（必要な人員数）と、resource（割り当てる人員）をまとめてAllocationとして定義します。

tuple Allocation {
  Operation   dmd;
  Requirement req;
  ResourceDat resource;
};

5. その他変数の初期化

下記コードでは、4で宣言したOperationとAllocationの型の変数(operations, allocs)に初期値を代入していきます。

{Operation} operations = 
  { <r, t> | r in requests,  m in recipes, t in tasks : 
   r.type == m.request && t.type == m.task};

{Allocation} allocs = 
  { <o, m, r> | o in operations, m in requirements, r in resources : 
   o.task.type == m.task && r.type == m.resource};

operationsのコードは、recipesを中間テーブルとして、requestsにtasksを結合しています。(下図)

allocsは、requirementsを中間テーブルとして、operationsとresourcesを結合しています。(下図)

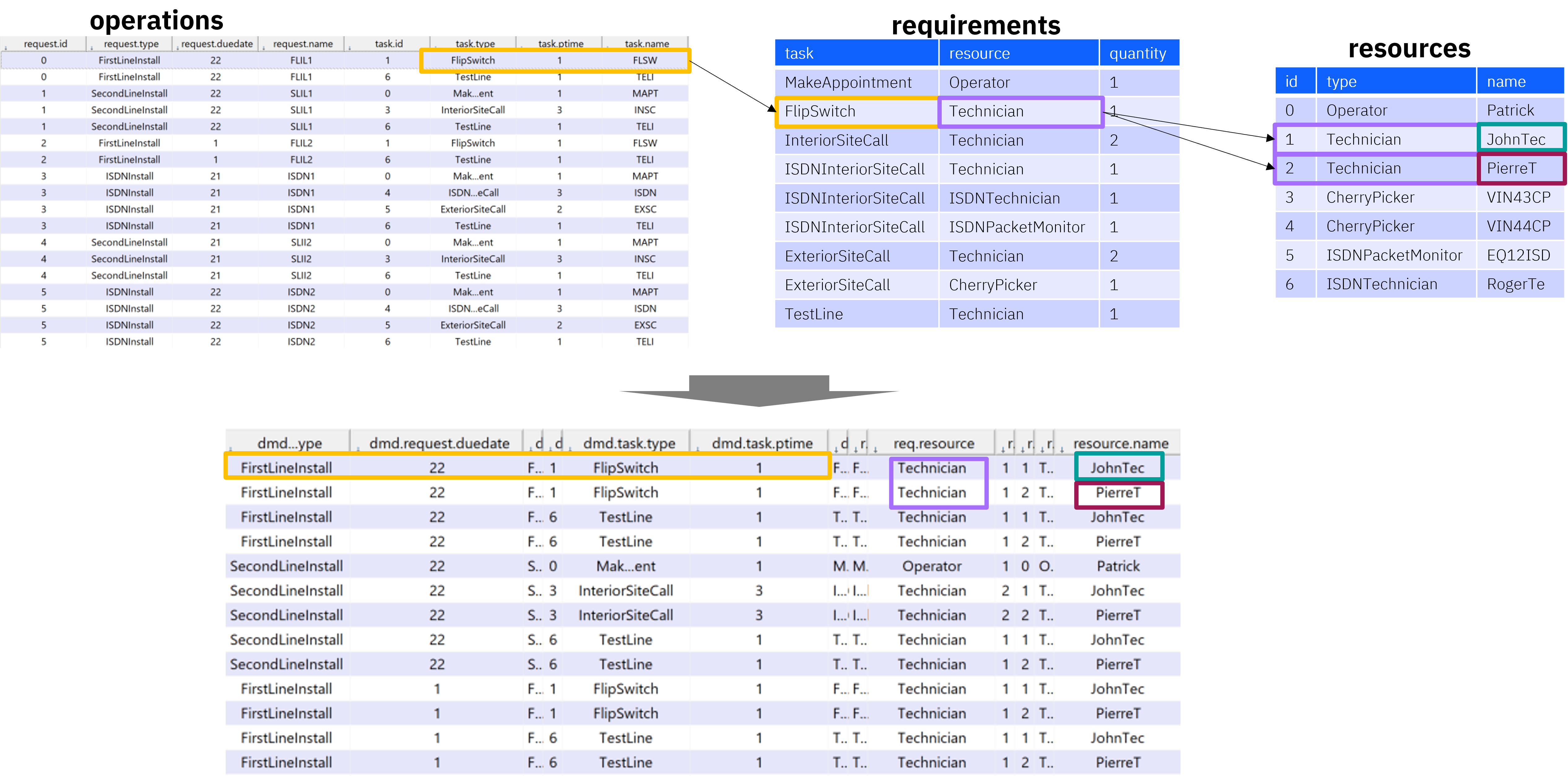
これで、allocs変数には、requestsをもとにrecipe情報とtask情報、requirements情報、resources情報が付与されました。正規化されたテーブルをひとつに結合し、すべての（request, task）に対するresource(人員)の組み合わせを作った、と取れると思います。

ちなみに、上記operationsのコードをPythonで書き換えると以下のようになります

operations = [(r, t) for r in requests for m in recipes for t in tasks if r.type == m.request and t.type == m.task]

6. 決定変数の定義

続いて決定変数を定義します。
dvarは決定変数に使用する OPL キーワードです。
intervalは間隔変数の OPL キーワード (CP、スケジューリング)です。

間隔変数は何かが発生し (例えば、タスクが発生したり、アクティビティーが実行されたりする)、それがいつ発生するかがスケジューリングの問題の不明点であるような時間間隔を表します。間隔は、開始値、終了値、サイズ、および強度によって特徴付けられます。間隔の長さは、その終了時刻から開始時刻を減算したものです。

決定変数を定義するコードは以下で書かれています。

dvar interval tirequests[requests];
dvar interval tiops[o in operations] size o.task.ptime;
dvar interval tiallocs[allocs] optional;

dvar sequence workers[r in resources] in all(a in allocs: a.resource == r) tiallocs[a];

上記で表される配列tirequests[requests]の部分は以下で説明されている通り、タプルの有限集合で添え字をつけています。

決定変数の配列は、データの配列と同じ添字集合を使用して構成できます。特に、有限集合によって決定変数の配列に添字を付けることも可能であり、大きな問題に適しています。以下のコード (抜粋) は、タプルの有限集合 routes で添字が付けられる決定変数の配列 transp を宣言しています。例えば以下のコード (抜粋) があるとします。dvar-例

tuple Route {
string orig;
string dest;
};
{Route} routes = { <"Paris","Roma"> , <"Madrid","Berlin">};
dvar int transp[routes] in 0..100;

tirequests

dvar interval tirequests[requests];

それぞれのrequestに対し、工事を実施する開始日と終了日、長さを決定するための変数です。requestごとにdeadlineが設定されているのでそこを判定するのに使う変数です。
上記で説明した通り、requestsのタプルを決定変数の添え字としています。
求解した後のtirequestsは問題ブラウザーから以下のように表されていることが分かります。

tiops

dvar interval tiops[o in operations] size o.task.ptime;

(request, task)ごとの工事を実施する開始日と終了日、長さを決定するための変数です。
size o.task.ptimeは、タスクごとのsize（長さ）が工数（Processing Time）を超えない制約になります。
求解した後のtiopsは問題ブラウザーから以下のように表されていることが分かります。

tiallocs

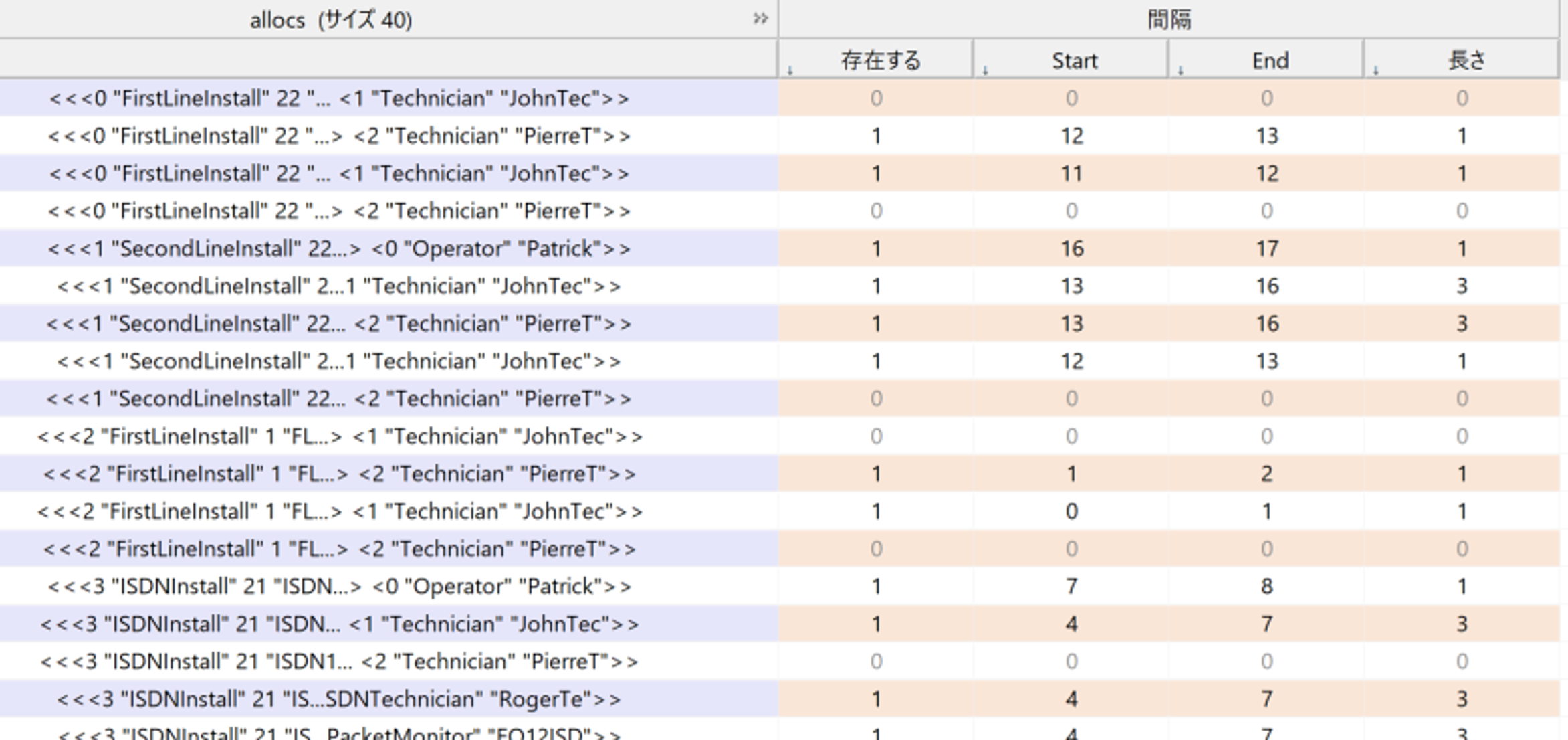
dvar interval tiallocs[allocs] optional;

すべての（request, task）に対するresource(人員)の組み合わせに対して、実際に使用したかしていないか（存在するが1or0）、使用した場合、どの時間からどの時間までどれくらい使用したか、を表すものです。この決定変数が最終的に求めたい変数となり、これをもとにガントチャートを書くことができます。

optionalに関しては以下のような説明がされています。

間隔変数のその他の重要な特徴は、optionalにできることです。つまり、それらを解スケジュールで考慮しないようにできます。
interval

workers

dvar sequence workers[r in resources] in all(a in allocs: a.resource == r) tiallocs[a];

sequenceは、間隔変数のシーケンスを定義するための OPL キーワード (CP、スケジューリング)です。
この決定変数は与えられたresource(人員）が重複して使用されないように制約を設けるときに使用されます。

順序変数は、一連の間隔変数の全体の順序を表します。一連の間隔変数 { a1, a2, a3, a4 } 全体でシーケンス seq が定義されている場合、解でのこのシーケンスの値は (a1, a4, a2, a3) になります。シーケンス内の各間隔変数には、負でない整数 (型) を関連付けることができます。この整数は、シーケンスに対するいくつかの制約によって使用されます (noOverlap を参照)。基本的に、順序変数に対する制約の観点から、同じ型の間隔は、同じ共通の特性を共有します。 順序付けでは、存在しない間隔変数は考慮されないので注意してください。sequence

構文：
dvar sequence p in A [types T];
ここで、
dvar interval A[];
int T[];

workersの定義のコードを直訳すると、all(a in allocs: a.resource == r) tiallocs[a]の部分はallocsの行のうち、resourcesの行と一致するidに対するtiallocsに対して、resourcesのidに対するシーケンスworkersを定めています。

7. 目的関数の定義

minimize sum(t in requests) maxl(0, endOf(tirequests[t]) - t.duedate);

これは目的関数で書いた式をOPL言語で表記したものです。

minimize \sum_{i\in tasks} max(0, 完了日_{i}-期限日_{i})

maxlは最大値を返すOPL関数です。(maxl参照)

8. 制約の定義

subject to {
  forall(r in requests) {
    span(tirequests[r], all(o in operations : o.request == r) tiops[o]);
    forall (o in operations : o.request == r) {
      forall (rc in requirements : rc.task == o.task.type) {
        alternative(tiops[o], all(a in allocs : a.req == rc && a.dmd == o) tiallocs[a], rc.quantity);
      }        
      forall(tc in dependencies: tc.request == r.type && tc.taskb == o.task.type) {
        forall(o2 in operations : o2.request == r && tc.taska == o2.task.type) {
          endBeforeStart(tiops[o], tiops[o2], tc.delay);    
        }
      }
    }   
  }
  forall(r in resources) {
    noOverlap(workers[r]);
  }    
  forall(r in resourceTypes: levels[r] > 1) {
    cumuls[r] <= levels[r];
  }    
};

ひとつづつ見ていきます。

span

  forall(r in requests) {
    span(tirequests[r], all(o in operations : o.request == r) tiops[o]);

まず、spanは以下のような説明がされています。

制約 span(a, {b1, .., bn}) は、間隔 a (存在する場合) が、セット {b1, .., bn} 内の存在するすべての間隔全体にわたってスパンしていることを示します。つまり、間隔 a は、{b1, .., bn} 内の存在する最初の間隔と一緒に開始され、存在する最後の間隔と一緒に終了します。aが存在しない場合、b 間隔は存在しません。

つまり、求めたrequestの間隔が存在するtaskのすべての間隔全体にわたってスパンしていること、となります。これは以下の図で言うと、赤の矢印は緑の矢印の開始地点から紫の矢印の終了地点までスパンしているということになります。taskがすべて終わらないとrequestは終わったことにはならないという制約です。

alternative

forall (o in operations : o.request == r) {
      forall (rc in requirements : rc.task == o.task.type) {
        alternative(tiops[o], all(a in allocs : a.req == rc && a.dmd == o) tiallocs[a], rc.quantity);
      }

alternativeは、以下のような説明がされています。

制約 alternative(a, {b1, .., bn},c) では、セット {b1, .., bn} での c 個の間隔の選択がモデル化されます。間隔 a が存在する場合は、{b1, .., bn} に c 個の間隔が存在し、その選択された間隔とともに a が開始し、終了します。a が存在しない場合は、すべての b 間隔が存在しません。一般にこの制約は、一連の候補リソースからの 1 つのリソース (または c 個のリソース) の選択をモデル化するために使用されます。また、より複雑なケースでアクティビティーの代替実行モードやタスクを実行するための代替時間ウィンドウをモデル化する場合にも使用できます。

今回の制約は、requirementsで定義された(task, resource)ごとのquantity(必要人数)を指定しています。

endBeforeStart

      forall(tc in dependencies: tc.request == r.type && tc.taskb == o.task.type) {
        forall(o2 in operations : o2.request == r && tc.taska == o2.task.type) {
          endBeforeStart(tiops[o], tiops[o2], tc.delay);   

endBeforeStartは以下のような説明がなされています。

この制約は、(オプションの時間値 z によって変更された) 特定の間隔変数 a の終了が、特定の間隔変数 b の開始以下である (e(a) + z ≤ s(b)) ことを示します。

これはdatファイルで定義したdependenciesの順序制約を満たすような式になります。

noOverlap

  forall(r in resources) {
    noOverlap(workers[r]);
  }

noOverlapは以下のような説明がなされています。

間隔順序変数 p に対する noOverlap 制約は、シーケンスが、オーバーラップしない間隔のチェーンを定義することを示します。ここで、チェーン内の間隔は、チェーン内の次の間隔が開始される前に終了するように制約されます。通常、この制約は、離接リソースのモデル化に役立ちます。

これは以下で表されるresourcesが同時刻で使用されない（重複しない）制約となります。

9. 決定式（cumul）

cumulFunction cumuls[rt in resourceTypes] =
  sum(rc in requirements, o in operations : rc.resource == rt && o.task.type == rc.task) pulse(tiops[o], rc.quantity);

subject to {
...
  forall(r in resourceTypes: levels[r] > 1) {
    cumuls[r] <= levels[r];
  }    
};

To be updated

結果

結果は下記のようにガントチャートで表現することができます。
下記はtiallocsの結果。

また、決定式を使うと、下図のように誰がどの時間にアサインされたかを見ることができます。

コード全体

using CP;

// Data for resources, requests and tasks

tuple ResourceDat {
  key int id;
  string  type;
  string name;
};

tuple RequestDat {
  key int id;
  string  type;
  int     duedate;
  string  name;
};

tuple TaskDat {
  key int id;
  string  type;
  int     ptime;
  string  name;
};

{RequestDat}  requests  = ...;
{ResourceDat} resources = ...;
{TaskDat}     tasks     = ...;

{string} resourceTypes = { r.type | r in resources };

// Data for template recipes, dependencies and requirements

tuple Recipe {
  string request;
  string task;
};

tuple Dependency {
  string request;
  string taskb;
  string taska;
  int    delay;
};

tuple Requirement {
  string task;
  string resource;
  int    quantity;
};

{Recipe}      recipes      = ...;
{Dependency}  dependencies = ...;
{Requirement} requirements = ...;

// Set of operations (tasks of a request) and allocations (operation on a possible resource)

tuple Operation {
  RequestDat request;
  TaskDat    task;
};

tuple Allocation {
  Operation   dmd;
  Requirement req;
  ResourceDat resource;
};

{Operation} operations = 
  { <r, t> | r in requests,  m in recipes, t in tasks : 
   r.type == m.request && t.type == m.task};

{Allocation} allocs = 
  { <o, m, r> | o in operations, m in requirements, r in resources : 
   o.task.type == m.task && r.type == m.resource};

dvar interval tirequests[requests];
dvar interval tiops[o in operations] size o.task.ptime;
dvar interval tiallocs[allocs] optional;

dvar sequence workers[r in resources] in all(a in allocs: a.resource == r) tiallocs[a];

int levels[rt in resourceTypes] = sum(r in resources : r.type == rt) 1;

cumulFunction cumuls[rt in resourceTypes] =
  sum(rc in requirements, o in operations : rc.resource == rt && o.task.type == rc.task) pulse(tiops[o], rc.quantity);

minimize sum(t in requests) maxl(0, endOf(tirequests[t]) - t.duedate);
subject to {
  forall(r in requests) {
    span(tirequests[r], all(o in operations : o.request == r) tiops[o]);
    forall (o in operations : o.request == r) {
      forall (rc in requirements : rc.task == o.task.type) {
        alternative(tiops[o], all(a in allocs : a.req == rc && a.dmd == o) tiallocs[a], rc.quantity);
      }        
      forall(tc in dependencies: tc.request == r.type && tc.taskb == o.task.type) {
        forall(o2 in operations : o2.request == r && tc.taska == o2.task.type) {
          endBeforeStart(tiops[o], tiops[o2], tc.delay);    
        }
      }
    }   
  }
  forall(r in resources) {
    noOverlap(workers[r]);
  }    
  forall(r in resourceTypes: levels[r] > 1) {
    cumuls[r] <= levels[r];
  }    
};