$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
はじめに
加算、剰余加算、制御-剰余乗算という具合に見てきましたが、それは「Shorのアルゴリズム」で重要な役割を果たす「べき剰余」を実行するための準備として、という位置づけでした。今回はその「べき剰余」について見ていきます。アルゴリズムを説明した後、自作の量子計算シミュレータqlazyで、動作を確認します。
参考にさせていただいた論文は以下です。
べき剰余の実現方法
参考論文に全体の回路図が出ているので、まずそれを掲載します。
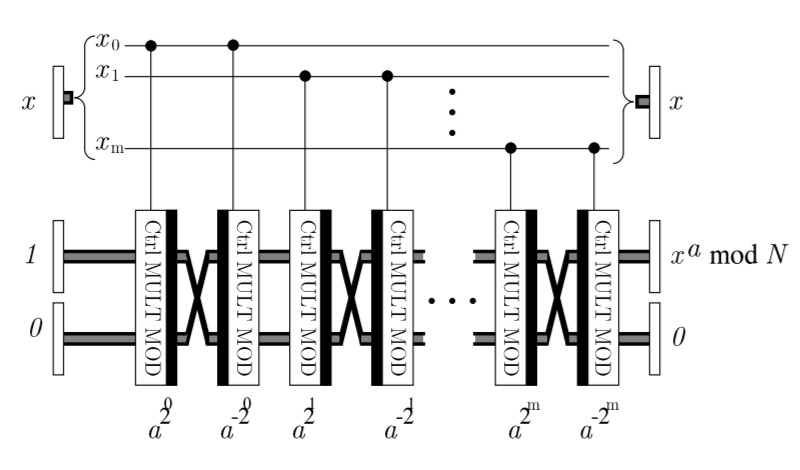
$a^x \space mod \space N$という「べき剰余」を実行する回路です(図には$x^a \space mod \space N$と書いてありますが、$a^x \space mod \space N$の間違いではないかと思われます)。
図を見てわかる通り、前回の記事で確認した「制御-剰余乗算(以下CMMと省略)」とスワップ(以下SWAPと表記)とCMMの逆演算(以下iCMMと表記)をセットにして繰り返し適用していくだけなので、考え方はそれほど難しくないです。
説明のため、レジスタに名前をつけます。図の左側の上にxと記載してあるレジスタを<x>、1と記載してあり最終結果が格納されるレジスタを<xx>、一番下の0と記載されている レジスタを<y>と名付けておきます。aを格納するレジスタが記載されていないですが、この量子計算を実現するために外から与えるパラメータのようなもので、あえて言うなら古典レジスタに格納されていると思えば良いと思います。その他、CMMを実現するために必要になるレジスタもありますが、詳細は前回の記事を参照してください。
では、左から順に、レジスタ<xx>とレジスタ<y>の状態変化を表にして示します。状態なのでケット記号を使って$\ket{A}$のように記載すべきなのですが、簡単のため$A$とのみ記載します。また、各段階での計算は$mod \space N$前提で実行しているものと思ってください。xの値によって、各段階のCMMやSWAPやiCMMがONになったりOFFになったりするので、場合分けをして表にしてみました。
- $x=0$ ($x_{0}=0,x_{1}=0$)の場合
| レジスタ | 初期状態 | 0番目のCMM | SWAP | 0番目のiCMM | 1番目のCMM | SWAP | 1番目のiCMM |
|---|---|---|---|---|---|---|---|
| <xx> | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ |
| <y> | $0$ | $0$ | $0$ | $0$ | $0$ | $0$ | $0$ |
- $x=1$ ($x_{0}=1,x_{1}=0$)の場合
| レジスタ | 初期状態 | 0番目のCMM | SWAP | 0番目のiCMM | 1番目のCMM | SWAP | 1番目のiCMM |
|---|---|---|---|---|---|---|---|
| <xx> | $1$ | $a$ | $1$ | $a$ | $a$ | $a$ | $a$ |
| <y> | $0$ | $1$ | $a$ | $0$ | $0$ | $0$ | $0$ |
- $x=2$ ($x_{0}=0,x_{1}=1$)の場合
| レジスタ | 初期状態 | 0番目のCMM | SWAP | 0番目のiCMM | 1番目のCMM | SWAP | 1番目のiCMM |
|---|---|---|---|---|---|---|---|
| <xx> | $1$ | $1$ | $1$ | $1$ | $1$ | $a^{2}$ | $a^{2}$ |
| <y> | $0$ | $0$ | $0$ | $0$ | $a^{2}$ | $1$ | $0$ |
- $x=3$ ($x_{0}=1,x_{1}=1$)の場合
| レジスタ | 初期状態 | 0番目のCMM | SWAP | 0番目のiCMM | 1番目のCMM | SWAP | 1番目のiCMM |
|---|---|---|---|---|---|---|---|
| <xx> | $1$ | $a$ | $1$ | $a$ | $a$ | $a^{3}$ | $a^{3}$ |
| <y> | $0$ | $1$ | $a$ | $0$ | $a^{3}$ | $a$ | $0$ |
というわけで、レジスタ<xx>に$a^{x} \space mod \space N$の値が入ることがわかります。ここで1点注意しておきたいのがSWAPの動作です。回路図のSWAPには制御ビットとつながる線が書かれていませんが、CMM-SWAP-iCMMが一体となって制御ビットとつながっていることを意味しています。つまり、SWAPは厳密に言うと、制御SWAP(正式名称は知りません。フレドキンゲートの拡張みたいですがちょっと違うかな?)です。
さて、"CMM-SWAP-iCMM"のセットを2回繰り返したところまで書けたので、あとはこれを延長すれば、任意のべき剰余が計算できるというわけです。
数式で説明すると、以下のような量子計算を$i=0,1,2,...$と繰り返していると思えば良いです。
\begin{align}
& \ket{a^{2^0 x_0 + 2^1 x_1 + \cdots 2^{i-1} x_{i-1}}, 0} \\
& \rightarrow \ket{a^{2^0 x_0 + 2^1 x_1 + \cdots 2^{i-1} x_{i-1}},a^{2^0 x_0 + 2^1 x_1 + \cdots 2^{i} x_{i}}} \\
& \rightarrow \ket{a^{2^0 x_0 + 2^1 x_1 + \cdots 2^{i} x_{i}},a^{2^0 x_0 + 2^1 x_1 + \cdots 2^{i-1} x_{i-1}}} \\
& \rightarrow \ket{a^{2^0 x_0 + 2^1 x_1 + \cdots 2^{i} x_{i}}, 0}
\end{align}
ここで、1行目から2行目はCMM、2行目から3行目はSWAP、3行目から4行目はiCMMの演算を表しています。これを$n$回繰り返すと、最大で$x=2^{n}-1$までのべき剰余$a^{x} \space mode \space N$が実行できることがわかります。
シミュレータで動作確認
それでは、シミュレータで動作確認をしていくのですが、その前に各レジスタに必要となるビット数を見積もってみます。上の図だけ見ると、とてもシンプルに見えるのですが、CMMやiCMMを実現するためには内部で「剰余加算」を実行していて、「剰余加算」を実行するために内部で「加算」を実行していて、各々を実行するために多くの補助レジスタが必要になります。シミュレータでの実行は限定されたメモリ範囲内でやるしかないため、今回はとても小さい数での動作確認になります。具体的には、$a=2,N=3,x=0,1,2$で動作させることを前提にします。
まず、$a=2$については外部パラメータということで量子レジスタとして割り当てることはしません。$x$については2ビットで十分なので、レジスタ<x>には2ビットを割り当てます。レジスタ<xx>には、$mod \space 3$の結果が格納されるので2ビット割り当てることにします。CMMを実行するために、内部で剰余加算を実行しますが、それへの入力レジスタが別途必要になり、今回レジスタ<xxx>と名付けることにします(前回の制御-剰余乗算の記事では<xx>と呼んでいました)。<xxx>には最大で$a^2=4$が入るので、3ビット割り当てます。<y>は、CMMの内部で剰余加算をするもう一方の入力レジスタなので、<xxx>よりも1つ多いビット数を用意しておく必要があるため、4ビットとします。加算を実行するためには桁上げ情報格納のためのレジスタ<c>がさらに必要になります。それには<y>と同じ数のビットを用意しておき、最上位の1ビットを<y>と共有するため、追加で3ビット必要になります。$N=3$を格納するためのレジスタも、上の回路図には書かれていないですが、必要です。剰余加算回路の内部で<xxx>とスワップするため同じビット数、すなわち3ビットを割り当てます。その他、剰余加算でアンダーフロー記述のための補助レジスタが1ビット必要になります。以上、すべてを合わせると「18量子ビット」となります。ちょっとややこしい説明になってしまいましたが、前回までの、加算、剰余加算、制御-剰余乗算の記事をよく見ればわかると思います(と言いつつ、間違っていたらすみません、汗)。
それではシミュレータで、「べき剰余」の動作を確認してみます。先程説明したように、$a=2,N=3,x=0,1,2$で動作させます。x=3の場合は、今回ビット数の関係で諦めましたので、xのすべての値に対して重ね合わせることはせず、$x=0,1,2$でforループを回して結果を逐一表示するようにしました。全体のPythonコードは以下の通りです。
【2021.9.5追記】qlazy最新版でのソースコードはここに置いてあります。
from qlazypy import QState
def swap(self,id_0,id_1):
Arithmetic/ctr_modular_multiplier_1.py
dim = min(len(id_0),len(id_1))
for i in range(dim):
self.cx(id_0[i],id_1[i]).cx(id_1[i],id_0[i]).cx(id_0[i],id_1[i])
return self
def ctr_swap(self,id_ctr,id_0,id_1):
dim = min(len(id_0),len(id_1))
for i in range(dim):
self.ccx(id_ctr[0],id_0[i],id_1[i])
self.ccx(id_ctr[0],id_1[i],id_0[i])
self.ccx(id_ctr[0],id_0[i],id_1[i])
return self
def sum(self,q0,q1,q2):
self.cx(q1,q2).cx(q0,q2)
return self
def i_sum(self,q0,q1,q2):
self.cx(q0,q2).cx(q1,q2)
return self
def carry(self,q0,q1,q2,q3):
self.ccx(q1,q2,q3).cx(q1,q2).ccx(q0,q2,q3)
return self
def i_carry(self,q0,q1,q2,q3):
self.ccx(q0,q2,q3).cx(q1,q2).ccx(q1,q2,q3)
return self
def plain_adder(self,id_a,id_b,id_c):
depth = len(id_a)
for i in range(depth):
self.carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.cx(id_a[depth-1],id_b[depth-1])
self.sum(id_c[depth-1],id_a[depth-1],id_b[depth-1])
for i in reversed(range(depth-1)):
self.i_carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.sum(id_c[i],id_a[i],id_b[i])
return self
def arrow(self,N,q,id):
for i in range(len(id)):
if (N>>i)%2 == 1:
self.cx(q,id[i])
return self
def arrow2(self,i,a,id_ctr,id_x,id_xx):
aa = a * 2**i
for j in range(len(id_xx)):
if (aa>>j)%2 == 1:
self.ccx(id_ctr[0],id_x[i],id_xx[j])
return self
def arrow3(self,id_ctr,id_x,id_y):
for j in range(len(id_x)):
self.ccx(id_ctr[0],id_x[j],id_y[j])
return self
def i_plain_adder(self,id_a,id_b,id_c):
depth = len(id_a)
for i in range(depth-1):
self.i_sum(id_c[i],id_a[i],id_b[i])
self.carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.i_sum(id_c[depth-1],id_a[depth-1],id_b[depth-1])
self.cx(id_a[depth-1],id_b[depth-1])
for i in reversed(range(depth)):
self.i_carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
return self
def modular_adder(self,N,id_a,id_b,id_c,id_N,id_t):
self.plain_adder(id_a,id_b,id_c)
self.swap(id_a,id_N)
self.i_plain_adder(id_a,id_b,id_c)
self.x(id_b[len(id_b)-1])
self.cx(id_b[len(id_b)-1],id_t[0])
self.x(id_b[len(id_b)-1])
self.arrow(N,id_t[0],id_a)
self.plain_adder(id_a,id_b,id_c)
self.arrow(N,id_t[0],id_a)
self.swap(id_a,id_N)
self.i_plain_adder(id_a,id_b,id_c)
self.cx(id_b[len(id_b)-1],id_t[0])
self.plain_adder(id_a,id_b,id_c)
return self
def i_modular_adder(self,N,id_a,id_b,id_c,id_N,id_t):
self.i_plain_adder(id_a,id_b,id_c)
self.cx(id_b[len(id_b)-1],id_t[0])
self.plain_adder(id_a,id_b,id_c)
self.swap(id_a,id_N)
self.arrow(N,id_t[0],id_a)
self.i_plain_adder(id_a,id_b,id_c)
self.arrow(N,id_t[0],id_a)
self.x(id_b[len(id_b)-1])
self.cx(id_b[len(id_b)-1],id_t[0])
self.x(id_b[len(id_b)-1])
self.plain_adder(id_a,id_b,id_c)
self.swap(id_a,id_N)
self.i_plain_adder(id_a,id_b,id_c)
return self
def ctr_modular_multiplier(self,a,N,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t):
depth = len(id_x)
for i in range(depth):
self.arrow2(i,a,id_ctr,id_x,id_xx)
self.modular_adder(N,id_xx,id_y,id_c,id_N,id_t)
self.arrow2(i,a,id_ctr,id_x,id_xx)
self.x(id_ctr[0])
self.arrow3(id_ctr,id_x,id_y)
self.x(id_ctr[0])
return self
def i_ctr_modular_multiplier(self,a,N,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t):
depth = len(id_x)
self.x(id_ctr[0])
self.arrow3(id_ctr,id_x,id_y)
self.x(id_ctr[0])
for i in reversed(range(depth)):
self.arrow2(i,a,id_ctr,id_x,id_xx)
self.i_modular_adder(N,id_xx,id_y,id_c,id_N,id_t)
self.arrow2(i,a,id_ctr,id_x,id_xx)
return self
def modular_exponentiation(self,a,N,id_x,id_xx,id_xxx,id_y,id_c,id_N,id_t):
depth = len(id_x)
id_ctr = [0]
for i in range(depth):
aa = a**(2**i)
id_ctr[0] = id_x[i]
self.ctr_modular_multiplier(aa,N,id_ctr,id_xx,id_xxx,id_y,id_c,id_N,id_t)
self.ctr_swap(id_ctr,id_xx,id_y)
self.i_ctr_modular_multiplier(aa,N,id_ctr,id_xx,id_xxx,id_y,id_c,id_N,id_t)
return self
def encode(self,decimal,id):
for i in range(len(id)):
if (decimal>>i)%2 == 1:
self.x(id[i])
return self
def decode(self,id):
iid = id[::-1]
return self.m(id=iid,shots=1).lst
def create_register():
num = 0
id_x = [i for i in range(2)]
num += len(id_x)
id_xx = [i+num for i in range(2)]
num += len(id_xx)
id_xxx = [i+num for i in range(3)]
num += len(id_xxx)
id_y = [i+num for i in range(4)]
num += len(id_y)
id_c = [i+num for i in range(4)]
id_c[len(id_c)-1] = id_y[len(id_y)-1]
num += (len(id_c)-1)
id_N = [i+num for i in range(3)]
num += len(id_N)
id_t = [i+num for i in range(1)]
num += len(id_t)
id_r = id_xx
return (num,id_x,id_xx,id_xxx,id_y,id_c,id_N,id_t,id_r)
if __name__ == '__main__':
# add methods
QState.swap = swap
QState.ctr_swap = ctr_swap
QState.sum = sum
QState.i_sum = i_sum
QState.carry = carry
QState.i_carry = i_carry
QState.arrow = arrow
QState.arrow2 = arrow2
QState.arrow3 = arrow3
QState.plain_adder = plain_adder
QState.i_plain_adder = i_plain_adder
QState.modular_adder = modular_adder
QState.i_modular_adder = i_modular_adder
QState.ctr_modular_multiplier = ctr_modular_multiplier
QState.i_ctr_modular_multiplier = i_ctr_modular_multiplier
QState.modular_exponentiation = modular_exponentiation
QState.encode = encode
QState.decode = decode
# set input numbers
a = 2
N = 3
x_list = [0,1,2]
# create registers
num,id_x,id_xx,id_xxx,id_y,id_c,id_N,id_t,id_r = create_register()
for x in x_list:
# initialize quantum state
qs = QState(num)
qs.encode(x,id_x)
qs.encode(N,id_N)
qs.encode(1,id_xx)
# execute controlled modular multiplier
qs.modular_exponentiation(a,N,id_x,id_xx,id_xxx,id_y,id_c,id_N,id_t)
res = qs.decode(id_r)
print("{0:}^{1:} mod {2:} -> {3:}".format(a,x,N,res))
qs.free()
前回までの記事(加算、剰余加算、制御-剰余乗算)で、大半の関数は説明済なので、今回の差分だけを説明します。
def ctr_swap(self,id_ctr,id_0,id_1):
dim = min(len(id_0),len(id_1))
for i in range(dim):
self.ccx(id_ctr[0],id_0[i],id_1[i])
self.ccx(id_ctr[0],id_1[i],id_0[i])
self.ccx(id_ctr[0],id_0[i],id_1[i])
return self
で、制御ビットつきのスワップを定義しています。通常のスワップは制御NOTを3つ組み合わせますが、さらに別の制御ビットによってON/OFF制御するため、制御-制御NOT、つまりToffoliゲート3つに置き換えています。
def modular_exponentiation(self,a,N,id_x,id_xx,id_xxx,id_y,id_c,id_N,id_t):
depth = len(id_x)
id_ctr = [0]
for i in range(depth):
aa = a**(2**i)
id_ctr[0] = id_x[i]
self.ctr_modular_multiplier(aa,N,id_ctr,id_xx,id_xxx,id_y,id_c,id_N,id_t)
self.ctr_swap(id_ctr,id_xx,id_y)
self.i_ctr_modular_multiplier(aa,N,id_ctr,id_xx,id_xxx,id_y,id_c,id_N,id_t)
return self
で、べき剰余を定義しています。上で示した回路図をそのまま実行しています。
def create_register():
num = 0
id_x = [i for i in range(2)]
num += len(id_x)
id_xx = [i+num for i in range(2)]
num += len(id_xx)
id_xxx = [i+num for i in range(3)]
num += len(id_xxx)
id_y = [i+num for i in range(4)]
num += len(id_y)
id_c = [i+num for i in range(4)]
id_c[len(id_c)-1] = id_y[len(id_y)-1]
num += (len(id_c)-1)
id_N = [i+num for i in range(3)]
num += len(id_N)
id_t = [i+num for i in range(1)]
num += len(id_t)
id_r = id_xx
return (num,id_x,id_xx,id_xxx,id_y,id_c,id_N,id_t,id_r)
で、各レジスタに割り当てる量子ビット番号と全体の量子ビット数を計算してリターンする関数を定義しています。
というわけで、プログラム本体の説明です。
# set input numbers
a = 2
N = 3
x_list = [0,1,2]
# create registers
num,id_x,id_xx,id_xxx,id_y,id_c,id_N,id_t,id_r = create_register()
$a,N$の値と$x$の値を入れるリストを設定して、各レジスタおよび必要となる全体量子ビット数を適当な変数に格納します。
for x in x_list:
# initialize quantum state
qs = QState(num)
qs.encode(x,id_x)
qs.encode(N,id_N)
qs.encode(1,id_xx)
# execute controlled modular multiplier
qs.modular_exponentiation(a,N,id_x,id_xx,id_xxx,id_y,id_c,id_N,id_t)
res = qs.decode(id_r)
print("{0:}^{1:} mod {2:} -> {3:}".format(a,x,N,res))
xの値を変えながら、べき剰余の計算を実行し、その結果を逐次表示します。
実行結果は、以下の通りです。
2^0 mod 3 -> 1
2^1 mod 3 -> 2
2^2 mod 3 -> 1
というわけで、べき剰余が正しく計算できることが確認できました。
おわりに
結局、とても小さい数でしか実行できませんでしたが、とりあえず確認できたことにします。今回18量子ビットという見積りのもとで実行しましたが、参考論文には$N$のビット数$n$に対して、$7n+1$量子ビットで良いという記載があります。だとすると、本当は15量子ビットで実行可能なはず、ということでしょうか?ちょっとわかりませんが、もしかすると何らかの誤まった解釈から余分な量子ビットを使ってしまっているのかもしれません(が、すみません。今回はここまでとします。みなさま、お使いのシミュレータで実行してみて、量子ビット削減できたよ!ということが、もしあれば、後で教えて下さい)。
「べき剰余」のアルゴリズムについては、今回参考にした論文が発表された1990年代半ば以降、研究の進展がとてもあるようなので、今後余裕があれば見ておこうと思います。
次回は、予定では「Shorのアルゴリズム」なのですが、べき剰余の部分をどうしようか、考え中です。
以上