$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
はじめに
前々回、前回に引き続き、算術演算シリーズです。今回は「制御-剰余乗算(Controlled-multiplier modulo N)」です。アルゴリズムを説明した後、自作の量子計算シミュレータqlazyで、動作の確認をします。
参考にさせていただいた論文は以下です。
制御-剰余乗算の実現方法
参考論文に全体の回路図が出ているので、まずそれを掲載します。
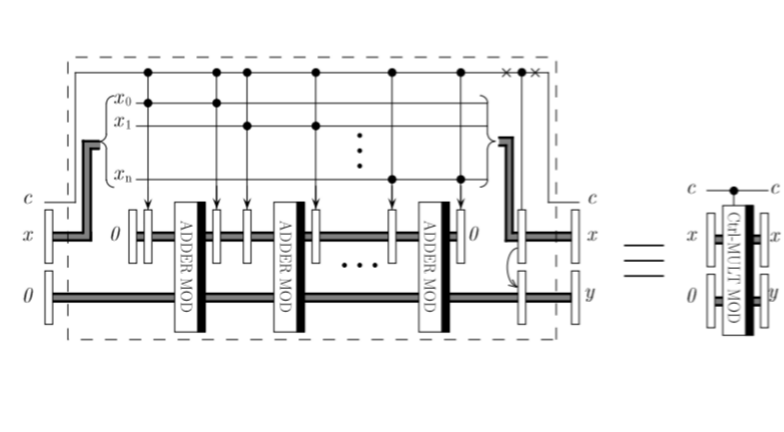
論文には、
\ket{c;x,0} \rightarrow \left\{
\begin{array}{}
\ket{c;x,a \times x \space mod \space N} & if \space \ket{c} = \ket{1} \\
\ket{c;x,x} & if \space \ket{c} = \ket{0}
\end{array}
\right.
という制御-剰余乗算を計算する回路と説明されています。これで本当にその計算が実現できるのか、以下で見ていきます。
まずはじめに必要となるレジスタの確認をします。制御ビット$c$用のレジスタを<ctr>、$x,y(=a \times x \space mod \space N)$用のレジスタを<x>,<y>、剰余加算ADDER MODへの一方の入力で必要になるレジスタ(図でADDER MODに入っている2つのレジスタのうち上の方)を<xx>と呼ぶことにします。また、図には記載されていませんが、ADDER MODを動作させるためのレジスタとして、加算の桁上げ情報格納のためのレジスタ<c>と$N$を入れておくためのレジスタ<N>とアンダーフロー情報格納用の補助レジスタ<t>が必要になります(前々回、前回の記事を参照)。$a$がどこにも登場していませんが、この量子計算を実行するためのパラメータということで明示的には書かれていません(あえて言うなら古典レジスタに格納しておくということでしょうか)。
次に、各レジスタに必要となるビット数を見積もってみます。まず、$a$は$n$ビットの数とし、レジスタ<x>には$n$ビット割り当てるものとします。つまり、$n$ビット同士の制御-剰余乗算を考えます。レジスタ<xx>には、後で説明する通り、最大$2^{n-1}a$という値が入るので$2n-1$ビットとしておきます。ADDER MODのもう一方のレジスタ<y>のビット数はそれよりも1つ大きくしておくので$2n$ビット割り当てます。とすると、図に記載されていない補助レジスタ<c>は$2n-1$ビットとなり、$N$を格納するレジスタ<N>はレジスタ<xx>と等しくしておくので、$2n-1$ビット必要となります。最後にレジスタ<t>と<ctr>ですが、これは各々$1$ビットに決まっています。というわけで、合計すると$9n-1$ビット必要ということになります(参考論文には、こと細かく説明されていないので、自分の解釈に基づき見積もりました。間違っていたらご指摘いただけるとありがたいです。ただ、下でも示すとおり、この前提でシミュレータを動かしたら一応正しい結果は得られました)。
さて、それでは実際の量子計算について見ていきます。$ax$の$x$を2進数に展開すると、
ax = 2^{0} a x_{0} + 2^{1} a x_{1} + \cdots + 2^{i} a x_{i} + \cdots + 2^{n-1} a x_{n-1}
と書くことができますが、これの右辺を第1項から順番に剰余加算していくイメージです。
最初のADDER MODの前に矢印がささったような演算子が書かれています。これは、2つの制御ビットがともに1のときのみ、矢印がささっているレジスタを$2^{i}a$にして、それ以外の場合、何もしない(つまり$0$のままとする)演算子と定義されています(前回の記事で出てきた「アロー演算子」に似ていますが別物です。ここでは区別するため「アロー演算子2」と呼ぶことにします)。最初ののADDER MODの前にかかってるアロー演算子2は、$i=0$の場合なので、レジスタ<ctr>とレジスタ<x>の0番目のビットがともに1の場合のみ、レジスタ<xx>の値は$2^{0} a$となり、それ以外は$0$となります。最初のADDER MODの計算結果は、制御ビットが1の場合、$2^{0} a \space mod \space N$となります。次のアロー演算子2はレジスタ<xx>の値を0に戻すためのものです。以下、$i=1,2,...,n-1$と計算していくことで、レジスタ<y>に剰余加算の結果が積み重なっていき、最終的に$a \times x \space mod \space N$の値が一番右の<y>レジスタに格納されることになります。
最後のレジスタの直前に<x>レジスタと<y>レジスタが矢印でつながっていて、さらに制御ビットから線が伸びているような不思議な演算子が書かれています。これは制御ビットが0の場合に、<y>レジスタを<x>に等しくするためのものです。<x>レジスタの各ビットが1かどうかを見て、1の場合、それに対応したレジスタ<y>のビットを反転させる演算子です(ここでは「アロー演算子3」と呼ぶことにします)。
シミュレータで動作確認
それではシミュレータで、この制御-剰余乗算の動作を確認します。今回想定したのは、2ビット同士の乗算に関する制御-剰余乗算です。具体的には、a=3,N=5を固定にして、xを取りうる値すべて(0,1,2,3,4)の重ね合わせとして、一気に制御-剰余加算をやってみます。全体のPythonコードは以下の通りです。
【2021.9.5追記】qlazy最新版でのソースコードはここに置いてあります。
from qlazypy import QState
def swap(self,id_0,id_1):
dim = min(len(id_0),len(id_1))
for i in range(dim):
self.cx(id_0[i],id_1[i]).cx(id_1[i],id_0[i]).cx(id_0[i],id_1[i])
return self
def sum(self,q0,q1,q2):
self.cx(q1,q2).cx(q0,q2)
return self
def i_sum(self,q0,q1,q2):
self.cx(q0,q2).cx(q1,q2)
return self
def carry(self,q0,q1,q2,q3):
self.ccx(q1,q2,q3).cx(q1,q2).ccx(q0,q2,q3)
return self
def i_carry(self,q0,q1,q2,q3):
self.ccx(q0,q2,q3).cx(q1,q2).ccx(q1,q2,q3)
return self
def plain_adder(self,id_a,id_b,id_c):
depth = len(id_a)
for i in range(depth):
self.carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.cx(id_a[depth-1],id_b[depth-1])
self.sum(id_c[depth-1],id_a[depth-1],id_b[depth-1])
for i in reversed(range(depth-1)):
self.i_carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.sum(id_c[i],id_a[i],id_b[i])
return self
def arrow(self,N,q,id):
for i in range(len(id)):
if (N>>i)%2 == 1:
self.cx(q,id[i])
return self
def arrow2(self,i,a,id_ctr,id_x,id_xx):
aa = a * 2**i
for j in range(len(id_xx)):
if (aa>>j)%2 == 1:
self.ccx(id_ctr[0],id_x[i],id_xx[j])
return self
def arrow3(self,id_ctr,id_x,id_y):
for j in range(len(id_x)):
self.ccx(id_ctr[0],id_x[j],id_y[j])
return self
def i_plain_adder(self,id_a,id_b,id_c):
depth = len(id_a)
for i in range(depth-1):
self.i_sum(id_c[i],id_a[i],id_b[i])
self.carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.i_sum(id_c[depth-1],id_a[depth-1],id_b[depth-1])
self.cx(id_a[depth-1],id_b[depth-1])
for i in reversed(range(depth)):
self.i_carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
return self
def modular_adder(self,N,id_a,id_b,id_c,id_N,id_t):
self.plain_adder(id_a,id_b,id_c)
self.swap(id_a,id_N)
self.i_plain_adder(id_a,id_b,id_c)
self.x(id_b[len(id_b)-1])
self.cx(id_b[len(id_b)-1],id_t[0])
self.x(id_b[len(id_b)-1])
self.arrow(N,id_t[0],id_a)
self.plain_adder(id_a,id_b,id_c)
self.arrow(N,id_t[0],id_a)
self.swap(id_a,id_N)
self.i_plain_adder(id_a,id_b,id_c)
self.cx(id_b[len(id_b)-1],id_t[0])
self.plain_adder(id_a,id_b,id_c)
return self
def ctr_modular_multiplier(self,a,N,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t):
depth = len(id_x)
for i in range(depth):
self.arrow2(i,a,id_ctr,id_x,id_xx)
self.modular_adder(N,id_xx,id_y,id_c,id_N,id_t)
self.arrow2(i,a,id_ctr,id_x,id_xx)
self.x(id_ctr[0])
self.arrow3(id_ctr,id_x,id_y)
self.x(id_ctr[0])
return self
def encode(self,decimal,id):
for i in range(len(id)):
if (decimal>>i)%2 == 1:
self.x(id[i])
return self
def create_register(digits):
num = 0
id_ctr = [i for i in range(1)]
num += len(id_ctr)
id_x = [i+num for i in range(digits)]
num += len(id_x)
id_xx = [i+num for i in range(2*digits-1)]
num += len(id_xx)
id_y = [i+num for i in range(2*digits)]
num += len(id_y)
id_c = [i+num for i in range(2*digits)]
id_c[2*digits-1] = id_y[2*digits-1]
num += (len(id_c)-1)
id_N = [i+num for i in range(2*digits-1)]
num += len(id_N)
id_t = [i+num for i in range(1)]
num += len(id_t)
id_r = id_y[:-1]
return (num,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t,id_r)
def superposition(self,id):
for i in range(len(id)):
self.h(id[i])
return self
def result(self,id_a,id_b):
# measurement
id_ab = id_a + id_b
iid_ab = id_ab[::-1]
freq = self.m(id=iid_ab).frq
# set results
a_list = []
r_list = []
for i in range(len(freq)):
if freq[i] > 0:
a_list.append(i%(2**len(id_a)))
r_list.append(i>>len(id_a))
return (a_list,r_list)
if __name__ == '__main__':
# add methods
QState.swap = swap
QState.sum = sum
QState.i_sum = i_sum
QState.carry = carry
QState.i_carry = i_carry
QState.arrow = arrow
QState.arrow2 = arrow2
QState.arrow3 = arrow3
QState.plain_adder = plain_adder
QState.i_plain_adder = i_plain_adder
QState.modular_adder = modular_adder
QState.ctr_modular_multiplier = ctr_modular_multiplier
QState.encode = encode
QState.superposition = superposition
QState.result = result
# create registers
digits = 2
num,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t,id_r = create_register(digits)
# set input numbers
# ctr = 0
ctr = 1
a = 3
N = 5
# initialize quantum state
qs = QState(num)
qs.encode(ctr,id_ctr)
qs.superposition(id_x) # set superposition of |0>,|1>,|2>,|3> for |x>
qs.encode(N,id_N)
# execute controlled modular multiplier
qs.ctr_modular_multiplier(a,N,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t)
x_list,r_list = qs.result(id_x,id_r)
for i in range(len(x_list)):
print("(ctr={0:}) {1:}*{2:} mod {3:} -> {4:}".format(ctr,a,x_list[i],N,r_list[i]))
qs.free()
何をやっているかを説明します。ただし、前々回、前回で出てきた関数については、説明を省略します。
まず、
def arrow2(self,i,a,id_ctr,id_x,id_xx):
aa = a * 2**i
for j in range(len(id_xx)):
if (aa>>j)%2 == 1:
self.ccx(id_ctr[0],id_x[i],id_xx[j])
return self
で、アロー演算子2を定義しています。2つの制御ビットがともに1だった場合のみ、Toffoliゲートをかけているのですが、そのターゲットとなるビット番号は、$2^{i} a$を2進数としたときに1が立っている桁です。こうすることで、レジスタ<xx>に$2^{i} a$が入ることになります。言うまでもないですが、この演算子をもう一回かけると状態は元に戻ります。
def arrow3(self,id_ctr,id_x,id_y):
for j in range(len(id_x)):
self.ccx(id_ctr[0],id_x[j],id_y[j])
return self
アロー演算子3を定義しています。制御ビットが1であり、かつ、レジスタ<x>のj番目のビットが1の場合のみ、レジスタ<y>のj番目のビットを反転させます。これを実現するため、Toffoliゲートを繰り返し使っています。
def ctr_modular_multiplier(self,a,N,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t):
depth = len(id_x)
for i in range(depth):
self.arrow2(i,a,id_ctr,id_x,id_xx)
self.modular_adder(N,id_xx,id_y,id_c,id_N,id_t)
self.arrow2(i,a,id_ctr,id_x,id_xx)
self.x(id_ctr[0])
self.arrow3(id_ctr,id_x,id_y)
self.x(id_ctr[0])
return self
で、制御-剰余乗算を定義しています。上の回路図をそのまま順に実行しているだけです。
というわけで、プログラム本体の説明です。
# create registers
digits = 2
num,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t,id_r = create_register(digits)
で、各レジスタを定義して、必要となる全体量子ビット数を計算して、適当な変数に格納しています。関数create_registerの説明はしていませんでしたが、前々回、前回と同じようなものを今回用に作れば良いだけです。
# set input numbers
# ctr = 0
ctr = 1
a = 3
N = 5
# initialize quantum state
qs = QState(num)
qs.encode(ctr,id_ctr)
qs.superposition(id_x) # set superposition of |0>,|1>,|2>,|3> for |x>
qs.encode(N,id_N)
今回、固定入力するa,Nの値および制御ビットctrの値を設定し、xについては取りうる値すべての重ね合わせ状態とします。
# execute controlled modular multiplier
qs.ctr_modular_multiplier(a,N,id_ctr,id_x,id_xx,id_y,id_c,id_N,id_t)
制御-剰余乗算を実行します。
x_list,r_list = qs.result(id_x,id_r)
for i in range(len(x_list)):
print("(ctr={0:}) {1:}*{2:} mod {3:} -> {4:}".format(ctr,a,x_list[i],N,r_list[i]))
測定によって得られた結果から、レジスタ<x>の状態とレジスタ<r>(=レジスタ<y>)の状態をセットにして表示します。$ctr,a,N$は、設定した値をそのまま表示します。
実行結果は、以下の通りです。制御ビットを1にすると、
(ctr=1) 3*0 mod 5 -> 0
(ctr=1) 3*2 mod 5 -> 1
(ctr=1) 3*1 mod 5 -> 3
(ctr=1) 3*3 mod 5 -> 4
となります。制御ビットを0にすると、
(ctr=0) 3*0 mod 5 -> 0
(ctr=0) 3*1 mod 5 -> 1
(ctr=0) 3*2 mod 5 -> 2
(ctr=0) 3*3 mod 5 -> 3
となります。というわけで、制御-剰余乗算が正しく計算できることが確認できました。
おわりに
加算と剰余加算を部品にして、とりあえず何とかシミュレータで動作確認ができました。回路図には明示的に表現されていない補助的な量子ビットが結構必要になるので、わずか2ビットの計算をするのに、17量子ビットも必要となりました(自分の見積もりが間違っていなければ)。次回は、いよいよ「べき剰余」に挑戦ですが、できる範囲で何とか頑張ってみようと思います。
以上