$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
はじめに
前々回の記事で「量子フーリエ変換」、前回の記事で「位相推定アルゴリズム」の確認ができたので、次は「Shorのアルゴリズム」と思っていたら、「べき剰余」も必要なのでした。で、べき剰余を実行するためには、いくつかの算術演算の基礎も必要ということなので、以後しばらくは、算術演算を順に確認していこうと思います。今回はもっとも簡単な「加算」です。アルゴリズムを説明した後、自作の量子計算シミュレータqlazyで、動作の確認をします。
参考にさせていただいた論文・記事は以下の通りです。
- V. Vedral,A. Barenco,A. Ekert; "Quantum Networks for Elementary Arithmetic Operations" (arXiv:quant-ph/9511018)
- 量子コンピュータ(シミュレータ)でモジュール化可能な加算器を作る
加算の実現方法
参考論文に全体の回路図が出ているので、まずそれを掲載します。

論文には、
\ket{a,b} \rightarrow \ket{a,a+b}
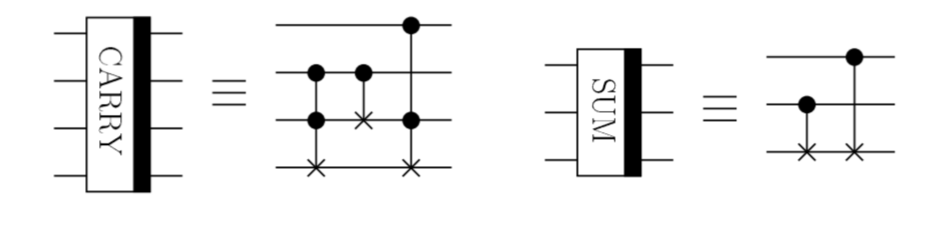
を計算する回路と説明されています。ここで、$a_0,a_1,...$と$b_0,b_1,...$は、整数$a,b$を2進数で表したときの各桁の値{0,1}を下の桁から順に並べた数列です。$c_0,c_1,...$は、各桁を加算したときに発生する桁上げ情報を格納するための補助量子ビットです。また、CARRYとSUMと書いてあるボックスは各々以下のような量子回路で定義されます。
これで本当に加算が実現できるのでしょうか。まずは各部品(CARRYとSUM)の動作から地道に見ていくことにします。
CARRYの動作
CARRYの量子レジスタは4つあり、1つのCNOTゲートと2つのToffoliゲートから構成されています。入力状態を上から$\ket{x},\ket{y},\ket{z},\ket{w}$としたとき、最初のToffoliゲート、CNOTゲート、2番目のToffoliゲートを通っていくに従い、どのように状態が変化するかを以下の表に示してみます。
| 初期状態 | Toffoli[1] | CNOT | Toffoli[2] |
|---|---|---|---|
| $x$ | $x$ | $x$ | $x$ |
| $y$ | $y$ | $y$ | $y$ |
| $z$ | $z$ | $y \oplus z$ | $y \oplus z$ |
| $w$ | $(yz) \oplus w$ | $(yz) \oplus w$ | $(xy \oplus yz \oplus zx) \oplus w$ |
最終的に$x,y$のレジスタは変化せず、$z$のレジスタには$y,z$の加算(ただしmod 2)が入り、一番下のレジスタは、
\ket{w} \rightarrow \ket{(xy \oplus yz \oplus zx) \oplus w}
となることがわかります。ここで、$(xy \oplus yz \oplus zx)$は、$x,y,z$のどれか2つ以上が1をとるときに1になり、そうでない場合0になります。ということは、$x,y,z$を全部足した結果、桁上げがある場合、$\ket{1 \oplus w}$、桁上げがない場合$\ket{0 \oplus w}$となりますので、一番下のレジスタは桁上げを表していると言えそうです。
改めて全体の回路図を見てみてください。CARRYの入力レジスタの状態は$c_{i},a_{i},b_{i},c_{i+1}$となっていますので、$a$と$b$の$i$番目の桁を足して、さらに$i-1$番目までの桁から来る桁上げの値(0または1)を足したものが、$c_{i+1}$のレジスタに入ります。どうでしょう。加算の桁上げの役割を果たしているような気がしてきますよね。
後の議論のため、上の表の記号を$x,y,z,w$ではなく、$c_{i},a_{i},b_{i},c_{i+1}$に変えて記載しておきます。
| 初期状態 | Toffoli[1] | CNOT | Toffoli[2] |
|---|---|---|---|
| $c_{i}$ | $c_{i}$ | $c_{i}$ | $c_{i}$ |
| $a_{i}$ | $a_{i}$ | $a_{i}$ | $a_{i}$ |
| $b_{i}$ | $b_{i}$ | $a_{i} \oplus b_{i}$ | $a_{i} \oplus b_{i}$ |
| $c_{i+1}$ | $(a_{i}b_{i}) \oplus c_{i+1}$ | $(a_{i}b_{i}) \oplus c_{i+1}$ | $c_{i+1}^{\prime}$ |
ここで、
c_{i+1}^{\prime} = (c_{i}a_{i} \oplus a_{i}b_{i} \oplus b_{i}c_{i}) \oplus c_{i+1}
とおきました。つまり、$c_{i}^{\prime}$は下の桁からやってくる桁上げの値を表しています。
ついでに、CARRYの逆演算(以下i-CARRYと呼ぶことにします)も見てみましょう。上の表を逆から読むだけです。
| 初期状態 | Toffoli[2] | CNOT | Toffoli[1] |
|---|---|---|---|
| $c_{i}$ | $c_{i}$ | $c_{i}$ | $c_{i}$ |
| $a_{i}$ | $a_{i}$ | $a_{i}$ | $a_{i}$ |
| $a_{i} \oplus b_{i}$ | $a_{i} \oplus b_{i}$ | $b_{i}$ | $b_{i}$ |
| $c_{i}^{\prime}$ | $(a_{i}b_{i}) \oplus c_{i+1}$ | $(a_{i}b_{i}) \oplus c_{i+1}$ | $c_{i+1}$ |
となります。
SUMの動作
SUMは簡単です。3つの量子レジスタに対する入力を$c_{i},a_{i},b_{i}$とすると、量子状態は以下のように変化します。
| 初期状態 | CNOT[1] | CNOT[2] |
|---|---|---|
| $c_{i}$ | $c_{i}$ | $c_{i}$ |
| $a_{i}$ | $a_{i}$ | $a_{i}$ |
| $b_{i}$ | $a_{i} \oplus b_{i}$ | $a_{i} \oplus b_{i} \oplus c_{i}$ |
ということで、$b_{i}$のレジスタに下の桁の桁上げも含めた加算(ただしmod 2)の結果が入ることがわかります。つまり、SUMは各桁の加算を表しています。
1量子ビットの加算
部品の動作が確認できたところで、これを組み合わせて本当に$a+b$が実行できるかを、具体的に確認してみます。まずは1量子ビットの場合です。全体の回路図を参照すると、$a,b$各々の入力が1量子ビットの場合は、以下のような回路になります。
c0=0 ---|C||------|S||--- c0=0
a0 ---|A||--*---|U||--- a0
b0 ---|R||--CX--|M||--- b0
c1=0 ---|R||------------- b1
各部品の動作を表す上の表を参照しながら、この回路での状態変化を表にすると、
| 初期状態 | CARRY | CNOT | SUM |
|---|---|---|---|
| $c_{0}=0$ | $c_{0}=0$ | $c_{0}=0$ | $c_{0}=0$ |
| $a_{0}$ | $a_{0}$ | $a_{0}$ | $a_{0}$ |
| $b_{0}$ | $a_{0} \oplus b_{0}$ | $b_{0}$ | $a_{0} \oplus b_{0}$ |
| $c_{1}=0$ | $c_{1}^{\prime}$ | $c_{1}^{\prime}$ | $c_{1}^{\prime} = b_{1}$ |
となります。この最終状態でレジスタ($b_{0},b_{1}$)を観測すると、ちょうど$a+b$を実行した結果に等しくなることがわかると思います(ここで$b_{0}$は下位、$b_{1}$は上位ビットを表します。この加算回路では補助量子ビット$c$の最上位を$b$の最上位ビットと同一視するようにしています)。
2量子ビットの加算
次に、2量子ビットです。回路図は、以下の通りです。
c0=0 --|C||------------------||C|--|S||-- c0=0
a0 --|A||------------------||A|--|U||-- a0
b0 --|R||------------------||R|--|M||-- b0
c1=0 --|R||--|C||------|S||--||R|-------- c1=0
a1 --------|A||--*---|U||-------------- a1
b1 --------|R||--CX--|M||-------------- b1
c2=0 --------|R||------------------------ b2
先程と同様に、状態変化を表にしてみます。
| 初期状態 | 1番目のCARRY | 2番目のCARRY | CNOT | 1番目のSUM | i-CARRY | 2番目のSUM |
|---|---|---|---|---|---|---|
| $c_{0}=0$ | $c_{0}$ | $c_{0}$ | $c_{0}$ | $c_{0}$ | $c_{0}$ | $c_{0}=0$ |
| $a_{0}$ | $a_{0}$ | $a_{0}$ | $a_{0}$ | $a_{0}$ | $a_{0}$ | $a_{0}$ |
| $b_{0}$ | $a_{0} \oplus b_{0}$ | $a_{0} \oplus b_{0}$ | $a_{0} \oplus b_{0}$ | $a_{0} \oplus b_{0}$ | $b_{0}$ | $a_{0} \oplus b_{0}$ |
| $c_{1}=0$ | $c_{1}^{\prime}$ | $c_{1}^{\prime}$ | $c_{1}^{\prime}$ | $c_{1}^{\prime}$ | $c_{1}$ | $c_{1}=0$ |
| $a_{1}$ | $a_{1}$ | $a_{1}$ | $a_{1}$ | $a_{1}$ | $a_{1}$ | $a_{1}$ |
| $b_{1}$ | $b_{1}$ | $a_{1} \oplus b_{1}$ | $b_{1}$ | $c_{1}^{\prime} \oplus a_{1} \oplus b_{1}$ | $c_{1}^{\prime} \oplus a_{1} \oplus b_{1}$ | $c_{1}^{\prime} \oplus a_{1} \oplus b_{1}$ |
| $c_{2}=0$ | $c_{2}$ | $c_{2}^{\prime}$ | $c_{2}^{\prime}$ | $c_{2}^{\prime}$ | $c_{2}^{\prime}$ | $c_{2}^{\prime}=b_{2}$ |
となります。この最終状態でレジスタ($b_{0},b_{1},b_{2}$)を観測すると、ちょうど$a+b$を実行した結果に等しくなることがわかります。
N量子ビットの加算
3量子ビット以上の場合は、上の議論を延長してちょっと考えてみれば、確かに足し算を実行していることがわかります(2進数の足し算を筆算でやることを頭の中でイメージしていただければ、わかりやすいと思います)。
シミュレータで動作確認
重ね合わせ無し
さて、それではシミュレータで、この加算の動作を確認してみます。まず、重ね合わせがない一つの純粋状態を入力した場合です。全体のPythonコードは以下の通りです。
【2021.9.5補足】qlazy最新版でのソースコードはここに置いてあります。
from qlazypy import QState
def sum(self,q0,q1,q2):
self.cx(q1,q2).cx(q0,q2)
return self
def carry(self,q0,q1,q2,q3):
self.ccx(q1,q2,q3).cx(q1,q2).ccx(q0,q2,q3)
return self
def i_carry(self,q0,q1,q2,q3):
self.ccx(q0,q2,q3).cx(q1,q2).ccx(q1,q2,q3)
return self
def plain_adder(self,id_a,id_b,id_c):
depth = len(id_a)
for i in range(depth):
self.carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.cx(id_a[depth-1],id_b[depth-1])
self.sum(id_c[depth-1],id_a[depth-1],id_b[depth-1])
for i in reversed(range(depth-1)):
self.i_carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.sum(id_c[i],id_a[i],id_b[i])
return self
def encode(self,decimal,id):
for i in range(len(id)):
if (decimal>>i)%2 == 1:
self.x(id[i])
return self
def decode(self,id):
iid = id[::-1]
return self.m(id=iid,shots=1).lst
def create_register(digits):
num = 0
id_a = [i for i in range(digits)]
num += len(id_a)
id_b = [i+num for i in range(digits+1)]
num += len(id_b)
id_c = [i+num for i in range(digits+1)]
id_c[digits] = id_b[digits] # share the qubit id's
num += (len(id_c)-1)
return (num,id_a,id_b,id_c)
if __name__ == '__main__':
# add metthods
QState.encode = encode
QState.decode = decode
QState.sum = sum
QState.carry = carry
QState.i_carry = i_carry
QState.plain_adder = plain_adder
# create registers
digits = 4
num,id_a,id_b,id_c = create_register(digits)
# set input numbers
a_list = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
b = 12
for a in a_list:
# initialize quantum state
qs = QState(num)
qs.encode(a,id_a)
qs.encode(b,id_b)
# execute plain adder
qs.plain_adder(id_a,id_b,id_c)
res = qs.decode(id_b)
print("{0:}+{1:} -> {2:}".format(a,b,res))
qs.free()
何をやっているか簡単に説明します。
def sum(self,q0,q1,q2):
self.cx(q1,q2).cx(q0,q2)
return self
def carry(self,q0,q1,q2,q3):
self.ccx(q1,q2,q3).cx(q1,q2).ccx(q0,q2,q3)
return self
def i_carry(self,q0,q1,q2,q3):
self.ccx(q0,q2,q3).cx(q1,q2).ccx(q1,q2,q3)
return self
で、上で説明したCARRY,i-CARRY,SUMの動作を関数として定義しています。QStateクラスのメソッドとして動的追加することを想定し、第1引数をselfにしています。
def plain_adder(self,id_a,id_b,id_c):
depth = len(id_a)
for i in range(depth):
self.carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.cx(id_a[depth-1],id_b[depth-1])
self.sum(id_c[depth-1],id_a[depth-1],id_b[depth-1])
for i in reversed(range(depth-1)):
self.i_carry(id_c[i],id_a[i],id_b[i],id_c[i+1])
self.sum(id_c[i],id_a[i],id_b[i])
return self
で、それら部品関数を組み合わせた加算器をplain_adder関数として定義しています。これも、QStateクラスのメソッドとして動的追加するため、第1引数はselfです。第2引数以降のid_a,id_b,id_cはそれぞれa,b,cに対応した量子レジスタ番号のリストを表しています(量子レジスタの生成は別の関数create_registerで行います)。関数内部の処理は、上で説明した回路図そのものです。
def encode(self,decimal,id):
for i in range(len(id)):
if (decimal>>i)%2 == 1:
self.x(id[i])
return self
は、入力量子ビットを設定する関数です。decimalという10進整数を、量子レジスタidに設定します(つまり、量子レジスタidを$\ket{desimal}$という状態にします)。関数内部では、decimalを2進数に直してビットが立っている桁に相当する量子レジスタのビットをXゲートで反転しています。
def decode(self,id):
iid = id[::-1]
return self.m(id=iid,shots=1).lst
は、encodeと逆に最終状態の量子レジスタidを観測して得られた{0,1}系列から10進整数を構成してリターンします。idに相当する量子ビットだけを1回観測し、lstプロパティによってその結果(10進整数)を得ています。
def create_register(digits):
num = 0
id_a = [i for i in range(digits)]
num += len(id_a)
id_b = [i+num for i in range(digits+1)]
num += len(id_b)
id_c = [i+num for i in range(digits+1)]
id_c[digits] = id_b[digits] # share the qubit id's
num += (len(id_c)-1)
return (num,id_a,id_b,id_c)
は、今回の量子レジスタの配置を決めてそのリストおよび全体で必要となる量子ビット数をリターンする関数です。digitsは入力として想定するビット数です。
一連の関数が定義できたところで、プログラムのmain部を見ていきます。まず、
QState.encode = encode
QState.decode = decode
QState.sum = sum
QState.carry = carry
QState.i_carry = i_carry
QState.plain_adder = plain_adder
で、上で定義した関数を、QStateクラスのメソッドとして追加しています。
digits = 4
num,id_a,id_b,id_c = create_register(digits)
で、量子レジスタを決定して変数num,id_a,id_b,id_cに格納しています。量子計算(加算)の実体部分は以下です。
# set input numbers
a_list = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
b = 12
for a in a_list:
# initialize quantum state
qs = QState(num)
qs.encode(a,id_a)
qs.encode(b,id_b)
# execute plain adder
qs.plain_adder(id_a,id_b,id_c)
res = qs.decode(id_b)
print("{0:}+{1:} -> {2:}".format(a,b,res))
qs.free()
量子ビット数はdigit=4と設定してあるので、4ビット同士の加算を実行します。ここでは、aの値を0から15まで変化させながら、固定値b=12との足し算結果を表示します。
実行結果を以下に示します。
0+12 -> 12
1+12 -> 13
2+12 -> 14
3+12 -> 15
4+12 -> 16
5+12 -> 17
6+12 -> 18
7+12 -> 19
8+12 -> 20
9+12 -> 21
10+12 -> 22
11+12 -> 23
12+12 -> 24
13+12 -> 25
14+12 -> 26
15+12 -> 27
というわけで、正しく計算できることがわかりました。
重ね合わせ有り
さて、上に示したように逐次実行するのは、実は、あまり賢いやり方ではありません。量子計算では、入力値を量子重ね合わせとして用意しておけば、逐次的にぐるぐるforループを回さなくても、多数の入力値を一気に計算することができます。というわけで、やってみます。
【2021.9.5補足】qlazy最新版でのソースコードはここに置いてあります。
まず、先程のencode関数の代わりに、
def superposition(self,id):
for i in range(len(id)):
self.h(id[i])
return self
という、入力状態を重ね合わせとして用意する関数superpositionを定義します。内部では引数として指定した量子レジスタのすべてに対してアダマールをかけています。入力が重ね合わせなので、出力も重ね合わせになります。そこから結果を引き出す関数も必要になるので、以下のように定義します。
def result(self,id_a,id_b):
# measurement
id_ab = id_a + id_b
iid_ab = id_ab[::-1]
freq = self.m(id=iid_ab).frq
# set results
a_list = []
r_list = []
for i in range(len(freq)):
if freq[i] > 0:
a_list.append(i%(2**len(id_a)))
r_list.append(i>>len(id_a))
return (a_list,r_list)
プログラムのmain部は以下のようになります。「重ね合わせなし」の場合との違いに注目してください。forループがないですよね。先程は15回、量子状態を初期化して量子計算をぐるぐると実行しましたが、今回は1回しか実行していません。
if __name__ == '__main__':
# add methods
QState.encode = encode
QState.decode = decode
QState.sum = sum
QState.carry = carry
QState.i_carry = i_carry
QState.plain_adder = plain_adder
# add methods (for superposition)
QState.superposition = superposition
QState.result = result
# create registers
digits = 4
num,id_a,id_b,id_c = create_register(digits)
# set input numbers
b = 12
# initialize quantum state
qs = QState(num)
qs.superposition(id_a) # set superposition of |0>,|1>,..,|15> for |a>
qs.encode(b,id_b)
# execute plain adder
qs.plain_adder(id_a,id_b,id_c)
a_list,r_list = qs.result(id_a,id_b)
for i in range(len(a_list)):
print("{0:}+{1:} -> {2:}".format(a_list[i],b,r_list[i]))
qs.free()
結果は以下の通りです。
0+12 -> 12
1+12 -> 13
2+12 -> 14
3+12 -> 15
4+12 -> 16
5+12 -> 17
6+12 -> 18
7+12 -> 19
8+12 -> 20
9+12 -> 21
10+12 -> 22
11+12 -> 23
12+12 -> 24
13+12 -> 25
14+12 -> 26
15+12 -> 27
というわけで、4ビットのaの値すべてに対して一気に加算が実行できました。めでたしめでたし、と言いたいところですが、注意しておきたいことが一つあります。一気に結果が表示できるように見せかけていますが、これはシミュレータだからできることでありまして、実際の量子コンピュータでは、こんなことはできません。最終的な量子状態に対して測定をしたらば、基本一つの結果しか得られません。例えば"5+12->17"でした、という結果です。すべての加算結果を得るためには、やはり何度も何度も入力状態を用意して測定する必要があります。「なーんだ、量子コンピュータ、速くないじゃん」と思われるかもしれませんが、この例の場合は、確かにその通りかもしれません。
実際の量子計算では、求めたい結果に相当する状態の確率がなるべく高くなるように量子回路を構成し最後に測定することで、何度も計算実行しなくても、欲しい結果を効率よく得られるようにしています。量子アルゴリズムがこれまでにいろいろと提案されていますが、ざっくり言うと、要はそういうことをやっているわけです。
おわりに
今回、算術演算の中でもっとも簡単な「加算」の動作を確認しました。「Shorのアルゴリズム」で必要になる「べき剰余」に至るまで、あと何ステップかありますが、参考論文に従い、以後、順に確認していこうと思います。具体的には「剰余加算」→「制御剰余乗算」→「べき剰余」を予定しています。果たして最終ゴールまでたどり着けるかどうか...。ちょっとドキドキしてきましたが、何とか(できるところまでかもしれませんが)頑張ってみたいと思います。
以上