はじめに
(注)
私は量子情報の専門家でも,情報の専門家でもありません。勉強している身です。不適切な表現あるいは誤り等ございましたらご指摘いただけると幸いです。
前回の記事ではIBM Qを用いて量子フーリエ変換を実行してみました。
そもそも,量子フーリエ変換をしたかった理由は,最終的にショアのアルゴリズムを自分でプログラムしたかったからです。
その第一歩が,量子フーリエ変換(逆量子フーリエ変換)を実行するということでした。
ショアのアルゴリズムは@kyamazさんの記事で分かりやすく説明されていますので,ご興味のある方は是非一読ください。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
注目したいのは,ショアのアルゴリズムのうち,量子オラクル(モジュロ演算)にあたる部分です。
つまり,最終的にはなんとかして,
$$
f(x) = a^x ,,\text{mod},,N
$$
を実行できる量子回路を組みたいわけです。
ショアのアルゴリズムの中で,一番重要かつ一番難しいのがこの部分であろうと私は感じています。
この回路はどうやって組めるのかとかなり苦戦しておりましたが,参考文献を教えていただきその活路が見いだせましたので,その第一弾として,IBM Qのシミュレータ上で加算器を作った経緯を備忘録としてここに記載いたします。
(※文献を教えてくださった「skonb」さんに感謝致します※)
加算器はモジュロ演算器を作るための一番基本的な演算であり,この記事ではモジュール化することが可能な加算器を作ります。
基本的な概念
入力・出力はいくつかのレジスタが必要になります。$f$が入力$x$と$f(x)$との間で1:1対応で,演算が形式的にユニタリ演算子$U_f$として書かれるとき以下のようになります。
$$
U_f\ket{x} \to \ket{f(x)}
$$
実際には,$f$が共役でない場合,補助の役割を果たす量子ビット(以降,補助ビット)が必要になります。
このとき,計算は2つのレジスタのユニタリ変換$U_f$として以下のようにあらわされます。
$$
U_f\ket{x,0} \to \ket{x,f(x)}
$$
ここで,第2レジスタは$f(x)$を収めるために適切なサイズを用意しておく必要があります。
加算
2つのレジスタ$\ket{a}$,$\ket{b}$の加算は,一番簡単な形式では,次のようにあらわされます。
$$
\ket{a,b,0} \to \ket{a,b,a+b}
$$
この記事では,以下のような演算になる量子回路を組むようにします。つまり,入力$\ket{b}$を上書きして出力$\ket{a+b}$を得る加算器を作成します。
$$
\ket{a,b} \to \ket{a,a+b}
$$
出力$(a,a+b)$から入力$(a+b)$を再構成することができるので,情報の損失はなく,計算は可逆的に実行できます。
オーバーフローを防ぐため,出力を格納する第2レジスタ(ここでは$\ket{b}$)は十分に大きい必要があります。
つまり,例えば$a$,$b$が$n$量子ビットでエンコードされるとき,第2レジスタは$n+1$の大きさであるべきです。
また,加算の桁上げを一時的に書き込むための,$\ket{0}$で初期化されるレジスタ$\ket{c}$も必要になります。
今回は,後に図としてわかりやすくするため,オーバーフロー用の1量子ビットを$c$のレジスタの最上位に追加することにしました。結局,$a$,$b$,$c$それぞれの大きさは$n$,$n$,$n+1$です。$c_0$はモジュール化するために必要であり,そのため大きさが$n+1$となっています。
計算手順は以下のようになります。
- まず$a+b$の最上位ビットを計算する。$a_i,b_i,c_i$をそれぞれ第1,第2,一時的な(桁上げ用)レジスタの$(i+1)$番目の量子ビットであるとすると,$c_{i+1} \gets a_{i} ,,\textbf{AND},, b_{i} ,,\textbf{AND},, c_{i}$の演算をすべての$c_i$について実行する。ここで$a$,$b$には加算したい値が入っていて,$c$は$\ket{0}$で初期化されているとする。
- 一時的なレジスタ$c$の最上位のビットを除く各量子ビット$c_i$をすべて初期状態$\ket{0}$に戻す。そのためには,量子ゲートが可逆であることを利用して,$c_i$に対して行った演算をすべて逆に実行する。計算結果は$b_i^{after} \gets a_i ,,\textbf{XOR},, b_i^{before} ,,\textbf{XOR},, c_i$と計算することにより,入力$\ket{b_i}$を上書きする。
上記の量子回路も(可逆の)量子ゲートで構成されていますから,この量子回路全体を反転させた場合,それは減算器になります。たとえば,$a\geq b$の場合,出力は$\ket{a, a-b}$となります。$a3量子ビットの加算器のイメージ
ここでは,具体的に3量子ビットの数$a$,$b$の加算器のイメージ図を示します。上述した手順にしたがうと,以下のようになります。
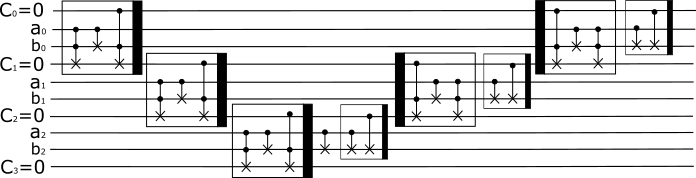
ここで,●印は制御ビット,×印は目標ビットを表しています。制御NOTゲートとトフォリゲートで作成できることがわかりますね。黒に塗りつぶされた枠は参考文献と同様に左右を協調するために使用しました。
IBM Qで実装
IBM Qで実装するにあたり,入力順序をわかりやすくするため整理しました。
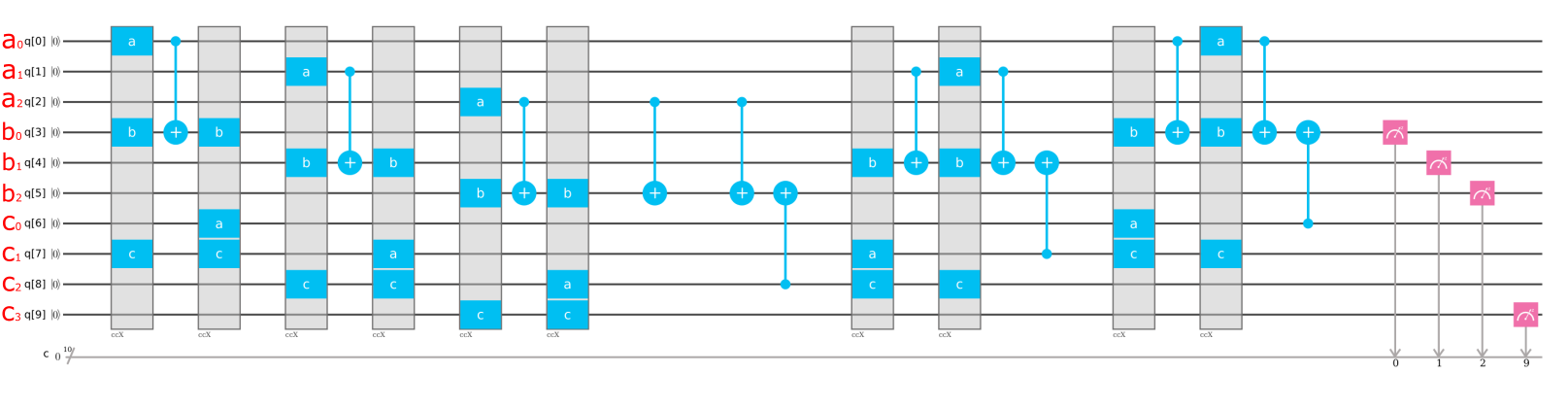
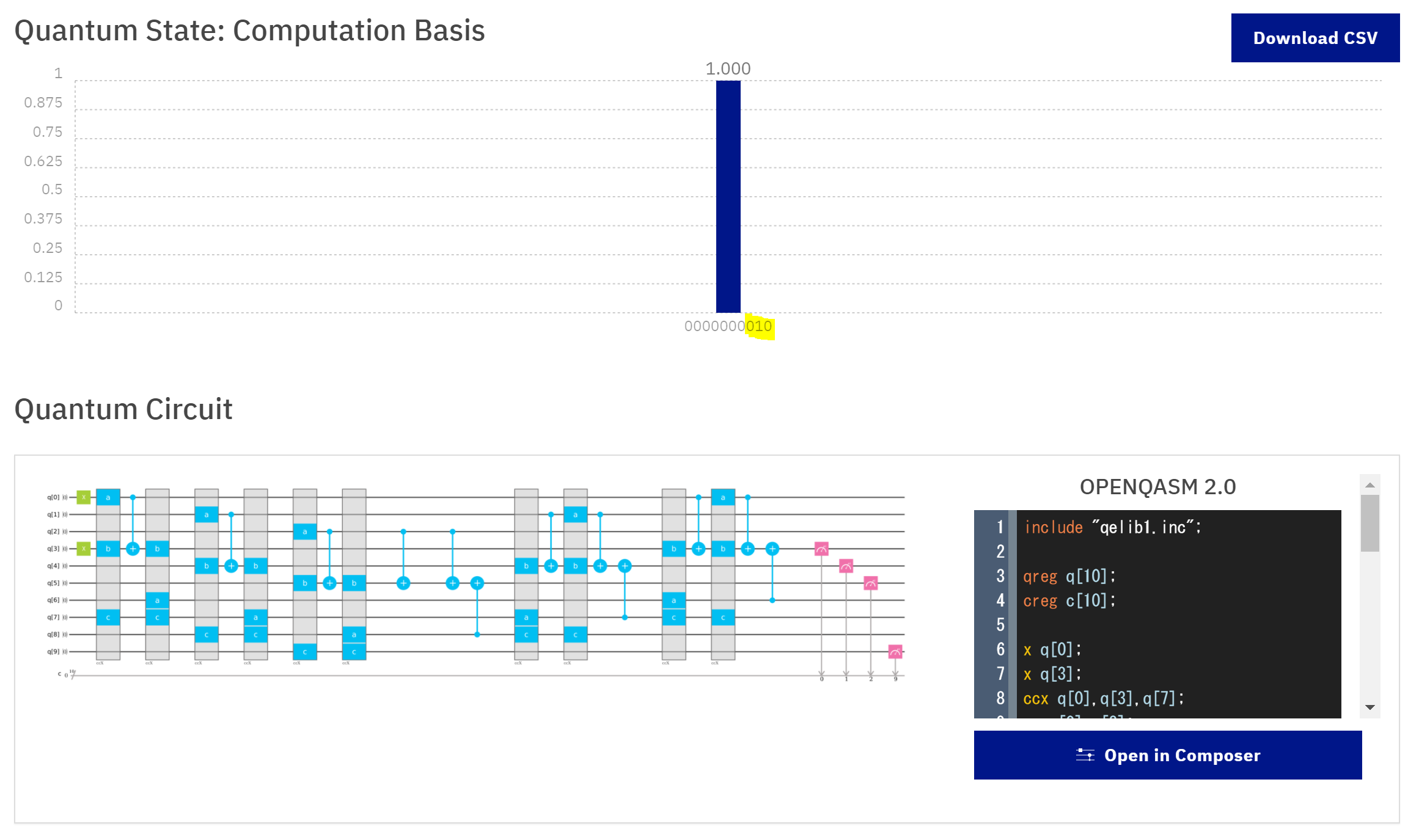
例えば,4+1をしてみます。入力は下のようになります。
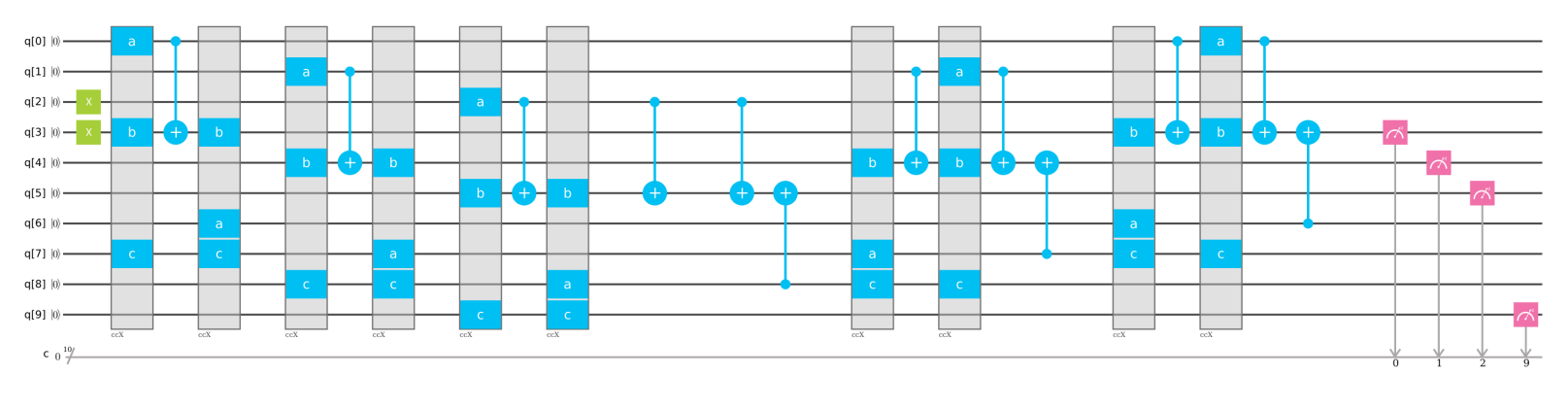
計算結果は以下のようになります。下3桁が計算結果としていますので,$101_2=5$ということになり合っています。
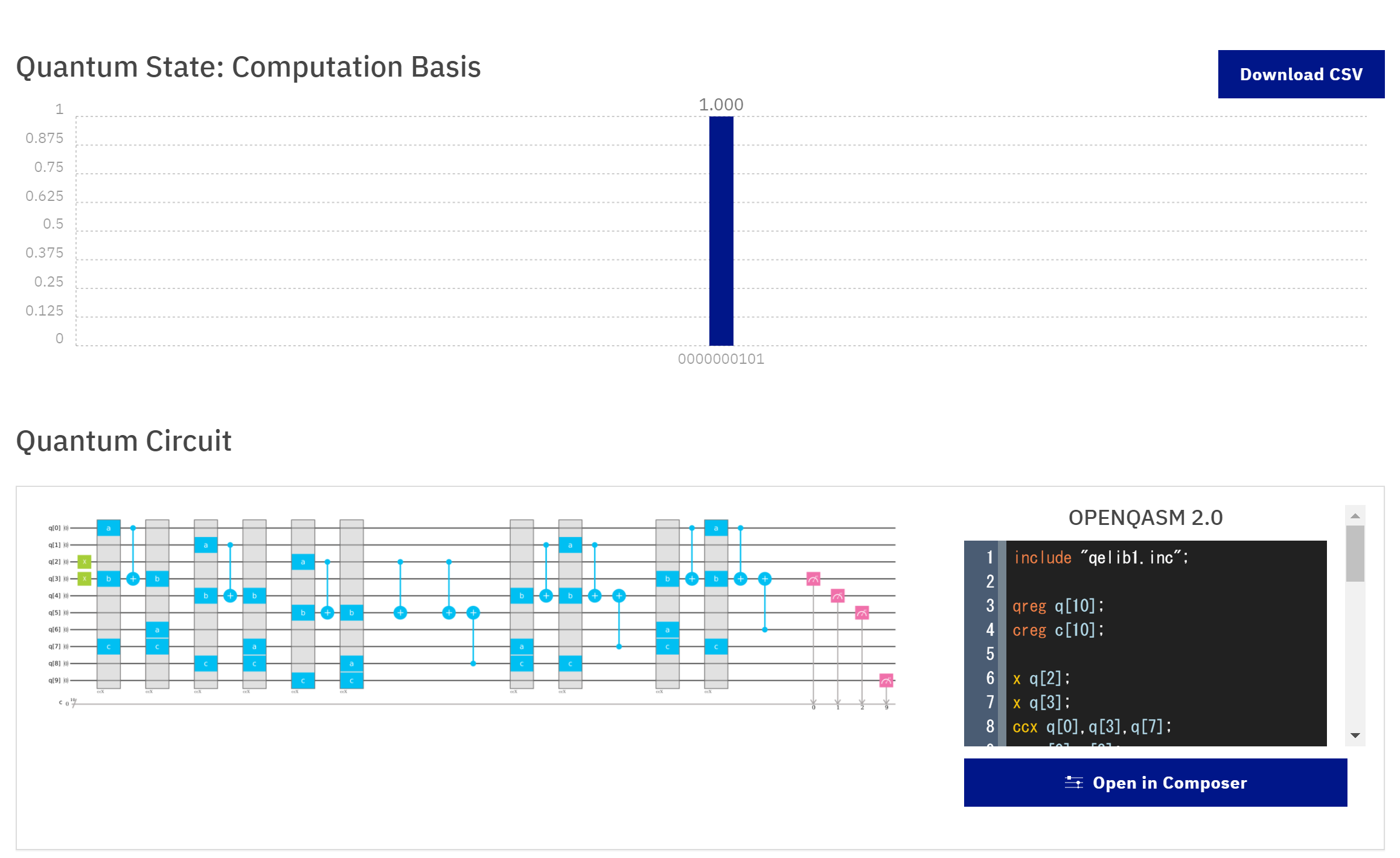
いくつか計算例を示します。
- 2 + 5 = 7  なお,第1レジスタ$\ket{a}$は観測すると,ちゃんと元の値に戻っていることは以下で確認できます。  $\ket{c}$も同様です。オーバーフローしていないので,$\ket{0000}$が確認されるはずですね。 
- 6 + 5 = 11 ??  このように,オーバーフローした場合はフラグが立つようになっています。
おわりに
以上のように,次の演算を実行する加算器が作成できました。
$$
\ket{a,b} \to \ket{a,a+b}
$$
上の例では3量子ビットでしたが,$n$量子ビットでも同様に作成することができます。それらの量子回路をモジュールとして組み合わせることで,モジュロ加算・モジュロ乗算・モジュロ累乗ができるようになります。次回はモジュロ加算(できればモジュロ乗算)について書ければと思います。
ここまで読んでくださってありがとうございました。
参考文献
Vlatko Vedral, Adriano Barenco and Artur Ekert, "Quantum Networks for Elementary Arithmetic Operations"