量子情報理論の基本：Lattice Surgery #Python

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

はじめに

前回の記事で量子誤り訂正符号について一区切り付いたと言いましたが、やはりこれはどうしても外せません。というわけで、今回は「Lattice Surgery」を取り上げます。Braidingは格子状に敷き詰められた量子ビット集団に欠陥対を形成しそれを論理量子ビットと見立てて、欠陥を動き回らせることで論理演算を実現するのでした。物理量子ビットに対する演算はすべて局所的に行われるので（つまり、遠距離にある物理量子ビット同士の演算が一切ないので）、ハードウェア的に無理がない実現方式ではあるのですが¹、いかんせん用意すべき物理量子ビットが膨大になりがちという欠点がありました。それに対して、平面符号（planar code）はBraidingのように量子ビットを浪費しないのですが、論理的な2量子ビット演算を実現しようとするとどうしても量子ビット同士の遠隔演算が必要になるという欠点がありました。Lattice Surgeryは平面符号をベースにしつつ、局所的な量子演算だけで論理的な2量子ビット演算が実現できる、とっても賢い手法です。本記事では、どういった理屈でそんなことができるのかを勉強します。そして、一通り理解できたところで、量子計算シミュレータqlazyを使ってその演算の一例をシミュレーションしてみます。

参考にさせていただいたのは、以下の文献です。

Clare Horseman, Austin G. Flower, Simon Devitt, Rodney Van Meter, "Surface code quantum computing by lattice surgery", arXiv:1111.4022v3 [quant-ph]

理論説明

平面符号(planar code)

まずLattice Surgeryのベースになっている平面符号について説明します。

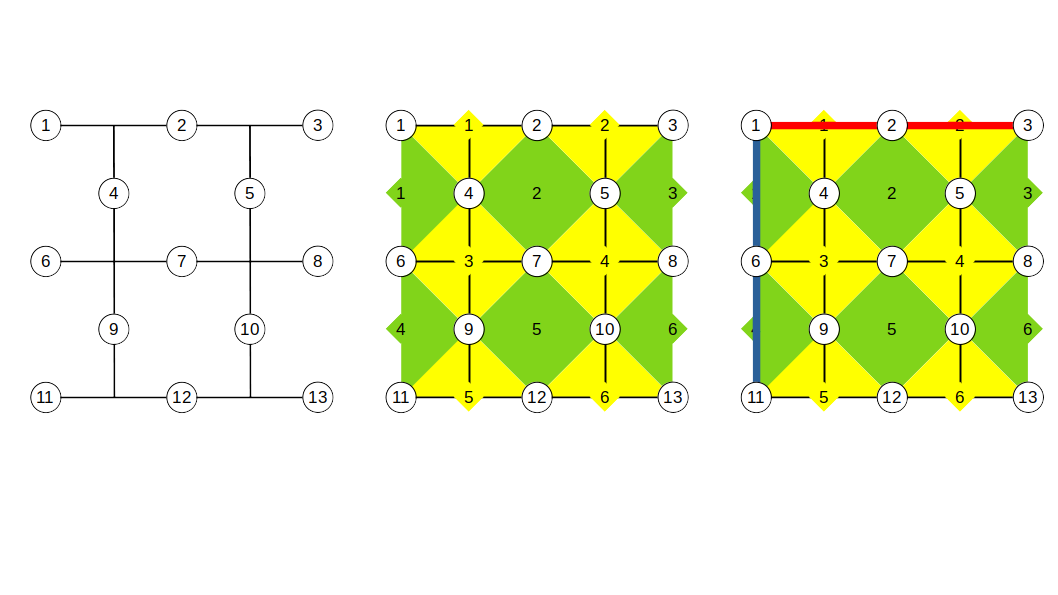
定義

上図左に示すような格子状に量子ビットを並べ、上図中に示したようにスタビライザーを配備します（$X$スタビライザーを黄色、$Z$スタビライザーを緑色で示しました）。それらスタビライザーの同時固有状態を論理符号空間とみなすというのが平面符号です。ここでご注意いただきたいのは、上下の辺に位置するスタビライザーは3端子の$X$スタビライザーになっていて、左右の辺に位置するスタビライザーは3端子の$Z$スタビライザーになっているということです。これが平面符号の特徴です。上下の辺のことを$X$境界（または、smooth boundary）、左右の辺のことを$Z$境界（または、rough boundary）と呼びます。後で、"Lattice"を"Surgery"する際にどっちの境界で考えるかが大事なポイントになりますので覚えておきましょう。さて、上図中には、$6$個の$X$スタビライザーと$6$個の$Z$スタビライザーが存在しますが、各々を$\bar{X_i}, \space \bar{Z_i} \space (i=1,2,\cdots,6)$と表すことにすると、その同時固有状態は、

C = <\bar{X_1}, \bar{X_2}, \cdots, \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \cdots, \bar{Z_6}>  \tag{1}

のようにスタビライザー形式（スタビライザー群の生成元の集まり）で表すことができます。つまり、これら生成元の任意の積を演算しても不変になる状態（同時固有状態）をこの$C$によって規定して、それを論理符号空間とみなすわけです。ここで、$X$スタビライザーの添字は対応した頂点の番号（その$X$スタビライザーを間接測定するためのアンシラの番号）を表しており、$Z$スタビライザーの添字は対応した面の番号（その$Z$スタビライザーを間接測定するためのアンシラの番号）を表していると思ってください（上図では各々黄色と緑色のひし形で表しました）。$\bar{X_i}, \space \bar{Z_i}$を明示的に列挙すると、

\begin{align}
\bar{X_1} &= X_{1} X_{2} X_{4} \\ 
\bar{X_2} &= X_{2} X_{3} X_{5} \\ 
\bar{X_3} &= X_{4} X_{6} X_{7} X_{9} \\ 
\bar{X_4} &= X_{5} X_{7} X_{8} X_{10} \\ 
\bar{X_5} &= X_{9} X_{11} X_{12} \\ 
\bar{X_6} &= X_{10} X_{12} X_{13} \tag{2}
\end{align}

\begin{align}
\bar{Z_1} &= Z_{1} Z_{4} Z_{6} \\ 
\bar{Z_2} &= Z_{2} Z_{4} Z_{5} Z_{7} \\ 
\bar{Z_3} &= Z_{3} Z_{5} Z_{8} \\ 
\bar{Z_4} &= Z_{6} Z_{9} Z_{11} \\ 
\bar{Z_5} &= Z_{7} Z_{9} Z_{10} Z_{12} \\ 
\bar{Z_6} &= Z_{8} Z_{10} Z_{13} \tag{3}
\end{align}

です。いま考えている物理量子ビットの数は13個で、式(1)で示した$X$および$Z$スタビライザーの個数は全部で12個です。1ビット分の自由度が残っているので、これで1つの論理量子ビットを表現できることになります²。

この論理符号空間上にある論理状態を$\ket{\Psi}_{L}$とすると、定義によりこれにスタビライザーを演算しても不変になります。すなわち、

\begin{align}
\bar{X_i} \ket{\Psi}_{L} &= \ket{\Psi}_{L} \\
\bar{Z_i} \ket{\Psi}_{L} &= \ket{\Psi}_{L} \space (i = 1,2,\cdots,6)  \tag{4}
\end{align}

を満たします。別の言い方をすると、ある論理状態に対してどのスタビライザーを間接測定したとしても必ず$+1$という結果が得られます。表面符号においては、この性質を誤り訂正に利用します。つまり、どこかにビット反転エラーまたは位相反転エラーが発生したら、その付近にあるスタビライザーの測定結果が$-1$になるので、エラーが発生した箇所が推定できて、そのビットに逆演算を施すというのが誤り訂正の基本的な考え方でした（詳細は量子情報理論の基本：トポロジカル表面符号をご参照ください）。

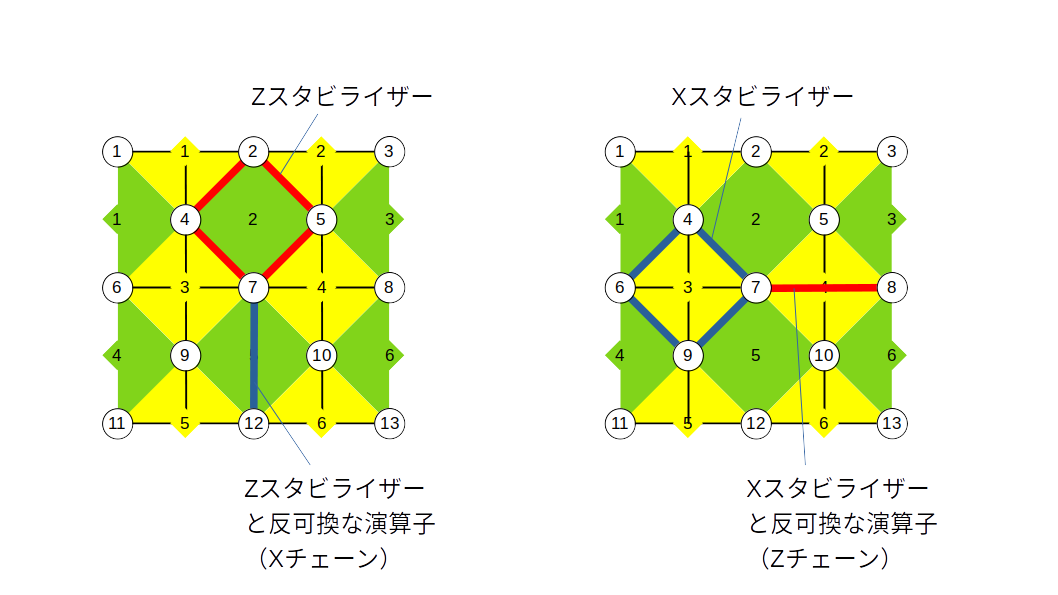
さて、この上で何らかの論理演算を行いたいのですが、それはどのようなものでしょうか。どれか少なくとも一つのスタビライザーと非可換な演算子は式(1)の論理符号空間から状態をはみ出させる効果を持つので、論理演算子にはなり得ません。すべてのスタビライザーと可換な演算子を持ってこないといけないのですが、それをスタビライザーの積で構成してしまうと（つまり式(1)のスタビライザーに従属なものにしてしまうと）、論理状態をまったく変化させませんので、これも論理演算子にはなり得ません。結局、すべてのスタビライザーと可換であり、かつ、それらと独立なものを持ってこないといけません。試しに、そのような演算子のひとつを$Q$とおいてみると、$\bar{X_i} Q \ket{\Psi}_{L} = Q \ket{\Psi}_{L}, \space \bar{Z_i} Q \ket{\Psi}_{L} = Q \ket{\Psi}_{L}$が成り立ち、式(1)のスタビライザーによって状態は不変となり（つまり論理符号空間からはみ出さず）、かつ、$\ket{\Psi}_{L}$とは別の論理状態$Q \ket{\Psi}_{L} \neq \ket{\Psi}_{L}$に変わります。というわけで、確かにこれは論理演算子ということになります。

では、基本的な論理演算子として、論理パウリ$Z$演算子がどのようなものとして定義できるかを考えてみましょう。すべてのスタビライザーと可換で独立な演算子として、何でも良いので適当に$Z_{L}$なるものをもってきて³、それを式(1)で定義された論理符号空間に加えて、

S_{0} = <\bar{X_1}, \bar{X_2}, \cdots, \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \cdots, \bar{Z_6}, Z_{L}>  \tag{5}

という状態を作ってみます。スタビライザー群の生成元の数と物理量子ビット数が一致するので、これで状態はバッチリ特定されることになります。どんな状態に特定されるかというと、式(1)で定義された論理符号空間内の状態であり、かつ、$Z_{L}$の固有値$+1$に対する固有状態になります。この固有状態を論理的な$\ket{0}$状態とみなして$\ket{0}_{L}$と書くことにすると、

Z_{L} \ket{0}_{L} = \ket{0}_{L} \tag{6}

が成り立ちます。また、式(1)に$Z_{L}$を加える代わりに$-Z_{L}$を加えて、

S_{1} = <\bar{X_1}, \bar{X_2}, \cdots, \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \cdots, \bar{Z_6}, -Z_{L}>  \tag{7}

という状態を作ると、これは$Z_{L}$の固有値$-1$に対する固有状態になっていますので、論理的な$\ket{1}$状態とみなして、$\ket{1}_{L}$と書くことにすると、

Z_{L} \ket{1}_{L} = -\ket{1}_{L} \tag{8}

が成り立ちます。どうでしょうか。$Z_{L}$が$Z$演算子のように見えてきますよね。というわけで、この$Z_{L}$を論理パウリ$Z$演算子と定義することにします。あれ？$Z_{L}$って何でもいいものを適当に持ってきたんじゃなかったっけ？こんないい加減な決め方でいいの？という声が聞こえてきそうですが、これでいいんです。つまり、論理的な計算基底をどう決めるかということなのですが、任意性があるという話ですね。ですが、通常は、上図右に示したように左右の$Z$境界（rough boundary）同士を横方向につないだ$Z$演算子の積を論理パウリ演算子$Z_{L} = Z_{1} Z_{2} Z_{3}$として定義したりします⁴（赤色の線で示しました）。

論理パウリ$Z$演算子が定義できたので、次に論理パウリ$X$演算子を定義します。$Z_{L}$と反可換で式(1)のすべてのスタビライザーと可換なものを選べば良いです。上図右で上下の$X$境界（smooth boundary）を縦方向につないだ$X$演算子の積$X_{L} = X_{1} X_{6} X_{11}$をもってくればその条件を満たします（青色の線で示しました）⁵。

$X_{L}$の固有値$+1$および$-1$に対する固有状態$\ket{+}_{L}, \ket{-}_{L}$をスタビライザー形式で書くと、

\begin{align}
S_{+} &= <\bar{X_1}, \bar{X_2}, \cdots, \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \cdots, \bar{Z_6}, X_{L}>  \\
S_{-} &= <\bar{X_1}, \bar{X_2}, \cdots, \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \cdots, \bar{Z_6}, -X_{L}>  \tag{9}
\end{align}

です。ここで、$S_{+}$は$\ket{+}_{L}$、$S_{-}$は$\ket{-}_{L}$を規定するスタビライザー群を表しており、

\begin{align}
X_{L} \ket{+}_{L} &= \ket{+}_{L} \\
X_{L} \ket{-}_{L} &= - \ket{-}_{L} \tag{10}
\end{align}

が成り立っています。また、以上のことから容易に、

\begin{align}
X_{L} \ket{0}_{L} &= \ket{1}_{L} \\
X_{L} \ket{1}_{L} &= \ket{0}_{L} \\
Z_{L} \ket{+}_{L} &= \ket{-}_{L} \\
Z_{L} \ket{-}_{L} &= \ket{+}_{L} \tag{11}
\end{align}

が示せますので、$X_{L}$、$Z_{L}$は各々論理符号空間上でのビット反転演算子、位相反転演算子と思って良いです。さらに式(11)より、$\ket{+}_{L}$は$\ket{0}_{L}$と$\ket{1}_{L}$を足したものに比例していて、$\ket{+}_{L}$は$\ket{0}_{L}$から$\ket{1}_{L}$を引いたものに比例していることがわかり、各々1に正規化されているとすると、

\begin{align}
\ket{+}_{L} &= \frac{1}{\sqrt{2}} (\ket{0}_{L} + \ket{1}_{L}) \\
\ket{-}_{L} &= \frac{1}{\sqrt{2}} (\ket{0}_{L} - \ket{1}_{L}) \tag{12}
\end{align}

が成り立ちます。

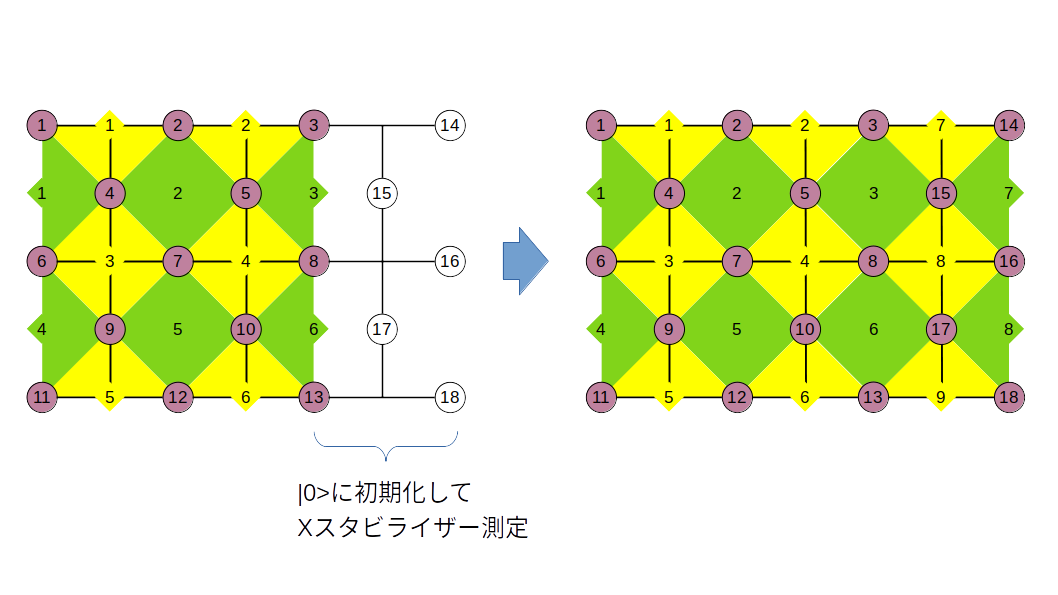
初期状態の作成

実際に平面符号で論理演算を行うためには、最初に式(5)で示したような初期論理状態を作成する必要があります。さて、どうすれば良いでしょうか。とにかく式(5)上でズラッと並んだ生成元に対する同時固有状態を作るということなので、何か適当な状態を用意しておいて各々の演算子の固有空間への射影演算を次々に適用していけば良さそうです。具体的には、すべての物理量子ビットが$\ket{0}$になっている状態$\ket{00 \cdots 0}$に対して、

\ket{0}_{L} = \prod_{i=1}^{6} \frac{I+\bar{X_i}}{2} \prod_{j=1}^{6} \frac{I+\bar{Z_i}}{2} \frac{I+Z_{L}}{2} \ket{00 \cdots 0}  \tag{13}

という射影演算を実行すれば良いです⁶。ここで各射影演算は互いに可換、かつ、$Z$スタビライザーによる射影と$Z_{L}$演算は$\ket{00 \cdots 0}$を不変に保つので、式(13)は、

\ket{0}_{L} = \prod_{i=1}^{6} \frac{I+\bar{X_i}}{2} \ket{00 \cdots 0}  \tag{14}

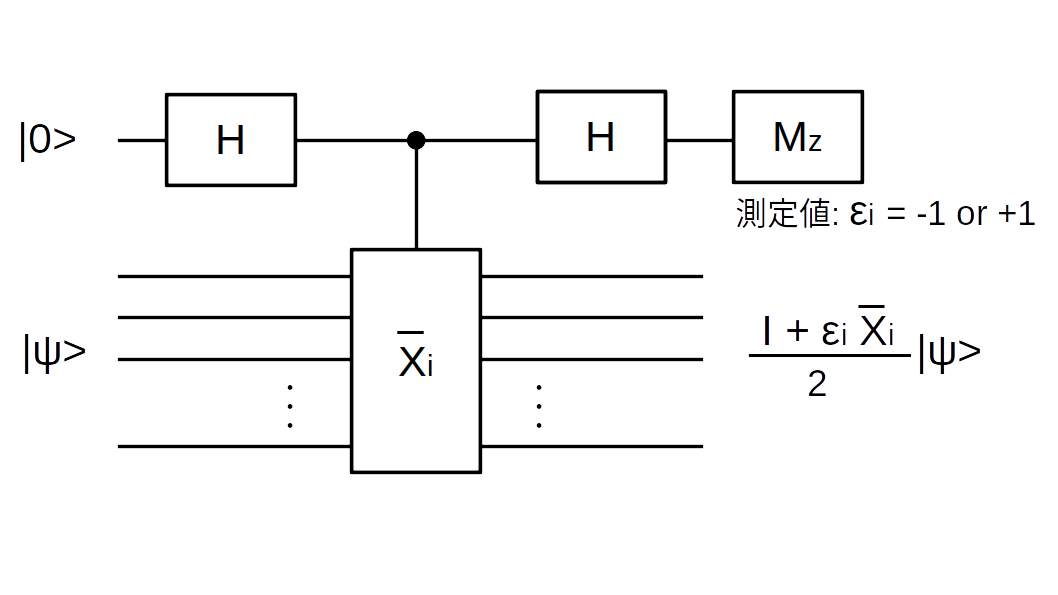
としても同じことです。数学的にはこれで終了なのですが、実際の量子回路で実行する際にはこの射影は測定操作になります。量子回路で書くと、

です。最後のアンシラの測定値が$+1$（$\ket{0}$）だった場合$\bar{X_i}$の固有値$+1$の固有状態に射影されますが、測定値が$-1$（$\ket{1}$）だった場合固有値$-1$の固有状態に射影されます。したがって、$\bar{X_i}$の測定値が$\epsilon_{i}$だったとすると、出来上がる状態は、

S_{0}^{\prime} = <\epsilon_{1} \bar{X_1}, \epsilon_{2} \bar{X_2}, \cdots, \epsilon_{6} \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \cdots, \bar{Z_6}, Z_{L}>  \tag{15}

となります。つまり、出来上がる$\ket{0}_{L}$の中身は確率的に変わるということになるのですが、各スタビライザーの測定値を覚えておけば後の論理演算をこのまま実行しても全然問題ないです（と思います）。気持ち悪い人は、測定値が$-1$になったら当該スタビライザーと反可換で他のスタビライザーと可換な演算子を演算することで固有値$-1$の固有状態を$+1$に反転させることができます。具体的には、以下のような演算子を演算すれば良いです。

そうすると、きれいな状態、

S_{0} = <\bar{X_1}, \bar{X_2}, \cdots, \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \cdots, \bar{Z_6}, Z_{L}>  \tag{16}

が得られます。が、現実的にはコヒーレンス時間は限られているので、このような反転演算を実際にやるのはよろしくないです。いずれにしろ、これで$\ket{0}_{L}$（式(15)または式(16)の形）が出来上がったことになります。$\ket{1}_{L}$はこの$\ket{0}_{L}$に$X_{L}$を演算すれば得られます。

では、$\ket{+}_{L}$を得たい場合はどうすれば良いでしょうか。後で説明する論理アダマール演算を使っても良いですが、初期化しておいてさらにアダマール演算というのはちょっと面倒です。上に類似した初期化プロセスのみで実現できた方がスマートです。どうやるかというと、最初にすべての量子ビットを$\ket{+}$に初期化しておいて、$Z$スタビライザーを順々に間接測定していきます。これで、

S_{+}^{\prime} = <\bar{X_1}, \bar{X_2}, \cdots, \bar{X_6}, \lambda_{1} \bar{Z_1}, \lambda_{2} \bar{Z_2}, \cdots, \lambda_{6} \bar{Z_6}, X_{L}>  \tag{17}

という状態$\ket{+}_{L}$が得られます。ここで$\lambda_{i}$は$\bar{Z_i}$の測定値です。先ほどのようにきれいな状態を得たい場合は、測定値が$-1$だった場合、そのスタビライザーとのみ反可換な演算子を演算すれば固有値を反転させることができます。結果、

S_{+} = <\bar{X_1}, \bar{X_2}, \cdots, \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \cdots, \bar{Z_6}, X_{L}>  \tag{18}

が得られます。$\ket{-}_{L}$が欲しい場合は$\ket{+}_{L}$に$Z_{L}$を演算すれば良いです。

マジック状態注入

$\ket{0}_{L}, \ket{1}_{L}, \ket{+}_{L}, \ket{-}_{L}$を作成する方法はわかりましたが、一般の論理状態、

\ket{\Psi}_{L} = \alpha \ket{0}_{L} + \beta \ket{1}_{L}  \tag{19}

を得たい場合があります。論理$T$演算子のような非クリフォード演算を実現する際にはある特定の状態（マジック状態）をアンシラとして用意しておく必要がありました。そんな場合、式(19)の状態を作りたくなるわけですが、それは、以下のようにすれば作れます。この操作のことをマジック状態注入（magic state injection）と呼びます。

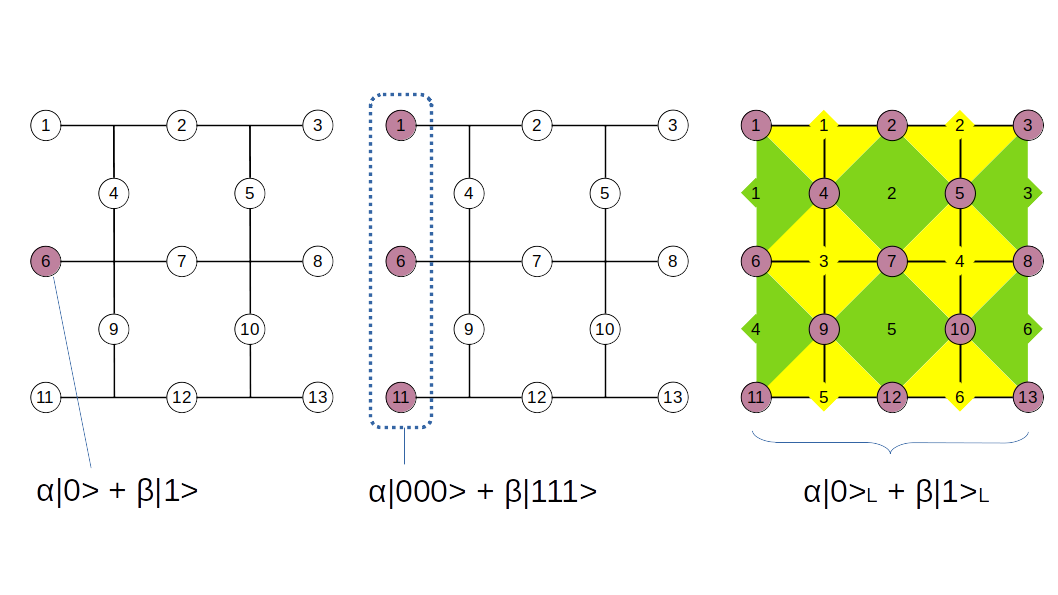
まず、上図左のように格子状に並んだ量子ビットを考えて、その左端中央の量子ビットを$\alpha \ket{0} + \beta \ket{1}$に初期化し、その他の量子ビットをすべて$\ket{0}$に初期化しておきます。次に、左端中央の量子ビット（6番）とその上の量子ビット（1番）に6番を制御ビットにしたCNOTを演算し、さらに左端中央とその下の量子ビット（11番）に6番を制御ビットにしたCNOTを演算します。そうすると、左端縦1列（上図中の紫色の量子ビット）の状態は、

\alpha \ket{000} + \beta \ket{111}  \tag{20}

になります（上図中）。さらに、$6$個ある$X$スタビライザーを順に間接測定していきます。これで、式(19)の論理状態が得られたことになります（上図右の紫色の量子ビット全体で式(18)の論理状態を構成します）⁷。

「得られたことになります」とサラッと言いましたが本当にそうなるのか、数式の上で確認してみます。

式(20)から出発することにします。すべての量子ビットに関してきちんと書くと、

\begin{align}
&(\alpha \ket{0}_{1} \ket{0}_{6} \ket{0}_{11} + \beta \ket{1}_{1} \ket{1}_{6} \ket{1}_{11}) \ket{0}_{2} \ket{0}_{3} \ket{0}_{4} \ket{0}_{5} \ket{0}_{7} \ket{0}_{8} \ket{0}_{9} \ket{0}_{10} \ket{0}_{12} \ket{0}_{13} \\
&= \alpha \ket{00 \cdots 0} + \beta X_{1} X_{6} X_{11} \ket{00 \cdots 0}  \tag{21}
\end{align}

です（下付きの添字は量子ビット番号を表します）。この状態に対して$X$スタビライザーを順に間接測定していきます。まず第1項について考えると、これは先ほどの初期化でやったように以下のような射影演算に相当します（測定によって確率的に射影後の結果が変わることを$\pm$で表わしています）。

\prod_{i=1}^{6} \frac{I \pm \bar{X_i}}{2} \alpha \ket{00 \cdots 0} = \alpha \ket{0}_{L}  \tag{22}

というわけで、これは$\ket{0}_{L}$の$\alpha$倍です。同様に第2項は、$X_{1} X_{6} X_{11}$が論理パウリ$X$演算子$X_L$だったことを思い出すと、

\prod_{i=1}^{6} \frac{I \pm \bar{X_i}}{2} \beta X_{1} X_{6} X_{11} \ket{00 \cdots 0} = \beta X_{L} \ket{0}_L = \beta \ket{1}_L \tag{23}

となり、これは$\ket{1}_L$の$\beta$倍です。式(22)と式(23)を合わせると、結局、

\alpha \ket{0}_{L} + \beta \ket{1}_{L}  \tag{24}

が得られたことになります。この方法の肝は最初に論理$X$演算子のチェーンに相当する量子ビットに対して式(20)のような状態を作成するということです。いまたまたま左端の1列の量子ビットに対して式(20)を作りましたが、真ん中もしくは右端のどっちかの縦1列で式(20)を作っておいても良いです。さらに大きな符号距離をもった論理状態を作りたい場合は、最初にサイズの大きな格子を用意しておいて上と同様の手続きを実行すれば良いです。が、一旦小さいサイズの格子で論理状態を作っておいて、後から格子サイズを拡張するやり方もありますので、次に詳しく見ていきます。

格子の拡張

まず、左右にrough boundary、上下にsmooth boundaryがある格子を横方向（つまりrough boundaryを横にずらす方向）に拡張することを考えます。

いま上図左の論理状態が、

\alpha \ket{0}_{L} + \beta \ket{1}_{L}  \tag{25}

だったとします。この格子に対して右側に隣接する形で量子ビットを追加します（上図右）。ただ追加しただけでは何も起きません。ある操作を加えることで、拡張された格子上でも

\alpha \ket{0}_{L}^{new} + \beta \ket{1}_{L}^{new}  \tag{26}

という状態にできます。横方向に増えたスタビライザーも含めた同時固有状態にしたいので、何となく新しいスタビライザーを間接測定すれば良さそうに思えます。例えば、新たに追加した量子ビットをすべて$\ket{0}$に初期化しておき、$X$スタビライザーを間接測定したらどうでしょうか（$Z$スタビライザーを間接測定しても何も起きないので無駄なことはしません）、という当たりをつけてやってみます。

式(25)の第1項の$\ket{0}_{L}$と第2項の$\ket{1}_{L}$に分けて考えます。まず、$\ket{0}_{L}$についてです。量子ビットを追加してすべて$\ket{0}$に初期化した直後の状態は、

<\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_6}, Z_L, Z_{14}, Z_{15}, Z_{16}, Z_{17}, Z_{18}>  \tag{27}

です。もとの$\bar{Z_3}$と$\bar{Z_6}$は3端子なのですが、横方向に増えたので各々$Z_{15}$と$Z_{17}$をかけて$\bar{Z_3} = Z_{3} Z_{5} Z_{15} Z_{8}, \space \bar{Z_6} = Z_{8} Z_{10} Z_{17} Z_{13}$という風に4端子にしておきます。また、$Z_L$は$Z_{14}$をかけて$Z_{L}^{new} = Z_{1} Z_{2} Z_{3} Z_{14}$としておきます。そうすると、式(27)は、

<\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_6}, Z_{L}^{new}, Z_{14}, Z_{15}, Z_{16}, Z_{17}, Z_{18}>  \tag{28}

となります。さらに、5つの孤立した$Z_{14}, Z_{15}, Z_{16}, Z_{17}, Z_{18}$たちを適当に掛け合わせて、3端子の$Z$スタビライザーを2つひねり出します。

\begin{align}
&<\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_6}, Z_{L}^{new}, Z_{14} Z_{15} Z_{16}, Z_{16} Z_{17} Z_{18}, Z_{14}, Z_{16}, Z_{18}>  \\
&= <\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_6}, Z_{L}^{new}, \bar{Z_7}, \bar{Z_8}, Z_{14}, Z_{16}, Z_{18}>  \\
&= <\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_8}, Z_{L}^{new}, Z_{14}, Z_{16}, Z_{18}>  \tag{29}
\end{align}

こう変形しておいてから、おもむろに$X$スタビライザーを測定します。まず、$X_{3} X_{14} X_{15} = \bar{X_7}$を測定します。これに反可換なものは$Z_{14}$しかありません。測定値は$+1$か$-1$になるのですが、それを$\epsilon_{7}$と書くことにすると、

<\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_8}, Z_{L}^{new}, \epsilon_{7} \bar{X_7}, Z_{16}, Z_{18}>  \tag{30}

となります。同じように、$X_{15} X_{8} X_{16} X_{17} = \bar{X_8}$および$X_{17} X_{13} X_{18} = \bar{X_9}$を測定すると、

\begin{align}
&<\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_8}, Z_{L}^{new}, \epsilon_{7} \bar{X_7}, \epsilon_{8} \bar{X_8}, \epsilon_{9} \bar{X_9}> \\
&= <\bar{X_1}, \cdots ,\bar{X_6}, \epsilon_{7} \bar{X_7}, \epsilon_{8} \bar{X_8}, \epsilon_{9} \bar{X_9}, \bar{Z_1}, \cdots ,\bar{Z_8}, Z_{L}^{new}>  \tag{31}
\end{align}

となります。したがって、新しい論理パウリ$Z$演算子$Z_{L}^{new}$の固有値$+1$に対する固有状態になることがわかります。この状態を$\ket{0}_{L}^{new}$と定義しておきます。

もう一方の$\ket{1}_{L}$については式(27)の$Z_{L}$の符号をマイナスになったものから出発します。量子ビットを追加してすべて$\ket{0}$に初期化した直後の状態は、

<\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_6}, -Z_L, Z_{14}, Z_{15}, Z_{16}, Z_{17}, Z_{18}>  \tag{32}

となっており、上と同じ式展開により、

<\bar{X_1}, \cdots ,\bar{X_6}, \epsilon_{7} \bar{X_7}, \epsilon_{8} \bar{X_8}, \epsilon_{9} \bar{X_9}, \bar{Z_1}, \cdots ,\bar{Z_8}, -Z_{L}^{new}>  \tag{33}

となるので、これは新しい論理パウリ$Z$演算子$Z_{L}^{new}$の固有値$-1$に対する固有状態です。この状態を$\ket{1_L}^{new}$と定義します⁸。

結局、このような横方向の拡張によって、

\alpha \ket{0}_{L} + \beta \ket{1}_{L} \Rightarrow \alpha \ket{0}_{L}^{new} + \beta \ket{1}_{L}^{new}  \tag{34}

ができたことになります。

次に、縦方向（つまりsmooth boundaryを下にずらす方向）に拡張することを考えます。これは、$X$スタビライザーと$Z$スタビライザーの立場をまるごと入れ替えると、まさに横方向の拡張で考えたことと全く同じになります。というわけで、下方向に用意した量子ビットを$\ket{0}$ではなく$\ket{+}$に初期化しておき、$X$スタビライザーではなく$Z$スタビライザーを測定すれば良いということになります。

上図左の論理状態が、

\alpha \ket{0}_{L} + \beta \ket{1}_{L} = \alpha^{\prime} \ket{+}_{L} + \beta^{\prime} \ket{-}_{L}  \tag{35}

\begin{align}
\alpha^{\prime} &= \frac{1}{\sqrt{2}} (\alpha + \beta) \\ 
\beta^{\prime} &= \frac{1}{\sqrt{2}} (\alpha - \beta)  \tag{36} 
\end{align}

だったとします。この格子に対して下側に隣接する形で量子ビットを追加してすべて$\ket{+}$に初期化しておきます（上右図）。

$\ket{+}_{L}$に関して、量子ビットを追加して初期化した直後の状態は、

<\bar{X_1}, \cdots ,\bar{X_6}, \bar{Z_1}, \cdots ,\bar{Z_6}, X_L, X_{14}, X_{15}, X_{16}, X_{17}, X_{18}>  \tag{37}

です。先ほどと同様に伸ばしたい境界に位置する3端子のスタビライザー（$X$スタビライザー）を4端子にして、$X_L = X_{1} X_{6} X_{11}$を新しい$X_{L}^{new} = X_{1} X_{6} X_{11} X_{16}$に変えて、さらに6個の$Z$スタビライザーを順に測定していくと、

<\bar{X_1}, \cdots ,\bar{X_8}, \bar{Z_1}, \cdots ,\bar{Z_6}, \lambda_{7} \bar{Z_7}, \lambda_{8} \bar{Z_8}, \lambda_{9} \bar{Z_9}, X_{L}^{new}>  \tag{38}

となります。ここで$Z$スタビライザー$Z_{i}$の測定値を$\lambda_{i}$と置きました。これは新しい論理パウリ$X$演算子$X_{L}^{new}$の固有値$+1$に対する固有状態です（$\ket{+}_{L}^{new}$と定義します）。

一方、$\ket{-}_{L}$に関して、同様に6個の$Z$スタビライザーを順に測定すると、

<\bar{X_1}, \cdots ,\bar{X_8}, \bar{Z_1}, \cdots ,\bar{Z_6}, \lambda_{7} \bar{Z_7}, \lambda_{8} \bar{Z_8}, \lambda_{9} \bar{Z_9}, -X_{L}^{new}>  \tag{39}

となります。これは新しい論理パウリ$X$演算子$X_{L}^{new}$の固有値$-1$に対する固有状態です（$\ket{-}_{L}^{new}$と定義します）⁹。

結局、このような縦方向の拡張によって、

\begin{align}
&\alpha \ket{0_L} + \beta \ket{1_L} = \alpha^{\prime} \ket{+_{L}} + \beta^{\prime} \ket{-_{L}}  \\
&\Rightarrow \alpha^{\prime} \ket{+}_{L}^{new} + \beta^{\prime} \ket{-}_{L}^{new} = \alpha \ket{0_L}^{new} + \beta \ket{1_L}^{new}  \tag{40}
\end{align}

ができたことになります¹⁰。

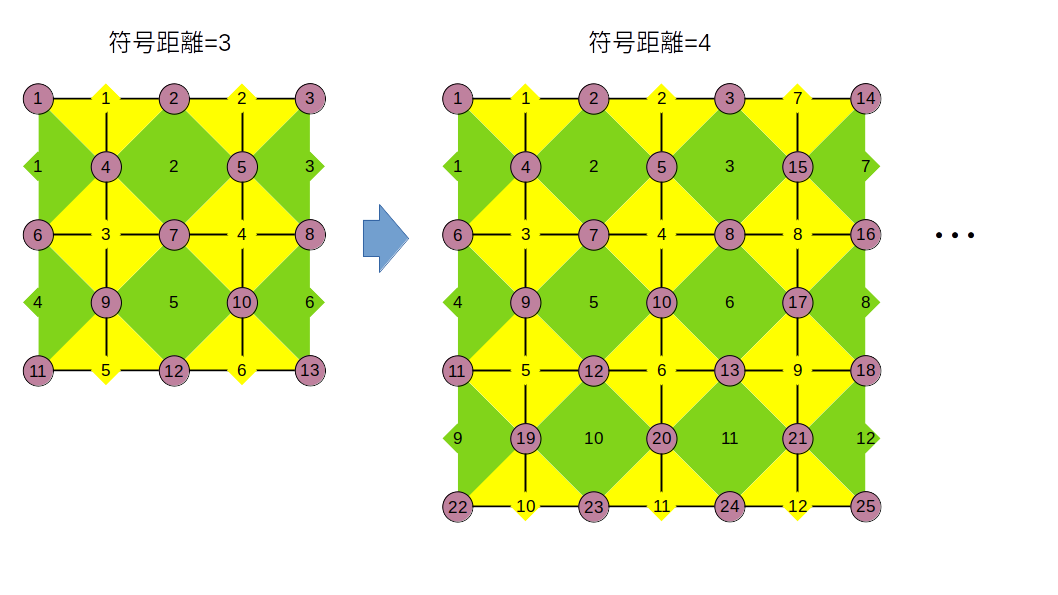
この横方向と縦方向の拡張を繰り返し実行することで、下図に示したように任意の符号距離の論理状態を作成することができます。

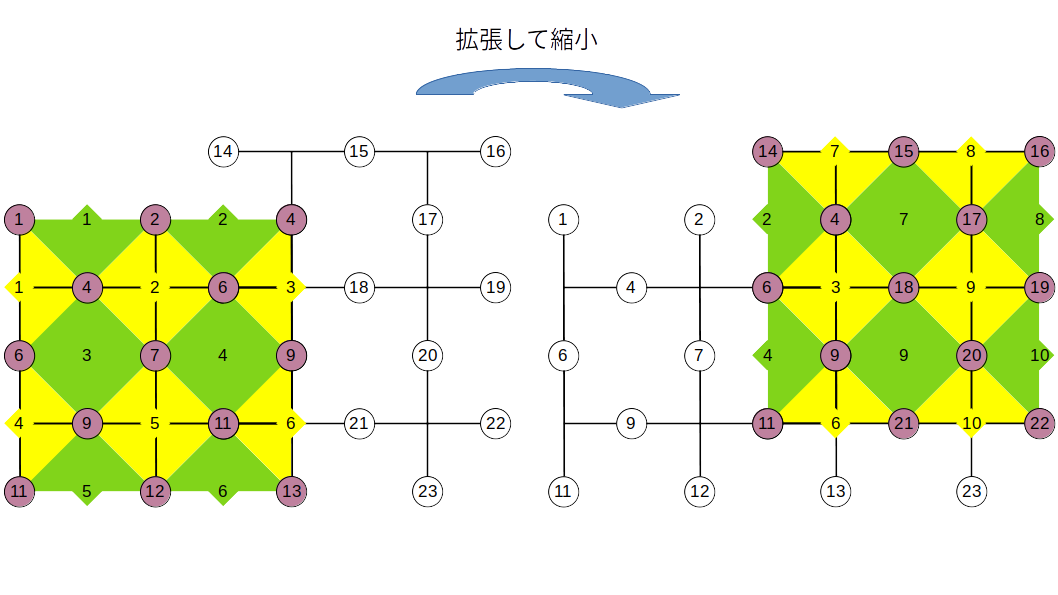
格子の縮小

では、逆に格子を縮小するにはどうすれば良いでしょうか。

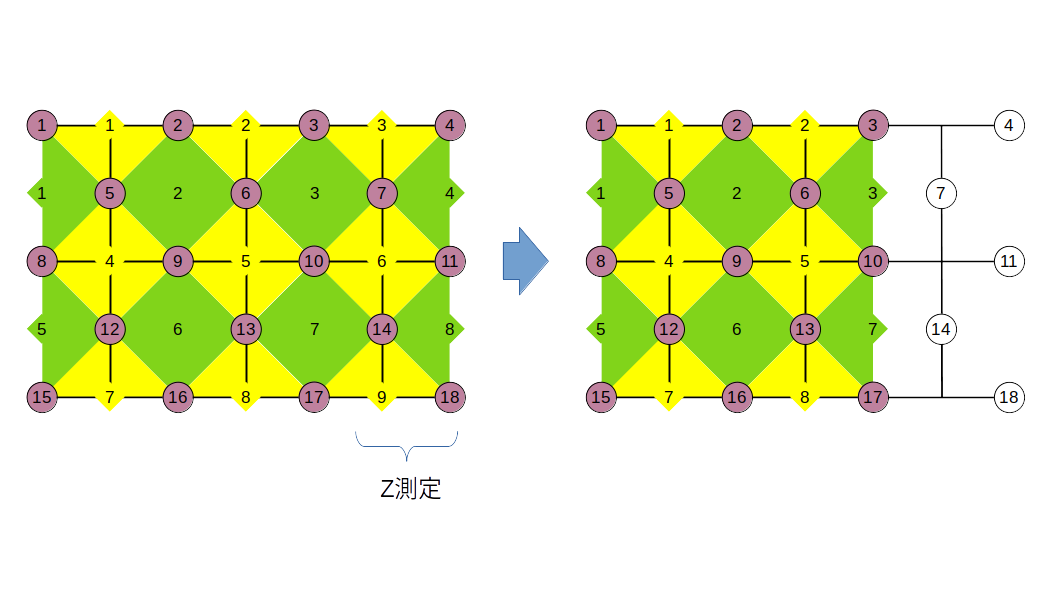
横方向の縮小は横方向の拡張の逆をイメージすれば良いです。つまり、左の端にある量子ビットを$Z$測定して$\ket{0}$（または$\ket{1}$）に戻します（下図）。

本当にこれで良いのか数式の上で確認してみます。上図左の格子が$\alpha \ket{0}_{L} + \beta \ket{1}_{L}$を表しているとして$\ket{0}_{L}$と$\ket{1}_{L}$が各々縮小操作でどう変化するかを考えます。まず、$\ket{0}_{L}$はスタビライザー形式で書くと、

<\bar{X_1}, \cdots ,\bar{X_9}, \bar{Z_1}, \cdots ,\bar{Z_8}, Z_L>  \tag{41}

です。ここで、$Z_L = Z_{1} Z_{2} Z_{3} Z_{4}$としておきます。まず1番右の$Z_{4}, Z_{11}, Z_{18}$を測定します。反可換な演算子は各々$\bar{X_3}, \bar{X_6}, \bar{X_9}$です。その測定値を各々$\mu_{4}, \mu_{11}, \mu_{18}$とすると、測定後の状態は、

<\bar{X_1}, \bar{X_2}, \bar{X_4}, \bar{X_5}, \bar{X_7}, \bar{X_8}, \mu_{4} Z_{4}, \mu_{11} Z_{11}, \mu_{18} Z_{18}, \bar{Z_1}, \cdots ,\bar{Z_8}, Z_L>  \tag{42}

となります。また、3端子の2つの$Z$スタビライザー$\bar{Z_4}, \bar{Z_8}$に$\mu_{4} Z_{4}, \mu_{11} Z_{11}, \mu_{18} Z_{18}$を適当に選んでかけると、

<\bar{X_1}, \bar{X_2}, \bar{X_4}, \bar{X_5}, \bar{X_7}, \bar{X_8}, \mu_{4} Z_{4}, \mu_{11} Z_{11}, \mu_{18} Z_{18}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \mu_{4} \mu_{11} Z_{7}, \mu_{11} \mu_{18} Z_{14}, Z_L>  \tag{43}

のように単体の$Z$演算子に変えることができます。さらに、4端子の$\bar{Z_3},\bar{Z_7}$に各々$\mu_{4} \mu_{11} Z_{7}, \mu_{11} \mu_{18} Z_{14}$をかけて3端子にして、論理パウリ$Z$演算子に$\mu_{4} Z_{4}$をかけて$Z_{L}^{new} = \mu_{4} Z_{1} Z_{2} Z_{3}$を定義すると、

<\bar{X_1}, \bar{X_2}, \bar{X_4}, \bar{X_5}, \bar{X_7}, \bar{X_8}, \mu_{4} Z_{4}, \mu_{11} Z_{11}, \mu_{18} Z_{18}, \bar{Z_1}, \bar{Z_2}, \mu_{4} \mu_{11} \bar{Z_3}, \bar{Z_5}, \bar{Z_6}, \mu_{11} \mu_{18} \bar{Z_7}, \mu_{4} \mu_{11} Z_{7}, \mu_{11} \mu_{18} Z_{14}, Z_{L}^{new}>  \tag{44}

となります。整理すると、

<\bar{X_1}, \bar{X_2}, \bar{X_4}, \bar{X_5}, \bar{X_7}, \bar{X_8}, \bar{Z_1}, \bar{Z_2}, \mu_{4} \mu_{11} \bar{Z_3}, \bar{Z_5}, \bar{Z_6}, \mu_{11} \mu_{18} \bar{Z_7}, Z_{L}^{new}> \otimes <\mu_{4} Z_{4}, \mu_{4} \mu_{11} Z_{7}, \mu_{11} Z_{11}, \mu_{11} \mu_{18} Z_{14}, \mu_{18} Z_{18}>  \tag{45}

となり、後半を無視して、

<\bar{X_1}, \bar{X_2}, \bar{X_4}, \bar{X_5}, \bar{X_7}, \bar{X_8}, \bar{Z_1}, \bar{Z_2}, \mu_{4} \mu_{11} \bar{Z_3}, \bar{Z_5}, \bar{Z_6}, \mu_{11} \mu_{18} \bar{Z_7}, Z_{L}^{new}>  \tag{46}

とすれば所望の縮小された論理状態を得ることができます。ここで、注意しておきたいことが一つあります。式(46)に含まれる新しい論理パウリ$Z$演算子は、

Z_{L}^{new} = \mu_{4} Z_{1} Z_{2} Z_{3}  \tag{47}

になっています。つまり、$Z_{4}$の測定値が$-1$だった場合、$Z_{1} Z_{2} Z_{3}$の固有値$-1$の固有状態になりますので、縮小したら論理演算子のチェーンも単純に短くなるのである、と考えていると痛い目を見ます。測定値に応じて論理パウリ$Z$演算子の符号が反転するのでそれを考慮して後の測定結果を解釈する必要があります¹¹。

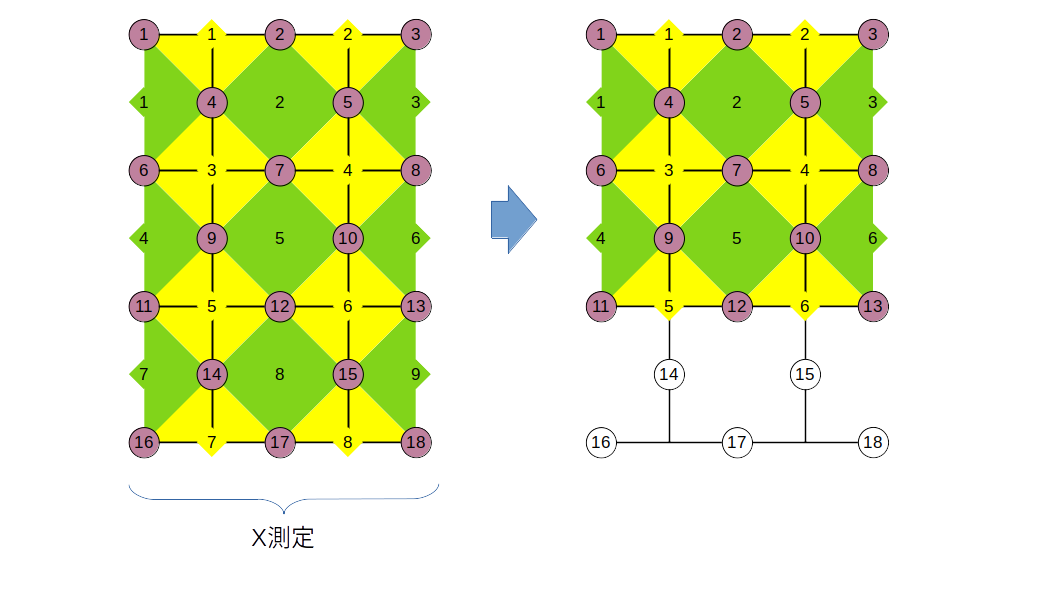
次に、縦方向の縮小について考えます。横方向の縮小で$X$と$Z$の立場を入れ替えて考えれば良いです。つまり、下端の量子ビットを$X$測定して$\ket{+}$（または$\ket{-}$）に戻します。

一応、数式の上で確認してみます。上図左の格子が、

\alpha \ket{0}_{L} + \beta \ket{1}_{L} = \alpha^{\prime} \ket{+}_{L} + \beta^{\prime} \ket{-}_{L}  \tag{48}

を表しているとして$\ket{+}_{L}$と$\ket{-}_{L}$が各々縮小操作でどう変化するかを考えます。まず、$\ket{+}_{L}$についてです。最初の状態は、

<\bar{X_1}, \cdots ,\bar{X_9}, \bar{Z_1}, \cdots ,\bar{Z_8}, X_L>  \tag{49}

です。ここで、$X_L = X_{1} X_{6} X_{11} X_{16}$としておきます。下端の$X_{14}, X_{15}, X_{16}, X_{17}, X_{18}$を測定しますが、そのときの測定値を各々$\nu_{14}, \nu_{15}, \nu_{16}, \nu_{17}, \nu_{18}$とすると、

<\bar{X_1}, \bar{X_2}, \bar{X_3}, \bar{X_4}, \nu_{16} \nu_{17} \bar{X_5}, \nu_{17} \nu_{18} \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, X_{L}> \otimes <\nu_{16} \nu_{17} X_{14}, \nu_{17} \nu_{18} X_{15}, \nu_{16} X_{16}, \nu_{17} X_{17}, \nu_{18} X_{18}>  \tag{50}

となり、後半を無視して、

<\bar{X_1}, \bar{X_2}, \bar{X_3}, \bar{X_4}, \nu_{16} \nu_{17} \bar{X_5}, \nu_{17} \nu_{18} \bar{X_6}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}>  \tag{51}

とすれば所望の縮小された論理状態を得ることができます。先ほどと同様、ここで、注意しておきたいことが一つあります。式(51)に含まれる新しい論理パウリ$X$演算子は、

X_{L}^{new} = \nu_{16} X_{1} X_{6} Z_{11}  \tag{52}

です。測定値に応じて論理パウリ$X$演算子の符号が反転するのでそれを考慮して後の測定結果を解釈する必要があります¹²。

論理アダマール演算

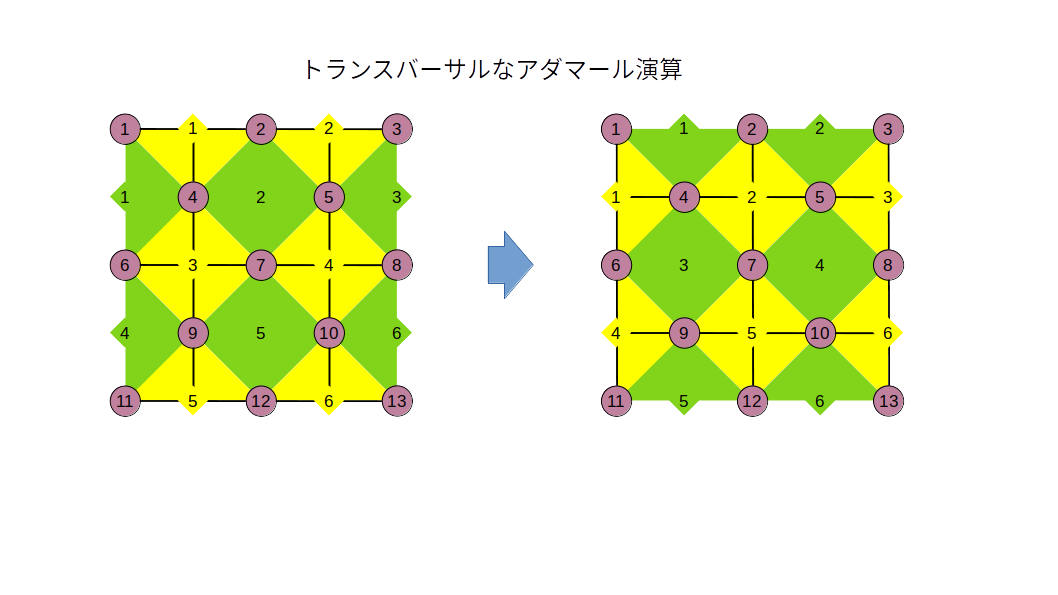
次に、論理アダマール演算について説明します。一番簡単なのは各物理量子ビットすべてに対してトランスバーサルにアダマール演算を実行する方法です。以前、フォールトトレラント量子計算を勉強した際には、これでOKとしていました。が、表面符号を前提にすると一つ困ったことが起きます。例えば、式(5)に立ち戻って考えてみてください。これは$\ket{0}_{L}$を表していますが、アダマール演算によって$Z_L$が$X_L$に変わります。つまり、$\ket{+}_{L}$に変わるということなので、確かに論理的なアダマール演算ができているのですが、同時に$X$スタビライザーが$Z$スタビライザーに変わり、$Z$スタビライザーが$X$スタビライザーに変わります。図で表すと以下のようになって、ちょうどもとの格子が90度回転したような格好になります。

これは非常にまずいです。$X$スタビライザーで誤り検出するべきところを$Z$スタビライザーで誤り検出をしてしまうことになるので、これでは誤り訂正になりません。かと言って、格子を物理的に90度回すというのも非現実的です。じゃあ、どうするか。格子サイズの拡張とスワップを使って、90度回転を模した操作を実現すれば良いです。

上図左に示した90度回転してしまった格子を出発点にします。これに対して上図右に示すように量子ビットを右上方向に拡張し、紫色で示した量子ビットだけを残すように縮小します。そうすると紫色で示した部分は元と同じ向きの格子になっています。完全に元の格子の位置に戻したい場合は、さらに適当にスワップ演算をすれば戻ります。以上です。どうでしょう。ちょっと面倒ですか？でも、Braidingで論理アダマール演算をやったときと比べるとはるかに簡単だと思います。

論理2量子ビット演算

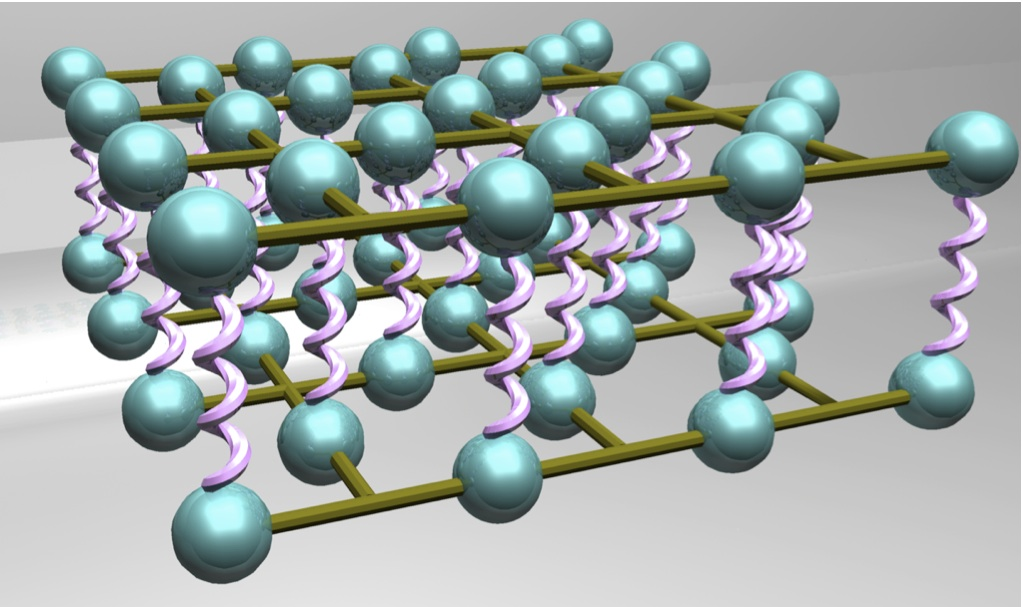
論理1量子ビット演算はこれで一通り実現できたということになるので（非クリフォード演算はマジック状態注入とテレポーテーションでできたことにして）、次に、論理2量子ビット演算の代表選手として論理CNOT演算について考えてみます。とにかく、トランスバーサルにCNOT演算を実行するということなので、平面符号では以下のようにやるしかないです（参考文献1のきれいな絵を掲載します）。

上図でバネのようにぐるぐる回っているものがCNOT演算の制御と標的のつながりを表しています。このように3次元的に物理量子ビットを積み上げないとうまくいかないです。というわけで、平面符号で2量子ビット演算を実現するためには、ハードウエアにかなり無理難題を押し付けないと到底実現できそうにありません¹³。

というわけで、お待たせしました！Lattice Surgeryの出番です！

"Lattice"を"Surgery"するように、切ったり（Lattice splitting）くっつけたり（Lattice merging）することで、なんとCNOT演算ができてしまうのです。もう、量子ビットを3次元的に立体構成することに頭を悩ます必要はありません！

Lattice Surgery

と威勢よく言いましたが、論理CNOTを実現するためには、まずLattice Surgeryにおける基本操作であるmergeとsplitについて理解しておく必要がありますので、その説明から入ります。

Lattice merging

平面符号で表した2つの論理量子ビットを1つの論理量子ビットに合体させる操作のことをlattice mergingと呼びます。特に、rough boundary同士を合わせる操作をrough mergeと呼び、smooth boundary同士を合わせる操作をsmooth mergeと呼びます。

まず、rough mergeについてです。下図上に示すように、左と右の論理状態が各々、

\begin{align}
\ket{\psi} &= \alpha \ket{0}_{L} + \beta \ket{1}_{L} \\
\ket{\phi} &= \alpha^{\prime} \ket{0}_{L} + \beta^{\prime} \ket{1}_{L}  \tag{53}
\end{align}

だったとします。rough mergeは左右のrough boundaryの間にある量子ビットを$\ket{0}$に初期化してそれを含む$X$スタビライザーを間接測定することで全体を1個のエンタングルした論理状態にする操作です。

最初は並んだだけの状態なので、

\begin{align}
\ket{\psi} \ket{\phi} &= (\alpha \ket{0}_{L} + \beta \ket{1}_{L}) (\alpha^{\prime} \ket{0}_{L} + \beta^{\prime} \ket{1}_{L})  \\
&= \alpha \alpha^{\prime} \ket{0}_{L} \ket{0}_{L} + \alpha \beta^{\prime} \ket{0}_{L} \ket{1}_{L} + \beta \alpha^{\prime} \ket{1}_{L} \ket{0}_{L} + \alpha^{\prime} \beta^{\prime} \ket{1}_{L} \ket{1}_{L}  \tag{54}
\end{align}

です。これがmerge操作でどう変化するか計算してみます。上式の各項を別々に考えます。まず、$\ket{0}_{L} \ket{0}_{L}$です（以下、$\ket{00}_{L}$と簡略化して表します）。間にある量子ビットを$\ket{0}$にした直後の状態をスタビライザー形式で書くと、

\ket{00}_{L} = <\bar{X_1}, \bar{X_2}, \bar{X_6}, \bar{X_7}, \bar{X_{11}}, \bar{X_{12}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, Z_L, \bar{X_4}, \bar{X_5}, \bar{X_9}, \bar{X_{10}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{L}^{\prime}, Z_{9}, Z_{20}>  \tag{55}

ここで、$Z_L = Z_{1} Z_{2} Z_{3}, \space Z_{L}^{\prime} = Z_{4} Z_{5} Z_{6}$とします。また、つなげようとしている境界付近に3端子の$Z$スタビライザーが4つ（$= \bar{Z_3}, \bar{Z_4}, \bar{Z_9}, \bar{Z_{10}}$）あるのが気持ち悪いので、各々$Z_9$と$Z_{10}$をかけて4端子にしておきます（式(55)はそうした後の状態だと思ってください）。

この状態に対して、$\bar{X_3}$を間接測定します。$\bar{X_3}$と反可換な演算子は$Z_9, \space Z_L = Z_{1} Z_{2} Z_{3}, \space Z_{L}^{\prime} = Z_{4} Z_{5} Z_{6}$の3つなので、$Z_9$を$Z_L = Z_{1} Z_{2} Z_{3}, \space Z_{L}^{\prime} = Z_{4} Z_{5} Z_{6}$にかけて、反可換なものを$Z_9$だけにして$\bar{X_3}$を測定します。測定値が$\epsilon_{3}$だったとすると、

\rightarrow <\bar{X_1}, \bar{X_2}, \epsilon_{3} \bar{X_3}, \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \bar{X_9}, \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{1} Z_{2} Z_{3} Z_{9}, Z_{4} Z_{5} Z_{6} Z_{9}, Z_{20}>  \tag{56}

となります。同様に$\bar{X_8}$を測定し測定値が$\epsilon_{8}$だったとすると、

\rightarrow <\bar{X_1}, \bar{X_2}, \epsilon_{3} \bar{X_3}, \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \epsilon_{8} \bar{X_8},\bar{X_9}, \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{1} Z_{2} Z_{3} Z_{9} Z_{20}, Z_{4} Z_{5} Z_{6} Z_{9} Z_{20}>  \tag{57}

となり、$\bar{X_{13}}$を測定し測定値が$\epsilon_{13}$だったとすると、

\begin{align}

&\rightarrow <\bar{X_1}, \bar{X_2}, \epsilon_{3} \bar{X_3}, \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \epsilon_{8} \bar{X_8}, \bar{X_9}, \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \epsilon_{13} \bar{X_{13}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{1} Z_{2} Z_{3} Z_{4} Z_{5} Z_{6}>  \\

&= <\bar{X_1}, \bar{X_2}, \epsilon_{3} \bar{X_3}, \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \epsilon_{8} \bar{X_8}, \bar{X_9}, \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \epsilon_{13} \bar{X_{13}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{L} Z_{L}^{\prime}> \tag{58}

\end{align}

となります。これはさらに、

\begin{align}

&= <\bar{X_1}, \bar{X_2}, \epsilon_{3} \bar{X_3}, \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \epsilon_{8} \bar{X_8}, \bar{X_9}, \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \epsilon_{13} \bar{X_{13}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{L} Z_{L}^{\prime}>  \\

&= <\bar{X_1}, \bar{X_2}, \epsilon_{3} \epsilon_{8} \epsilon_{13} \bar{X_3} \bar{X_8} \bar{X_{13}}, \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \epsilon_{8} \bar{X_8}, \bar{X_9}, \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \epsilon_{13} \bar{X_{13}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{L} Z_{L}^{\prime}>  \\

&= <\bar{X_1}, \bar{X_2}, \epsilon_{3} \epsilon_{8} \epsilon_{13} X_{3} X_{14} X_{25} \dot X_{4} X_{15} X_{26}, \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \epsilon_{8} \bar{X_8}, \bar{X_9}, \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \epsilon_{13} \bar{X_{13}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{L} Z_{L}^{\prime}>  \\

&= <\bar{X_1}, \bar{X_2}, \epsilon_{3} \epsilon_{8} \epsilon_{13} X_{L} X_{L}^{\prime}, \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \epsilon_{8} \bar{X_8}, \bar{X_9}, \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \epsilon_{13} \bar{X_{13}}, \bar{X_{14}}, \bar{X_{15}}, \bar{Z_1}, \bar{Z_2}, \bar{Z_3}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, \bar{Z_8}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{L} Z_{L}^{\prime}>  \tag{59}

\end{align}

のように変形できます。ここで、$X_{L},\space X_{L}^{\prime}$は各々元の論理ビットに対する2つの論理パウリ$X$演算子であり、$X_{L} = X_{3} X_{14} X_{25}, \space X_{L}^{\prime} = X_{4} X_{15} X_{26}$としました。ごちゃごちゃしてわかりにくいので、4端子と3端子スタビライザーを点々で表し論理パウリ演算子みたいな顔をしているところだけ目立たせると、結局この操作で、

\ket{00}_{L} \rightarrow <\cdots, \epsilon_{3} \epsilon_{8} \epsilon_{13} X_{L} X_{L}^{\prime}, \cdots, Z_{L} Z_{L}^{\prime}>  \tag{60}

のように変化したことになります。$\epsilon_{i} = (-1)^{m_i}$のように$m_{i}$を定義して$M = m_{3} \oplus m_{8} \oplus m_{13}$とおくと、式(59)は、

\ket{00}_{L} \rightarrow <\cdots, (-1)^{M} X_{L} X_{L}^{\prime}, \cdots, Z_{L} Z_{L}^{\prime}>  \tag{61}

のように書けます。同じことを$\ket{01}_{L}, \ket{10}_{L}, \ket{11}_{L}$に対しても行うと、各々、

\begin{align}
\ket{01}_{L} &\rightarrow <\cdots, (-1)^{M} X_{L} X_{L}^{\prime}, \cdots, -Z_{L} Z_{L}^{\prime}>  \\
\ket{10}_{L} &\rightarrow <\cdots, (-1)^{M} X_{L} X_{L}^{\prime}, \cdots, -Z_{L} Z_{L}^{\prime}>  \\
\ket{11}_{L} &\rightarrow <\cdots, (-1)^{M} X_{L} X_{L}^{\prime}, \cdots, Z_{L} Z_{L}^{\prime}>  \tag{62}
\end{align}

のように変化します。式(60)と式(61)をよーく眺めてみてください。$\ket{00}_{L}$と$\ket{11}_{L}$（およびその線形結合）は$Z_{L} Z_{L}^{\prime}$の固有値$+1$の固有状態にマッピングされ、$\ket{01}_{L}$と$\ket{10}_{L}$（およびその線形結合）は$Z_{L} Z_{L}^{\prime}$の固有値$-1$の固有状態にマッピングされることがわかります。つまり、もとの論理的2量子ビット状態=4次元ヒルベルト空間（2次元と2次元の直積）が、merge操作によって論理的1量子ビット状態=2次元ヒルベルト空間にちゃんとマッピングされました、ということがわかります。さらに、これが重要なことなのですが、もとの4つの基底がすべて$X_{L} X_{L}^{\prime}$の固有値$(-1)^{M}$の固有空間にマッピングされているということです。つまり、このmerge操作というのは、もとの$\ket{\psi} \otimes \ket{0}_{9} \ket{0}_{20} \otimes \ket{\phi}$に対して$X_{L} X_{L}^{\prime}$という演算子（上図で青いチェーンで示した演算子$X_{3} X_{14} X_{25} X_{26} X_{15} X_{4}$）を間接測定して¹⁴測定値が$(-1)^{M}$だった」ということと等価だと解釈しても良いということです。

すなわち、merge操作というのは、

\ket{\psi} \ket{\phi} \rightarrow \ket{\psi} \odot \ket{\phi} = (I + (-1)^{M} X_{L} X_{L}^{\prime}) \ket{\psi} \ket{\phi}  \tag{63}

という演算に他なりません。ここで、$\odot$をmerge操作を表す演算と定義し¹⁵、規格化定数は省略しました（以降同様に規格化定数は省略します）。$\ket{\psi}$と$\ket{\phi}$の間に本当は$\ket{0}_{9} \ket{0}_{20}$が存在しているのですが省略しました¹⁶。

式(63)の右辺を式(53)を使って展開すると、$M=0$の場合は、

\ket{\psi} \odot \ket{\phi} = (\alpha \alpha^{\prime} + \beta \beta^{\prime}) (\ket{00}_{L} + \ket{11}_{L}) + (\alpha \beta^{\prime} + \beta \alpha^{\prime}) (\ket{01}_{L} + \ket{10}_{L})    \tag{64}

となり、$M=1$の場合は、

\ket{\psi} \odot \ket{\phi} = (\alpha \alpha^{\prime} - \beta \beta^{\prime}) (\ket{00}_{L} - \ket{11}_{L}) + (\alpha \beta^{\prime} - \beta \alpha^{\prime}) (\ket{01}_{L} - \ket{10}_{L})    \tag{65}

となります。$M$の値に応じて、merge後の基底を、

\begin{align}
\ket{00} + (-1)^{M} \ket{11} &\rightarrow \ket{0}_{L} \\
\ket{01} + (-1)^{M} \ket{10} &\rightarrow \ket{1}_{L} \tag{66}
\end{align}

のように定めると、式(64)(65)は、

\begin{align}
\ket{\psi} \odot \ket{\phi} &= (\alpha \alpha^{\prime} + (-1)^{M} \beta \beta^{\prime}) (\ket{00}_{L} + (-1)^{M} \ket{11}_{L}) + (\alpha \beta^{\prime} + (-1)^{M} \beta \alpha^{\prime}) (\ket{01}_{L} + (-1)^{M} \ket{10}_{L})   \\
&= \alpha (\alpha^{\prime} \ket{0}_{L} + \beta^{\prime} \ket{1}_{L}) + (-1)^{M} \beta (\alpha^{\prime} \ket{1}_{L} + \beta^{\prime} \ket{0}_{L})  \\
&= \alpha \ket{\phi} + (-1)^{M} X_{L}^{\prime} \ket{\phi}  \tag{67}
\end{align}

のようにまとめることができます。これがrough mergeの基本公式です。後で使いますので覚えておきましょう。

次に、smooth mergeについて考えてみます。下図に示すように、左と右の論理状態が各々、

\begin{align}
\ket{\psi} &= a \ket{+}_{L} + b \ket{-}_{L} \\
\ket{\phi} &= a^{\prime} \ket{+}_{L} + b^{\prime} \ket{-}_{L}  \tag{68}
\end{align}

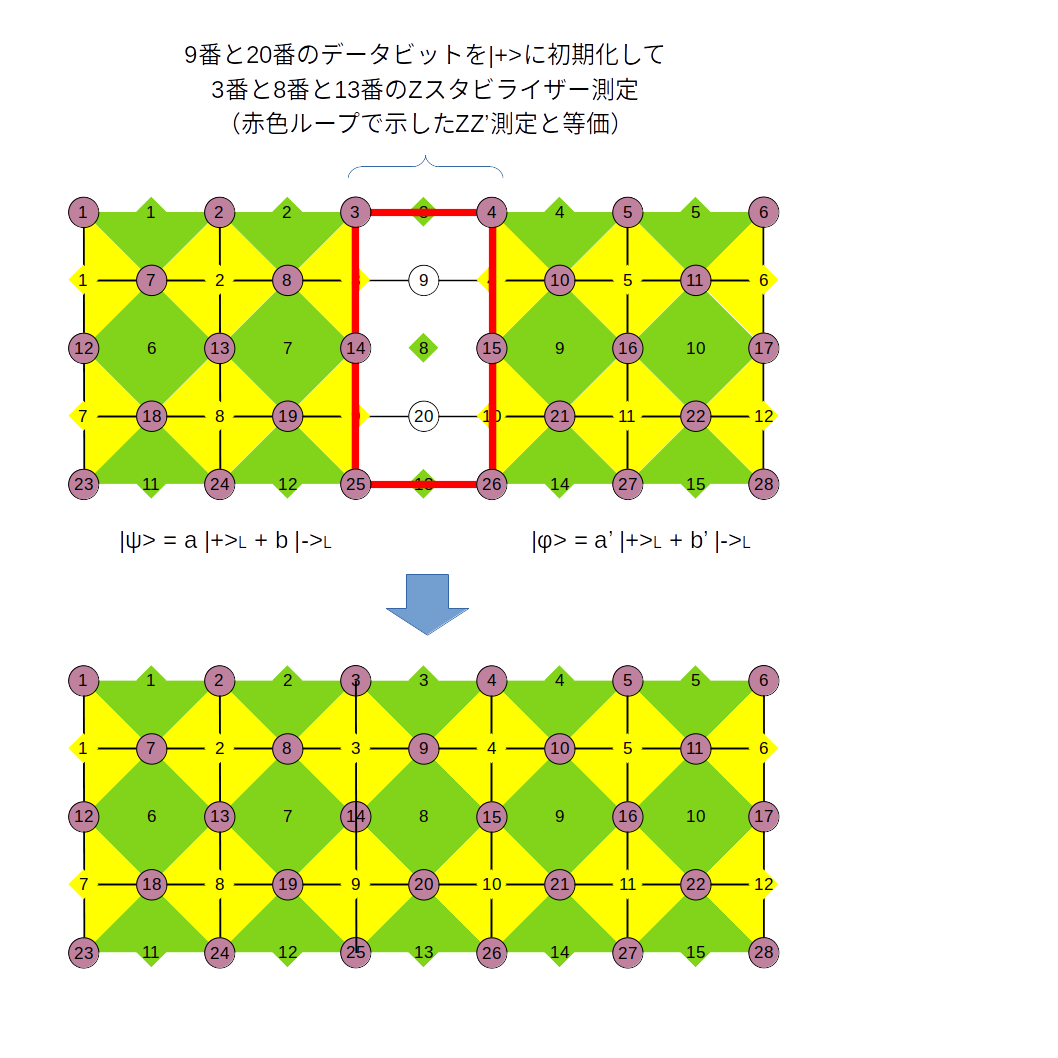
だったとします。smooth mergeは左右のsmooth boundaryの間にある量子ビットを$\ket{+}$に初期化してそれを含む$Z$スタビライザーを間接測定することで全体を1個のエンタングルした論理状態にする操作です。

rough mergeの$X$と$Z$の立場を入れ替えれば、先ほどとまったく同じ式展開ができます。smooth merge後の基底を測定値に応じて、

\begin{align}
\ket{++}_{L} + (-1)^{M} \ket{--}_{L} &\rightarrow \ket{+}_{L}  \\
\ket{+-}_{L} + (-1)^{M} \ket{-+}_{L} &\rightarrow \ket{-}_{L}  \tag{69}
\end{align}

のように定めることにすると、smooth merge後の状態は、

\ket{\psi} \odot \ket{\phi} = a \ket{\phi} + (-1)^{M} b Z_{L}^{\prime} \ket{\phi}  \tag{70}

となります。これがsmooth mergeの基本公式です。これも後で使いますので覚えておきましょう。

Lattice splitting

平面符号で表した1つの論理量子ビットを2つの論理量子ビットに分離する操作のことをlattice splittingと呼びます。分離した境界がrough boundaryになる操作をrough splitと呼び、smooth boundaryになる操作をsmooth splitと呼びます。

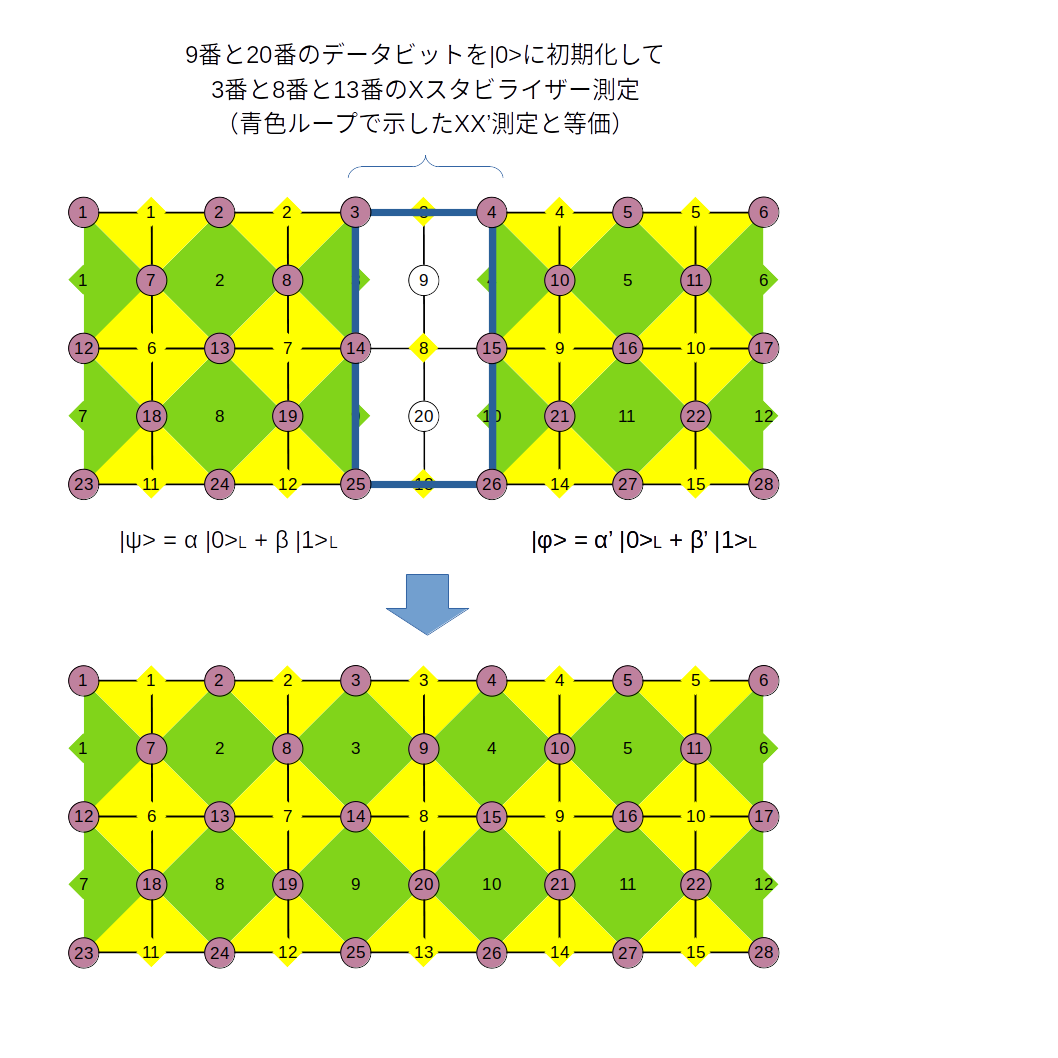
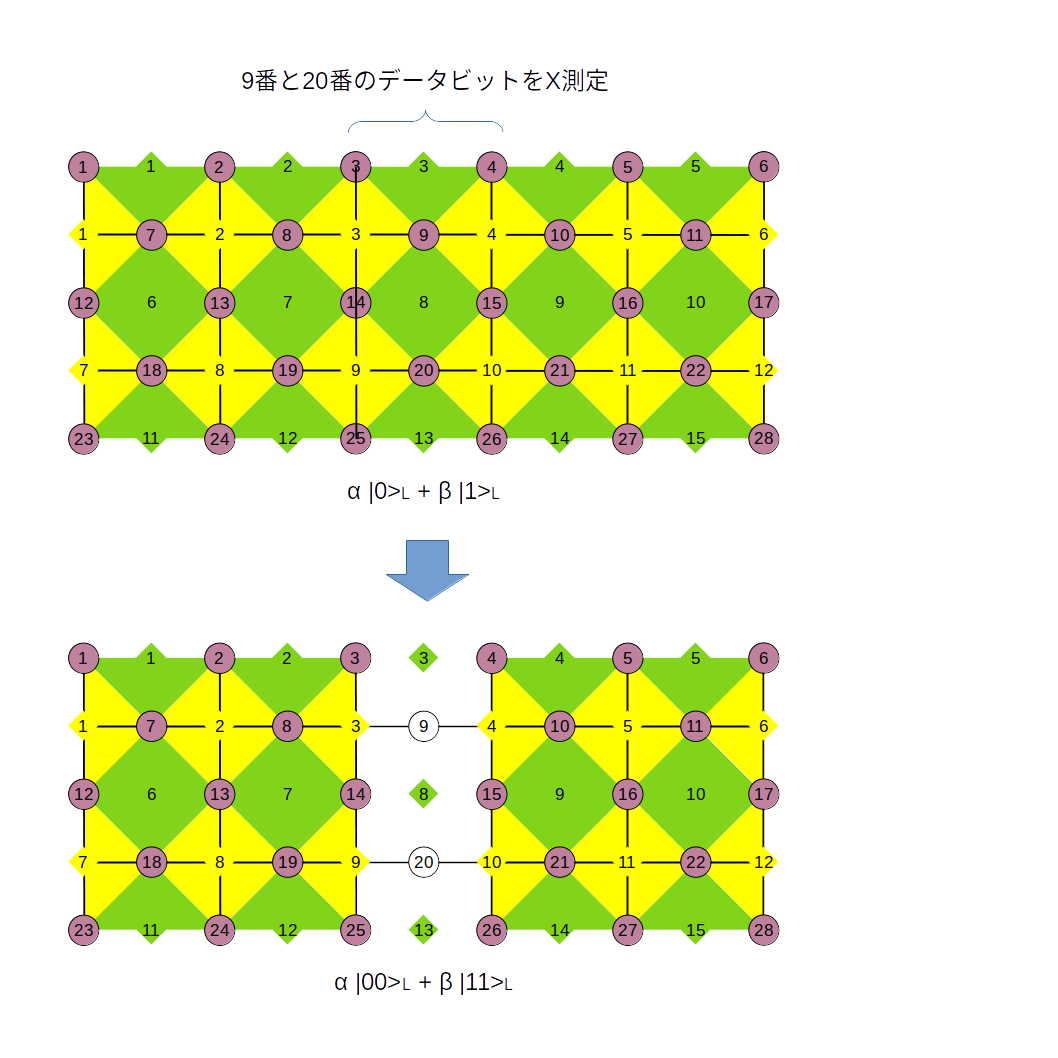
まず、smooth splitについて考えます。下図に示す格子において論理状態が、

\alpha \ket{0}_{L} + \beta \ket{1}_{L}  \tag{71}

で与えられているとします。smooth splitは真ん中の量子ビット（9番と20番）を$X$測定する操作です。この測定で真ん中に位置する$Z$スタビライザーが消えてなくなり左右に分離した状態になります。本当にそうなるか数式の上で確認してみます。$\ket{0}_{L}$と$\ket{1}_{L}$が各々どう変化するか数式の上で確認してみます。$\ket{0}_{L}$はスタビライザー形式で書くと、

<\bar{X_1}, \cdots , \bar{X_{12}}, \bar{Z_1}, \cdots , \bar{Z_{15}}, Z_{1} Z_{12} Z_{23}>  \tag{72}

と表わせます。この状態に対して、$X_{9}$測定してみます。$X_{9}$に反可換な演算子は$\bar{Z_3}$と$\bar{Z_8}$なので後者に前者をかけることで反可換な演算子を一つにしておいてから、$X_{9}$測定して測定値が$\mu_{9}$だったとすると、

<\bar{X_1}, \cdots , \bar{X_{12}}, \bar{Z_1}, \bar{Z_2}, \mu_{9} X_{9}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, Z_{3} Z_{4} Z_{14} Z_{15} Z_{20}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, \bar{Z_{13}}, \bar{Z_{14}}, \bar{Z_{15}}, Z_{1} Z_{12} Z_{23}> \tag{73}

という状態に変化します。さらに、$X_{20}$を測定します。$X_{20}$に反可換な演算子は$Z_{13}$と$Z_{3} Z_{4} Z_{14} Z_{15} Z_{20}$なので後者に前者をかけることで反可換な演算子を一つにしておいてから、$X_{20}$を測定して測定値が$\mu_{20}$だったとすると、

<\bar{X_1}, \cdots , \bar{X_{12}}, \bar{Z_1}, \bar{Z_2}, \mu_{9} X_{9}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, Z_{3} Z_{4} Z_{14} Z_{15} Z_{25} Z_{26}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, \mu_{20} X_{20}, \bar{Z_{14}}, \bar{Z_{15}}, Z_{1} Z_{12} Z_{23}> \tag{74}

となります。ここで、$\mu_{9} X_{9}$と$\mu_{20} X_{20}$をはさむ左右の4端子の$X$スタビライザーに$\mu_{9} X_{9}$と$\mu_{20} X_{20}$をかけて各々3端子にしておきます。さらに、$Z_{1} Z_{12} Z_{23}$と同値である$Z_{3} Z_{14} Z_{25}$を$Z_{3} Z_{4} Z_{14} Z_{15} Z_{25} Z_{26}$にかけると、

\begin{align}
&<\bar{X_1}, \bar{X_2}, \mu_{9} \bar{X_3}, \mu_{9} \bar{X_4}, \bar{X_5}, \bar{X_6}, \bar{X_7}, \bar{X_8}, \mu_{20} \bar{X_9}, \mu_{20} \bar{X_10}, \bar{X_11}, \bar{X_{12}}, \bar{Z_1}, \bar{Z_2}, \mu_{9} X_{9}, \bar{Z_4}, \bar{Z_5}, \bar{Z_6}, \bar{Z_7}, Z_{4} Z_{15} Z_{26}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{11}}, \bar{Z_{12}}, \mu_{20} X_{20}, \bar{Z_{14}}, \bar{Z_{15}}, Z_{1} Z_{12} Z_{23}> \\
&= <\bar{X_1}, \bar{X_2}, \mu_{9} \bar{X_3}, \bar{X_7}, \bar{X_8}, \mu_{20} \bar{X_9}, \bar{Z_1}, \bar{Z_2}, \bar{Z_6}, \bar{Z_7}, \bar{Z_{11}}, \bar{Z_{12}}, Z_{1} Z_{12} Z_{23}> \otimes <\mu_{9} X_{9}, \mu_{20} X_{20}> \otimes <\mu_{9} \bar{X_4}, \bar{X_5}, \bar{X_6}, \mu_{20} \bar{X_{10}}, \bar{X_{11}}, \bar{X_{12}}, \bar{Z_4}, \bar{Z_5}, \bar{Z_9}, \bar{Z_{10}}, \bar{Z_{14}}, \bar{Z_{15}}, Z_{4} Z_{15} Z_{26}> \tag{75}
\end{align}

となり、左の論理状態と真ん中の2つの孤立した量子ビットと右の論理状態という3つのパートにきれいに分かれるということになります。真ん中の2つの量子ビットを無視すると、左側は$Z_{1} Z_{12} Z_{23}$の固有値$+1$の固有状態で、右側は$Z_{4} Z_{15} Z_{26}$の固有値$+1$の固有状態であるため、結局、smooth splitによって、$\ket{0}_{L}$は、

\ket{0}_{L} \rightarrow \ket{00}_{L} \tag{76}

に変化することになります。同様の式展開によって$\ket{1}_{L}$は、

\ket{1}_{L} \rightarrow \ket{11}_{L} \tag{77}

に変化します。式(76)(77)を合わせると、式(71)は、

\alpha \ket{0}_{L} + \beta \ket{1}_{L} \rightarrow \alpha \ket{00}_{L} + \beta \ket{11}_{L}  \tag{78}

に変化します。これがsmooth splitの基本公式です。後で使いますので覚えておきましょう。

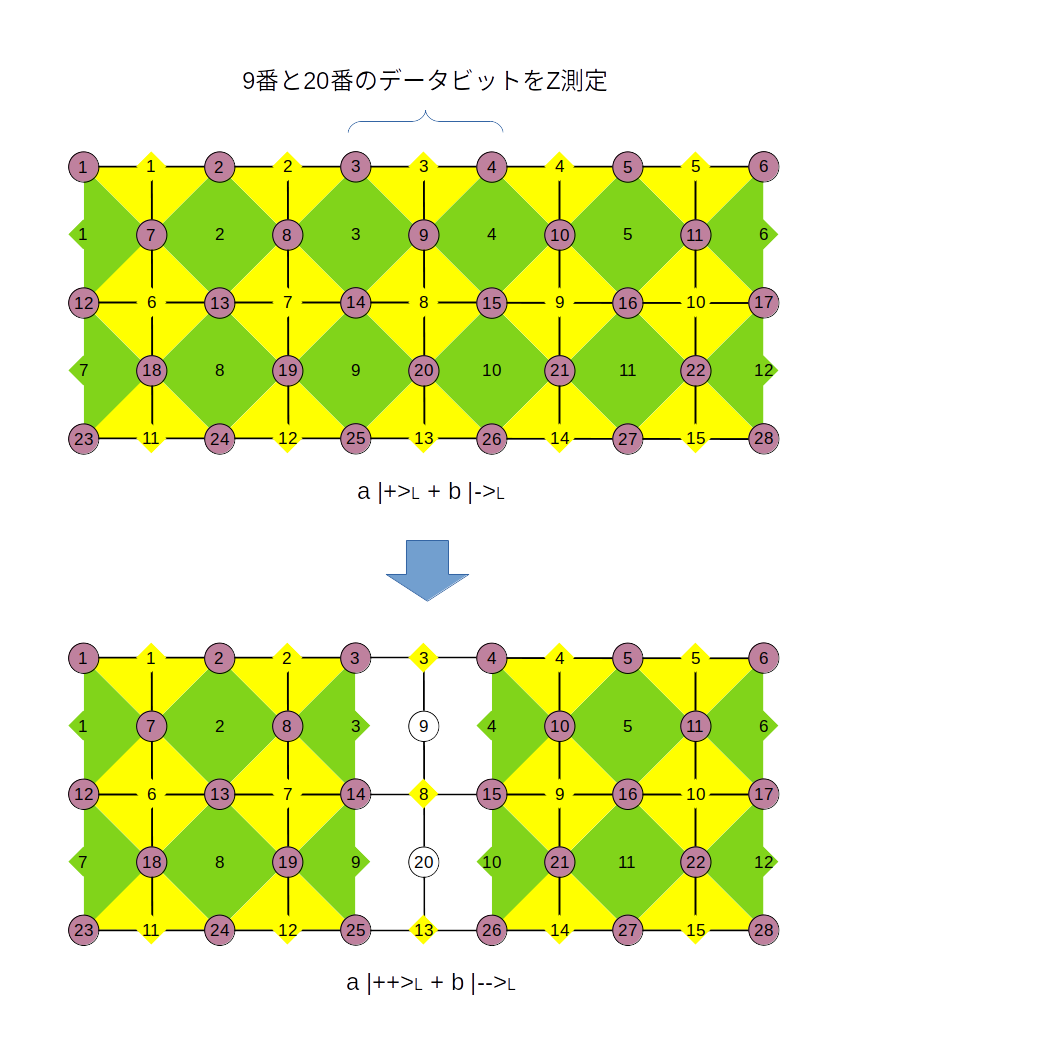
次に、rough splitについて考えてみます。下図に示す格子において論理状態が、

a \ket{+}_{L} + b \ket{-}_{L}  \tag{79}

で与えられているとします。rough splitは真ん中の量子ビット（9番と20番）を$Z$測定する操作です。この測定で真ん中に位置する$X$スタビライザーが消えてなくなり左右に分離した状態になります。smooth splitにおける$X$と$Z$を入れ替えれば先ほどと全く同じ式展開が成り立ち、結局、

a \ket{+}_{L} + b \ket{+}_{L} \rightarrow a \ket{++}_{L} + b \ket{--}_{L}  \tag{80}

となります。これがrough splitの基本公式です。これは後で使いません。が、基本公式として覚えておきましょう。

論理CNOT演算

それでは、本当に本当にお待たせしました！本日のメインイベント論理CNOT演算について語るときがやってきました！mergeしたりsplitしたりすることで論理CNOTが実現できるというマジックをこれからご披露します。でも、特に身構えないでも大丈夫です。今までの議論が理解できていればとても簡単な話です¹⁷。

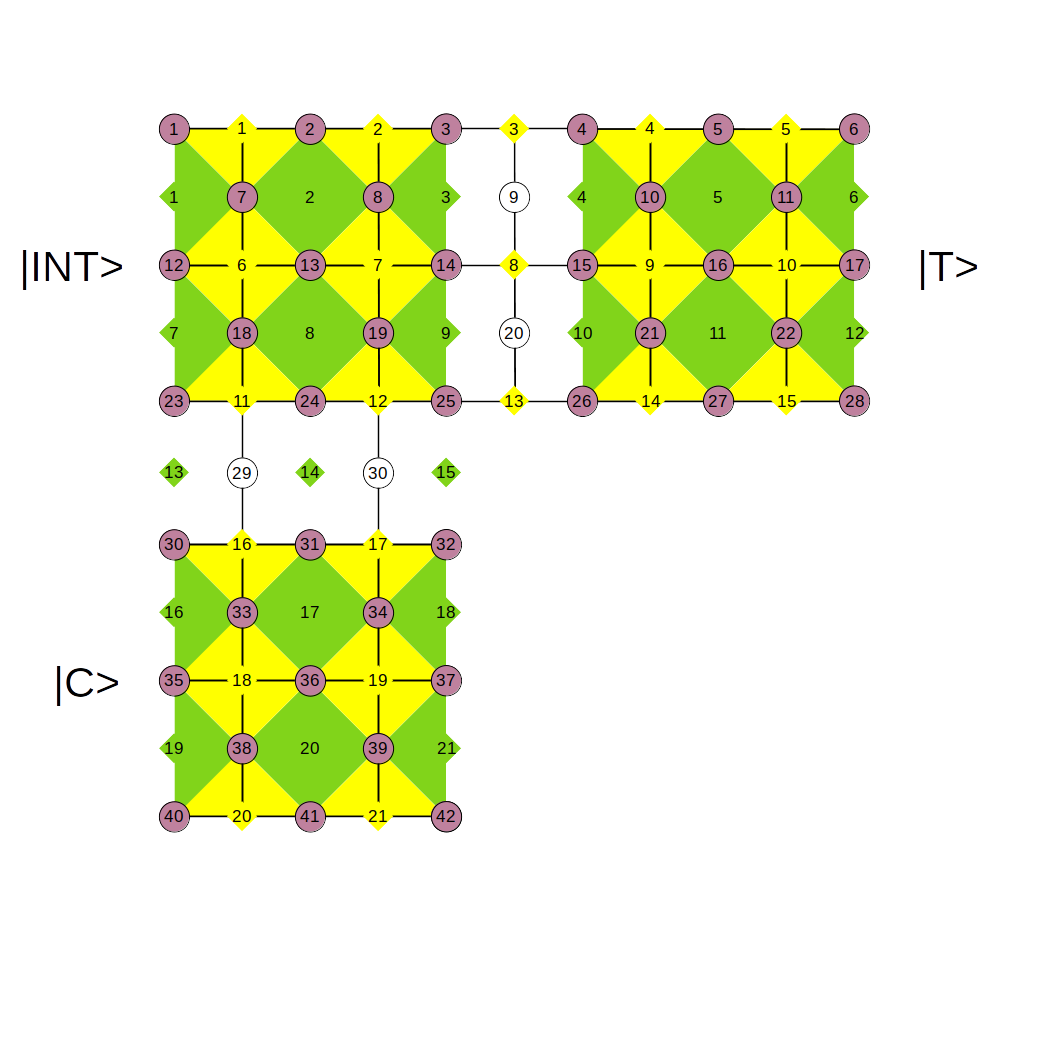
まず、下図に示すように3つの論理状態$\ket{C}, \space \ket{INT}, \space \ket{T}$があったとします。

$\ket{C}$はこれからやるCNOT演算の制御ビットで、

\ket{C} = \alpha \ket{0}_{L} + \beta \ket{1}_{L} = \bar{\alpha} \ket{+}_{L} + \bar{\beta} \ket{-}_{L}  \tag{81}

と表されるものとします。ここで、

\begin{align}
\bar{\alpha} = \frac{1}{\sqrt{2}} (\alpha + \beta)  \\
\bar{\beta} = \frac{1}{\sqrt{2}} (\alpha - \beta)  \tag{82}
\end{align}

とおきました。$\ket{T}$は標的ビットで、

\ket{T} = \alpha^{\prime} \ket{0}_{L} + \beta^{\prime} \ket{1}_{L}  \tag{83}

とします。$\ket{INT}$は補助的な役割をする論理状態で、

\ket{INT} = \ket{+}_{L}  \tag{84}

に初期化されているものとします。

さぁ、準備はできました。ここからCNOT演算を開始します。まず、$\ket{C}$と$\ket{INT}$をsmooth mergeします。式(70)を使うとmerge後の状態は、

\begin{align}
\ket{C} \odot \ket{INT} &= \bar{\alpha} \ket{+}_{L}  + (-1)^{M} \bar{\beta} \ket{-}_{L}  \\
&= \bar{\alpha} (\ket{0}_{L} + \ket{1}_{L}) + (-1)^{M} \bar{\beta} (\ket{0}_{L} + \ket{1}_{L})  \\
&= (\bar{\alpha} + (-1)^{M} \bar{\beta}) \ket{0}_{L} + (\bar{\alpha} - (-1)^{M} \bar{\beta}) \ket{1}_{L}  \tag{85}
\end{align}

となります。ここで、smooth mergeしたときの測定結果$M$が$0$だった場合何もせず、$1$だった場合論理パウリ$X$演算子をかけてビット反転します（あるいは、ビット反転したことを覚えておいて後で辻褄合わせをします）。そうすると、

\ket{C} \odot \ket{INT} = \alpha \ket{0}_{L} + \beta \ket{1}_{L}  \tag{86}

となります。次に、いまmergeしたばかりの論理状態をsmooth splitします。そうすると、

\ket{C} \odot \ket{INT} \rightarrow \ket{C^{\prime}} \ket{INT^{\prime}} = \alpha \ket{00}_{L} + \beta \ket{11}_{L}  \tag{87}

になります。さらに、今度は$\ket{INT^{\prime}}$を$\ket{T}$にrough mergeします。測定値を$M^{\prime}$とすると、

\begin{align}
\ket{C^{\prime}} (\ket{INT^{\prime}} \odot \ket{T}) &= \alpha \ket{0}_{L} (\ket{0}_{L} \odot \ket{T}) + \beta \ket{1}_{L} (\ket{1}_{L} \odot \ket{T}) \\
&= \alpha \ket{0}_{L} \ket{T} + \beta \ket{1}_{L} (-1)^{M^{\prime}} X_{L} \ket{T}  \tag{88}
\end{align}

となります。制御側が$\ket{0}_{L}$の場合、標的側は$\ket{T}$のままで、制御側が$\ket{1}_{L}$の場合、標的側はビット反転することになりますので、これでCNOT演算が完了したことになります。ただし、測定値$M^{\prime}$が$-1$だった場合、位相反転した結果を返しますので、その場合は制御側を位相反転します（あるいは位相反転したことを覚えておいて後で辻褄合わせをします）。また、式(88)の段階では、$\ket{INT^{\prime}}$と$\ket{T}$がmergeされて一体になった状態（横長の状態）なので、もとの姿に戻したい場合は$\ket{INT^{\prime}}$の各量子ビットを$Z$測定して縮小すれば良いです¹⁸。

シミュレーション

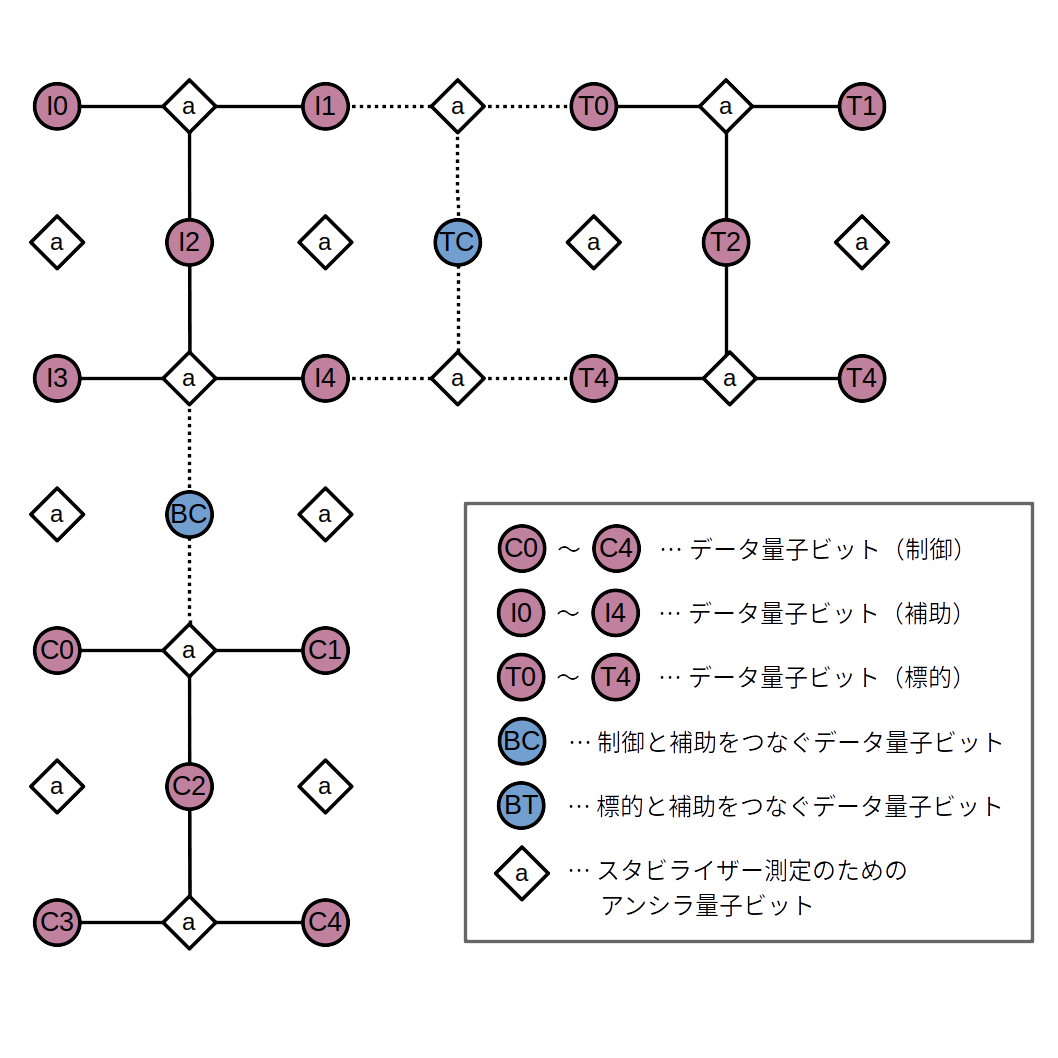
それでは、今説明したやり方で本当にCNOT演算が実現できるのかを量子計算シミュレータqlazyを使って確認してみます。下図に示したように簡易的に符号距離2の論理状態を3個用意してCNOT演算を実行してみます。

具体的には、マジック状態注入により制御側を$a \ket{0}_{L} + b \ket{1}_{L}$、標的側を$\ket{0}_{L}$にしておきます。すなわち、

\ket{C} \ket{T} = (a \ket{0}_{L} + b \ket{1}_{L}) \ket{0}_{L}  \tag{89}

にしておき、論理CNOT演算後に、

\ket{C^{\prime}} \ket{T^{\prime}} = a \ket{00}_{L} + b \ket{11}_{L}  \tag{90}

になることを確認します。最初の$a \ket{0} + b \ket{1}$をランダムに用意するために$U3$ゲートの3つの引数$\alpha, \beta, \gamma$をランダムに設定して、

U3(\alpha, \beta, \gamma) \ket{0} = a \ket{0} + b \ket{1}  \tag{91}

のように得ることにします¹⁹。

実装

全体のPythonコードを以下に示します。

import random
from qlazy import QState, PauliProduct
from qlazy.tools.Register import CreateRegister,InitRegister

class QStateLogical(QState):

    def set_register(self, dat_cnt, dat_int, dat_tar, bnd_cnt, bnd_tar, anc):

        self.__dat = {'cnt': dat_cnt, 'int': dat_int, 'tar': dat_tar}
        self.__bnd = {'cnt': bnd_cnt, 'tar': bnd_tar}
        self.__anc = anc
        self.__x_stab = {'cnt': [PauliProduct(pauli_str='XXX', qid=[dat_cnt[0], dat_cnt[1], dat_cnt[2]]),
                                  PauliProduct(pauli_str='XXX', qid=[dat_cnt[2], dat_cnt[3], dat_cnt[4]])],
                         'int': [PauliProduct(pauli_str='XXX', qid=[dat_int[0], dat_int[1], dat_int[2]]),
                                   PauliProduct(pauli_str='XXX', qid=[dat_int[2], dat_int[3], dat_int[4]])],
                         'tar': [PauliProduct(pauli_str='XXX', qid=[dat_tar[0], dat_tar[1], dat_tar[2]]),
                                   PauliProduct(pauli_str='XXX', qid=[dat_tar[2], dat_tar[3], dat_tar[4]])],
                         'bnd_tar': [PauliProduct(pauli_str='XXX', qid=[dat_int[1], dat_tar[0], bnd_tar[0]]),
                                     PauliProduct(pauli_str='XXX', qid=[bnd_tar[0], dat_int[4], dat_tar[3]])]}
        self.__z_stab = {'cnt': [PauliProduct(pauli_str='ZZZ', qid=[dat_cnt[0], dat_cnt[2], dat_cnt[3]]),
                                  PauliProduct(pauli_str='ZZZ', qid=[dat_cnt[1], dat_cnt[2], dat_cnt[4]])],
                         'int': [PauliProduct(pauli_str='ZZZ', qid=[dat_int[0], dat_int[2], dat_int[3]]),
                                   PauliProduct(pauli_str='ZZZ', qid=[dat_int[1], dat_int[2], dat_int[4]])],
                         'tar': [PauliProduct(pauli_str='ZZZ', qid=[dat_tar[0], dat_tar[2], dat_tar[3]]),
                                 PauliProduct(pauli_str='ZZZ', qid=[dat_tar[1], dat_tar[2], dat_tar[4]])],
                         'bnd_cnt': [PauliProduct(pauli_str='ZZZ', qid=[dat_cnt[0], bnd_cnt[0], dat_int[3]]),
                                     PauliProduct(pauli_str='ZZZ', qid=[dat_cnt[1], bnd_cnt[0], dat_int[4]])]}
        self.__lx = PauliProduct(pauli_str='XXXX', qid=[dat_int[0], dat_int[3], dat_cnt[0], dat_cnt[3]])
        self.__lz = PauliProduct(pauli_str='ZZZZ', qid=[dat_int[0], dat_int[1], dat_tar[0], dat_tar[1]])
        return self

    def __indirect_measure(self, pp, shots=1):  # 間接測定

        self.reset(qid=[self.__anc[0]])
        self.h(self.__anc[0])
        self.operate(ctrl=self.__anc[0], pp=pp)
        self.h(self.__anc[0])
        return self.m(qid=[self.__anc[0]], shots=shots)

    def initialize(self, alpha=0.0, beta=0.0, gamma=0.0):  # マジック状態注入
        ''' |cnt> = a |0> + b |1>, |tar> = |0> '''

        self.reset()
        self.u3(self.__dat['cnt'][0], alpha=alpha, beta=beta, gamma=gamma)
        self.cx(self.__dat['cnt'][0], self.__dat['cnt'][3])
        self.h(self.__dat['int'][0])
        self.cx(self.__dat['int'][0], self.__dat['int'][3])
        for site in ['cnt', 'int', 'tar']:
            for x_stab in self.__x_stab[site]:
                mval = self.__indirect_measure(x_stab).last
        return self

    def merge_cnt_int(self):  # 制御ビットと補助ビットのマージ

        parity = 0
        self.reset(qid=self.__bnd['cnt'])
        self.h(self.__bnd['cnt'][0])
        for z_stab in self.__z_stab['bnd_cnt']:
            parity += int(self.__indirect_measure(z_stab).last)
        if parity % 2 == 1: self.operate(pp=self.__lx)
        return self

    def merge_int_tar(self):  # 補助ビットと標的ビットのマージ

        self.reset(qid=self.__bnd['tar'])
        for x_stab in self.__x_stab['bnd_tar']:
            self.__indirect_measure(x_stab)
        return self

    def split_cnt_int(self):  # マージされている制御ビット＆補助ビットをスプリット

        return self.mx(qid=[self.__bnd['cnt'][0]]).last

    def measure(self, shots=1):  # 論理パウリZの測定

        return self.__indirect_measure(self.__lz, shots=shots).frequency

if __name__ == '__main__':

    shots = 100
    alpha, beta, gamma = random.uniform(0, 1), random.uniform(0, 1), random.uniform(0, 1)
    print("- alpha, beta, gamma = {:.4f}, {:.4f}, {:.4f}".format(alpha, beta, gamma))

    dat_cnt, dat_int, dat_tar = CreateRegister(5), CreateRegister(5), CreateRegister(5)
    bnd_cnt, bnd_tar, anc = CreateRegister(1), CreateRegister(1), CreateRegister(1)
    qubit_num = InitRegister(dat_cnt, dat_int, dat_tar, bnd_cnt, bnd_tar, anc)

    qs_logical = QStateLogical(qubit_num).set_register(dat_cnt, dat_int, dat_tar, bnd_cnt, bnd_tar, anc)
    qs_logical.initialize(alpha=alpha, beta=beta, gamma=gamma)
    qs_logical.merge_cnt_int()
    qs_logical.split_cnt_int()
    qs_logical.merge_int_tar()

    result_logical = qs_logical.measure(shots=shots)
    print("- actual =", result_logical)

    result = QState(qubit_num=1).u3(0, alpha=alpha, beta=beta, gamma=gamma).m(shots=shots)
    print("- expect =", result.frequency)

何をやっているか簡単に説明します。main処理部を見てください。

shots = 100
alpha, beta, gamma = random.uniform(0, 1), random.uniform(0, 1), random.uniform(0, 1)

で、測定回数を表す変数に100を入れて、ランダム状態を得るため$U3$ゲートに与える引数alpha, beta, gammaにランダム値を入れています。

dat_cnt, dat_int, dat_tar = CreateRegister(5), CreateRegister(5), CreateRegister(5)
bnd_cnt, bnd_tar, anc = CreateRegister(1), CreateRegister(1), CreateRegister(1)
qubit_num = InitRegister(dat_cnt, dat_int, dat_tar, bnd_cnt, bnd_tar, anc)

で、3つの論理ビットを構成するための物理量子ビット番号のリストを設定しています。dat_cnt,dat_int,dat_tarは各々論理的な制御ビット、補助ビット、標的ビットのビット番号リストです。bnd_cntは制御ビットと補助ビットの境界ビット、bnd_tarは標的ビットと補助ビットの境界ビット、ancはアンシラビット²⁰の番号リストを表しています（リストと言ってもこの場合要素数は1個です）。

qs_logical = QStateLogical(qubit_num).set_register(dat_cnt, dat_int, dat_tar, bnd_cnt, bnd_tar, anc)

ここで、QStateLogicalが出てきました。これはQStateを継承したサブクラスです²¹。main部の上の方でサブクラスを定義して必要なメソッドを追加しています。QStateLogicalのインスタンスを生成した後、すかさずset_registerメソッドで量子ビット番号を内部的に設定します。

次に、

qs_logical.initialize(alpha=alpha, beta=beta, gamma=gamma)

で、初期化します。内部的には先ほど得たalpha, beta, gammaを使って、式(89)に示した論理状態をマジック状態注入によって作成しています。後は、論理CNOT演算の手順に従い、

qs_logical.merge_cnt_int()

で、制御ビットと補助ビットをmergeし、

qs_logical.split_cnt_int()

で、mergeしたものをsplitし、

qs_logical.merge_int_tar()

で、補助ビットと標的ビットをmergeします。そして、最後に、

result_logical = qs_logical.measure(shots=shots)
print("- actual =", result_logical)

で、論理パウリ$Z$演算子を測定して、結果（$\ket{0}_{L}$の頻度と$\ket{1}_{L}$の頻度）を表示します。

これが正しいかどうかは、

result = QState(qubit_num=1).u3(0, alpha=alpha, beta=beta, gamma=gamma).m(shots=shots)
print("- expect =", result.frequency)

で、普通のCNOT演算の結果を表示することで確認します。両者の結果が大体同じになっていれば、論理CNOTが正しく実行されたと思って良いです。

動作確認

上のプログラムを実行した出力例を以下に示します。alpha, beta, gammaをランダムに生成しているので、実行のたびに測定値の頻度は変わります。例えば、

- alpha, beta, gamma = 0.5885, 0.6674, 0.1516
- actual = Counter({'0': 93, '1': 7})
- expect = Counter({'0': 96, '1': 4})

- alpha, beta, gamma = 0.3068, 0.8457, 0.4637
- actual = Counter({'0': 58, '1': 42})
- expect = Counter({'1': 52, '0': 48})

- alpha, beta, gamma = 0.2264, 0.2124, 0.7302
- actual = Counter({'1': 82, '0': 18})
- expect = Counter({'1': 81, '0': 19})

となりました。alpha,beta,gammaの値が様々に変わっても、actualとexpectで大体同じ頻度が得られていることから、正しく論理CNOT演算がシミュレーションできていることが確認できました。

おわりに

今回、スタビライザーの計算をきっちりやったので、かなりまだるっこしい説明になったかもしれませんが、測定結果による符号の反転がどこにどう反映されるのか、自分できちんと確認しておきたかったので、少し手間かけてやってみました。おかげで実装を想定した際の要注意ポイントがわかり理解が進みました。

さて、次回以降どんな話題を取り上げるか、例によって未定ですが、いましばらくは誤り訂正にこだわってみようと思っています。最近FTQC（誤り耐性のある量子コンピュータ）関連で新しい成果が発表されていて²²、業界的にになかなか面白い状況になってきた感があります。ありますが、まだまだ自分自身話についていけないところも多く、凄い！という噂の論文を見ても、その凄さや重大さが十分にわからんという状況にあり、何とかそれを味わえるレベルになりたいという思いがあります。というわけで、引き続き気まぐれ＆マイペースになりますが、ひとつひとつ潰していきたいと思っています。

以上

イオントラップ方式であれば遠距離間の演算も大丈夫らしいのですが、超電導方式など他の方式の多くでは遠距離演算は難しいと思うので。 ↩
このようなタイプの格子であればどんなサイズの格子を考えても表現できる論理量子ビットは必ず$1$になります。 ↩
何でも良いと言っても、いま考えているスタビライザー群を含むパウリ群の要素をもってくるのですが...。 ↩
$Z$演算子をトランスバーサルに構成したものが論理$Z$演算子になっていてフォールトトレラントで、かつ、わかりやすいのでこういう定義にしているのだと思います（たぶん）。 ↩
図で示したのは一例です。$Z$境界（rough boundary）同士を横方向につないだものであれば、何でも論理$Z$演算子とみなして良いですし、$X$境界（smooth boundary）同士を縦方向につないだものであれば、何でも論理$X$演算子とみなして良いです。例えば、$X_{L} = X_{2} X_{7} X_{12}, \space Z_{L} = Z_{6} Z_{7} Z_{8}$等々でもOKです。 ↩
これ大丈夫でしょうか。$U$をパウリ群の要素つまりパウリ積（pauli product）とすると$(I+U)/2$は$U$の固有値$+1$に対する固有空間への射影になります。式(13)はこのような固有空間への射影の射影の射影の、、、という具合に繰り返すことで同時固有状態を得る形になっています。 ↩
$\alpha \ket{0}_{L} + \beta \ket{1}_{L}$は$\alpha \ket{00 \cdots 0} + \beta \ket{11 \cdots 1}$のことではありませんので、お間違いなく。 ↩
$\bar{X_7}, \bar{X_8}, \bar{X_9}$の測定値に依存して対応したスタビライザーの固有値が反転しますのでご注意ください。反転している場所を覚えておけば後の論理演算には支障ありません（と思います）。 ↩
$\bar{Z_7}, \bar{Z_8}, \bar{Z_9}$の測定値によって対応したスタビライザーの固有値が反転しますのでご注意ください。反転している場所を覚えておけば後の論理演算には支障ありません（と思います）。 ↩
1番最後の等式で新しい格子における論理パウリ$Z$演算子を$Z_L = Z_{1} Z_{2} Z_{3}$としていますが、$Z_{6} Z_{7} Z_{8}$でも$Z_{11} Z_{12} Z_{13}$だと思っても良いです。要するにもとの論理パウリ$Z$演算子と同じものと考えて良いです。 ↩
気持ち悪い人は論理パウリ$X$を演算すれば、とりあえず論理パウリ$Z$の符号を反転させることができます。が、言うまでもないですが、限られたコヒーレンス時間の中でこういう演算を都度やってしまうのは賢いやり方ではありません。 ↩
気持ち悪い人は論理パウリ$Z$を演算すれば、とりあえず論理パウリ$X$の符号を反転させることができます。が、言うまでもないですが、限られたコヒーレンス時間の中で、、以下略。 ↩
量子チップを3次元的に構成するみたいなことは、もしかすると割と最近になって現実感が出てきた話なのかもしれません。が、すみません。このあたりよくわかっていません、汗。 ↩
$X_{L}$を間接測定してから$X_{L}^{\prime}$を間接測定するという意味ではありませんので、念の為。 ↩
参考文献1では丸付きのMでmergeを表しているのですが、Qiitaでどうやって記述するかわからなかったので（多分できない？）、代わりに$\odot$としました。 ↩
ないけどあると思ってください、心の眼を使って！ ↩
簡単なのですが、これ最初に思いついた人はすごいと思います。 ↩
このとき測定値に応じて標的側の論理パウリ$Z$演算子の符号が逆転する場合があることにご注意ください。つまり、$\ket{0}_{L}$と$\ket{1}_{L}$が入れ替わるかもしれません。その場合論理パウリ$X$演算子を演算すれば元に戻ります（あるいはビット反転したことを覚えておいて後で辻褄合わせをします）。 ↩
qiskitのドキュメントでは、$U3$の引数は$U3(\theta, \phi, \lambda)$のように書いてあると思いますが、qlazyではその引数は$\alpha,\beta,\gamma$と定義してまして、各々$\alpha \rightarrow \lambda, \space \beta \rightarrow \phi, \space \gamma \rightarrow \theta$のように読み替えてください。また、角度の単位は$\pi$ラジアンとしていますので、$\alpha=0.5$は$\pi/2$を表しています。 ↩
各スタビライザーに対して1つのアンシラが対応するように配備するのが普通ですが、シミュレータの量子ビットをケチるため1個のアンシラを都度リセットして使い回します。 ↩
qlazyのv0.2.2で量子状態を表す基本クラスを継承したサブクラスが作れるようになりました。複雑な量子回路を実行するためにカスタムゲートが作りたくなることがあると思いますが、そんなとき便利に使えると思います。 ↩
例えば、"Demonstration of fault-tolerant universal quantum gate operations", arXiv:2111.12654 [quant-ph]では、2つの論理量子ビットに対するフォールトトレラントな演算をイオントラップ方式で実現したと報告されています。 ↩