量子情報理論の基本：表面符号によるユニバーサル量子計算（２）〜Braidingで論理アダマール演算〜

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

はじめに

前回の記事「量子情報理論の基本：表面符号によるユニバーサル量子計算（１）」では、平面格子上に構成された欠陥対をBraidingさせることで、論理CNOT演算が実現できることを見てきました。また、論理パウリ演算（$X$,$Z$）は、欠陥対をつなぐチェーン上の量子ビットに対するパウリ演算子の積、または一つの欠陥を囲むループ上の量子ビットに対するパウリ演算子の積で表すことができるのでした。ユニバーサルな量子計算を実現するためには、これら以外に「アダマール演算」と「位相シフト演算（$S$,$T$、およびそのエルミート共役）」が必要です。今回の記事では、そのうちの「アダマール演算」について勉強します。欠陥対のBraidingでどのように論理アダマール演算が実現できるのか一通り説明した後、量子計算シミュレータqlazyを使って、その動作を確認します。

参考にさせていただいたのは、以下の文献です¹。

1. Austin G. Fowler, Matteo Mariantoni, John M. Martinis, Andrew N. Cleland, "Surface codes: Towards practical large-scale quantum computation", arXiv:1208.0928 [quant-ph]

理論説明

Steane符号をベースにフォールトトレラントな論理アダマール演算を実現する際には、ただ単に各量子ビットに対して同じようにアダマールゲートを適用すれば良いのでした²。表面符号の場合も同じように各量子ビットに対するアダマールゲート適用すればいいんじゃない？と思われるかもしれませんが、それは違います。甘いです。平面格子上に面演算子と頂点演算子が敷き詰められていると想像してみてください。そこに$N$個の論理量子ビット（つまり、$N$個の欠陥対）が存在していて、その中の一つに対して論理的なアダマール演算を適用したいとします。全量子ビットに対して一斉にアダマールゲートを適用すると、すべての面演算子は頂点演算子に変わりすべての頂点演算子は面演算子に変わるので、結果余計な論理量子ビットにもアダマール演算がなされてしまうことになります。かと言って、アダマール演算したい欠陥対の領域だけに限ってアダマールゲートを適用したとすると、境界で妙な不整合が発生しそうです。という問題をうまく回避するために、少し込み入ったテクニックを使います。この「理論説明」の節で順に丁寧に説明していきます。

が、本題の前に、Braidingによる論理アダマール演算を理解するために知っておいたほうが良い補足事項がありますので、ここで取り上げておきます。

平面格子上の論理X演算子と論理Z演算子（もう一つの構成）

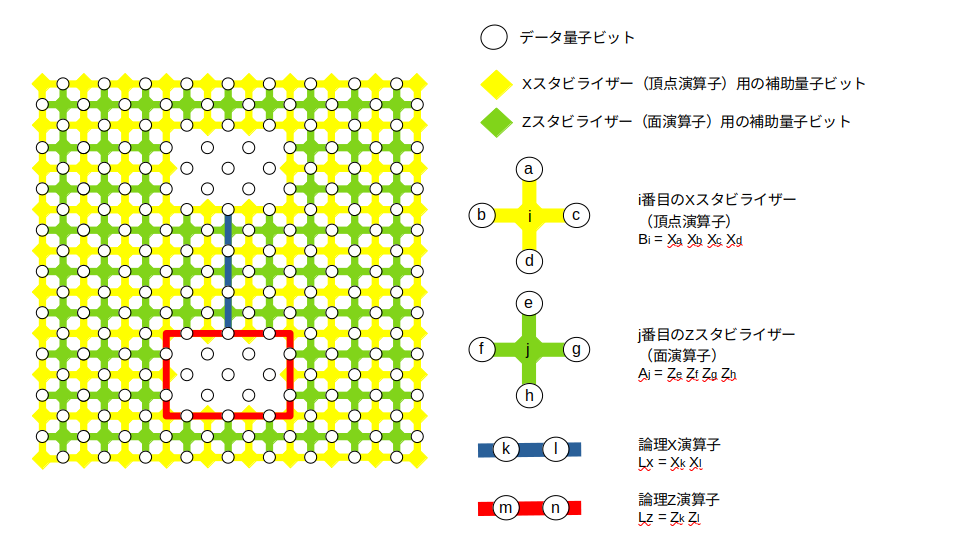
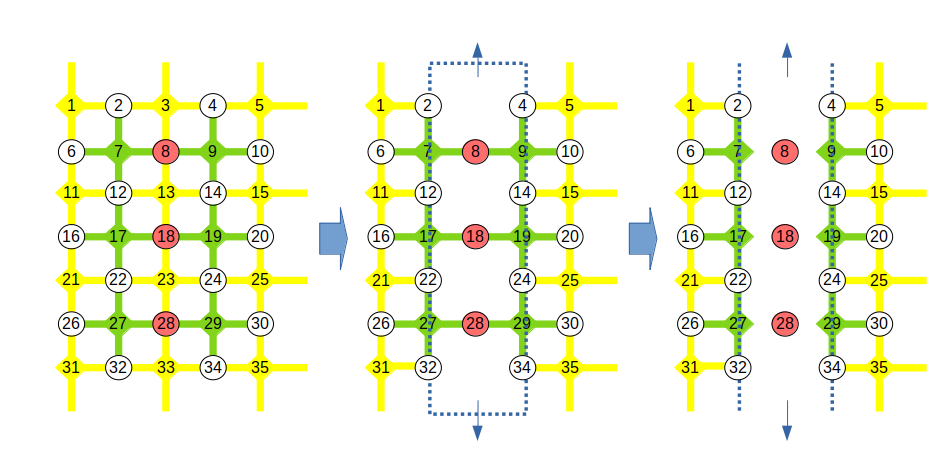
前回、前々回で考えていた平面格子は、下図のようなものでした。面演算子を欠陥にしたp型欠陥対の図になっていますが、頂点演算子を欠陥対にしたd型欠陥対というパターンもあります。ちなみに、面演算子（パウリ$Z$演算子の積）と頂点演算子（パウリ$X$演算子の積）という用語ですが、参考文献では各々「$Z$スタビライザー」「$X$スタビライザー」という用語が使われていたので、以後それに従うことにします。それから、下図の平面格子の書き方も前回までの記事と違っています。白丸はデータ量子ビットを表しています。緑色の十字は面演算子で中央のひし形が面演算子に対応した補助量子ビット、黄色の十字は頂点演算子で中央の黄色のひし形が頂点演算子に対応した補助量子ビットを表しています。これも参考文献のほぼ真似です。この図の方が説明がしやすいので、以後これで行きます。

さて、上図を改めてじっくり見てください。p型欠陥の周りを$X$スタビライザーが囲んでいる格好になっています。しかも欠陥の角を除く各辺に相当する場所の$X$スタビライザーは4端子ではなく3端子になっています³。このように$X$スタビライザーが並んでいる境界のことを「$X$境界(X boundary)⁴」と言います。論理$X$演算子は2つの$X$境界をつないだチェーン上の$X$演算子の積です。一方、論理$Z$演算子は$X$境界上の$Z$演算子の積です。

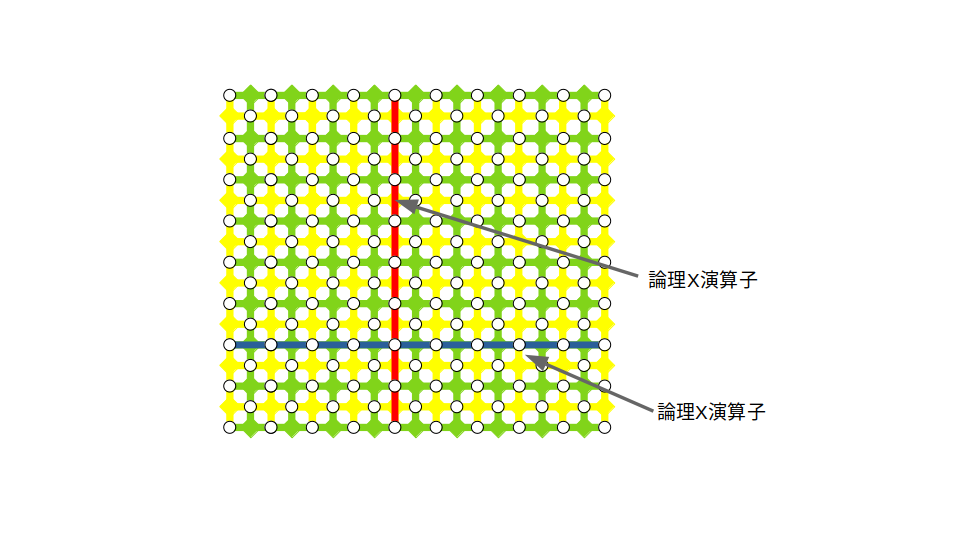
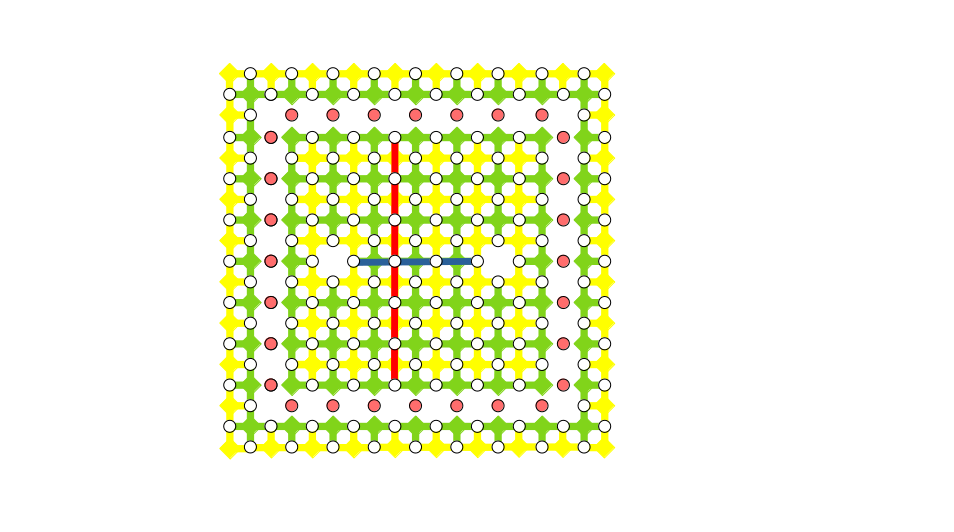
ということを踏まえると、欠陥がなくてもとにかく2つの$X$境界があれば、それをつなげるチェーンを考えることで論理$X$演算子が実現できそうです。下図に示した平面格子がまさにそれです。左右の辺が$X$境界です。それをつないだ$X$演算子の積が論理$X$演算子になっていることは簡単にわかると思います。すべてのスタビライザーと可換で、かつ、どんなスタビライザーの積でも表すことができないので（つまり独立なので）、これは論理$X$演算子と考えて良いです。一方、論理$Z$演算子は先ほどの説明からすると$X$境界上の$Z$演算子の積ということになります。例えば、一番左の辺が論理$Z$演算子だとしてみましょう。確かに、すべてのスタビライザーと可換になっていて、どんなスタビライザーの積でも表すことができず、かつ、論理$X$演算子と反可換です。下図ではそれを右にずらして真ん中あたりに持ってきていますが、同じように論理$Z$演算子の役割を果たします。上下の辺は「$Z$境界」になっているので、2つの$Z$境界をつなぐチェーン上の$Z$演算子が論理$Z$演算子になります、という言い方もできそうです。下図の例では、論理$X$演算子も論理$Z$演算子も直線で表現していますが、これは曲がりくねっていても全然OKです。とにかく2つの$X$境界をどんな形でも良いのでつないだものが論理$X$演算子で、2つの$Z$境界をどんな形でも良いのでつないだものが論理$Z$演算子です⁵。

補足事項は以上です。それでは、本題です。

論理アダマール演算の手順

さてどうやるか？結論を先に言います。大きく分けると、以下のような6ステップで論理アダマール演算は実現できます。

• 【STEP.1】お掘りを作って欠陥対を孤立させる
• 【STEP.2】お掘りの内部を縮小して欠陥対をなくす（穴のない一つの島にする）
• 【STEP.3】島を構成する量子ビットにアダマールゲートを適用する
• 【STEP.4】スワップによって島の位置を半格子ずらす
• 【STEP.5】島を拡張して欠陥対を作成する
• 【STEP.6】お掘りを埋めて元に戻す

「お掘」りとか「島」とか何のことかさっぱりわからないと思います。以下で詳細に説明します。

【STEP.1】お掘りを作って欠陥対を孤立させる

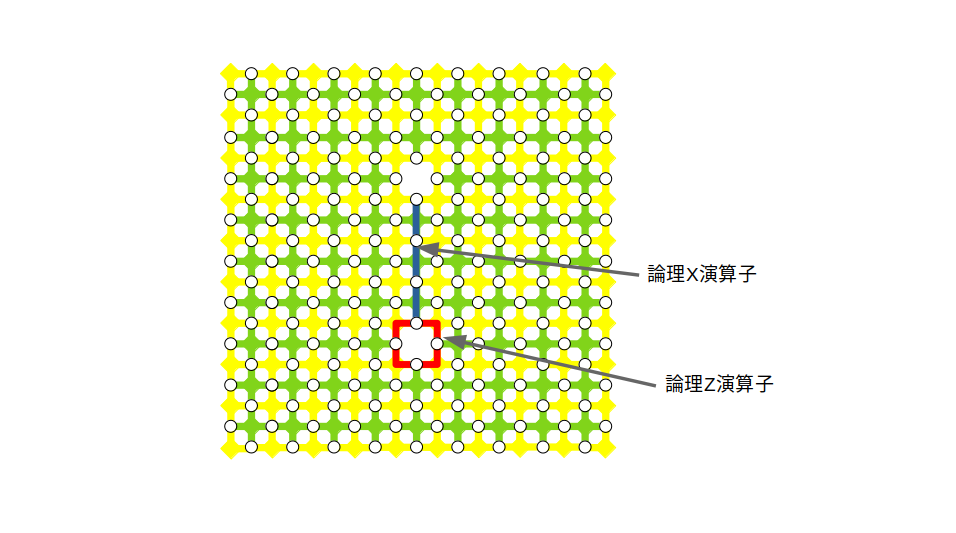
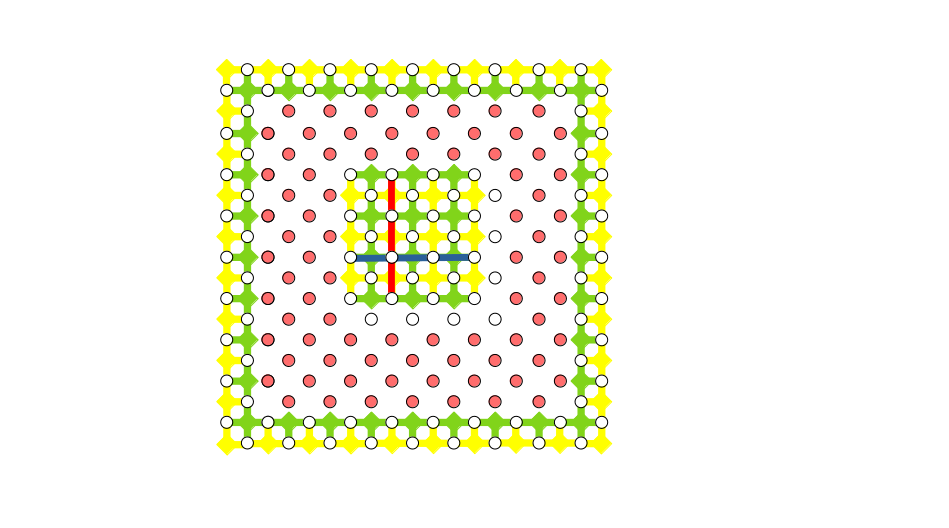
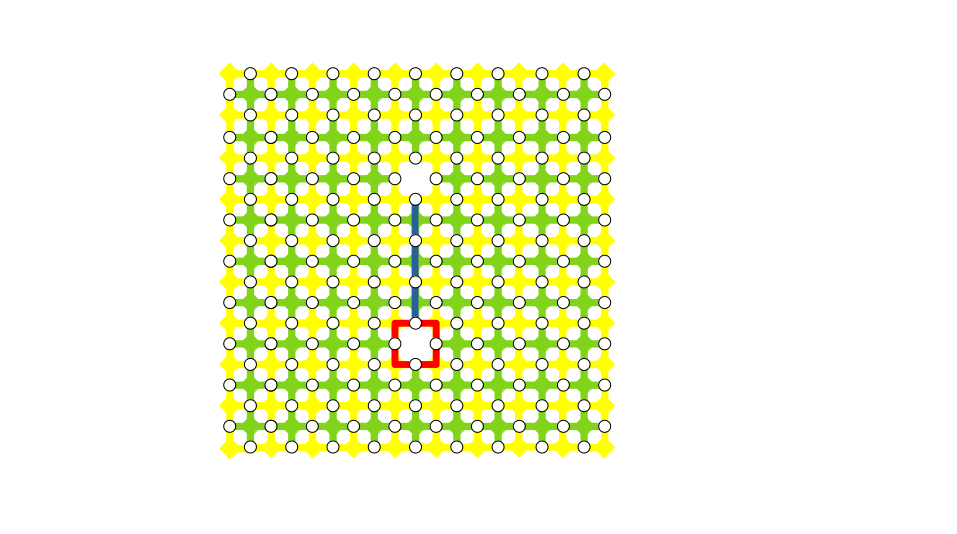
まず、論理アダマール演算を実行する入力量子状態があると思ってください。一つの欠陥対が一つの論理量子ビットを表しますので、論理$N$量子ビットの初期状態を用意するということは、$X$スタビライザーと$Z$スタビライザーが定義された、だだっ広い平面格子上に$N$個の欠陥対を作るということを意味しています。前回までの記事で見てきたように格子平面上のどこかのデータ量子ビットを$X$基底または$Z$基底で測定してできた欠陥対に対して拡張・削除を繰り返してその位置を移動させれば、適当な符号距離を持った欠陥対が出来上がるのでした。例えば最初にどこかの量子ビットを$X$基底で測定して欠陥対を移動させるとp型欠陥対ができて論理$\ket{\bar{+}}$状態を得ることができます（$+$の上のバーで論理量子ビットであることを表すことにします。以下同様）。この操作を格子平面の複数箇所で繰り返し実行すれば、論理$N$量子ビットに対する論理$\ket{\bar{+} \bar{+} \cdots \bar{+}}$が得られます。この初期状態に対して論理演算を実行することで量子計算を実現するわけです。ということで、これから実行しようとしている論理アダマール演算への入力量子状態のイメージができましたでしょうか。下図に示したような欠陥対が平面格子上にたくさん並んでいるイメージですね。ここで青線は論理$X$演算子、赤線は論理$Z$演算子を表しています。これを出発点にして、論理$X$演算子の立場と論理$Z$演算子の立場が入れ替わったら、論理アダマール演算が実現できたことになります。別の言い方をすると、例えば、論理$X$演算子の固有値1の固有状態$\ket{\bar{+}}$が論理$Z$の固有値1の固有状態$\ket{\bar{0}}$に変わったら、論理アダマール演算が実現できたことになります（後半の動作確認では、まさにこれを確認します）。

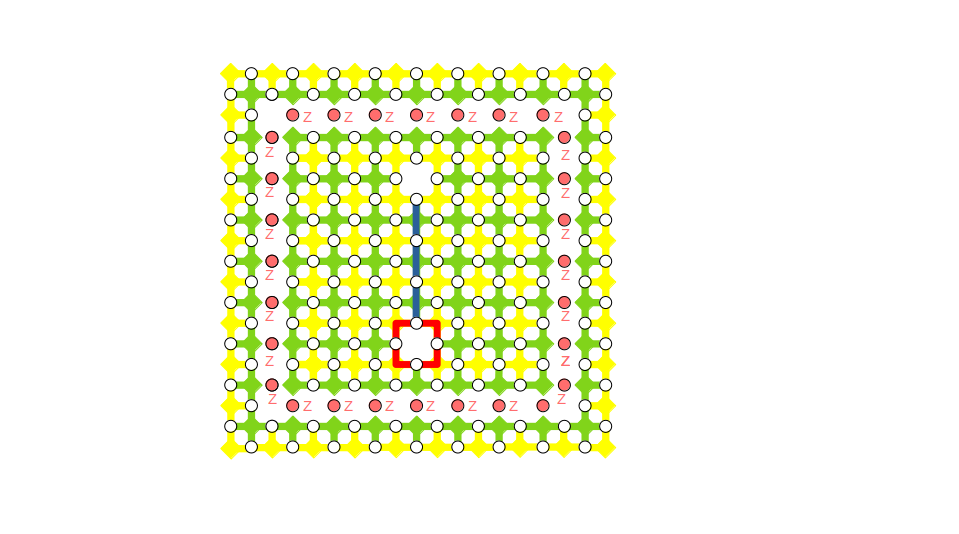
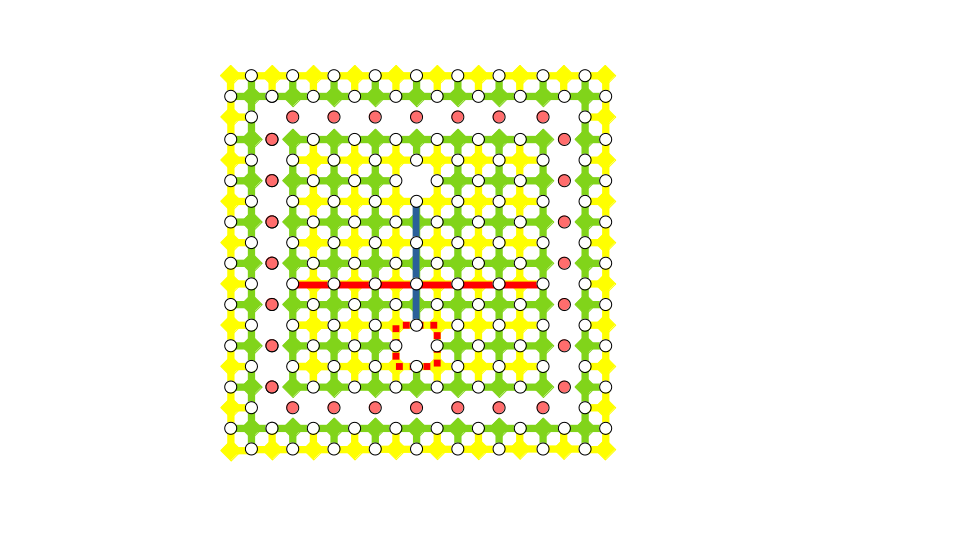
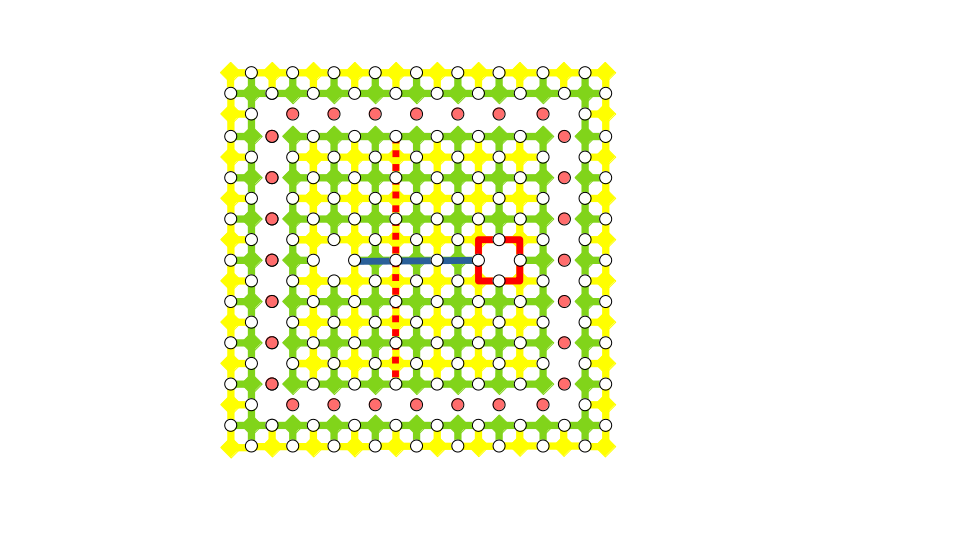
いま対象とする一つの論理量子ビットのみに論理アダマール演算を適用したいので、対象外の論理量子ビットにはその演算の影響が及ばないようにしておかないといけません。そのために対象としている欠陥対の周りにお掘りをつくって孤立させることをします。具体的には、下図に示すように、欠陥対を取り囲むデータ量子ビットを$Z$基底で測定します。測定をするとお掘りの内と外のエンタングルメントが一旦切れて、内と外のテンソル積状態になるので、内側の量子ビットにどんな操作をしても外の世界には全く影響を及ぼさない形になります。下図では測定する量子ビットをピンク色で示しました。ここで、お掘りに相当する部分のスタビライザーがきれいに取り除かれていますが、これはわかりますでしょうか。

最初のステップなので、少し丁寧に説明します。下図を見てください。お掘りにしたい部分を拡大してみました。

一番左の図を見てください。ピンク色で示した8番、18番、28番のデータ量子ビットを$Z$基底で測定するとします。測定前のスタビライザーは、

<e_{7} A_{7}, e_{9} A_{9}, e_{17} A_{17}, e_{19} A_{19}, e_{27} A_{27}, e_{29} A_{29}, e_{1} B_{1}, e_{3} B_{3}, e_{5} B_{5}, e_{11} B_{11}, e_{13} B_{13}, e_{15} B_{15}, e_{21} B_{21}, e_{23} B_{23}, e_{25} B_{25}, e_{31} B_{31}, e_{33} B_{33}, e_{35} B_{35}, \cdots >  \tag{1}

です。ここで、$A_{i}$は$i$番目の（補助量子ビットに対応した）$Z$スタビライザーを表します。例えば、$A_{7}=Z_{2} Z_{6} Z_{8} Z_{12}$です。$B_{i}$は$i$番目の（補助量子ビットに対応した）$X$スタビライザーを表します。例えば、$B_{13}=X_{8} X_{12} X_{14} X_{18}$です。$e_{i}$は$+1$または$-1$の符号を表します。表面符号の符号空間（真空状態）を作成する際に、$X$スタビライザーと$Z$スタビライザーを間接測定しますが、そのときの測定値（固有値）に対応します。

まず8番を$Z$測定してみます。すなわち、$Z_{8}$を測定します。$Z_{8}$と反可換なスタビライザーは$B_{3}$と$B_{13}$の2つなので一方を他方にかけることで、反可換なスタビライザーを一つにします。どっちをどっちに掛けても良いのですが、例えば、$e_{3} B_{3}, \space e_{13} B_{13} \rightarrow e_{3} e_{13} B_{3} B_{13}, \space e_{13} B_{13}$としてみます。$e_{3} e_{13} B_{3} B_{13}$は$B_{3}$と$B_{13}$を囲む$X$ループなので$Z_{8}$と可換です。一方、$e_{13} B_{13}$は$Z_{8}$と反可換なので、測定値に応じて$e_{13} B_{13}$を$e_{8} Z_{8}$に置き換えれば良いです（$e_{8}$が測定値です）。したがって、式(1)のスタビライザーは、

<e_{7} A_{7}, e_{9} A_{9}, e_{17} A_{17}, e_{19} A_{19}, e_{27} A_{27}, e_{29} A_{29}, e_{1} B_{1}, \mathbf{e_{3} e_{13} B_{3} B_{13}}, e_{5} B_{5}, e_{11} B_{11}, \mathbf{e_{8} Z_{8}}, e_{15} B_{15}, e_{21} B_{21}, e_{23} B_{23}, e_{25} B_{25}, e_{31} B_{31}, e_{33} B_{33}, e_{35} B_{35}, \cdots >  \tag{2}

という形に変化します。同様に18番と28番を$Z$測定すると、

<e_{7} A_{7}, e_{9} A_{9}, e_{17} A_{17}, e_{19} A_{19}, e_{27} A_{27}, e_{29} A_{29}, e_{1} B_{1}, e_{1} B_{1}, \mathbf{e_{3} e_{13} e_{23} e_{33} B_{3} B_{13} B_{23} B_{33}}, e_{5} B_{5}, e_{11} B_{11}, \mathbf{e_{8} Z_{8}}, e_{15} B_{15}, e_{21} B_{21}, \mathbf{e_{18} Z_{18}}, e_{25} B_{25}, \mathbf{e_{28} Z_{28}}, e_{33} B_{33}, e_{35} B_{35}, \cdots >  \tag{3}

となります。上図の真ん中に示されているように測定した$Z$演算子を含む$X$スタビライザーは消滅して、$Z$演算子および消滅した$X$スタビライザーを囲む$X$演算子のループ（上図青の点線で表現）に置き換わることがわかると思います。さらに$Z$測定を続けてお掘りを作るように一回りさせると、対応した$X$スタビライザーは消滅して$Z$演算子に置き換わり、さらに、$X$演算子のループだったものはお掘りを縁取る2つの$X$ループになります⁶。

ところで、お掘りの中に$Z$スタビライザーの一部もはみ出ています。例えば、$e_{7} A_{7} = e_{7} Z_{2} Z_{6} Z_{8} Z_{12}$の4端子のうち$Z_{8}$は、お掘りの中の$e_{8} Z_{8}$と共通の$Z$演算子を含みます。符号空間全体のスタビライザーを考えると、スタビライザー$e_{7} A_{7}$にスタビライザー$e_{8} Z_{8}$を掛けても状態としては変わらないので、そのように変更しても良いです。つまり、$e_{7} A_{7} = e_{7} Z_{2} Z_{6} Z_{8} Z_{12}$を$e_{7} e_{8} A_{7}^{\prime} = e_{7} e_{8} Z_{2} Z_{6} Z_{12}$のように置き換えても良いということです（$A_{7}^{\prime} = Z_{2} Z_{6} Z_{12}$のように定義しました）。ということで、お掘りの縁を形成するすべての$Z$スタビライザーを3端子に置き換えても良いということになります。結果、上図右のような形になります。

お掘りを作る作業は以上です。どうでしょう。イメージできましたでしょうか。符号の扱いがかなりややこしいので、一読ではなかなかわからないと思いますが、スタビライザー形式で測定をどう記述するのかに注意しながら、じっくり追っかけてみてください。

【STEP.2】お掘りの内部を縮小して欠陥対をなくす（穴のない一つの島にする）

論理$Z$演算子はループ状になっていますが、下図に示すように真っ直ぐに伸ばします。赤線よりも下にある$Z$スタビライザーを点線で示した論理$Z$演算子に掛けたとしても論理演算子としては同等の効果を表す演算子になりますので、赤い点線の$Z$ループと赤い実線の$Z$チェーンは同じ論理演算子を表すことになります。

ここで、赤線よりも下にある$Z$スタビライザーたちの符号にご注意ください。$Z$スタビライザーについているマイナスの符号の合計数が奇数個の場合、赤い点線の論理$Z$演算子は赤い実線の論理$-Z$演算子になります。これを論理$+Z$演算子としたい場合は、この状態に対して論理$X$演算子を施します。そうするとその符号は逆転します。さらに、ご注意いただきたいのは、お掘りに接している3端子の$Z$演算子の符号です。お掘りを作成するために測定した$Z$演算子の測定値の影響を受けて、もとの4端子の$Z$演算子の符号は変わっています。

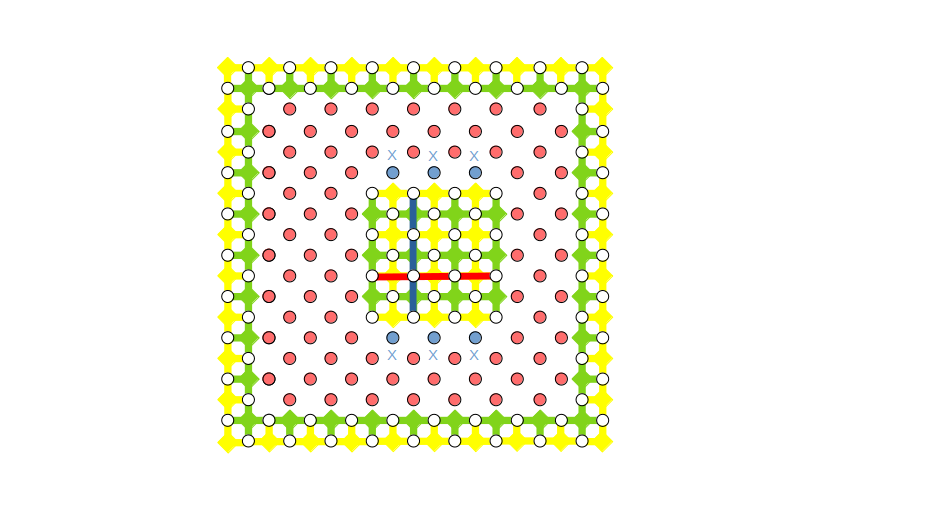
次に、お掘りの内部を縮小して欠陥のない島を作ります。縮小したい部分のデータ量子ビットを$Z$測定すれば、$X$スタビライザーは消滅します。同時に$Z$スタビライザーも消滅します。これは大丈夫でしょうか。$X$スタビライザーが消滅した部分はすべて$Z$演算子に置き換わります。$Z$スタビライザーの4端子（または3端子）に相当している4個（または3個）の$Z$演算子も各々スタビライザーとなっています。それらを$Z$スタビライザーに掛けても良いので、結局$Z$スタビライザーはないものと思って良いということになります（$Z$スタビライザーは恒等演算子に変わるので）。

これで島の大きさを任意に縮小することができますが、欠陥をなくして、かつ、赤い横線は論理$Z$演算子、青い縦線は論理$X$演算子のままにしておきたいので、下図に示すように、島の左右の境界を$Z$境界、上下の境界を$X$境界にするようにします（最初に示した補足事項を思い出してください）。そして、後の都合により、島の上下に隣接したデータ量子ビットについては$X$測定します（水色で示しました）。

【STEP.3】島を構成する量子ビットにアダマールゲートを適用する

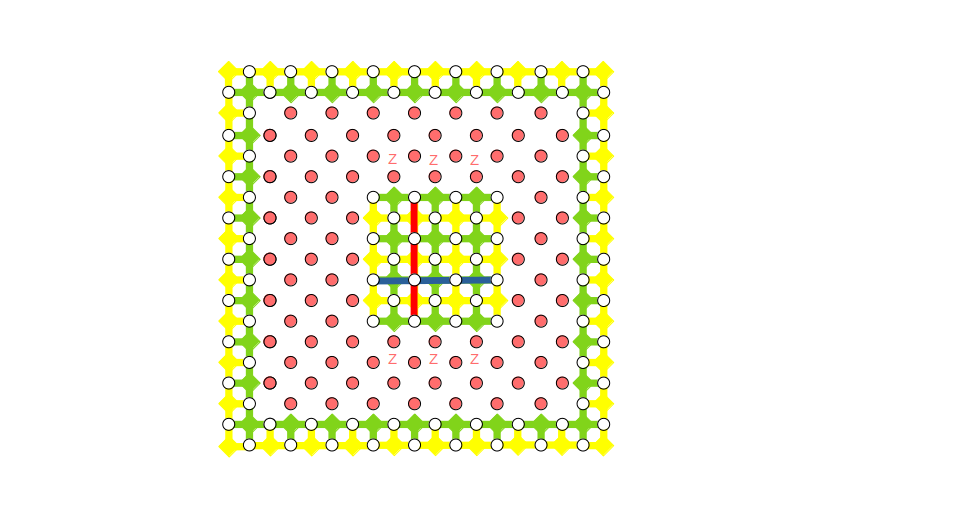
お待たせしました。本日のメインイベント！アダマールゲートの登場です。島を構成する全データ量子ビットと$X$測定した上下のデータ量子ビットを対象にして1量子ビットのアダマールゲートを適用します。そうすると、下図のようになります。すべての面演算子は頂点演算子に変わり、すべての頂点演算子は面演算子に変わります。そして、赤線だった論理$Z$演算子の$Z$チェーンは$X$チェーン（青線）に変わり、青線だった論理$X$演算子の$X$チェーンは$Z$チェーン（赤線）に変わります。これで論理$X$演算子と論理$Z$演算子の立場が逆転して、論理アダマール演算が実現されたことになります。

が、これで以上終了ではありません。もとの欠陥対の形に戻してあげないと、以降の論理演算が続けられません。ということで、後は、その形に戻す操作になります。

【STEP.4】スワップによって島の位置を半格子ずらす

アダマールによって、面演算子と頂点演算子が入れ替わったせいで、もともとの格子世界からみると半格子分ずれてしまったことになります。まずこれを是正します。スワップ演算によって、島を構成するデータ量子ビットを一斉に左斜め上に移動します。が、単純に左斜め上とスワップ演算をしてしまうのはよろしくないです。ちょっと考えればわかると思いますが、移動になりません。そこで、補助量子ビットをテンポラリとして、ステップを2つに分けます。まず、(1)すべてのデータ量子ビットを左隣の補助量子ビットとスワップさせます。次に、(2)移動したすべてのデータ量子ビットを一つ上の補助量子ビットとスワップさせます。これで、下図に示すように、左斜め上にデータ量子ビットが移動したことになります⁷。

【STEP.5】島を拡張して欠陥対を作成する

もとの欠陥対の形にしたいため、島を拡張すると同時に欠陥も作成します。島の外側で面演算子と頂点演算子を次々に測定していけば$X$スタビライザーと$Z$スタビライザーは復活します。このとき、下図に示すように、青線の左右に欠陥を残します。つまり、この欠陥に相当する$Z$スタビライザーは測定しません。また、お掘りの部分は残しておくようにします。赤線の$Z$チェーンはスタビライザー測定に応じて延長するようにしますが、その符号にご注意ください。もとの短い$Z$チェーンの上下端の$Z$演算子に接する$X$スタビライザーの測定値が論理$Z$演算子の符号に影響を及ぼします。符号逆転したくない場合は、測定値が$-1$になった場合、青線の論理$X$演算子を適用します。

縦の赤線で表された論理$Z$演算子は、下図に示すように右側の欠陥に巻き付いた$Z$ループと同等の効果を表します。ただし、またしても符号にご注意ください。$Z$チェーンを$Z$ループにするために必要な$Z$スタビライザーの符号によって論理演算子の符号が変わります。そうしたくない場合、青線の論理$X$演算子を適用してください。

【STEP.6】お掘りを埋めて元に戻す

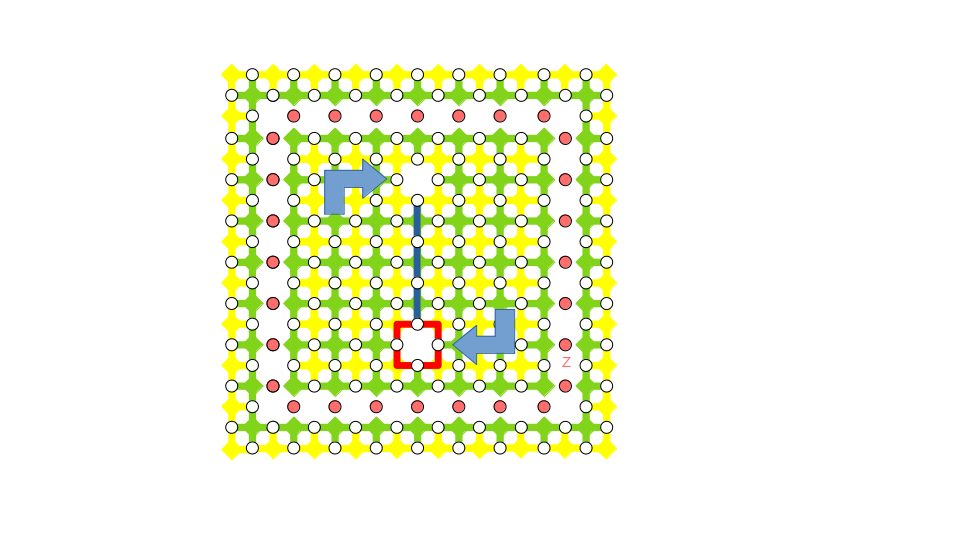
左右に並んだ欠陥をもとの上下に並んだ欠陥にするため、欠陥を移動します（下図）。移動のプロセスは以前の記事でも説明していたので省略します。

最後に、お掘りを埋めます。お掘りに隣接する3端子の$Z$スタビライザーを4端子に戻した上で、お掘りの中で$X$スタビライザーを測定すれば$X$スタビライザーが復活します。結果として、下図のように元の欠陥対の形に戻ります。最初の状態と全く同じように見えますが、アダマール演算によって論理$X$演算子と$Z$演算子の立場は入れ替わっています。例えば、最初論理$X$演算子の固有値$+1$の固有状態$\ket{\bar{+}}$だったとすると、いま説明したアダマール演算によって、論理$Z$演算子の固有値$+1$の固有状態$\ket{\bar{0}}$に変化しています。

動作確認

それでは量子計算シミュレータqlazyを使って、これで本当に論理アダマール演算が実現できるのかを確認してみます。前節の説明で使った格子サイズ（$9 \times 9$）で全く同じ場所に欠陥を作って同じように実装してみました。ただし、【STEP.6】の欠陥の移動は省略して左右に並んだままお掘りを埋めました。実装がそれなりに面倒で力尽きました（汗）。これでも、アダマールの効果は問題なく確認できるので、これで良しとしました。

実装

全体のPythonコードはここに置きました。ちょっと長くなってしまったので、骨組みとメイン部分だけを示します。とりあえず、雰囲気だけ見てください。v0.1.2で追加したQCompクラス（量子コンピュータを抽象化したクラスのつもり、、です）を継承させることで、表面符号における論理演算を実行するカスタム論理ゲートを定義しています。

import copy
import networkx as nx

from qlazypy import QComp, Backend
from qlazypy.tools.Register import CreateRegister, InitRegister

class QComp_SurfaceCode(QComp):

    def __init__(self, qubit_num=0, qid=None, backend=None):

    def initialize(self):
        """ 符号空間を初期化(真空状態を作成) """

    def set_logical_plus(self):
        """ 論理|+>状態を準備 """

    def operate_Lx(self):
        """ 論理パウリX演算 """

    def operate_Lh(self):
        """ 論理アダマール演算 """

    def measure_Lx(self, shots=1):
        """ 論理パウリX演算子の測定 """

    def measure_Lz(self, shots=1):
        """ 論理パウリZ演算子の測定 """

def main():

    row_length = 19
    col_length = 19
    qid = CreateRegister(row_length, col_length)  # 量子ビットは2次元配列(格子)に置く
    qubit_num = InitRegister(qid)
    
    bk = Backend(name='qlazy_stabilizer_simulator')
    qc = QComp_SurfaceCode(qubit_num=qubit_num, qid=qid, backend=bk)

    qc.initialize()        # 真空状態を作成
    qc.set_logical_plus()  # 論理|+>状態を準備
    qc.operate_Lh()        # 論理アダマール演算
    # qc.operate_Lx()        # 論理パウリX演算

    # result = qc.measure_Lz(shots=100)  # 論理パウリX演算子を測定
    result = qc.measure_Lz(shots=100)  # 論理パウリZ演算子を測定
    print("frequency =", result['frequency'])

    qc.free()

if __name__ == '__main__':
    main()

メイン部分の説明をします。

row_length = 19
col_length = 19
qid = CreateRegister(row_length, col_length)  # 量子ビットは2次元配列(格子)に置く
qubit_num = InitRegister(qid)

データ量子ビットと補助量子ビットを2次元格子に配列するための縦横のサイズをrow_length,col_lengthとします。今回の場合、先程の説明図をみていただければわかる通り、量子ビットは$19 \times 19$個あります。CreateRegister関数で量子レジスタ番号のリストqidを2次元配列、すなわち、19*19次元のリストのリストとして取得します。この段階ではqidの中身の要素はすべて0になっています。次のInitRegister関数によって、qidの要素として重複のない番号が0番から順に割り当てられます。そして、全体の量子ビット数をリターンします。

bk = Backend(name='qlazy_stabilizer_simulator')
qc = QComp_SurfaceCode(qubit_num=qubit_num, qid=qid, backend=bk)

バックエンドはqlazyのスタビライザー計算シミュレータを使います。前段で得たqubit_numとqidとバックエンドのインスタンスbkをQCompクラスを継承したQComp_SurfaceCodeクラスに与えて量子コンピュータ・クラスのインスタンスqcを生成します。このqcに対してカスタム定義した論理演算や測定を行っていきます。各メソッドの中身は省略していますので、後の処理は「そうなのね、ふーん」という具合に見ていただければと思います。

qc.initialize()        # 真空状態を作成
qc.set_logical_plus()  # 論理|+>状態を準備
qc.operate_Lh()        # 論理アダマール演算
# qc.operate_Lx()        # 論理パウリX演算

コメントに記載の通りです。真空状態（初期スタビライザー状態）を作成して、欠陥対を生成して$\ket{\bar{+}}$状態を用意し、それに論理アダマール演算を適用します。コメントアウトしていますが、さらに論理パウリ$X$演算を適用することも可能です。

result = qc.measure_Lz(shots=100)  # 論理パウリZ演算子を測定
# result = qc.measure_Lx(shots=100)  # 論理パウリX演算子を測定
print("frequency =", result['frequency'])

これもコメントに記載の通りです。論理パウリ$Z$を測定して結果をresultに格納して、頻度データを表示します。コメントアウトしていますが、論理パウリ$X$を測定することも可能です。

実行結果

まずは、上記ソースコード通りのパターンで実行してみました。

qc.initialize()        # 真空状態を作成
qc.set_logical_plus()  # 論理|+>状態を準備
qc.operate_Lh()        # 論理アダマール演算

result = qc.measure_Lz(shots=100)  # 論理パウリZ演算子を測定
print("frequency =", result['frequency'])

$\ket{\bar{+}}$を用意して論理アダマール演算するということなので、論理状態は$\ket{\bar{0}}$になっているはずです。したがって、100%の確率で'0'が測定されたら正常に動作していることになります。

frequency = Counter({'0': 100})

ということで、OKです。

次に、論理アダマール演算の後、論理パウリ$X$を演算してみたパターンです。

qc.initialize()        # 真空状態を作成
qc.set_logical_plus()  # 論理|+>状態を準備
qc.operate_Lh()        # 論理アダマール演算
qc.operate_Lx()        # 論理パウリX演算

result = qc.measure_Lz(shots=100)  # 論理パウリZ演算子を測定
print("frequency =", result['frequency'])

論理ビットが反転するだけなので、今度は'1'が100%になるはずです。

frequency = Counter({'1': 100})

ということで、こちらもOKです。

最後に、論理アダマール演算の後、論理$X$測定した場合です。

qc.initialize()        # 真空状態を作成
qc.set_logical_plus()  # 論理|+>状態を準備
qc.operate_Lh()        # 論理アダマール演算

result = qc.measure_Lx(shots=100)  # 論理パウリX演算子を測定
print("frequency =", result['frequency'])

測定方向が変わるので、'0'と'1'が半々の確率で出現するはずです。

frequency = Counter({'1': 52, '0': 48})

ということで、クリアです。めでたし、めでたし。動作確認は以上です。

おわりに

Braidingでの論理アダマール演算の手順を理解しシミュレータで実装までやってみましたが、やはりかなり面倒でした。特にスタビライザーの符号をきちんと考慮しないと逆の結果が出たり、実行のたびに結果が変わったりして、苦労しました。本質的には、すべての量子ビットにアダマールゲートをトランスバーサルにかけるのですが、特定の欠陥だけにその効果を及ぼすための前処理と後処理が大変です。おかげで、表面符号に関する理解が進んだ気がします。が、Lattice Surgeryの方が、このあたりの見通しが良さそうです（多分）。「はじめに」で述べたようにユニバーサル量子計算を実現するためには、さらに「位相シフト演算」も必要です。次回はそのあたりを取り上げる予定です。

以上

1. Braidingでアダマール演算を説明した日本語の文献がなかなかなく（自分の探し方が足りないせいかもしれませんが）、英語の文献で見つかったのがこれでした。というか、これ定番の論文ですよね（多分）。Braidingを使った量子計算が網羅的に記載されていて、とても参考になります。表面符号でBraidingしたい人は必須かなと。 ↩

2. 以前のこの記事参照。ちなみに、このような性質のことを「トランスバーサル性(transversality)」と言いました（復習です）。 ↩

3. p型欠陥（$Z$スタビライザーがない領域）を作る際に、その領域に相当する量子ビットに対して$X$測定を繰り返して欠陥領域を広げるという説明を以前しました。欠陥内部にいるスタビライザー（生成元）はすべて単なる$X$演算子たちなので、欠陥境界の4端子$X$スタビライザーに掛けてもスタビライザー状態としては同じです。ということを考えると、境界の$X$スタビライザーは3端子と思っても良いです。 ↩

4. 参考文献で使われていた"X boundary"を直訳して「$X$境界」としましたが、日本語の用語としてこういう言葉が浸透しているかどうかわかりません。本記事ではとりあえず「$X$境界」とか「$Z$境界」（あとで出てきます）ということにします。 ↩

5. $X$演算子のチェーンを量子状態に演算することと、$X$演算子のチェーンにそれと可換なスタビライザー（例えば、$X$スタビライザーの積）を掛けたものを量子状態に演算することは、状態に対して同じことをやっていることになります。つまり、同じ量子状態を出力します。トポロジー的に同値になるようにチェーンを変形しても論理演算子としては同じことを意味します、と言い換えても良いです。ただし、変形させるために掛けた$X$スタビライザーの各々の符号に注意しておく必要はあります。論理的な$X$演算子だったものが変形の結果、論理的な$-X$演算子に変わったりしますので。以上のことは、$Z$演算子のチェーンに関しても同様です。 ↩

6. より正確に言うと、お掘り部分に相当する$M$個の$X$スタビライザーは$M-1$個の$Z$演算子とお掘りを囲む二重の$X$ループ1個に置き換わります。二重の$X$ループは、次のステップで実施する$Z$測定で消滅します。 ↩

7. この手順によって補助量子ビットは右斜め下に移動してしまうことになりますが、補助量子ビットは間接測定のためのものであり、測定結果を得たらどうせ初期化するので、場所が変わったとしても何の影響もないため気にしないことにします。 ↩