$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
はじめに
フォールトトレラント量子計算を実現するためには各部品の誤り率が$10^{-4}=0.01%$程度以下で、かつ、連結符号という構成によって(Steane符号をベースとした場合)$7$の何乗個もの量子ビットが必要になるという話を前回しました。これで多くの人は絶望的な気分になるのですが、今回説明する「トポロジカル表面符号(topological surface code)」によって、希望の光が見えてくるはずです。
この後の節で何を説明しようとしているか最初に言っておきます。まず、「理論説明」ではトポロジカル表面符号(以下「表面符号」と呼ぶことにします)の符号状態と基本的な論理演算をどのように構成するかを述べ、その上で誤り訂正を上手に実行できることを説明します。「動作確認」では、量子計算シミュレータqlazyを使って、符号状態を作成してノイズを加え誤りを訂正するという一連の流れが正しく動作することを確認します。
参考にさせていただいたのは、以下の文献です。
- 小柴、森前、藤井「観測に基づく量子計算」コロナ社(2017年)
- 慶應義塾大学「量子コンピュータ授業 #14 幾何学符号」
- K.Fujii,"Quantum Computation with Topological Codes - from qubit to topological fault-tolerance",arXiv:1504.01444v1 [quant-ph] 7 Apr 2015
- 徳永「量子コンピュータの誤り訂正技術-物理に即したトポロジカル表面符号-」(2014年)
理論説明
表面符号の定義
面演算子と頂点演算子
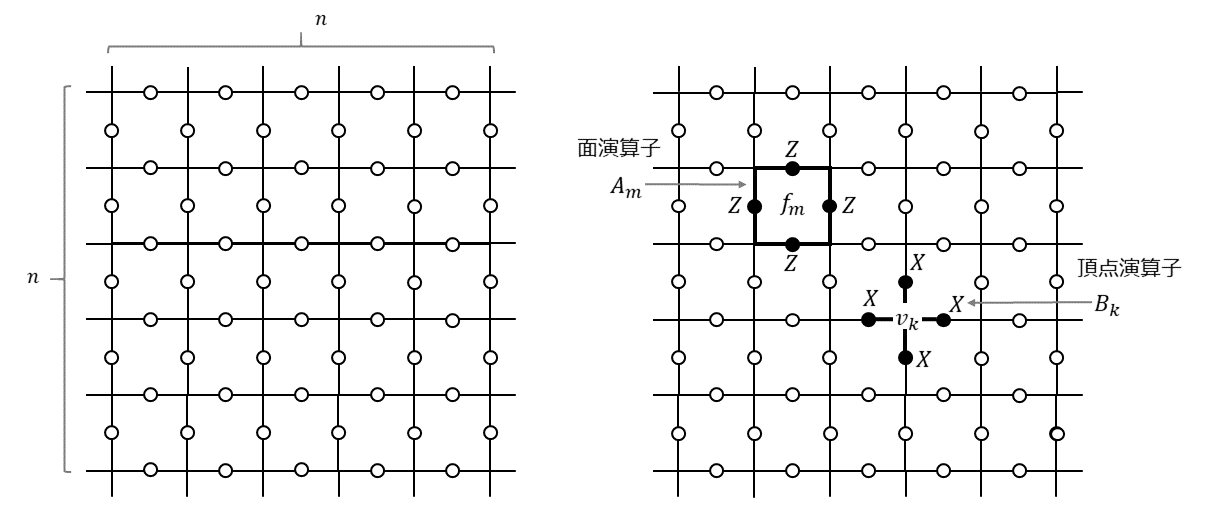
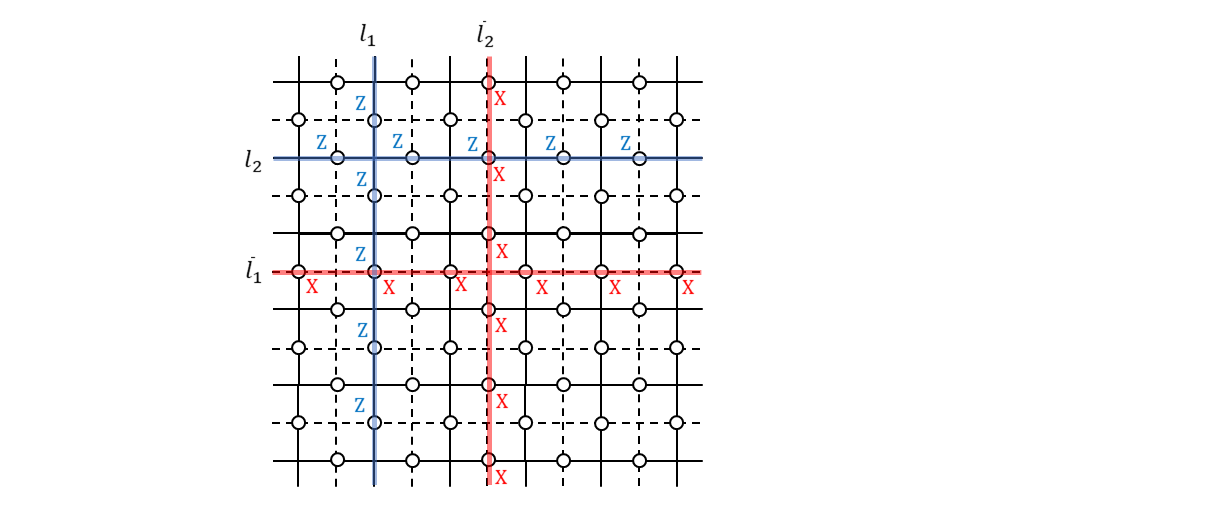
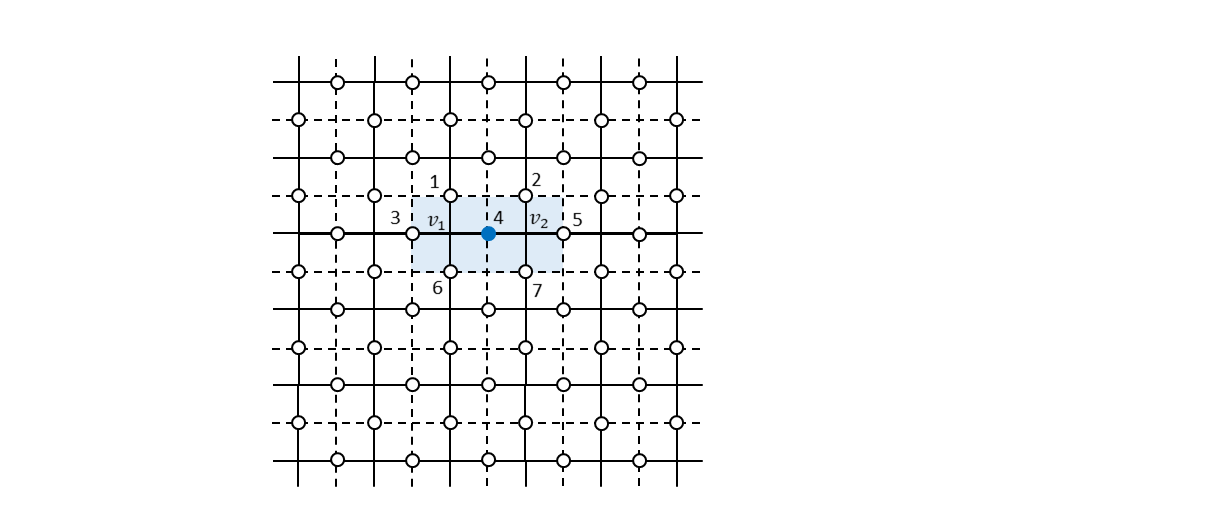
表面符号とは、平面上に量子ビットを規則正しく並べて、その上で規則正しく定義されたスタビライザー群の生成元によって規定される誤り訂正符号のことです。例えば、$n \times n$の2次元格子を考え、その辺の真ん中に量子ビットを配置することを考えます(下図左)。そして、周期的境界条件を満たしているものとします。つまり、一番上と一番下の辺は同じものであり一番左と一番右の辺は同じものだとします。一番上の辺と一番下の辺をくるっと丸めてくっつけて筒状にしてから、筒の両端にできた2つの円をぐるっと回してくっつけるとドーナツ形=トーラスが出来上がりますが、そんなイメージです。3次元のオブジェクトを図示するのは大変なので、以下では平面上に表現された格子を使って説明していきますが、頭の中ではトーラスの展開図だと思っておいてください。
スタビライザー符号を構築するには生成元が必要です。というわけで、この格子上に2種類の生成元を定義します。ひとつは「面演算子(plaquette operator)」というもので、もうひとつは「頂点演算子(star operator)」というものです(上図右)。
面演算子$A_m$は格子の各面$f_m$に対応して以下のように定義されます。
A_m = \prod_{i \in \partial f_m} Z_i \tag{1}
ここで、$\partial f_m$は$m$番目の面$f_m$の境界に相当する4つの辺を表し、$Z_i$は$i$番目の辺に配置された量子ビットに対するパウリ$Z$演算子です。上図右に示したように各面を囲む四角形としてイメージしておけば良いです。これが格子全面に敷き詰められています。
一方、頂点演算子は格子の各頂点$v_k$に対応して以下のように定義されます。
B_k = \prod_{j \in \delta v_k} X_j \tag{2}
ここで、$\delta v_k$は、$k$番目の頂点$v_k$に接続している4つの辺を表し、$X_j$は$j$番目の辺に配置された量子ビットに対するパウリ$X$演算子です。上図右に示したように各頂点を中心にした十文字としてイメージしておけば良いです。これも先程と同様に格子全面に敷き詰められています。面演算子同士、頂点演算子同士は可換ですし、頂点演算子と面演算子は重なる場合は必ず量子ビット2個を共有する形になるので可換です($X_{i}X_{j}$と$Z_{i}Z_{j}$は可換なので)。したがって、これで可換な生成元が定義できました。
さて、ここで問題です。この$n \times n$の2次元格子に量子ビット(辺)と面演算子と頂点演算子はそれぞれいくつあるでしょうか。周期的な境界条件を考慮すると、量子ビット(辺)の数は$2n^2$個、面演算子(面)の数は$n^2$個、頂点演算子(頂点)の数は$n^2$個であることがわかります。両者合わせて可換な$2n^2$個の生成元があるのですが、全部が独立というわけではありません。面演算子のすべての積は恒等演算子$I$ですし、頂点演算子のすべての積も恒等演算子$I$です1。拘束条件が2個あるので、独立な生成元の個数は$2n^2-2$ということになります。量子ビット(辺)の数は$2n^2$個だったので、この符号空間で記述することができる論理ビット数は$2n^{2}-(2n^{2}-2)=2$個ということになります。
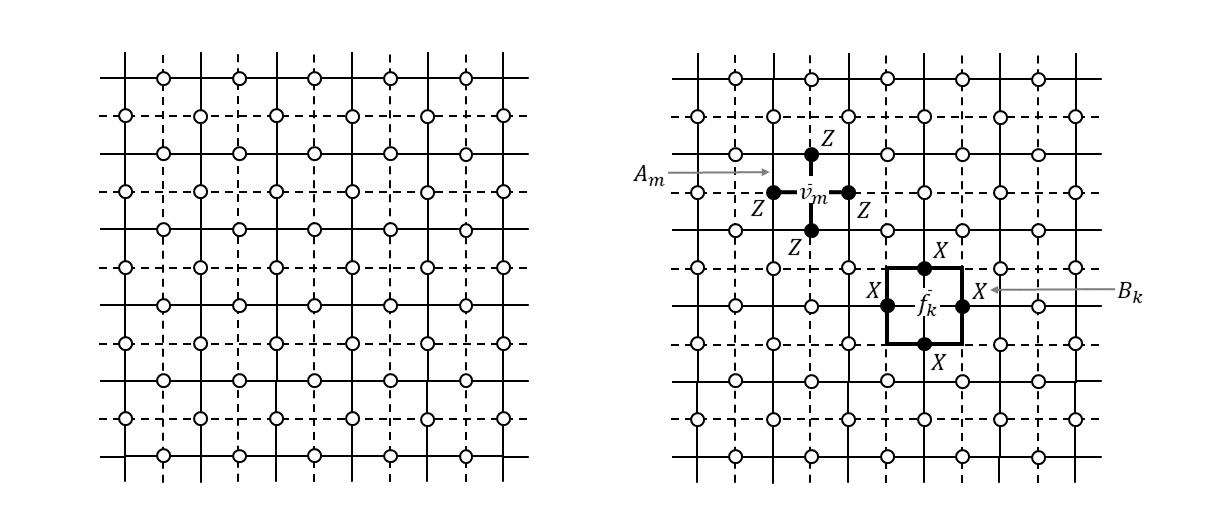
双対格子
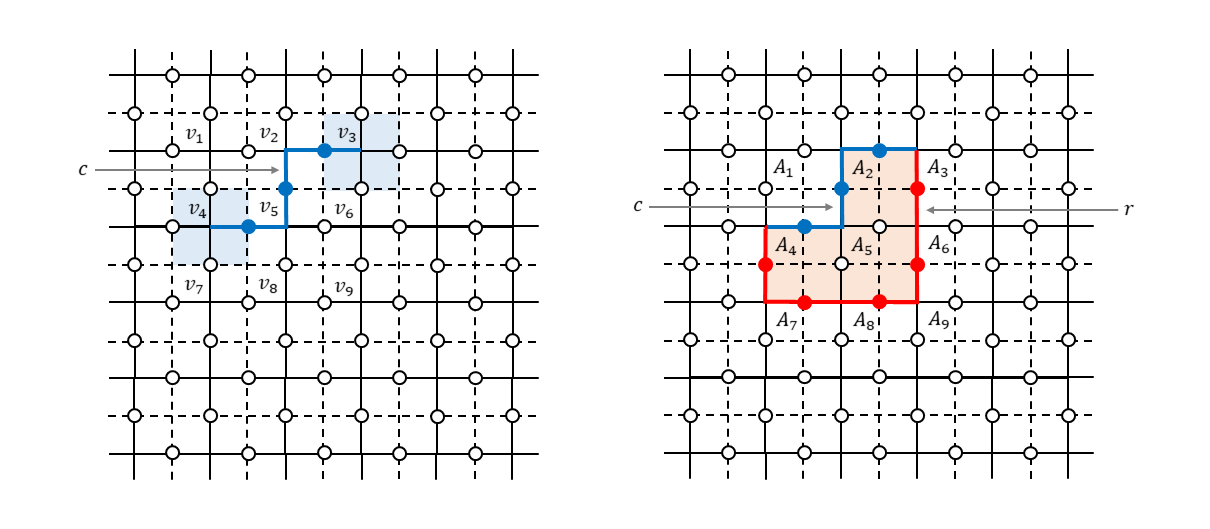
上図で示した格子は頂点同士をつないだものを辺としましたが、面同士をつないだものを辺とした別の格子を考えることもできます。つまり、面の中央に頂点をおいてそれらをつないだような格子です(下図左、破線で示されています)。このような格子のことを「双対格子(dual lattice)」と呼びます。
この双対格子を使って面演算子と頂点演算子を表現すると、不思議なことが起きます(というかちょっと考えればすぐわかると思いますが)。面演算子の形が十文字になり、頂点演算子の形が四角形となり、図形のイメージが逆転します(上図右)。
元の格子(primal lattice)の面・辺・頂点は、双対格子においては各々頂点・辺・面となりますので、生成元$A_m,B_k$は以下のように双対格子の言葉で書き直すことができます。
A_m = \prod_{i \in \delta \bar{v}_m} Z_i \tag{3}
B_k = \prod_{j \in \partial \bar{f}_k} X_j \tag{4}
ここで、$\bar{v}_m$は面$f_m$を双対格子で表したときの頂点、$\bar{f}_k$は頂点$v_k$を双対格子で表したときの面です(以降、双対格子上の実体であることを明示するため記号の上にバーをつけることにします)。なぜこのようなものをここで導入したかについては、この後の説明の中でわかりますので、一応覚えておいてください2。
自明なループ
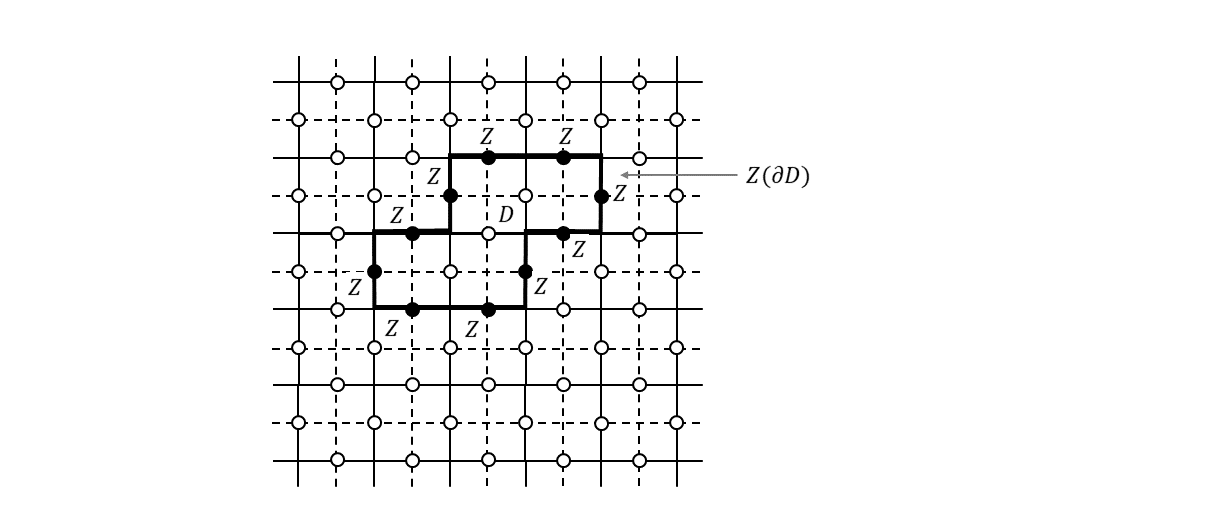
生成元が定義できたところで、格子=トーラス上で定義されるループが演算子的にどんな性質を持っているのかを考えてみます。まず、格子上の面$D$の境界$\partial D$を考えます(下図)。
このようなループのことを「自明なループ」と呼びます3。ループを構成する各辺に置いた$Z$演算子の積を$Z(\partial D)$と書くことにすると、
Z(\partial D) = \prod_{m,f_m \in D} A_{m} \tag{5}
が成り立ちます。右辺は面$D$を構成するすべての面演算子の積をとった形になっていますが、これはわかりますでしょうか。隣接した2つの面演算子は1つの$Z$演算子を共有していますので、両者の積をとると共通した辺が$I$となります。$D$に含まれる面演算子すべてで積をとると$D$の境界以外のすべての辺は$I$となり、結局境界$\partial D$の上にある$Z$演算子だけが残ることになります。式(5)から明らかなように、この演算子$Z(\partial D)$は、すべての生成元と可換で、かつ、スタビライザー群の要素になっています($A_{m}$の積なので)。
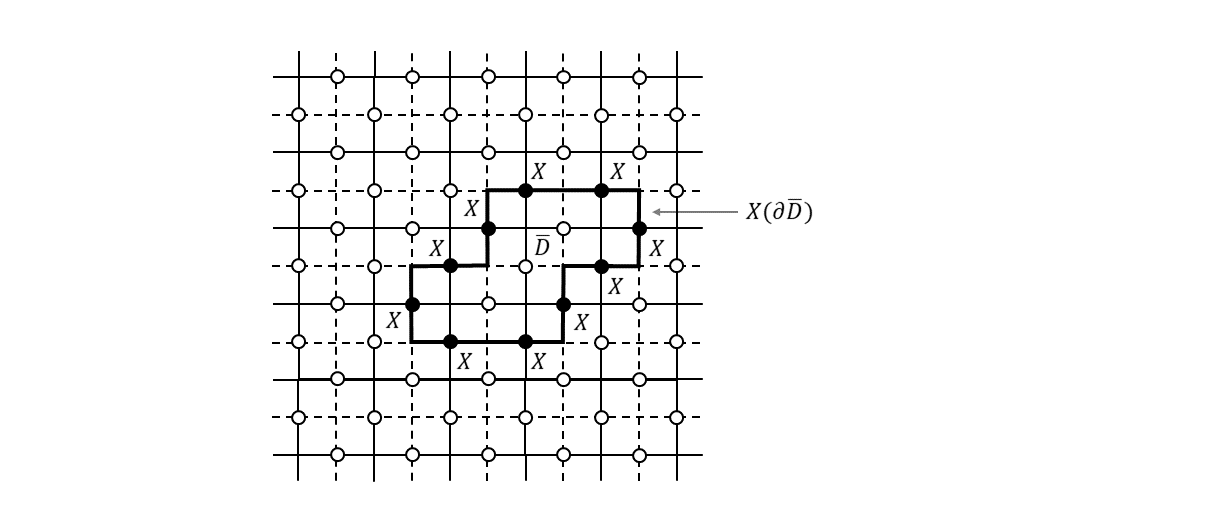
次に、双対格子上に定義された面$\bar{D}$の境界$\partial \bar{D}$を考えます(下図)。
双対格子上のループを構成する各辺に置いた$X$演算子の積を$X(\partial \bar{D})$と書くことにすると、
X(\partial \bar{D}) = \prod_{k,\bar{f}_k \in \bar{D}} B_{k} \tag{6}
が成り立ちます。先ほどと同様に面を構成するすべての面演算子(元の格子においては頂点演算子だったもの)の積をとると境界上の$X$演算子だけが残る形になります。式(6)から明らかなように、この演算子$X(\partial \bar{D}))$も、すべての生成元と可換で、かつ、スタビライザー群の要素です。
というわけで、元の格子の自明なループ上に配置された$Z$演算子の積、および双対格子の自明なループ上に配置された$X$演算子の積はスタビライザー群の要素であり、これを符号状態に適用しても符号状態は不変になります。
非自明なループ
次に、自明でないループ=非自明なループの上に配置された$Z$演算子と$X$演算子がどんな性質を持つのかを見ていきます。
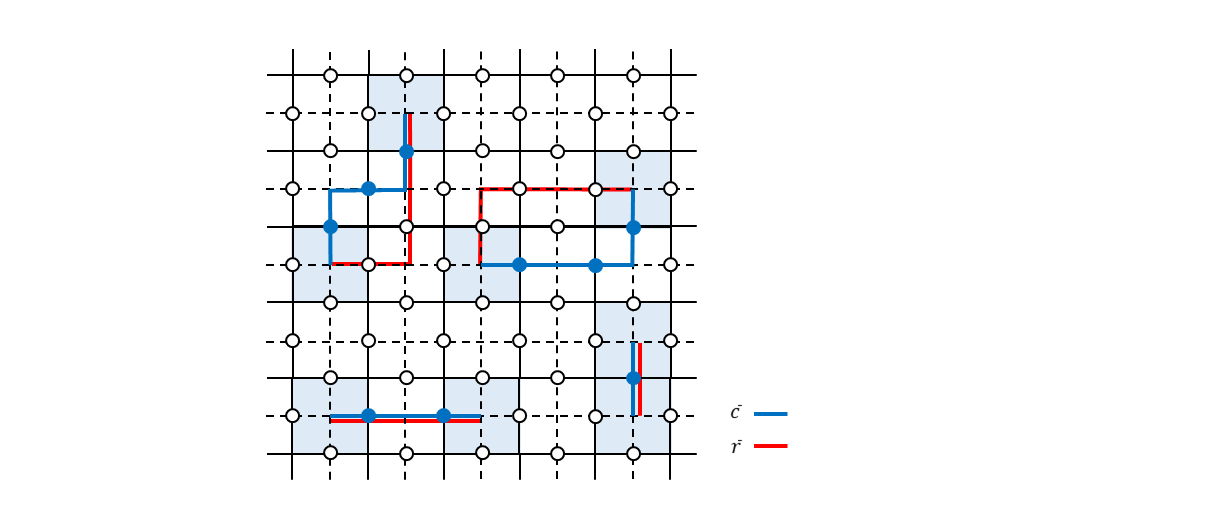
上図に$l_1$と書かれている直線がありますが、これは周期的境界条件を前提とするとトーラスに巻き付くループになります。ループなのですが連続的な変形で一点に収縮させることができないので非自明なループです。この各辺に$Z$演算子を並べて積をとったものを、
\tilde{Z}_1 = Z(l_1) \tag{7}
と書くことにします。そうすると、この演算子と生成元たちは可換になります。面演算子に含まれるのは$Z$演算子だけなので当然ですし、頂点演算子の方は$l_1$と重なる辺は必ず2個ですので可換になります4。可換なのですが、これはスタビライザー群の要素ではありません。つまり生成元の積の形で表すことができません。嘘だと思ったら頑張ってやってみてください。例えば、$l_1$上に並んだ$Z$演算子の積をつくりたいため$l_1$に隣接する形に面演算子を並べたとしましょう。でも、これらの積によってできあがるのは$Z(l_1)$ともうひとつ別の非自明なループ上に配置された$Z$演算子です。
すべての生成元と可換でありスタビライザー群の要素ではない演算子というのは一体何でしょうか。答えは論理演算子です。ん?となったかもしれないので、一応説明しておきます。スタビライザー群$S$を独立な生成元を使って、
S = < g_1, g_2, \cdots g_{n-k} > \tag{8}
のように書き、スタビライザー状態を$\ket{\psi}$とします。すべての生成元$g_i$と可換な演算子$g \notin S$を持ってくると、
g \ket{\psi} = g g_{i} \ket{\psi} = g_{i} g \ket{\psi} \tag{9}
が成り立つので、$g\ket{\psi}$は$g_i$の固有値$+1$に対応した固有空間たちの積空間上の状態(同時固有状態)です。つまり、符号空間上の状態です。が、$g\ket{\psi} = \ket{\psi}$は成り立ちません($g \notin S$なので)。したがって、$g$は符号空間からはみ出すことなく論理状態だけを変える演算子、つまり論理演算子ということになります。
いま、式(7)で定義された$\tilde{Z}_1$を1番目の論理ビットに対する論理$Z$演算子だとします5。
では、1番目の論理ビットに対する$X$演算子はどのように定義すれば良いでしょうか。
\tilde{X}_1 = X(\bar{l}_1) \tag{10}
とすれば、すべての生成元と可換で、$\tilde{X}_1 \tilde{Z}_1 \tilde{X}_1 = -\tilde{Z}_1$を満たすようにできるので、これでOKです。
さらに、2番目の論理ビットに対する$Z$演算子は、
\tilde{Z}_2 = Z(l_2) \tag{11}
とすれば良いです。$\tilde{Z}_1$を定義する際に縦方向にぐるっと回る非自明ループを使ったので、横方向にぐるっと回る非自明ループを使います6。
2番目の論理ビットに対する$X$演算子は、すべての生成元と可換で、$\tilde{Z}_2$と反可換になるように、
\tilde{X}_2 = X(\bar{l}_2) \tag{12}
とすれば良いです。これですべての基本論理演算子が出揃いました。繰り返しますが、上図で示した4つのループはひとつの例です。トポロジー的に別の非自明ループを元の格子と双対格子で各々用意すれば、それによって2つの論理ビットに対する$Z$演算子と$X$演算子を定義できます7。
誤り訂正
符号空間と基本的な論理演算子が定義できたので、この符号を使ってどのように誤り訂正が実現できるかを説明します。
ビット反転エラー
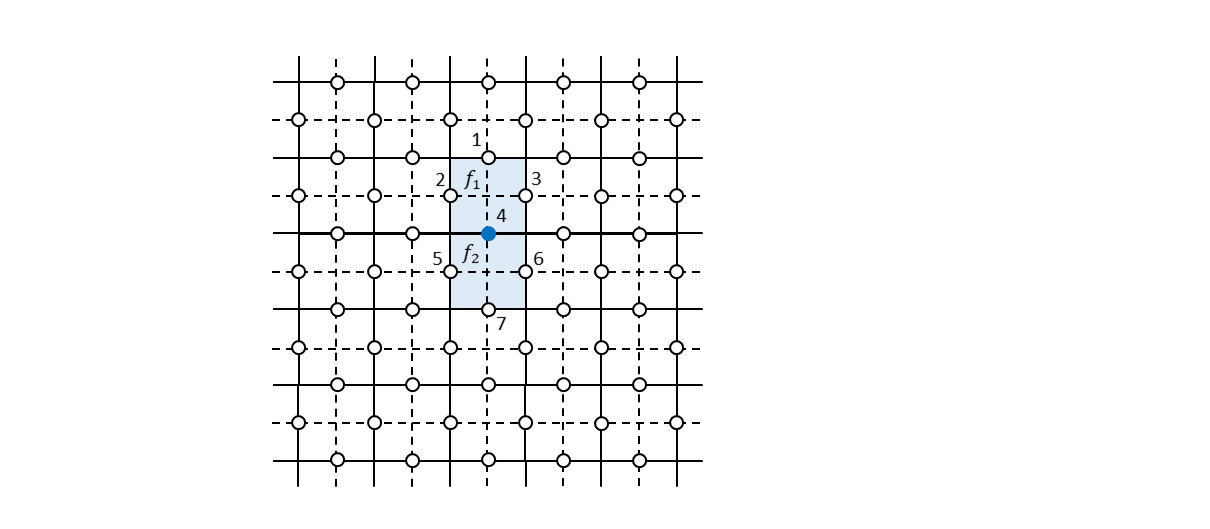
まず、ビット反転エラーがどこか1つのビットに発生した場合にどのように誤りビットを特定できるかについて見ていきます。例えば、下図で番号4のビットにビット反転エラーが発生したとします。
この場合、すべての生成元を測定すると上図の$f_1$と$f_2$に対応した面演算子$Z_{1} Z_{2} Z_{3} Z_{4}$および$Z_{4} Z_{5} Z_{6} Z_{7}$のみが測定値$-1$を出力します。元の論理状態を$\ket{\psi_{L}}$とすると、
\begin{align}
Z_{1} Z_{2} Z_{3} Z_{4} (X_{4} \ket{\psi_{L}}) &= - X_{4} (Z_{1} Z_{2} Z_{3} Z_{4} \ket{\psi_{L}}) = -X_{4} \ket{\psi_{L}} \\
Z_{4} Z_{5} Z_{6} Z_{7} (X_{4} \ket{\psi_{L}}) &= - X_{4} (Z_{4} Z_{5} Z_{6} Z_{7} \ket{\psi_{L}}) = -X_{4} \ket{\psi_{L}} \tag{13}
\end{align}
となることから、測定値は$100%$の確率で$-1$になることがわかります。したがって、各生成元をシンドローム測定して$-1$を出したものが面演算子だった場合、ビット反転エラーがあったということになり、その場所は面演算子同士が接しているところであると特定することができます。特定されたビットに再度ビット反転を施すことで元の状態に戻すことができます。
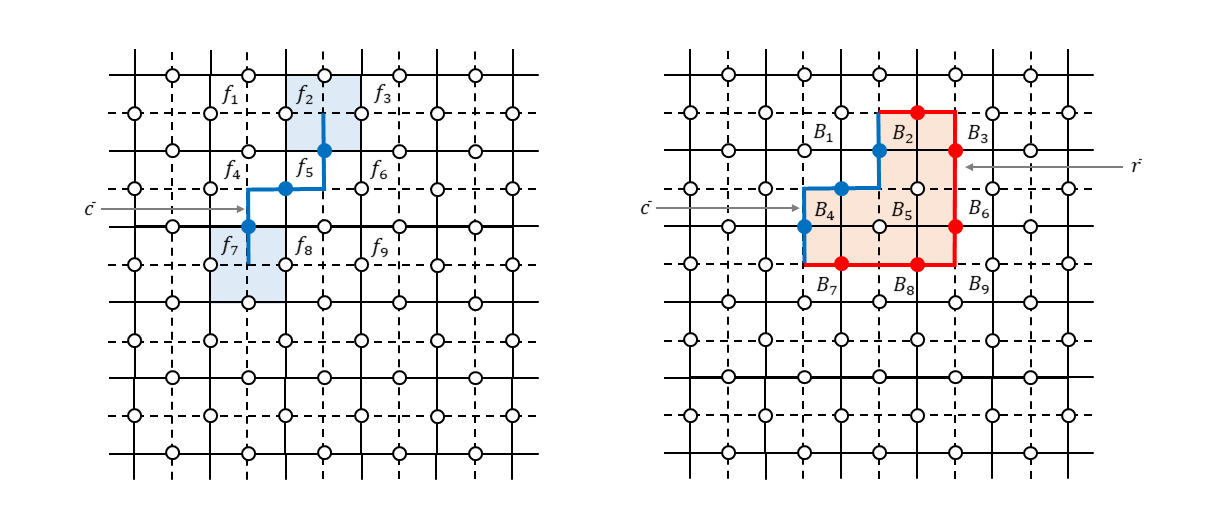
では、2つ以上のビットにビット反転エラーがあったときはどうでしょうか。例えば、下図左のように青で示した3つのビットにエラーがあった場合について考えます。
生成元を測定して$-1$を出力するのは面$f_2$と面$f_7$に対応した面演算子だけです。面$f_4$と面$f_5$を構成するビットにもエラーが発生しているのですが各々2ビット同時にビット反転しているため測定値としては$+1$になってしまいます。このように隣接している面に属するビットにエラーがあった場合、双対格子で見るとつながったチェーンのように見えるので「エラーチェーン」と言ったりしますが(青の線で示しました)、このチェーンの端点に相当する面演算子だけがシンドローム測定で反応します(測定値が$-1$になります。薄い青で塗りつぶした部分です)。この端点の情報から何とか全体のエラーチェーンを復元して誤り訂正しないといけません。いわゆる不良設定問題?というわけで、頑張ったとしても何となく確率的にしか成功しない手法なのね?という雰囲気になったかもしれません。が、ご安心ください。ここが表面符号のとてもエライところだと思うのですが、実はエラーチェーンの推定がある程度外れていても大丈夫なのです。なぜ大丈夫なのかを説明します。
上図右を見てください。本当のエラーチェーンが$\bar{c}$だったとします(青の線で示しました)。それに対して推定したエラーチェーンが$\bar{r}$だったとします(赤の線で示しました)。このとき本当のエラーは$X(\bar{c})$なのですが、推定したエラーは$X(\bar{r})$です。$X(\bar{c})$と$X(\bar{r})$とは図からわかるように頂点演算子$B_2,B_4,B_5$(薄いオレンジ色で塗りつぶした部分です)の積を演算することで互いに移行することができます。つまり、
X(\bar{c}) = B_{2} B_{4} B_{5} X(\bar{r}) \tag{14}
です。したがって、エラーが$X(\bar{r})$だと思って回復処理をしたとしても、
\begin{align}
X(\bar{r}) X(\bar{c}) \ket{\psi_{L}} &= X(\bar{r}) B_{2} B_{4} B_{5} X(\bar{r}) \ket{\psi_{L}} \\
&= X(\bar{r}) X(\bar{r}) B_{2} B_{4} B_{5} \ket{\psi_{L}} \\
&= B_{2} B_{4} B_{5} \ket{\psi_{L}} = \ket{\psi_{L}} \tag{15}
\end{align}
となり、結局元の状態に戻ったことになります8。というわけで、上図右のように本当のエラーチェーンと連続変形で移ることができるエラーチェーンが推定できていれば、問題なく元の符号状態を回復することができます。
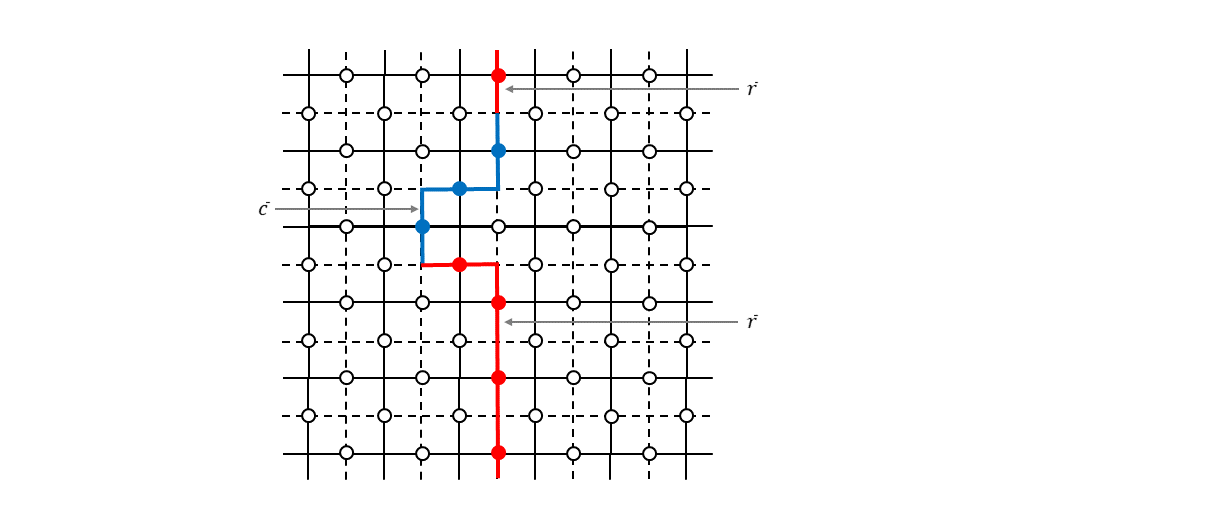
が、下図のように本当のエラーチェーンと連続変形できないようにエラーチェーンを推定すると回復処理は失敗することになります。
位相反転エラー
次に、位相反転エラーがどこか1つのビットに発生した場合について考えます。下図のように4番目のビットに位相反転エラーが発生したとします。
この場合、すべての生成元を測定すると上図の$v_1$と$v_2$に対応した頂点演算子$X_{1} X_{3} X_{4} X_{6}$および$X_{2} X_{4} X_{5} X_{7}$のみが測定値$-1$を出力します。元の論理状態を$\ket{\psi_{L}}$とすると、
\begin{align}
X_{1} X_{3} X_{4} X_{6} (Z_{4} \ket{\psi_{L}}) &= - Z_{4} (X_{1} X_{3} X_{4} X_{6} \ket{\psi_{L}}) = -Z_{4} \ket{\psi_{L}} \\
X_{2} X_{4} X_{5} X_{7} (Z_{4} \ket{\psi_{L}}) &= - Z_{4} (X_{2} X_{4} X_{5} X_{7} \ket{\psi_{L}}) = -Z_{4} \ket{\psi_{L}} \tag{16}
\end{align}
となることから、測定値は$100%$の確率で$-1$になることがわかります。したがって、各生成元をシンドローム測定して$-1$を出したものが頂点演算子だった場合、位相反転エラーがあったということになり、その場所は頂点演算子同士が接しているところであると特定することができます。特定されたビットに再度位相反転を施すことで元の状態に戻すことができます。
では、2つ以上のビットに位相反転エラーがあったときはどうでしょうか。例えば、下図左のように青で示した3つのビットにエラーがあった場合について考えます。
生成元を測定して$-1$を出力するのは頂点$v_3$と頂点$v_4$に対応した頂点演算子だけです(薄い青で塗りつぶした部分です)。頂点$v_2$と頂点$v_5$を構成するビットにエラーが発生しているのですが各々2ビット同時に位相反転しているため測定値としては$+1$になってしまいます。この場合、頂点$v_3,v_2,v_5,v_4$をつないだエラーチェーンを推定する必要があります。が、先程と同様に、推定したエラーチェーン$r$が本当のエラーチェーン$c$から連続変形できるものになっていれば、推定したものに基づいて作成した$Z(r)$を適用することで元の論理状態に回復させることができます。回復が失敗するのは推定したチェーンが本当のチェーンから連続変形できない場合です。
エラーチェーンの推定
いま見てきたようにエラーチェーンの推定が多少外れていたとしても回復できるのですが、推定したエラーチェーンが本当のエラーチェーンと連続変形によって移行できないものになっていると誤り訂正は失敗します。なるべく失敗しないようにしたいわけですが、どのように推定するのが一番良いでしょうか、ということについて考えてみます。
いま、エラーチェーン$\bar{c}$上にビット反転エラー$X(\bar{c})$が発生したとします(位相反転エラーの場合も同様の議論が成り立つので、ここではビット反転エラーのみについて考えます)。ここで、エラーチェーン$\bar{c}$はつながった1本のチェーンであるとは限りません。複数のチェーンをひっくるめて$\bar{c}$と表しているのだとイメージしておいてください(下図の青線)。
このようなエラーが発生する確率$p(\bar{c})$は、
p(\bar{c}) = (1-p)^{|E|} \prod_{i \in E} \Bigl(\frac{p}{1-p} \Bigr)^{z_i} \tag{17}
と表せます。ここで、$|E|$は辺の総数、$z_i$は$i$番目の辺が$\bar{c}$に含まれる場合$1$、そうでない場合$0$という値をとるバイナリ値とします9。
シンドローム測定の結果$\bar{c}$の境界$\partial \bar{c}$という端点が得られたときに、一番もっともらしいエラーチェーンは、$\partial \bar{c}$を得たという条件のもとで条件付き確率$p(\bar{c}^{\prime}|\partial \bar{c})$が最大になる$\bar{c}^{\prime}$であると考えるのが良さそうです。つまり、
\bar{r} = \arg \max_{\bar{c}^{\prime}} p(\bar{c}^{\prime}|\partial \bar{c}) \tag{18}
によってエラーチェーンを推定するのが良さそうです。ここで、$p(\bar{c}^{\prime}|\partial \bar{c})$は、
p(\bar{c}^{\prime}|\partial \bar{c}) \propto (1-p)^{|E|} \prod_{i \in E} \Bigl( \frac{p}{1-p} \Bigr)^{z_{i}^{\prime}} \Bigr|_{\partial \bar{c}^{\prime} = \partial \bar{c}} \tag{19}
と表すことができます。このとき、$z_{i}^{\prime}$は$i$番目の辺が$\bar{c}^{\prime}$に含まれる場合$1$、そうでない場合$0$という値をとるバイナリ値であるとしているので、式(19)を最大にするバイナリ系列$\{ z_{i}^{\prime} \}$を求めれば、式(18)の$\bar{r}$がわかったことになります。式(19)をじっと眺めればわかる通り、これを最大にするためにはバイナリ系列$\{ z_{i}^{\prime} \}$の中に含まれる$1$の個数が最小になるようにすれば良いです。言い方を変えると、すべての端点を距離が最小になるようにつなげば良いということになります(下図の赤線)。このようなグラフ最適化アルゴリズムは「最小重み完全マッチングアルゴリズム(minimum weight perfect matching algorithm)」と呼ばれており、多項式ステップで解けるアルゴリズムが知られています(が、よくわかっていないので、説明省略します、汗)。
エラー確率と訂正失敗率
一般に、符号化する際のビット数を大きくして冗長度を上げると、性能の良い(訂正失敗率が低い)誤り訂正が実現できますが、その前提としてビットあたりのエラー確率がある閾値以下になっていることが必要です。
例えば、1ビットを$N$ビットで冗長化する古典反復符号を考えると、$N$ビットのうち半数を越えないエラーであれば多数決をとることで完全復元できます。ざっくり言うと、ビットあたりのエラー確率が閾値$1/2$よりも小さければだいたい復元できます。ここで「だいたい」と言ったのは、伝送したい1つの信号を構成する半数以上のビットにエラーが紛れ込む場合も確率的にあり得るのでその場合復元は失敗します、という意味です。が、$N$の値を十分に大きくとることができれば、この失敗率を限りなくゼロにすることができます。もちろん、このときエラー確率が閾値($1/2$)よりも小さい場合という前提条件は必須になります。エラー確率が閾値よりも大きかった場合は、$N$の値を大きくすると逆効果です。大きくすればするほど確実に復元が失敗する方向に向かいます10。
量子誤り訂正符号の場合も同様で、誤り訂正が効果を発揮するか否かは、ビットあたりのエラー確率がある閾値以下になっていることが必要です。ある閾値以下になっていれば、$N$を十分に大きくすれば訂正失敗率が限りなくゼロに近くなります。が、逆にエラー確率が閾値以上になっていると、$N$を大きくすると訂正失敗率はかえって大きくなります。
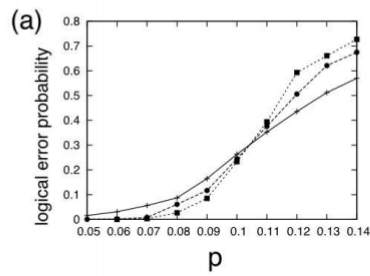
では、表面符号の場合この閾値はどの程度になるでしょうか。数値シミュレーションした結果が参考文献3に掲載されているので、以下に引用します。
ここで、横軸がビットごとのエラー確率、縦軸が訂正失敗率を表していて、実線が$n=10$、破線が$n=20$、点線が$n=30$の訂正失敗率をプロットしたものになります(いま$n \times n$の格子を考えています)。このS字カーブの変曲点からエラー確率の閾値は$10.3%$程度と求められているそうです。ちなみに、このシミュレーションは「最小重み完全マッチングアルゴリズム」でエラーチェーンの推定をした場合です。
表面符号は、複数のエラーチェーンのパターンに対して同じシンドローム測定の結果が得られる縮退符号なので、実は最小距離が最適とは限りません。同じ訂正結果を与える合計確率が最大になるようにしたものが最適な復号なので、そうした場合この閾値は$10.9%$程度になるそうです。
また、正方格子ではビット反転エラーも位相反転エラーも同じエラー確率の閾値を持つのですが、蜂の巣形やカゴメ形などに格子形状を変えるとビット反転エラーと位相反転エラーの閾値は非対称になります。実際の物理系においてはビット反転よりも位相反転の方が大きい場合が多いため、そのような想定でのシミュレーションも行われているようです(詳細は参考文献3をご参照ください)。
いま説明した$10%$程度のエラー閾値というのは表面符号で符号状態が保持・伝送されることに伴って発生するエラーに関するものです。実際の量子計算においては初期状態準備、論理演算、測定に伴うエラーも考慮に入れないといけません。それらすべてを合わせてフォールトトレラントな量子計算を実現するためには、各部品あたりのエラー率はだいたい$1%$程度必要と見積もられているようです。前回の記事で説明したようにSteane符号のようなCSS符号をベースとした連結符号を想定すると$10^{-4}=0.01%$程度以下の閾値11が必要ということだったので、これは大きな進展です。「はじめに」で「希望の光」と言っていたのはこのことです。
動作確認
それでは、量子計算シミュレータqlazyを使って、$3 \times 3$の格子上で表面符号を構成し誤り訂正が正しく実行できることを確認してみます。
実装
全体のPythonコードを示します。
【2021.9.5追記】qlazy最新版でのソースコードはここに置いてあります。
from qlazypy import QState
Lattice = [{'edge': 0, 'faces':[0, 6], 'vertices':[0, 1]},
{'edge': 1, 'faces':[1, 7], 'vertices':[1, 2]},
{'edge': 2, 'faces':[2, 8], 'vertices':[0, 2]},
{'edge': 3, 'faces':[0, 2], 'vertices':[0, 3]},
{'edge': 4, 'faces':[0, 1], 'vertices':[1, 4]},
{'edge': 5, 'faces':[1, 2], 'vertices':[2, 5]},
{'edge': 6, 'faces':[0, 3], 'vertices':[3, 4]},
{'edge': 7, 'faces':[1, 4], 'vertices':[4, 5]},
{'edge': 8, 'faces':[2, 5], 'vertices':[3, 5]},
{'edge': 9, 'faces':[3, 5], 'vertices':[3, 6]},
{'edge':10, 'faces':[3, 4], 'vertices':[4, 7]},
{'edge':11, 'faces':[4, 5], 'vertices':[5, 8]},
{'edge':12, 'faces':[3, 6], 'vertices':[6, 7]},
{'edge':13, 'faces':[4, 7], 'vertices':[7, 8]},
{'edge':14, 'faces':[5, 8], 'vertices':[6, 8]},
{'edge':15, 'faces':[6, 8], 'vertices':[0, 6]},
{'edge':16, 'faces':[6, 7], 'vertices':[1, 7]},
{'edge':17, 'faces':[7, 8], 'vertices':[2, 8]}]
F_OPERATORS = [{'face':0, 'edges':[ 0, 3, 4, 6]},
{'face':1, 'edges':[ 1, 4, 5, 7]},
{'face':2, 'edges':[ 2, 3, 5, 8]},
{'face':3, 'edges':[ 6, 9, 10, 12]},
{'face':4, 'edges':[ 7, 10, 11, 13]},
{'face':5, 'edges':[ 8, 9, 11, 14]},
{'face':6, 'edges':[ 0, 12, 15, 16]},
{'face':7, 'edges':[ 1, 13, 16, 17]},
{'face':8, 'edges':[ 2, 14, 15, 17]}]
V_OPERATORS = [{'vertex':0, 'edges':[ 0, 2, 3, 15]},
{'vertex':1, 'edges':[ 0, 1, 4, 16]},
{'vertex':2, 'edges':[ 1, 2, 5, 17]},
{'vertex':3, 'edges':[ 3, 6, 8, 9]},
{'vertex':4, 'edges':[ 4, 6, 7, 10]},
{'vertex':5, 'edges':[ 5, 7, 8, 11]},
{'vertex':6, 'edges':[ 9, 12, 14, 15]},
{'vertex':7, 'edges':[10, 12, 13, 16]},
{'vertex':8, 'edges':[11, 13, 14, 17]}]
LZ_OPERATORS = [{'logical_qid':0, 'edges':[0, 1, 2]},
{'logical_qid':1, 'edges':[3, 9, 15]}]
LX_OPERATORS = [{'logical_qid':0, 'edges':[0, 6, 12]},
{'logical_qid':1, 'edges':[3, 4, 5]}]
def make_logical_zero():
qs = QState(19) # data:18 + ancilla:1
mvals = [0, 0, 0, 0, 0, 0, 0, 0, 0] # measured values of 9 plaquette operators
for vop in V_OPERATORS: # measure and get measured values of 9 star operators
qid = vop['edges']
qs.h(18).cx(18,qid[0]).cx(18,qid[1]).cx(18,qid[2]).cx(18,qid[3]).h(18)
mvals.append(int(qs.m(qid=[18]).last))
qs.reset(qid=[18])
return qs, mvals
def measure_syndrome(qs, mvals):
syn = []
for fop in F_OPERATORS: # plaquette operators
qid = fop['edges']
qs.h(18).cz(18,qid[0]).cz(18,qid[1]).cz(18,qid[2]).cz(18,qid[3]).h(18)
syn.append(int(qs.m(qid=[18]).last))
qs.reset(qid=[18])
for vop in V_OPERATORS: # star operators
qid = vop['edges']
qs.h(18).cx(18,qid[0]).cx(18,qid[1]).cx(18,qid[2]).cx(18,qid[3]).h(18)
syn.append(int(qs.m(qid=[18]).last))
qs.reset(qid=[18])
for i in range(len(syn)): syn[i] = syn[i]^mvals[i]
return syn
def get_error_chain(syn):
face_id = [i for i,v in enumerate(syn) if i < 9 and v == 1]
vertex_id = [i-9 for i,v in enumerate(syn) if i >= 9 and v == 1]
e_chn = []
if face_id != []: # chain type: X
for lat in Lattice:
if lat['faces'][0] == face_id[0] and lat['faces'][1] == face_id[1]:
e_chn.append({'type':'X', 'qid':[lat['edge']]})
break
if vertex_id != []: # chain type: Z
for lat in Lattice:
if lat['vertices'][0] == vertex_id[0] and lat['vertices'][1] == vertex_id[1]:
e_chn.append({'type':'Z', 'qid':[lat['edge']]})
break
return e_chn
def error_correction(qs, e_chn):
for c in e_chn:
if c['type'] == 'X': [qs.x(i) for i in c['qid']]
if c['type'] == 'Z': [qs.z(i) for i in c['qid']]
def Lz(self, q):
[self.z(i) for i in LZ_OPERATORS[q]['edges']]
return self
def Lx(self, q):
[self.x(i) for i in LX_OPERATORS[q]['edges']]
return self
if __name__ == '__main__':
QState.add_methods(Lz, Lx)
print("* initial state: logical |11>")
qs_ini, mval_list = make_logical_zero() # logical |00>
qs_ini.Lx(0).Lx(1) # logical |00> -> |11>
qs_fin = qs_ini.clone() # for evaluating later
print("* add noise")
qs_fin.x(7) # bit flip error at #7
# qs_fin.z(7).x(7) # bit and phase flip error at #7
syndrome = measure_syndrome(qs_fin, mval_list)
err_chain = get_error_chain(syndrome)
print("* syndrome measurement:", syndrome)
print("* error chain:", err_chain)
error_correction(qs_fin, err_chain)
print("* fidelity after error correction:", qs_fin.fidelity(qs_ini))
QState.free_all(qs_ini, qs_fin)
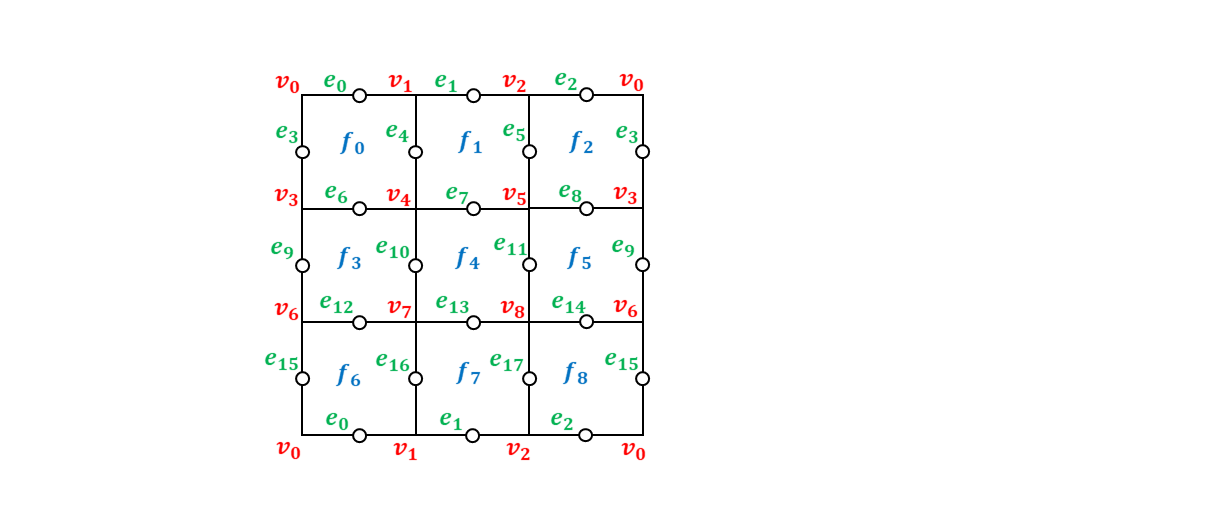
まず、格子上の面と辺と頂点番号を以下のように決めました。ここで、$v_i$が面、$e_i$が辺、$f_i$が頂点を表しています。
プログラム冒頭に記載したグローバル変数Lattice,F_OPERATORS,V_OPERATORS,LZ_OPERATORS,LX_OPERATORSはこの面・辺・頂点を前提にしたときのグラフ構造や生成元や論理演算子を定義するためのデータです。Latticeは各辺に接続している面番号と頂点番号からなる辞書のリストです。これで格子のグラフ構造が漏れなく記述できることになります。F_OPERATORSは各面の境界を構成する辺番号からなる辞書のリストであり、これで$9$個の面演算子を定義します。V_OPERATORSは各頂点に接続する辺番号からなる辞書のリストであり、これで$9$個の頂点演算子を定義します。LZ_OPERATORSは2つの論理$Z$演算子を定義するためのもので、$0$番目の論理$Z$が$Z_{0} Z_{1} Z_{2}$、$1$番目の論理$Z$が$Z_{3} Z_{9} Z_{15}$であることを表しています。LX_OPERATORSは2つの論理$X$演算子を定義するためのもので、$0$番目の論理$X$が$X_{0} X_{6} X_{12}$、$1$番目の論理$X$が$X_{3} X_{4} X_{5}$であることを表しています。
この構成を前提に、main処理部の各部分を順に見ていきます。
qs_ini, mval_list = make_logical_zero() # logical |00>
で、論理ゼロ状態を作成します。関数make_logical_zeroの中身は以下です。
def make_logical_zero():
qs = QState(19) # data:18 + ancilla:1
mvals = [0, 0, 0, 0, 0, 0, 0, 0, 0] # measured values of 9 plaquette operators
for vop in V_OPERATORS: # measure and get measured values of 9 star operators
qid = vop['edges']
qs.h(18).cx(18,qid[0]).cx(18,qid[1]).cx(18,qid[2]).cx(18,qid[3]).h(18)
mvals.append(int(qs.m(qid=[18]).last))
qs.reset(qid=[18])
return qs, mvals
今回、必要なデータビットは18ビット(0番-17番)ですが、初期状態作成やシンドローム測定のため補助ビットを1ビット追加して(18番)、合計19ビット用意します。補助ビットはもっと沢山必要なのでは?と思われるかもしれませんが、何度もリセットしながら使い回すので大丈夫です。
最初に物理的なゼロ状態をQState(19)で作っておいてforループ内で生成元を間接測定します。頂点演算子の分しか測定していないように見えますが、これはこれで良いのです。最初に用意するのが物理的なゼロ状態、すなわち面演算子の固有値+1に対応した同時固有状態なので面演算子を測定しても状態は変わりません。また面演算子と頂点演算子は可換なのではじめに面演算子を測定しても良いです。という事情があり、ここは頂点演算子の測定だけでOKです。
で、9個ある頂点演算子を順に測定するのですが、測定結果が+1(測定値の指標としては0)だった場合はこのまま次の頂点演算子の測定に移れば良いですが、測定値が-1(測定値の指標としては1)だったときが問題です。固有値をひっくり返す演算子を用意して演算するやり方もありますが、ここではそれを端折ります。つまり、スルーします。が、測定値(の指標)は記録しておきます。すべての生成元の固有値+1に対する同時固有状態は得られませんが、何番目の生成元を測定したら測定値が-1になるべきなのかはわかるので、これでシンドローム測定は可能です。固有値が-1の生成元を測定する場合、シンドローム測定値の解釈を逆にすれば良いだけです。上の関数でmvalsというリスト変数に測定値(の指標)を格納するようにしています。18個の要素があるのですが、面演算子については絶対0なので、有無を言わさず最初に9個の0からなるリストを用意して、頂点演算子を測定するたびにその結果をmvalsにappendしていきます。最後に量子状態qsとmvalsをリターンします。
main処理部に戻ります。
qs_ini.Lx(0).Lx(1) # logical |00> -> |11>
で、2つの論理ビットに対して論理$X$を施すことで論理状態$\ket{1_{L} 1_{L}}$を作成します($\ket{0_{L} 0_{L}}$から出発しても良かったのですが、論理$X$演算子を使ってみたかったので出発点を$\ket{1_{L} 1_{L}}$にしてみました)。論理$X$演算子は、
def Lx(self, q):
[self.x(i) for i in LX_OPERATORS[q]['edges']]
return self
のように定義されています。見ての通りですので、説明省略します。
qs_fin = qs_ini.clone() # for evaluating later
で、最後に誤り訂正結果を評価するための状態複製を行います。これで初期状態が作成できたことになります。
次に、
qs_fin.x(7) # bit flip error at #7
で、7番目のビットにビット反転エラーを加えます(何でも良いので、適当に決めました)。
syndrome = measure_syndrome(qs_fin, mval_list)
で、シンドローム測定をしてエラービットとエラーの種類を特定します。関数measure_syndromeの中身は以下です。
def measure_syndrome(qs, mvals):
syn = []
for fop in F_OPERATORS: # plaquette operators
qid = fop['edges']
qs.h(18).cz(18,qid[0]).cz(18,qid[1]).cz(18,qid[2]).cz(18,qid[3]).h(18)
syn.append(int(qs.m(qid=[18]).last))
qs.reset(qid=[18])
for vop in V_OPERATORS: # star operators
qid = vop['edges']
qs.h(18).cx(18,qid[0]).cx(18,qid[1]).cx(18,qid[2]).cx(18,qid[3]).h(18)
syn.append(int(qs.m(qid=[18]).last))
qs.reset(qid=[18])
for i in range(len(syn)): syn[i] = syn[i]^mvals[i]
return syn
面演算子と頂点演算子を順に測定しながら測定結果をリストに格納していきます。これがシンドローム値になるのですが、先程説明したように固有値-1(測定指標が1)が正常値になっている生成元もありますので、その場合解釈を逆転させる必要があります。初期状態生成時に記録した測定値リストmvalsの値に応じて、
for i in range(len(syn)): syn[i] = syn[i]^mvals[i]
のようにシンドローム値を逆転させます。この結果を正しいシンドローム値としてリターンします。
main処理部に戻ります。
err_chain = get_error_chain(syndrome)
で、エラーチェーンを推定します。$3 \times 3$の格子では1ビットの誤りしか訂正できないので簡単です。関数get_error_chainの中身は以下です。
def get_error_chain(syn):
face_id = [i for i,v in enumerate(syn) if i < 9 and v == 1]
vertex_id = [i-9 for i,v in enumerate(syn) if i >= 9 and v == 1]
e_chn = []
if face_id != []: # chain type: X
for lat in Lattice:
if lat['faces'][0] == face_id[0] and lat['faces'][1] == face_id[1]:
e_chn.append({'type':'X', 'qid':[lat['edge']]})
break
if vertex_id != []: # chain type: Z
for lat in Lattice:
if lat['vertices'][0] == vertex_id[0] and lat['vertices'][1] == vertex_id[1]:
e_chn.append({'type':'Z', 'qid':[lat['edge']]})
break
return e_chn
シンドロームの値が1になっている場所から面演算子の番号face_idと頂点演算子の番号vertex_idを特定します。特定した面演算子から対応する面の境界を構成する辺の番号がわかるので、その共通する辺の番号がビット反転エラーがあったビット番号になります。また、特定した頂点演算子から対応する頂点に接続する辺の番号がわかるので、その共通する辺の番号が位相反転エラーがあったビット番号になります。このようにして、エラーチェーンを構成するビット番号とエラーの種類がわかります。それを辞書リストe_chnに格納して、リターンします。
main処理部に戻ります。いま得られたエラーチェーンから、
error_correction(qs_fin, err_chain)
で、元の状態を復元します。関数error_correctionの中身は以下です。
def error_correction(qs, e_chn):
for c in e_chn:
if c['type'] == 'X': [qs.x(i) for i in c['qid']]
if c['type'] == 'Z': [qs.z(i) for i in c['qid']]
見た通りの処理です(説明略)。これで誤り訂正が完了します。main処理部の最後、
print("* fidelity after error correction:", qs_fin.fidelity(qs_ini))
で、初期状態と誤り訂正後の最終状態との忠実度を表示します。忠実度が1.0となれば誤り訂正は成功です。
結果
実行結果を以下に示します。
* initial state: logical |11>
* add noise
* syndrome measurement: [0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
* error chain: [{'type': 'X', 'qid': [7]}]
* fidelity after error correction: 1.0
シンドローム測定によって1番目と4番目の面演算子が反応して、7番目のビットにビット反転エラーがあったと特定されました。初期状態との忠実度は1.0となり、正しく復元されることがわかりました。
次に、加えるエラーを以下のようにビット・位相反転エラーとしてみました。
# qs_fin.x(7) # bit flip error at #7
qs_fin.z(7).x(7) # bit and phase flip error at #7
実行結果は、
* initial state: logical |11>
* add noise (phase and bit flip): X_7 Z_7
* syndrome measurement: [0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0]
* error chain: [{'type': 'X', 'qid': [7]}, {'type': 'Z', 'qid': [7]}]
* fidelity after error correction: 1.0
となり、こちらも正しく誤り訂正できることがわかりました。
おわりに
これで表面符号の基本が理解できました。トポロジーを駆使することで強力な符号が構成できるのはとても新鮮で興味深かったです。また、個人的にはあまり馴染みがなかった代数的トポロジーについても、参考文献を通して勉強できました。
今回は専らトーラス状に構成した表面符号について説明しましたが、物理的にトーラスをどう実現するの?とか、たとえ実現できたとしても2つの論理ビットしか表現できない(穴が1個の場合ですが)という問題があります。これを打破すべく、トーラスではない単なる平面(ただし欠陥付き)を使った表面符号も提案されているようなので、次回はそれについて勉強してみたいと思います。
謝辞:本記事をまとめるに際し、株式会社Nextremer様が主催されている勉強会「第四回トポロジカル量子計算とその周辺」に参加し勉強させていただきました。ポイントになる部分をわかりやすく講義していただき理解が進みました。この場をお借りし感謝致します。
以上
-
これ大丈夫でしょうか。トーラス上に面演算子が隙間なく敷き詰められています。すべての面演算子を集めると各辺に対応した$Z$演算子は必ず2回登場するのでその積は恒等演算子$I$となります。同様に頂点演算子もトーラス上に隙間なく敷き詰められています。すべての頂点演算子を集めると各辺に対応した$X$演算子は必ず2回登場するのでその積は恒等演算子$I$となります。 ↩
-
このあたり、参考文献3では、鎖複体(chain complex)を使った代数的トポロジーの言葉で一般的に記述されています。正方格子以外にもいろいろなタイプの格子の上で表面符号が考えられそうで面白いのですが、長くなるので本記事では省略します。 ↩
-
連続変形によって一点に収縮させることができるループのことを「自明なループ」と言います。 ↩
-
図では$l_1$を直線で表しましたが、直線ではないループであったとしても頂点演算子と重なる辺は必ず2個になります。図を書いて1分ほど考えればわかると思います。 ↩
-
ここでは、$l_1$を使って1番目の論理ビットに対する$Z$演算子を定義しましたが、縦方向にぐるっと回る非自明なループ(直線でなくても良い)であれば何を使っても良いです。 ↩
-
縦方向にぐるっと回る非自明ループを使うと$\tilde{Z}_1$と同じ効果を表す論理演算になってしまうので、トポロジー的に違うループを使う必要があります。 ↩
-
ちなみに、穴が1個のドーナツ(トーラス)を考えることで2つの論理ビットを表現することができましたが、実は、穴が2個のドーナツを考えると4つの論理ビットを表現することができます。一般に種数$g$の閉曲面を使って$2g$個の論理ビットを表現することができます。種数$g$の閉曲面上に描かれた格子の面、辺、点の数を各々$|F|,|E|,|V|$とすると$|F|+|V|-|E|=2-2g$という関係が成り立つことから証明できます。 ↩
-
$\bar{r}+\bar{c}$が自明なループになるので$X(\bar{r}+\bar{c})$は符号状態に対して何の影響も及ぼしません、という理解でも良いです。 ↩
-
式(17)は一見すると難しそうな感じがするかもしれませんが、$\bar{c}$に含まれる辺の数を$M$としてみると、$p(\bar{c})=(1-p)^{|E|-M} p^{M}=(1-p)^{|E|}(\frac{p}{1-p})^{M}$とできることからわかると思います。 ↩
-
エラー確率を横軸、訂正失敗率を縦軸にとった曲線で誤り訂正符号の特性を表現できますが、それはエラー確率の閾値を変曲点としたS字カーブになります。で、$N$の値を大きくするに従ってS字のカーブがきつくなり、$N$無限大の極限では階段状の特性曲線になります。 ↩
-
これは結構甘い見積もりらしく、実際には$10^{-5}-10^{-6}$と言われているらしいです。 ↩