Advent Calendar 21日目の記事 組合せ最適化でひとりにしてくれを解く
Advent Calendar 23日目の記事 組合せ最適化で波及効果を解く
これなに
不等式を、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
- 各白マスには1からnまでの数字が1つだけ入ります
- 各横行および各縦列には同じ数字が入りません
- 連続する2つのマス目の間に不等号がある場合,それらのマス目に入る数字は不等号の示す大小関係を満たさなければいけません
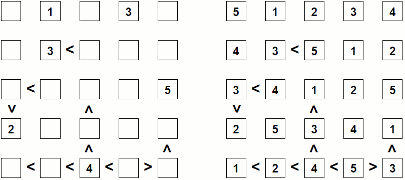
下記は、左が問題で、右が答えです。この問題の解は複数あります。
入力パラメータ
dataにヒントが入っているとします。
python
import numpy as np
from pulp import LpProblem, lpSum, lpDot, value
from ortoolpy import addvars, addbinvars
data = """\
. 1 . 3 .
. 3<. . .
.<. . . 5
V A
2 . . . .
A A
.<.<4<.>.""".splitlines()
n = (len(data)+1)//2
Pythonで解く
数理モデルを作成し、解きましょう。
変数
- v:各位置がどの数字か (1)
- r:各位置の数字 (2)
制約
- $v_{ij}$は1つの数字のみ (3)
- rをvで表現 (4)
- 縦または横に同じ数字が入りません (5)
- 数字が指定されていれば、その数字になること (6)
- 不等号があれば、その関係を満たすこと (7)
python
m = LpProblem()
v = np.array(addbinvars(n, n, n)) # (1)
r = np.array(addvars(n, n)) # (2)
for i in range(n):
for j in range(n):
m += lpSum(v[i,j]) == 1 # (3)
m += lpDot(range(n), v[i,j]) + 1 == r[i,j] # (4)
m += lpSum(v[i,:,j]) == 1 # (5)
m += lpSum(v[:,i,j]) == 1 # (5)
c = data[i*2][j*2]
if c.isdigit():
m += v[i,j,int(c)-1] == 1 # (6)
for i in range(n - 1):
for j in range(n):
c = data[i*2+1][j*2]
if c == 'A':
m += r[i,j] <= r[i+1,j] - 1 # (7)
elif c == 'V':
m += r[i,j] >= r[i+1,j] + 1 # (7)
for i in range(n):
for j in range(n - 1):
c = data[i*2][j*2+1]
if c == '<':
m += r[i,j] <= r[i,j+1] - 1 # (7)
elif c == '>':
m += r[i,j] >= r[i,j+1] + 1 # (7)
m.solve()
結果の表示
python
print(np.vectorize(value)(r).astype(int))
>>>
[[5 1 2 3 4]
[4 3 5 1 2]
[3 4 1 2 5]
[2 5 3 4 1]
[1 2 4 5 3]]
解けていることが確認できます。
以上