Advent Calendar 24日目の記事 組合せ最適化でへやわけを解く
これなに
オーノーを、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
- マスに赤●か青●を必ずいれます
- *は赤●の指定を表します
- 数字は、自身も青●扱いとし、自信を除く上下左右に連なる青●の数を表します
- 単独の青●は禁止します
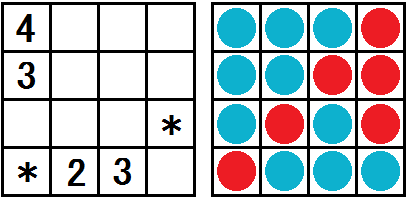
下記は、左が問題で、右が答えです。
入力パラメータ
dataにヒントが入っているとします。
python
import numpy as np
from itertools import product
from pulp import LpProblem, lpSum, value
from ortoolpy import addvars, addbinvars
data = """\
4...
3...
...*
*23.""".splitlines()
n = len(data)
Pythonで解く
数理モデルを作成し、解きましょう。
定式化
\begin{array}{cl}
変数 & x_{ij} \in \{0, 1\} ~ \forall i, j ~ ~ ~ マスi,jが青●か (1) \\
変数 & y_{ijk} \ge 0 ~ \forall i, j, k ~ ~ ~ マスi,jの方向kの青●連続数 (2) \\
\mbox{subject to} & yをxで表す (3) \\
& 数字や*の指定 (4) \\
& 単独青●の禁止 (5) \\
\end{array}
python
def cons(m,x,y,i,j,k,dx,dy,bdi,bdj):
if i == bdi or j == bdj:
m += y[i,j,k] == 0 # (3)
else:
m += y[i,j,k] <= y[i+dx,j+dy,k]+1 # (3)
m += y[i,j,k] <= x[i+dx,j+dy]*(n-1) # (3)
m += y[i,j,k] >= y[i+dx,j+dy,k]+1 - n*(1-x[i+dx,j+dy]) # (3)
m = LpProblem()
x = np.array(addbinvars(n, n)) # 青●か (1)
y = np.array(addvars(n, n, 4)) # 縦、横、上右下左の連続数 (2)
m += lpSum(x) # (3)
for i, j in product(range(n),range(n)):
cons(m,x,y,i,j,0,-1, 0, 0,-1)
cons(m,x,y,i,j,1, 0, 1, -1,n-1)
cons(m,x,y,i,j,2, 1, 0,n-1,-1)
cons(m,x,y,i,j,3, 0,-1, -1,0)
if data[i][j] == '*':
m += x[i,j] == 0 # (4)
elif data[i][j].isdigit():
m += x[i,j] == 1 # (4)
m += lpSum(y[i,j]) == int(data[i][j]) # (4)
else:
m += lpSum(y[i,j]) >= x[i,j]
m.solve()
結果の表示
python
print(np.vectorize(value)(x).astype(int))
>>>
[[1 1 1 0]
[1 1 0 0]
[1 0 1 0]
[0 1 1 1]]
解けていることが確認できます。
まとめ
パズルというテーマでの組合せ最適化は、いかがだったでしょうか?
「面白そう!やってみよう!」と感じていただければ幸いです。
以上