組合せ最適化で凸多角形の最適三角形分割

これなに

数学とコンピュータ・アドベントカレンダーの11日目の記事「凸多角形の最適三角形分割」を組合せ最適化で解いてみました。

考え方

凸N角形に交差しないように、N-3本の対角線を引けば、三角形分割できるので、和が最小のものを選べば良いです。

数理最適化の手順については、数独を通して組合せ最適化を学ぼうをご覧ください。

例題

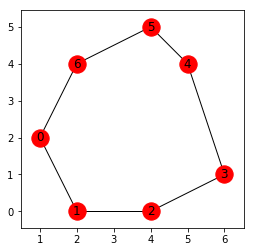
適当に多角形を作ります。

python3

import matplotlib.pyplot as plt
import numpy as np, pandas as pd, networkx as nx
from pulp import LpProblem, lpDot, lpSum, value
from ortoolpy import addbinvars
plt.rcParams['figure.figsize'] = (4,4)
plt.axes().set_aspect('equal', 'datalim')

pos = np.array([[1,2],[2,0],[4,0],[6,1],[5,4],[4,5],[2,4]])
dcpos = dict(enumerate(pos))
n = len(pos)
g = nx.Graph()
g.add_edges_from([(i,(i+1)%n) for i in range(n)])
nx.draw_networkx(g,pos=dcpos)
plt.show()

変数表

変数表を作ります。

python3

a = pd.DataFrame([(i,j,np.linalg.norm(pos[i]-pos[j]))
    for i in range(n) for j in range(i+2,n-(i==0))], columns='I J Dist'.split())
a['Var'] = addbinvars(len(a))
a[:2]

|I|J|Dist|Var
:--|:--|:--|:--|:--
0|0|2|3.605551|v000001
1|0|3|5.099020|v000002

定式化して解く

制約条件は、N-3本必要というのと、交差させないになります。

python3

m = LpProblem()
m += lpDot(a.Dist, a.Var)
m += lpSum(a.Var) == n-3 # N-3本必要
for idx,(i1,j1,_,v1) in a.iterrows():
    for _,(i2,j2,_,v2)  in a[idx+1:].iterrows():
        if i1 < i2 < j1 < j2:
            m += v1+v2 <= 1 # 交差させない
m.solve()
a['Val'] = a.Var.apply(value)
print('対角線の和',value(m.objective))
g.add_edges_from(a[a.Val>0.5].values[:,:2])
nx.draw_networkx(g,pos=dcpos)
plt.show()
>>>
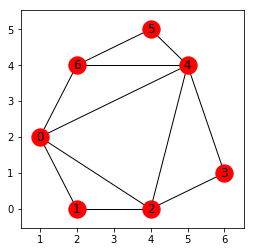
対角線の和 15.200792856081229

できました。

以上