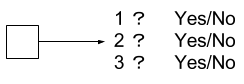初歩からの数理モデル

Pythonの最適化のライブラリである PuLP を用いた数理モデルの作り方を説明します。

数理モデルとは「変数、目的関数、制約条件を数式で表したモデル」です。
詳しくは、下記でご確認ください。

• 組合せ最適化を使おう

前提

• Pythonの文法の基礎的な使い方を知っている（以降ではPython3.6を用いて説明します）。
• 数理最適化について、簡単に知っている。
• ソルバーについて、簡単に知っている。

目標：魔方陣の数理モデルを理解する

下記の「魔方陣の数理モデル」の理解の助けとなるように、基本的なところを説明します。

• 魔方陣を通して組合せ最適化を学ぶ

早速ですが、以降では目的関数は、使わないので無視します（変数と制約条件だけ考えます）。

1x1マスに1から3の数字を入れよう

1x1マスに、1から3の数字をいずれか１つを入れることを考えます。
制約条件として、「1マスの数字の合計が2である」ことを入れましょう。
答えは、2になりますが、その数理モデルをPythonで作成してみましょう。

1つのマスに入る数字（1,2,3）を1つの変数とすると、（魔方陣などの）制約条件を書くのが難しくなります。
そこで、「1かどうか」「2かどうか」「3かどうか」という「YesまたはNo」の値を持つ3つの変数を用意します。

この変数は、「Yesのときに1、Noのときに0の値になる」と定義します。このような、0または1をとる変数を0-1変数またはバイナリー変数とよびます。

3つの変数を、Var1,Var2,Var3としましょう（Varは、変数を意味するvariableの先頭3文字）。

PuLPで数理モデルを作り、解いて、結果をみましょう。
PuLPは、pip install pulpでインストールできます。

first_pulp.py

import pulp

# 数理モデル作成
model = pulp.LpProblem()

# 各変数を作成.cat=pulp.LpBinaryでバイナリ変数として作成
Var1 = pulp.LpVariable('Var1', cat=pulp.LpBinary)
Var2 = pulp.LpVariable('Var2', cat=pulp.LpBinary)
Var3 = pulp.LpVariable('Var3', cat=pulp.LpBinary)

# 1*Var1 + 2*Var2 + 3*Var3 == 2 と言う制約条件をモデルに追加
model += (1*Var1 + 2*Var2 + 3*Var3 == 2)

# Var1 + Var2 + Var3 == 1 と言う制約条件をモデルに追加
condition = (Var1 + Var2 + Var3 == 1)
model += condition

# 数理モデルを解く
model.solve()

# pulp.valueで、最適化された変数を参照
print('Var1', pulp.value(Var1))
print('Var2', pulp.value(Var2))
print('Var3', pulp.value(Var3))
print('Number', pulp.value(1*Var1 + 2*Var2 + 3*Var3))

実行結果

$ python first_pulp.py
Var1 0.0
Var2 1.0
Var3 0.0
Number 2.0

順番に説明します。

• pulp.LpProblem()で数理モデルを作成します。
• pulp.LpVariable('Var1', cat=pulp.LpBinary)で変数Var1を作成します。カテゴリー（cat）に pulp.LpBinary を指定すると、バイナリー変数になります。
• マスの数字は、1*Var1 + 2*Var2 + 3*Var3という式で計算できます。
• 「式 == 数字」は制約条件になります。PuLPでは、式や制約条件が、数式のように書くことができます。
• 制約条件を数理モデルに追加するには、model += conditionのように書きます。
• 1つのマスには、数字は1つしか入れることはできません。これを制約条件で書くと、Var1 + Var2 + Var3 == 1となります。
• model.solve()は、簡単なコマンドですが、下記の一連の処理を実行し、数理モデルを解いて、結果を得ることができます。
  • 数理モデルを「ソルバーの必要とする形式」でファイルに出力し、ソルバーの入力とする。
  • ソルバーを実行する。ソルバー内では、シンプレックス法や分子限定法などで解を計算し、結果をファイルに出力する。
  • ソルバーの出力したファイルを読み取り、数理モデルの変数に、結果の値を設定する。
• pulp.value(Var1)のようにして、変数Var1の値を取り出せます。
• pulp.valueは、変数だけでなく式も指定できます。pulp.value(1*Var1 + 2*Var2 + 3*Var3)でマスの数字を取り出せます。

PuLPによる数理モデルの使い方のイメージがつかめたでしょうか。
人が簡単にできることを、数理モデルで計算すると手間がかかりますね。
プログラム（Python）の良いところは、変数の数が増えてもプログラム自体は増えないことです。
すなわち、人間が暗算できないような計算もプログラムならシンプルに記述できます。

リストを使って書き換える

全く同じ問題を、リストを使って書いてみましょう。
リストを使うと、問題のサイズが増えてもプログラムを変えないで済むようになります。

second_pulp.py

import pulp

# 数理モデルを作成
model = pulp.LpProblem()

# 3つの変数をバイナリ変数で作成
Var = [pulp.LpVariable(f'Var{i}', cat=pulp.LpBinary) for i in range(3)]

# マスに入る数字の合計が２である制約条件を追加
model += (pulp.lpDot([1, 2, 3], Var) == 2)

# マスに入る数字が1つである制約条件を追加
model += (pulp.lpSum(Var) == 1)

# 数理モデルを解く
model.solve()

# 結果を参照
for v in Var:
    print(v.name, pulp.value(v))
print('Number', pulp.value(pulp.lpDot([1, 2, 3], Var)))

実行結果

$ python second_pulp.py
Var1 0.0
Var2 1.0
Var3 0.0
Number 2.0

同じ結果になりました。適宜説明します。

• lpDot([1,2,3], Var)は内積の和を計算します。1*Var[0] + 2*Var[1] + 3*Var[2]と同じ意味になります。
• lpSum(Var)はリストVarの和になります。sum(Var)と値は一緒ですが、lpSumを使うようにしましょう。理由は下記をご覧ください。
  • 数理モデルにおける変数の和

pandasを使った数理モデル

ここでは、さらにデータ分析ライブラリ（pandas）を使った数理モデルの作成方法をご紹介します。
pandasには、データを整形するための豊富な機能が用意されており、簡単にデータの整形をすることができます。
つまり、pandasで整形したデータを使ってpulpを実行できると、数理モデルを簡単に記述できるようになります。

third_pulp.py

import pulp
import pandas

# 数理モデルを作成
model = pulp.LpProblem()

# データフレームに変数と定数を追加
df = pandas.DataFrame()
df['Number'] = [1, 2, 3]
df['Var'] = [pulp.LpVariable(f'Var{i}', cat=pulp.LpBinary) for i in range(3)]

# 数理モデルに制約条件を追加
model += (pulp.lpDot(df.Number, df.Var) == 2)
model += (pulp.lpSum(df.Var) == 1)

# 数理モデルを解く
model.solve()

# 結果を表示
df['Value'] = df.Var.apply(pulp.value)
print(df)
print('Number', df[df.Value==1].Number.iloc[0])

実行結果

$ python third_pulp.py
   Number   Var  Value
0       1  Var0    0.0
1       2  Var1    1.0
2       3  Var2    0.0
Number 2

違いを見ていきましょう。

• リストVarがpandas.Seriesのdf.Varに変わりました。Varのように先頭を大文字にすることによって、pandas.DataFrameのメソッドと区別できます（小文字だと、たまたまメソッドと同じ名前をつけて、バグの原因になる可能性があります）。
• df['Value'] = df.Var.apply(pulp.value)が追加されました。これは、Varの結果を表す実数の列（Series）を追加しています。このようにすると、変数に対応する結果が簡単にわかり、扱いやすくなります。この書式はイディオムだと思って覚えましょう。
• 0-1変数を使った数理モデルでは、1になった変数が重要な意味を持ちます。pandasを使うと、df[df.Value==1]のように簡単に取り出すことができます。ここでは、要素数が1なので、df[df.Value==1].Number.iloc[0]でマスに入る数字がわかります。
• 簡単な数理モデルでは pandasの良さがわかりにくいと思いますが、複雑になるとプログラムのわかりやすさが かなり変わってきます。もっと、具体的に見てみたいと思ったら、「数独を通して組合せ最適化を学ぼう」をご覧ください。

補足

df['Var'] = [LpVariable(f'Var{i}', cat=LpBinary) for i in range(3)]は、よく使うフレーズではありますが、記述が大変です。
ortoolpyというライブラリを使うと、下記のように簡潔に記述できます。インストールは、pip install ortoolpyでできます。

python3

from ortoolpy import addbinvars
df['Var'] = addbinvars(len(df))

以上