組合せ最適化でチョコナを解く

Advent Calendar 8日目の記事 組合せ最適化でのりのりを解く
Advent Calendar 10日目の記事 組合せ最適化でクリークを解く

これなに

チョコナを、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。

自分でも試してみたい人は、下記を参考にしてください。

• 数独を通して組合せ最適化を学ぼう

問題

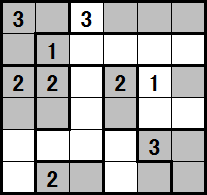
• 国(太線で区切られた部分)の数は、国内の黒マスの合計とする。国の数がない場合はいくつでもよい。
• 黒マスの連なりは、長方形とする。

下図の薄いグレーが解です。

Pythonでは、data（黒マスの数）、area（国のグループ）を使うことにします。

python

import pandas as pd, matplotlib.pyplot as plt
from pulp import LpProblem, lpSum, value
from ortoolpy import addbinvars
data = """\
3.3...
.1....
22.21.
......
....3.
.2....""".splitlines()
area = """\
001111
022222
345677
345677
355899
3aa889""".splitlines()

変数表

下記のような変数表を作成します。各行の変数は0または1をとります。
変数の値が1ならば、該当行 該当列のマスが黒になります。

	行	列	字	国	Var
0	0	0	3	0	v000001
1	0	1	0	0	v000002
...	...	...	...	...	...

python

ni, nj = len(data), len(data[0])
a = pd.DataFrame([(i,j,data[i][j],area[i][j]) for i in range(ni)
    for j in range(nj)], columns=list('行列字国'))
a.字 = a.字.apply(lambda c: int(c) if c.isdigit() else 0)
a['Var'] = addbinvars(len(a))
a[:2]

数理モデルを作り解く

変数表ができたので、チョコナの解になるように、制約条件を追加し数理モデルを作成し、解きましょう。

• 各国の黒の数を指定した数に。
  • 数字は1つだけなので、合計をとれます。注意点として、合計が0なら制約条件にしないことです。
• 黒の形を長方形にする。
  • 任意の2x2の4マスの黒の合計が3にならないということです。
  • 合計を3にしてはいけないという制約条件は、「4マスの黒の合計 <= 2+2*1マスの黒の合計」を4マスの中の各マスで見れば、OKです。
    • 何故なら、3のときだけ、「3<=2」という状態が出て成り立たないためです。

python

m = LpProblem()
for g,v in a.groupby('国'):
    if v.字.sum():
        m += lpSum(v.Var) == v.字.sum()
for i in range(ni-1):
    for j in range(nj-1):
        v = a.query(f'{i}<=行<={i+1}&{j}<=列<={j+1}').Var
        for x in v:
            m += lpSum(v) <= 2+2*x
m.solve()

結果の表示

python

a['Val'] = a.Var.apply(value)
plt.imshow((a.Val<0.5).values.reshape(ni,nj), cmap='gray', interpolation='none')
plt.show()

解けていることが確認できます。

以上