これなに
「たけしの コマ大 数学科」の問題のうち最適化で解けそうなものを試してみました。
Pythonで実行するための準備
python
import scipy.optimize, numpy as np, networkx as nx
from itertools import product
from pulp import *
from ortoolpy import addvar, addvars, addbinvar, addbinvars
先にimportしておきます。
割り当て問題
野球選手Ａ～Ｅをポジションに割り当てて、チームの戦力をベストにする(数値は、低いほどよい)。
| 選手 | 1塁 | 2塁 | 3塁 | SS | 外野 |
|---|---|---|---|---|---|
| A | 6 | 5 | 6 | 5 | 6 |
| B | 8 | 7 | 6 | 8 | 7 |
| C | 4 | 5 | 4 | 4 | 5 |
| D | 6 | 7 | 6 | 4 | 7 |
| D | 10 | 8 | 10 | 7 | 10 |
最小重み完全マッチング問題ですね。
python
w = np.array([[6,5,6,5,6],
[8,7,6,8,7],
[4,5,4,4,5],
[6,7,6,4,7],
[10,8,10,7,10]])
N = len(w)
g = nx.Graph()
for i,j in product(range(N),range(N)):
g.add_edge(i, j+N, weight=w.max()-w[i][j])
r = nx.max_weight_matching(g)
for i in range(N):
print('ABCDE'[i], ['1塁','2塁','3塁','SS','外野',][r[i]-N])
>>>
A 外野
B 3塁
C 1塁
D SS
E 2塁
同じ答えが出ました。
集合場所問題
1~5の人が1か所に集まるのに移動距離の総和が最小になる場所は？
非線形最適化問題になります。
距離をL2ノルムで考えると、ウェーバー問題ですね。
python
pos = np.array([[1,2,1],[3,7,5],[5,3,2],[6,5,2],[7,1,3]]) # x,y,人数
def func(x):
return sum(p[2]*np.linalg.norm(p[:2]-x) for p in pos)
print(scipy.optimize.fmin(func, [0,0]))
>>>
[ 4.80539237 4.38561398]
碁盤目状なので、L1ノルムも計算してみます。
python
m = LpProblem()
vx = addvar(cat=LpInteger)
vy = addvar(cat=LpInteger)
vp = addvars(pos.shape[0])
vq = addvars(pos.shape[0])
m += lpDot(pos[:,2], vp) + lpDot(pos[:,2], vq)
for i in range(pos.shape[0]):
m += vp[i] >= pos[i,0]-vx
m += vp[i] >= -(pos[i,0]-vx)
m += vq[i] >= pos[i,1]-vy
m += vq[i] >= -(pos[i,1]-vy)
m.solve()
print(value(vx),value(vy))
>>>
5.0 5.0
中国人郵便配達問題
郵便局から出発して、すべての家に郵便物を配達し、再び、郵便局に戻る、この間の移動距離が最小となるような経路を見つけよ
全ての辺を周る問題を中国人郵便配達問題といいます。
一筆書き(オイラー閉路)できれば、最小なのは自明です。次数が奇数の点をなくせば一筆書きできるので、奇数次数の点だけで距離を重みにして、最小重み完全マッチング問題を解けばよいです。
オイラー閉路は、nx.eulerian_circuitで求められます。
プログラムは省略します。
靴ひも問題
1列に8個ずつ、計16個の穴があいた靴に、きちんと履けるように靴ひもを通したとき、最短の長さ（結び目までの長さ）を求めよ！ それぞれの穴は、必ず、反対側の列の穴につながっていなければならない。
グラフを作ります。
python
N = 8
g = nx.Graph()
for i in range(N):
g.add_edge(i,i+N)
if i<N-1:
g.add_edge(i,i+N+1)
if i:
g.add_edge(i,i+N-1)
g.add_edge(i-1,i)
g.add_edge(i+N-1,i+N)
nx.draw_networkx(g)
解いてみます。
python
def len_(i,j):
k =abs(i-j)
return 1 if k==1 else 2 if k==N else 2.236
m = LpProblem()
# 変数作成
for i,j in g.edges():
g.edge[i][j]['Var'] = addbinvar()
m += lpSum([len_(i,j)*g.edge[i][j]['Var'] for i,j in g.edges()]) # 目的関数
for i in range(2*N):
# 点には入りと出がある
m += lpSum(dc['Var'] for dc in g.edge[i].values()) == 2
m += lpSum(dc['Var'] for j,dc in g.edge[i].items()
if abs(i-j) >= N-1) >= 1 # 反対側と結ぶ
for k in range(1,N-2):
# 連結させる
m += lpSum(g.edge[i][j]['Var'] for i,j in
[[k,k+1],[k,k+N+1],[k+N,k+1],[k+N,k+N+1]]) == 2
m.solve()
print(value(m.objective))
for i,j in g.edges():
if value(g.edge[i][j]['Var']) > 0:
print((i,j), end=', ')
>>>
25.416000000000004
(0, 8), (0, 1), (8, 9), (9, 2), (1, 10), (10, 11),
(2, 3), (11, 4), (3, 12), (12, 13), (4, 5), (13, 6),
(5, 14), (14, 15), (6, 7), (15, 7),
同じ答えになりました。
カックロ
表裏に0～9までの数字がひとつずつ書かれたカードが5枚ある（数字の重複はない）。すべて表の数を足すと「19」、左から3枚を裏返して、見えている数を合計すると「20」になった。同様に、裏裏表裏裏の場合は「35」、表表裏表裏の場合は「11」、表裏表裏表の場合は「31」になった。最初に見えていたカードの表にあった数を並び順に答えよ！
python
hint = [[(1,1,1,1,1),19],
[(0,0,0,1,1),20],
[(0,0,1,0,0),35],
[(1,1,0,1,0),11],
[(1,0,1,0,1),31]]
r = range(10)
m = LpProblem()
v = addbinvars(10,10) # i:位置,j:数字
for i in r:
m += lpSum(v[i]) == 1
m += lpSum(v[j][i] for j in r) == 1
for ptn,n in hint:
m += lpSum(lpDot(r,v[i if j else i+5])
for i,j in enumerate(ptn)) == n
m.solve()
print((np.vectorize(value)(v)@r).reshape(2,-1))
>>>
[[ 3. 1. 9. 2. 4.]
[ 6. 8. 0. 7. 5.]]
同じ答えです。
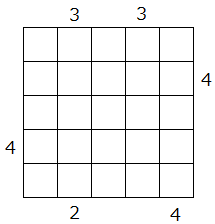
ビル
ビルディングパズルですね。
python
n = 5
hint = [([0,3,0,3,0], 1, 0, 0, 0, 0, 1),
([0,2,0,0,4], 1, 0, 0, n-1, 0, -1),
([0,0,0,4,0], 0, 1, 0, 0, 1, 0),
([0,4,0,0,0], 0, 1, n-1, 0, -1, 0)]
m = LpProblem()
v = np.array(addbinvars(n, n, n))
r = np.array(addvars(n, n))
def add(m, r, k, p, q, y, x):
if k==0:
return
u = addbinvars(n-1)
m += lpSum(u) == k - 1
vmx = r[p,q]
for i in range(1,n):
vnx = r[p + y*i][q + x*i]
m += vmx + n * u[i-1] >= vnx + 1
m += vmx + 1 <= vnx + n - n * u[i-1]
vtm = addvar()
m += vmx <= vtm
m += vnx <= vtm
vmx = vtm
m += vmx <= n
for i in range(n):
for j in range(n):
m += lpSum(v[i,j,:]) == 1
m += lpDot(range(n), v[i,j]) + 1 == r[i,j]
m += lpSum(v[i,:,j]) == 1
m += lpSum(v[:,i,j]) == 1
for h in hint:
add(m, r, h[0][i], h[1]*i+h[3], h[2]*i+h[4], h[5], h[6])
m.solve()
np.vectorize(value)(r).astype(int).T.tolist()
>>>
[[4, 1, 3, 2, 5],
[5, 4, 1, 3, 2],
[3, 5, 2, 1, 4],
[1, 2, 4, 5, 3],
[2, 3, 5, 4, 1]]
こちらも同じ答えです。
以上