やったこと
- Scikit learnのチュートリアルを参考に
- ラベル付のデータセットを使って
- kの値や重みを変えて
- pythonでk近傍法を実装
サンプルデータのimport
irisデータセットを使う。入力データは4次元だけど、可視化しやすいように最初の2次元だけを使う。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets, metrics
iris = datasets.load_iris() # 4次元、150サンプルのデータセットで
# 植物の萼(がく)の長さ、幅、 花びらの長さ、幅、単位はcm。
iris_X = iris.data[:, :2] # 4次元のうち、最初の2次元の特徴量だけを使用
iris_y = iris.target # 正解ラベル, 0, 1, 2の3種類
教師データとテストデータに分割
np.random.seed(0) # 乱数のシード設定、0じゃなくてもなんでもいい
indices = np.random.permutation(len(iris_X)) # 0~149の数字をランダムに並び替え
# 140個のデータセットを105個の教師データと35個のテストデータに分ける
iris_X_train = iris_X[indices[:-35]]
iris_y_train = iris_y[indices[:-35]]
iris_X_test = iris_X[indices[-35:]]
iris_y_test = iris_y[indices[-35:]]
カラーマップの作成
正解ラベルの個数に応じて3色作成。2つあるのは、教師データ用(cmap_bold)と学習結果用(cmap_light)。
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
変数の設定
今回使用する識別器はKNeighborsClassifier。変数のkが最も重要で、サンプルデータに最も近いk個のデータがどのラベルに属するかを調べ、その多数決でサンプルデータのラベルを分類する。デフォルトは5。
今回取り上げるもうひとつの変数である"weights"には、"uniform"と"distance"の2つが用意されている。
- uniform:データ間の距離によらず一様な重みを与える。デフォルトはこれ。
- distance:距離が近いデータほどその影響が大きくなるよう、距離に反比例して重みが与えられる。
他にも algorithm などの変数がある。詳しくはこちら。
h = 0.1 # メッシュサイズ
k_list = [1, 5, 10, 30] # k の数
weights_list =['uniform', 'distance']
score = np.zeros((len(k_list)*2,5)) # score
学習と結果の可視化
入力が2次元データなので、カラーマップで分類境界を表示してみる。
plt.figure(figsize=(8*len(k_list), 12))
i = 1 # subplot用
for weights in weights_list:
for k in k_list:
clf = neighbors.KNeighborsClassifier(k, weights=weights)
clf.fit(iris_X_train, iris_y_train)
x1_min, x1_max = iris_X[:, 0].min() - 1, iris_X[:, 0].max() + 1 # Xの1次元目の最小と最大を取得
x2_min, x2_max = iris_X[:, 1].min() - 1, iris_X[:, 1].max() + 1 # Xの2次元目の最小と最大を取得
# x1_min から x1_max まで、x2_min から x2_max までの h 刻みの等間隔な格子状配列を生成
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, h), np.arange(x2_min, x2_max, h))
# メッシュ状の各点に対して予測 / .ravel()で一次元配列に変換し、np.c_[]でxx1, xx2をxx2ごとに合体
Z = clf.predict(np.c_[xx1.ravel(), xx2.ravel()])
Z = Z.reshape(xx1.shape) # 配列形式変更
plt.subplot(2,len(k_list),i) # 2行 × k_list列のグラフのi番目のグラフに
plt.pcolormesh(xx1, xx2, Z, cmap=cmap_light) # 学習結果をプロット
plt.scatter(iris_X_train[:, 0], iris_X_train[:, 1], c=iris_y_train, cmap=cmap_bold) # 教師データをプロット
plt.scatter(iris_X_test[:, 0], iris_X_test[:, 1], c=iris_y_test, cmap=cmap_light) # テストデータをプロット
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.title("k = %i, weights = '%s'" % (k, weights), fontsize=30)
score[i-1,3] = k
score[i-1,0] = metrics.f1_score(iris_y_test, clf.predict(iris_X_test),average='weighted')
score[i-1,1] = metrics.precision_score(iris_y_test, clf.predict(iris_X_test))
score[i-1,2] = metrics.recall_score(iris_y_test,clf.predict(iris_X_test))
i = i + 1
plt.show
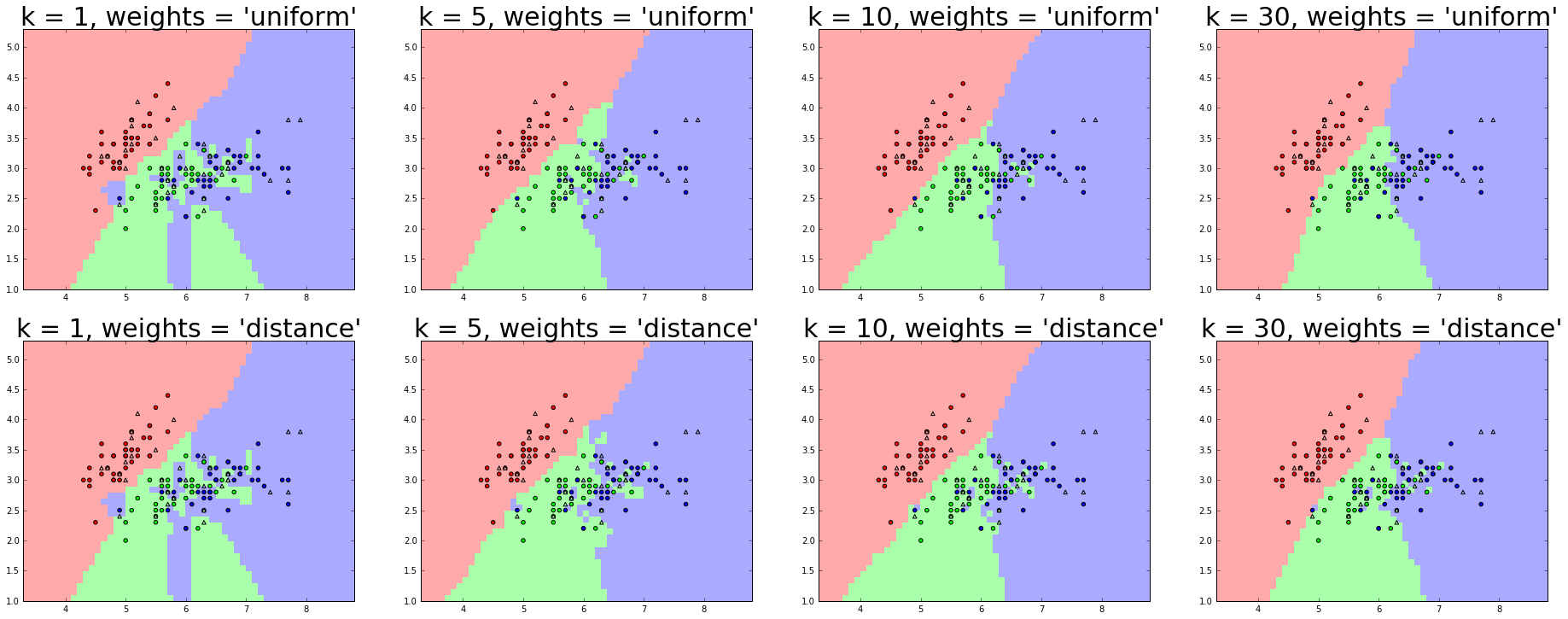
結果はこんな感じ。グラフ上段がuniformの場合、下段がdistanceの場合。
左に行くほどkが大きくなる。可視化できるって素晴らしい。
- kが小さいと過学習気味
- distance のほうが境界線がもっともらしいように見える
- だけど、f値を見ると、uniformの方が良い
- k = 1 のときは当然ながらどちらの重みを使っても結果は同じ
グラフ作成の練習用に、テストデータのf値をプロットしてみる。
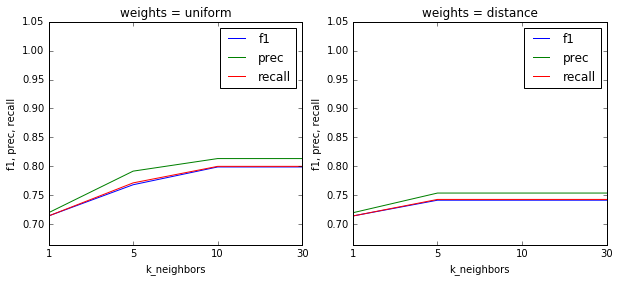
plt.figure(figsize=(10, 4))
i = 0
for weights in weights_list:
plt.subplot(1,2,i+1)
plt.plot(score[i*len(k_list):(i+1)*len(k_list),0])
plt.plot(score[i*len(k_list):(i+1)*len(k_list),1])
plt.plot(score[i*len(k_list):(i+1)*len(k_list),2])
plt.xticks([0,1,2,3],k_list)
plt.ylim(score[:,:3].min()-0.05, 1.05)
plt.title("weights = %s" % weights)
plt.legend(('f1', 'prec', 'recall'), loc='upper right')
plt.xlabel("k_neighbors")
plt.ylabel("f1, prec, recall")
i = i + 1
plt.show
今回は、可視化のために特徴量を2つに減らしてでやったけれど、特徴量を増やすと過学習を抑えつつ精度を高めることができるか確かめてみたい。