今回は分子群に対してそれぞれMorganフィンガープリントを作成し、
それを用いてタニモト係数を計算することで分子の類似性を評価する手順を紹介します。
これまでの記事のシリーズは以下を御覧ください。
[RDKit入門①:まずは環境構築][1]
[RDKit入門②:1分子の読み込みと部分構造検索][2]
[RDKit入門③:複数分子の読み込み (前編)と分子群の描画][3]
[RDKit入門④:複数分子の読み込み (後編)とデータフレームの加工][4]
[RDKit入門⑤:データフレーム内の分子群に対する部分構造検索][5]
[1]:https://qiita.com/Ru-PNP/items/ed5a8530611ef0d712b7
[2]:https://qiita.com/Ru-PNP/items/58d733ef327677d273fd
[3]:https://qiita.com/Ru-PNP/items/1cea34b864e993e4e1e1
[4]:https://qiita.com/Ru-PNP/items/62a108d92c1ddd522e58
[5]:https://qiita.com/Ru-PNP/items/b469ac1b907909a9d821
環境
- Windows 10
- python 3.8.8
- RDKit 2021.03.1
先にパッケージの読み込みを行います。
import pandas as pd
from rdkit import Chem
from rdkit.Chem import AllChem, DataStructs, Draw
import numpy as np
import time
from itertools import chain
# パッケージの読み込み
今回もPlatinum Dataset 2017由来の分子群を用いて作業を行います。
データの入手と加工に関しては以下の記事を御覧ください。
[RDKit入門④:複数分子の読み込み (後編)とデータフレームの加工][4]
この記事で作成したpickleファイルを読み込むところから作業を再開します。
df_Pt = pd.read_pickle("platinum_dataset_2017.pkl")
# platinum_dataset_2017.pklを読み込み、得られたデータフレームをdf_Ptと定義した。
Morganフィンガープリントの作成
まずは1分子に対してMorganフィンガープリントを作成してみましょう。
isoquinoline = Chem.MolFromSmiles("c1nccc2c1cccc2")
# イソキノリンを定義した。
isoquinoline_MF = AllChem.GetMorganFingerprintAsBitVect(isoquinoline, 2, 2048)
# イソキノリンのMorgan Fingerprint(半径2, 2048ビット)を計算し、isoquinoline_MFと定義した。
AllChem.GetMorganFingerpprintAsBitVect関数を用いる場合、引数として
- molオブジェクト
- 探索距離(半径, 2~3が多い?)
- ビット長(短すぎると衝突が問題になるため1024以上を指定するのが一般的?)
の3つを指定します。
同じようにdf_Ptに格納されている分子群についてもMorganフィンガープリントを計算してみます。
df_Pt['Morgan_fp'] = df_Pt['ROMol'].map(lambda x: AllChem.GetMorganFingerprintAsBitVect(x, 2, 2048))
# Morgan Fingerprint(半径2, 2048ビット)を計算し、Morgan_fpの列に格納した。
タニモト係数の計算
一分子ごとにタニモト係数を計算したい場合はDataStructs.TanimotoSimilarity関数を使用します。
試しにdf_Ptの0番目と1番目に格納されている分子のタニモト係数を計算してみます。
引数としては2分子のフィンガープリントを指定します。
Tanimoto_0_1 = DataStructs.TanimotoSimilarity(df_Pt['Morgan_fp'][0], df_Pt['Morgan_fp'][1])
# df_Ptの0番目の分子と1番目の分子のタニモト係数を計算し、Tanimoto_0_1とした。
print(Tanimoto_0_1)
# 0.11578947368421053
ある一分子に対して複数分子のタニモト係数を一挙に計算したい場合もあると思いますが、
その場合はDataStructs.BulkTanimotoSimilarity関数を使用します。
試しにイソキノリンに対するdf_Pt中の分子群のタニモト係数を計算してみましょう。
df_Pt['Tanimoto'] = DataStructs.BulkTanimotoSimilarity(isoquinoline_MF, df_Pt['Morgan_fp'])
# df_Pt中の分子に対し、イソキノリンに対するタニモト係数を計算してTanimotoの列に格納した。
引数としては
- 基準となる分子のフィンガープリント
- 分子群のフィンガープリントのリスト
の2つを指定します。
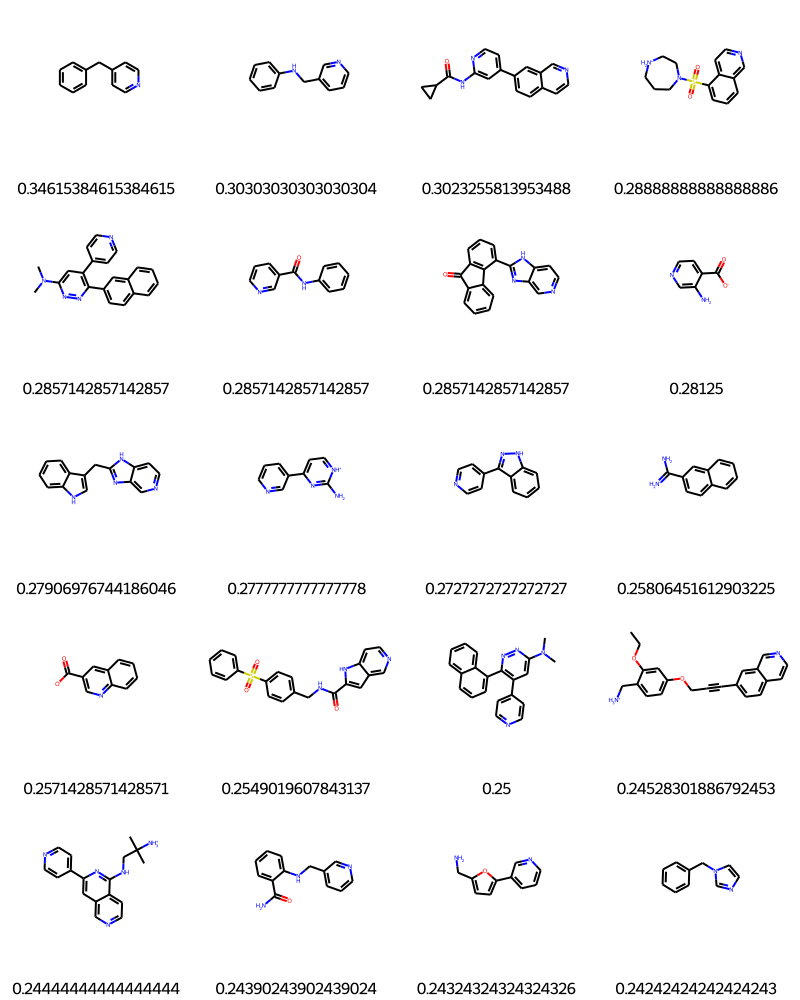
以上の操作でイソキノリンに対するタニモト係数が計算できました。
せっかくなので、Morganフィンガープリントを基準に考えたときどんな分子が
イソキノリンと似ているとされるのか確認してみましょう。
df_Pt_sort = df_Pt.sort_values(by = 'Tanimoto', ascending = False)
df_Pt_sort = df_Pt_sort.reset_index(drop = True)
# タニモト係数が大きい順にソートし、df_Pt_sortと定義し、さらにインデックスを振り直した。
Draw.MolsToGridImage(df_Pt_sort['ROMol'], molsPerRow = 4, legends = [str(x) for x in df_Pt_sort['Tanimoto']], maxMols = 20)
# df_Pt_sortの最初の20個の分子を描画した。
Morganフィンガープリントを用いてタニモト係数を計算するとこのような結果となりました。
フィンガープリントの作成方法や分子類似性評価の方法には様々な手法がありますので、
記事末尾のリンクも参考にしていただけると幸いです。
Platinum Dataset 2017には4,548個の分子が格納されています。
これらに対して互いにタニモト係数を計算させてみましょう。
まずは愚直に4,548 × 4,548 = 20,684,304回の計算を行う方法を試してみます。
ついでに計算時間についても測定してみます。
t1 = time.time()
sim_matrix = [DataStructs.BulkTanimotoSimilarity(x, df_Pt['Morgan_fp']) for x in df_Pt['Morgan_fp']]
sim_array = np.array(sim_matrix)
t2 = time.time()
# 4548個の分子について互いにタニモト係数を計算した行列をつくり、sim_matrixと定義した。
# sim_matrixをnumpyのarrayに変換し、sim_arrayと定義した。
print(t2 - t1)
# 67.75742793083191
使用するPCのスペックに依存しますが、約1分程度の時間がかかりました。
しかし、以下を考えると上記の約2千万回の計算には半分ほど無駄な計算が含まれています。
- 互いに同じ分子のタニモト係数は1になる
- m番目の分子に対するn番目の分子のタニモト係数と、n番目に対するm番目の係数は同一
以上をふまえると、n個の分子に対してn^2回の計算を行う必要はなく、
n(n - 1)/2回の計算を行えば知りたい情報を得ることができます。
以下、不要な部分を省いて計算し、三角行列を作成してみます。
t3 = time.time()
sim_array_tri = np.zeros((len(df_Pt), len(df_Pt)))
for i in range(1, len(df_Pt['ROMol'])):
sim_array_tri[i, :i] = DataStructs.BulkTanimotoSimilarity(df_Pt['Morgan_fp'][i], df_Pt['Morgan_fp'][:i])
t4 = time.time()
# df_Ptに格納されている分子数をnとしたとき、n×nの零行列を用意しsim_array_triと定義した。
# 互いにタニモト係数を計算し(重複、自分自身の計算なし)、sim_array_triに格納した。
print(t4 - t3)
# 34.53007674217224
n×nの零行列を用意し、そこへi番目の分子に対するi - 1番目までの分子のタニモト係数を格納し、
下三角行列を作成することで計算量を減らしてみました。
実際、計算に要する時間は約半分になりました。
(もっとうまい方法がありましたらコメントいただけると幸いです)
先に「互いに同じ分子のタニモト係数は1になる」と述べました。
では「タニモト係数が1となる2つの分子は同一分子か?」というと、必ずしもそうとは限りません。
試しにタニモト係数が1となる組み合わせを見てみましょう。
indices = np.where(sim_array_tri == 1)
indices_pair = [(i, j) for i,j in zip(*indices)]
# sim_array_triの中のタニモト係数が1である座標を求め、indices_pairに格納した。
len(indices_pair)
# 27
27の分子ペアはタニモト係数が1であるということが分かりました。
では、どんな分子同士のタニモト係数が1となったか見てみましょう。
pairs_list = []
for i, j in indices_pair:
pairs = [df_Pt['ROMol'][i], df_Pt['ROMol'][j]]
pairs_list.append(pairs)
# タニモト係数が1となる分子のペアをpairs_listに格納した。
pairs_unite = list(chain.from_iterable(pairs_list))
Draw.MolsToGridImage(pairs_unite, molsPerRow = 2, maxMols = len(pairs_unite))
# タニモト係数が1となる分子のペアを描画した。
アルキル基の長さ違いや二糖・三糖等でタニモト係数が1と計算されているようです。
Morganフィンガープリントを作成する際の半径・ビット長を考えると納得の結果です。
おわりに
今回はRDKitを用いて以下の内容を実施いたしました。
- Morganフィンガープリントの作成
- フィンガープリントを用いたタニモト係数の計算
今回紹介した手法にはまだ改善の余地が残されていると思うので、
より計算負荷の少ない方法がありましたらコメントいただけると幸いです。