最小二乗法や最急降下法は知っている前提
知らなければ昔記事にしたので良ければそちらへ
「最小二乗法・最急降下法」を動く図で理解する
最初から幾何の空間で考えられていたらこの記事は必要ない
線形回帰のイメージ
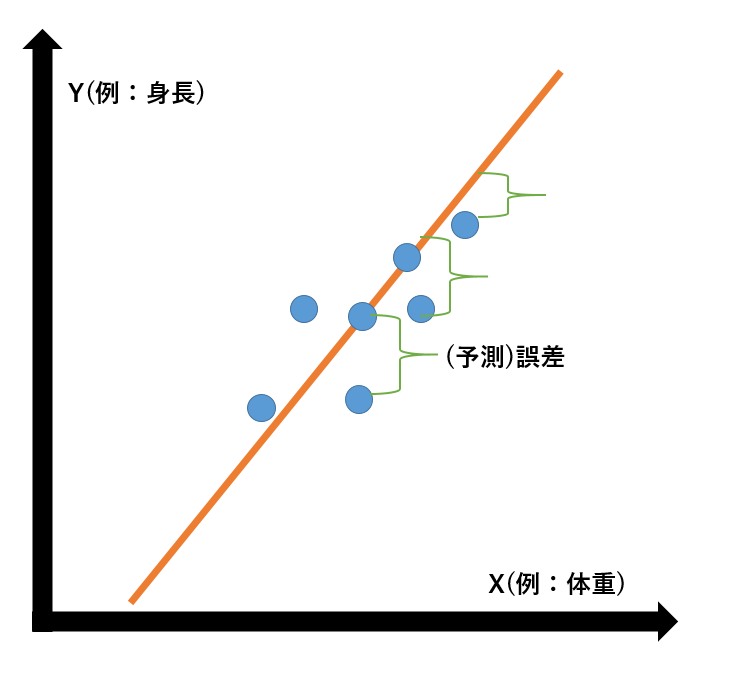
私は最初こんなイメージでした
・実測値のド真ん中(平均)を通る
・傾きβの直線を引いた時、実測値からの距離(予測誤差)の合計が最も小さい
そんな**"傾き"**を求めるものである
と思ってました(別に解釈の一つとして間違ってはいない。。と思う)
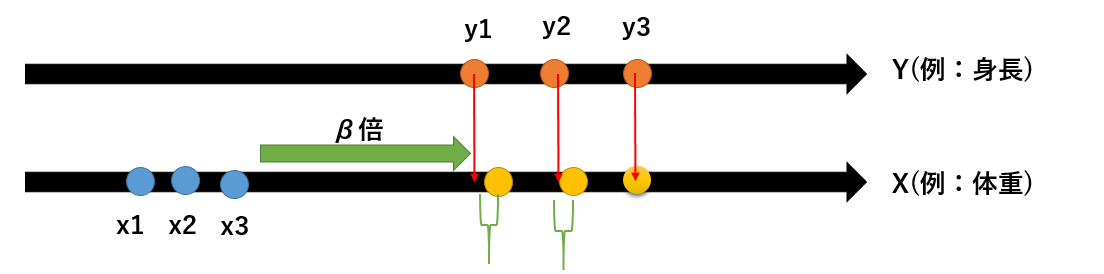
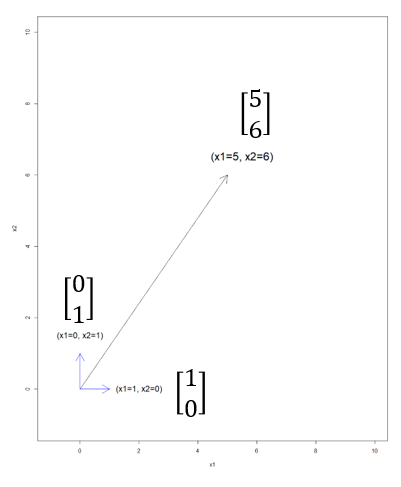
Xという一次元上で考えてみると?
Y=βXとは、すなわち定数倍したXである
図のように平行で走る軸上がYであった時、Xを何倍にしたら尤もらしい値になるか
というのが回帰係数の役割である
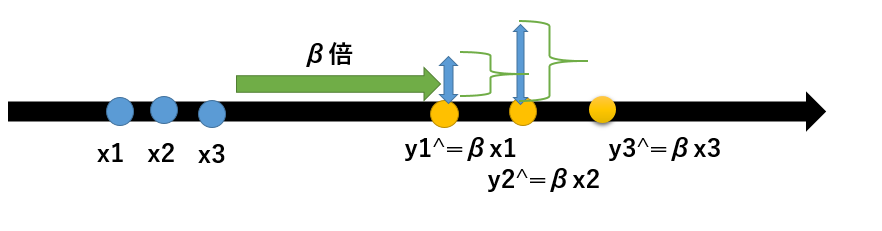
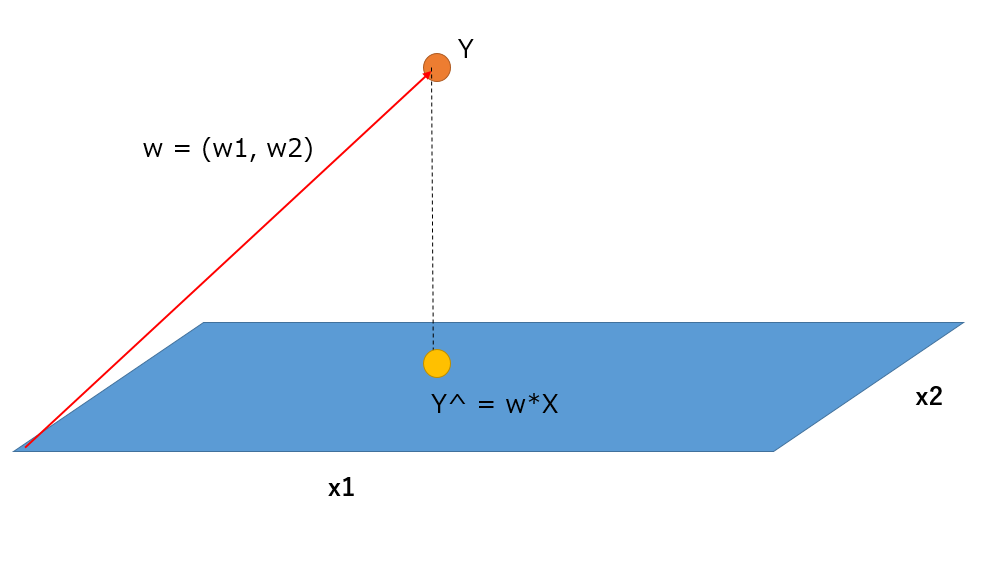
実測値と予測値の誤差はどうしても出てくる
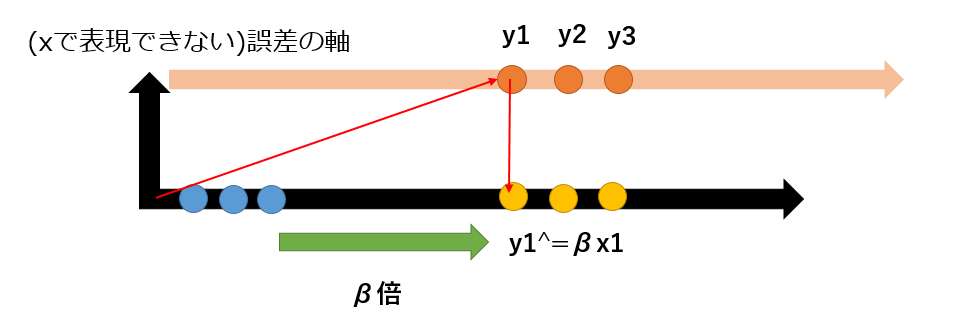
これはXに直交する軸の値であると考える(表現できない値は直行する軸に押し付ける)
この誤差を最も最小にするのは、平行するYから垂直に下してきた時である
(三平方の定理的に)
垂直に下すことを実現させるβを見つけるために最小二乗法が実行される
つまり、係数βは、Xで張る空間(Xの定数倍や線形和)へ実測値Yを垂直に正射影するためのベクトル
係数βは誤差を表現することはできないので、最終的にはXの張る平面空間上のベクトルである
以上
という事を最近知ったので、なるべく図として表現しとく。
これを考えるとカーネル法の入門が楽になるので、次回続きで書く。