今更感がすごいが・・・
理論を本で勉強したら、自分でゴリゴリ実装すると理解が早いってAndrew先生も言ってますし、
今日は最急降下法をRで実装します。
特に数学に強いわけでもない私が、同じ気持ちの方に発信するものなので、
ハイレベルな方はその点をご了承ください。
修正依頼・アドバイス大歓迎です。
こんな問題があるとする
例えば体重から身長を推定したいという依頼があったとする。
(技術書には想像しやすいように、身長・体重という例が出てくるが、広告クリック数と購入者数とか、自分の適応したい問題に置き換えても問題ない)
このような推定を行うとき、
推定したい対象を「目的変数」:身長
推定するために使用するデータを「説明変数」:体重
と言う。
つまり目的変数は一次式(変数が一つの式)のyに相当し、
説明変数は一次式の変数そのもの。つまりxに相当する。
y=ax+b
(身長) = a × (体重) + b
この時、aやbという係数や切片と呼ばれる者たちを、"パラメータ"と呼ぶ。
少し話を逸れて:多項式の時の話
多変数から目的変数を予測するときを考える。
例えば、「身長」を、「体重」と「腕の長さ」・「足の長さ」という三変数から推定するとしよう。
式は
(身長) = a1 × (体重) + a2 × (腕) + a3 × (足) + b
になる。
数式で表すと
y = a_1x_1 + a_2x_2 + a_3x_3 + b
となる。
bの切片項だが、この項は「変数xにパラメータaがかかっている(係数がa)」と考えることが出来る。
x0は必ず1が入力されるものと考えると、bの項は
y = a_1x_1 + a_2x_2 + a_3x_3 + a_0x_0
として表現できる。
推定するための式「y=ax + b」を探すには?
推定式は「モデル」とも呼ばれる。
良きモデルを作るとはどういうことか?
「推定値が実際の値と"あまり"外れないこと」
人工的に作ったモデル
「y(推定) = ax + b」
と、
データで実際に得られている「y」の差
「y - y(推定)」
が小さければ、良きモデルと言えるのではないだろうか。
この話が最小二乗法と呼ばれる問題である。
最小二乗法
高校数学の美しい物語-最小二乗法
がわかりやすい。
図はリンク先で見てもらうとして、
「実データのy」と「推定式から得られるy(推定)」の組み合わせの差の合計を最小にする。
\sum (y - y(推定))^2
二乗にしているのは、距離を計算するために強引に二乗していると考えてください。
(推定式からデータ点の差は「+と-」があり、単に合計すると0になる)
\sum
(y - (a_1x_1 + a_0x_0) )^2
とも書ける。
この式を解くためのy,x1,x0はすべて用意されている。
y,x1は実データのy,x(身長,体重)の値であるし、
x0は常に1である。
となると求めるのは
a_0と
a_1
この二つのパラメータを求めることで、推定式を得ることができる。
求め方
求め方は各パラメータに対する偏微分で求められる。
\sum
(y - (a_1x_1 + a_0x_0) )^2
をa0に対して偏微分してやると、(y - y(推定))を最小にするための「a0」が求まり、
a1に対して偏微分したらa1が求まる。
問:最急降下法って何?
解:関数内のパラメータの最適化問題に使われるアルゴリズム
最急って言葉は最速とか特急とかいう意味ではなく、
最も勾配が急な方向に降りていくという意味。
(微分した時の傾きが急な方向に更新される)
パラメータの最適化には偏微分を用いる。
偏微分や合成関数の計算過程についてはここでは触れないが、
パラメータを求めるには
a0偏微分=-2\sum x_0(y - (a_1x_1 + a_0x_0) ) = 0\\
a1偏微分=-2\sum x_1(y - (a_1x_1 + a_0x_0) ) = 0
を解いていけば良い。
実際に作成
まずデータを作成する。
真のパラメータa0,a1から生成した値yを作成
a0_true <- -5
a1_true <- 2
data_x <- runif(300, -5, 5)
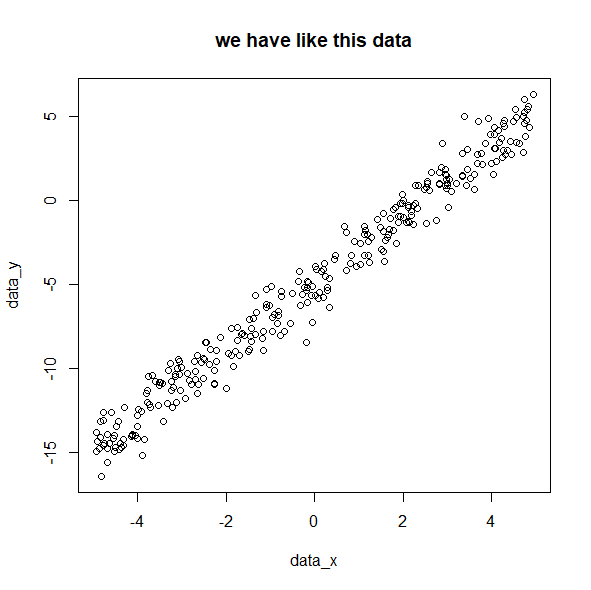
data_y <- a0_true*1 + a1_true * data_x + rnorm(300)
plot(data_x, data_y,main="we have like this data")
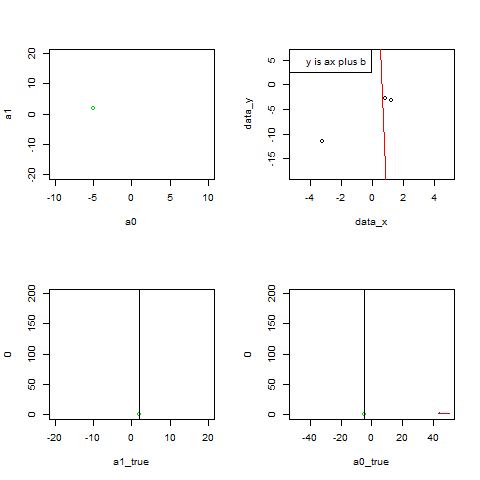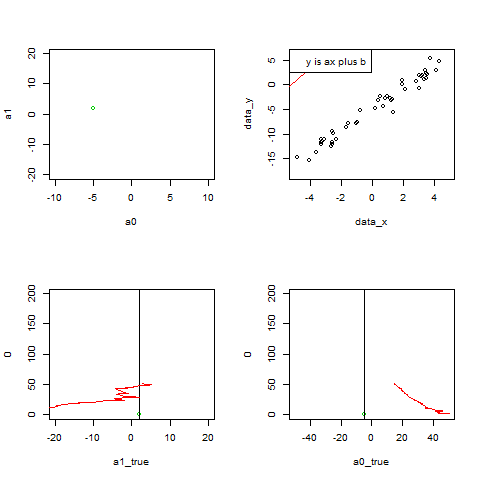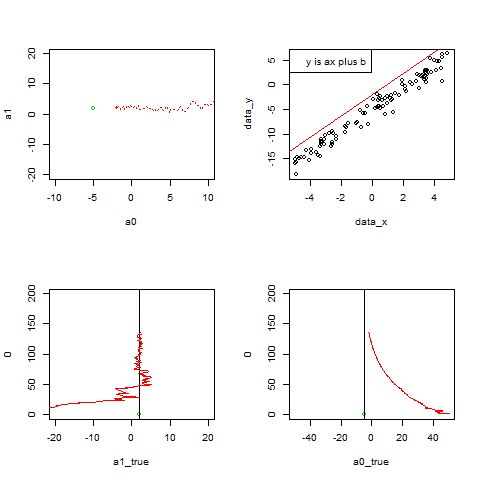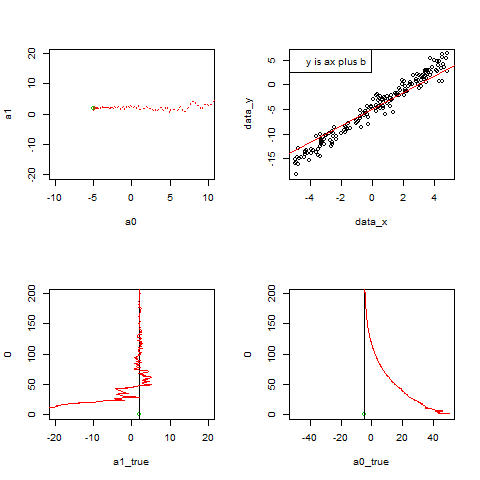
y = -2x -5 が求めたい式。
これを下の最急降下法で求められたら成功
大変に雑な話をするが、最初に適当にa0,a1というパラメータを決めて、
推定式をつくってしまう。
a0_init <- 50
a1_init <- -100
# y = 50*1 -100*x
適当に決めた値をa0,a1という変数に代入する
a0 <- a0_init
a1 <- a1_init
図をplotするための変数をNULLにしておく
a0list <- NULL
a1list <- NULL
p <- NULL
x_box <- NULL
y_box <- NULL
学習率を用意
学習率に関しては以下で説明。
eta <- 0.01
for文の中を分解して解説
inum <- sample(300, 1)
xi <- data_x[inum]
yi <- data_y[inum]
先ほど発生させた300個のデータをランダムで1つ取り出す。
a0_new <- a0 - eta*(2*1 *(a0 + a1*xi - yi))
a1_new <- a1 - eta*(2*xi*(a0 + a1*xi - yi))
偏微分によって得られたパラメータの更新式にx1とy1を代入する。
データyと推定のyの差を計算し、最初に設定したa0,a1から引く。
パラメータの傾きが真の傾きよりも大きければ、推定値は大きくなってしまう。
そのため、パラメータの傾きを小さくしなければならないので引き算をする。
推定値が実データよりも小さい場合、y-yは負の値になる。
この場合、傾きが負に傾き過ぎているという事なので、傾きを正の方向に修正する必要がある。
そのため、負×負が正になり、パラメータに足される。
切片に関しても同じ。
etaは学習率という。
修正を行うとき、そのままy-yの値をパラメータから引くと、影響が大きすぎるため、
学習率という値で影響度を調節している。
パラメータを更新する。
変化の様子をplotするためlistに入れる。
a0 <- a0_new
a1 <- a1_new
a0list <- c(a0list, a0)
a1list <- c(a1list, a1)
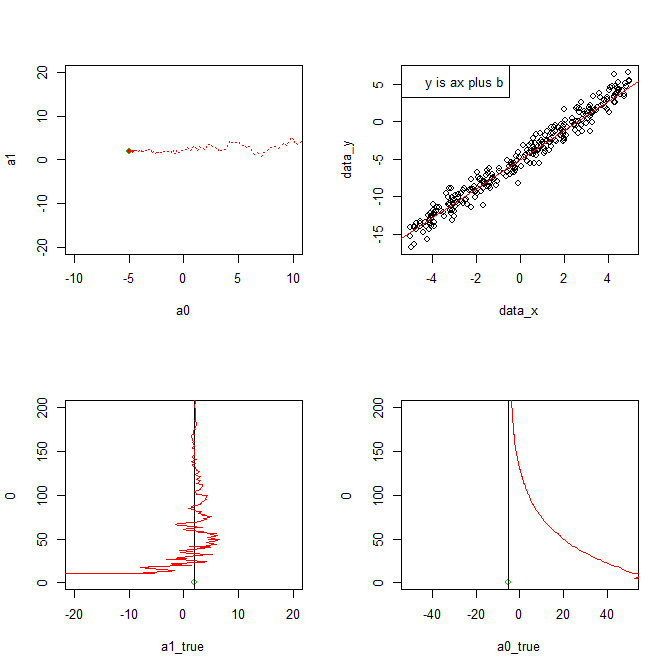
設定した真のパラメータに向かっていく様子を書き込む
par(mfrow=c(2, 2))
plot(a0, a1, xlim=c(-10, 10), ylim=c(-20, 20), pch=20, col=2)
points(-5, 2)
points(a0, a1, col=2, pch=20)
points(a0list, a1list, col=2, type="l", lty=3)
points(a0_true, a1_true, col=3)
取り出してきた実データが徐々に増え、
最小二乗法によって求まる直線がデータにフィットしていく様子を描く。
x_box<-c(x_box, xi)
y_box<-c(y_box, yi)
plot(data_x, data_y,type="n")
points(x_box,y_box)
abline(a0, a1, col=2)
legend("topleft",legend="y is ax plus b")
パラメータa1の変化をplot
p <- c(p,length(a1list))
plot(a1_true, 0, xlim=c(-20, 20), ylim=c(0, 200), col=3)
abline(v=a1_true)
points(a1list, p, col=2, pch=20,type="l")
パラメータa0の変化をplot
plot(a0_true, 0, xlim=c(-50, 50), ylim=c(0, 200), col=3)
abline(v=a0_true)
points(a0list, p, col=2, pch=20,type="l")
これをfor文を使ってデータを取り出して更新させて、を繰り替えす。
以上
コード
a0_true <- -5
a1_true <- 2
data_x <- runif(300, -5, 5)
data_y <- a0_true*1 + a1_true * data_x + rnorm(300)
plot(data_x, data_y,main="we have like this data")
a0_init <- 50
a1_init <- -100
# y = 50*1 -100*x
a0<-a0_init
a1<-a1_init
a0list <- NULL
a1list <- NULL
p <- NULL
x_box <- NULL
y_box <- NULL
eta <- 0.01
for(i in 1:400){
# png(paste0(i,".png"))
inum <- sample(300, 1)
xi <- data_x[inum]
yi <- data_y[inum]
a0_new <- a0 - eta*(2*1 *(a0 + a1*xi - yi))
a1_new <- a1 - eta*(2*xi*(a0 + a1*xi - yi))
a0 <- a0_new
a1 <- a1_new
a0list <- c(a0list, a0)
a1list <- c(a1list, a1)
par(mfrow=c(2, 2))
plot(a0, a1, xlim=c(-10, 10), ylim=c(-20, 20), pch=20, col=2)
points(-5, 2)
points(a0, a1, col=2, pch=20)
points(a0list, a1list, col=2, type="l", lty=3)
points(a0_true, a1_true, col=3)
x_box<-c(x_box, xi)
y_box<-c(y_box, yi)
plot(data_x, data_y,type="n")
points(x_box,y_box)
abline(a0, a1, col=2)
legend("topleft",legend="y is ax plus b")
p <- c(p,length(a1list))
plot(a1_true, 0, xlim=c(-20, 20), ylim=c(0, 200), col=3)
abline(v=a1_true)
points(a1list, p, col=2, pch=20,type="l")
plot(a0_true, 0, xlim=c(-50, 50), ylim=c(0, 200), col=3)
abline(v=a0_true)
points(a0list, p, col=2, pch=20,type="l")
# dev.off()
}