闇の魔術に対する防衛術 Advent Calendar 2020の三日目
はじめに
データの可視化は非常に難しい。
まずデータの抽出が難しい
・データソースごとの整合性が取れているか
・取得したデータとソースデータに欠損が生じていないか
・SQL文を実行したサマリの結果が部分的に抜け落ちていないか。
その確認は時間的にも精神的にも苦痛。
しかし、苦労して抽出したデータも使い方で全くの無駄になる
その例として「可視化や統計」部分に着目してお話をしようと考えた。
データの背景を知らない人には、データ可視化が歩み寄る手段になるし、伝えたい事をインパクトを伴って伝えられるなど非常にメリットである。
※ただし
「可視化」の使い方によっては誤った理解をさせることも可能。
伝えたい事だけを正しいように見せる方法もあり、
可視化に詳しくない人に誤解を与えて自分の主張を通すこともできるかもしれない。
これは闇の魔術に深く関係しているに違いない。
悪意はおそらく,きっと,多分,無いと思うが、いくつかの怪しいレポートを発見する機会があったので、その内容を紹介する。
今まで出会った闇の魔術を紹介することで、自身が闇の魔術を使わない&使われたときの防衛術に活かしてほしい。
3D円グラフでの闇の魔術:1
これは既に有名な闇の魔術だと思う
この角度から見た時、どのカテゴリが一番大きいように見える？
灰色？
こちらの角度からは、「オレンジ」のカテゴリと答えるかもしれない。
実際には灰色とオレンジ色のカテゴリは数値的に5%の違いしかない。
しかし、人間の目は立体や周囲の配色によって錯覚を受けやすい。
3Dにすることで印象は変わる
さらに色がついていれば膨張色や背景との対比で尚のこと
今回の件から得るべき教訓は、
本当に伝えたいことは各カテゴリの割合であり、錯覚を利用して印象操作をしてはいけない。
2D円グラフでの闇の魔術:2
3Dでない円グラフも同じ。
このグラフからどのカテゴリが一番大きいか判別できるだろうか？
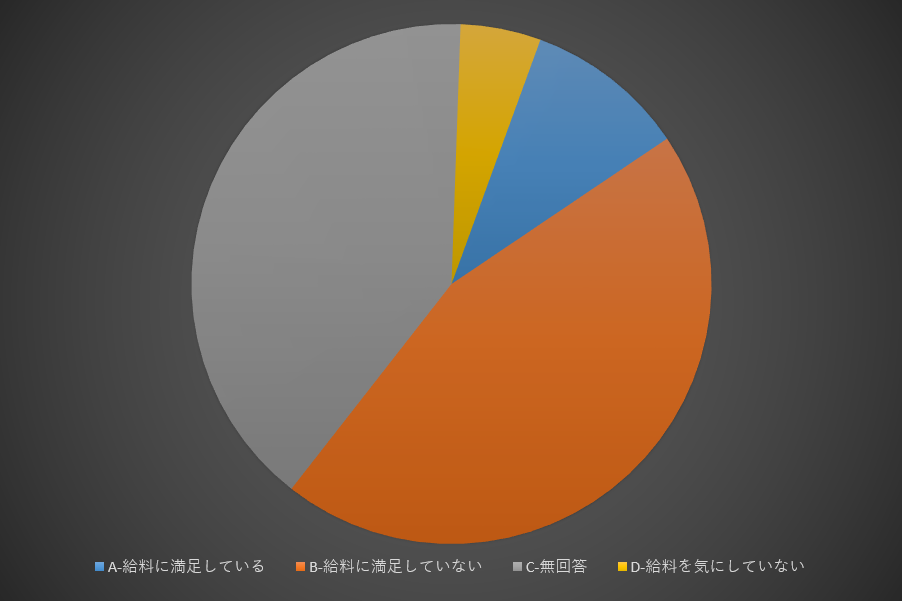
数字がついていれば判別できる？
つまり数字がついていなければ理解できないという事は、この可視化には意味がない。
どのカテゴリが一番高いのかが分かりやすく、他のカテゴリとの比較もしやすい
もちろん縦軸の値はつけておくのが親切なので、さらに修正して下図のようにする
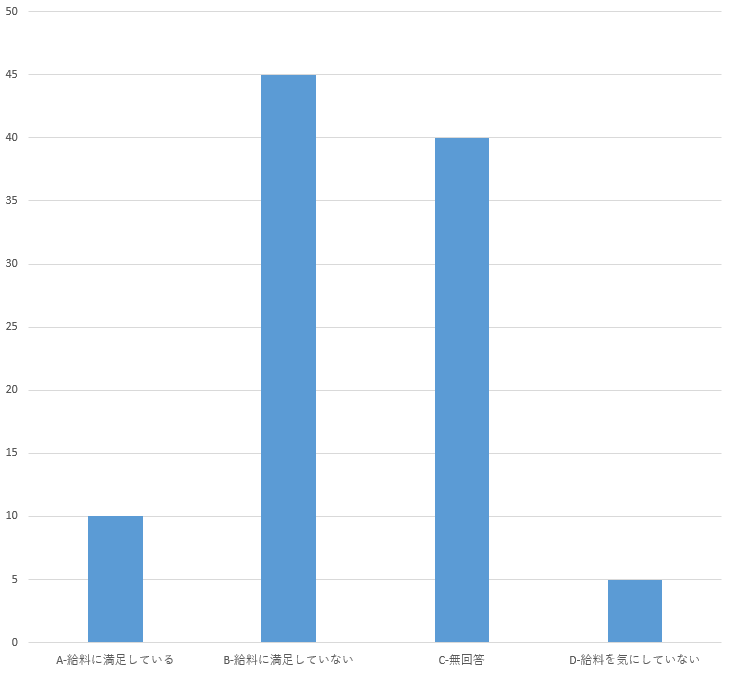
今回の件から得るべき教訓は、
比較したい対象を色分けする必要があるのか十分に考える。視覚的に「差の情報」が伝わるグラフを選択する。
x軸ラベルの闇の魔術:3
私自身はグラフ描画の都合上気にせずx軸ラベルの90度回転など実行してしまうのですが、
軸ラベルの回転は初めてこの結果を見る人にとって少々理解の妨げになるようです
そのため、ラベルはなるべく読みやすさを意識しましょう
今回の件から得るべき教訓は、
データを初めて見る & その図と向き合う時間が短い そんな人でも理解できる図を作る事を意識したい
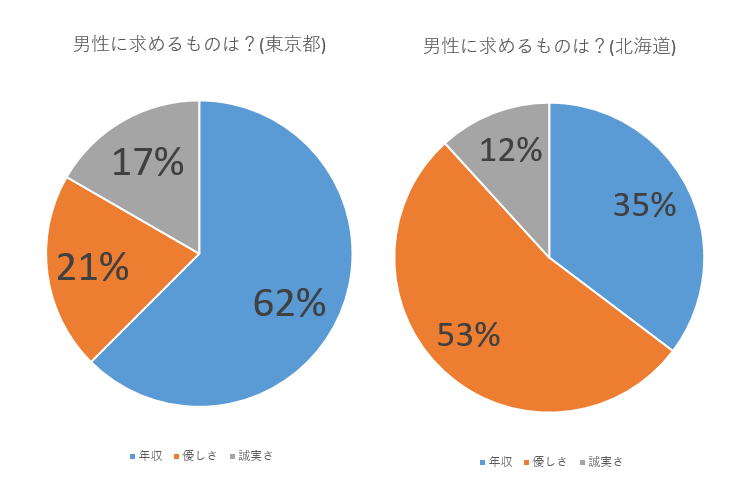
割合を示すための闇の魔術:4
こんなグラフがあったとしよう
数字もついているし、平面の円グラフだし、どのカテゴリが一番大きいか知ることはできる。
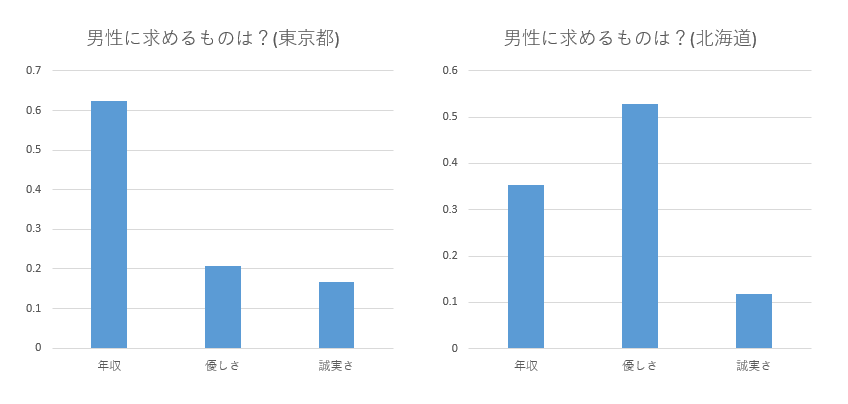
円グラフが問題アリという話をしたばかりなので棒グラフにしてみよう
これでだいぶマシになった。
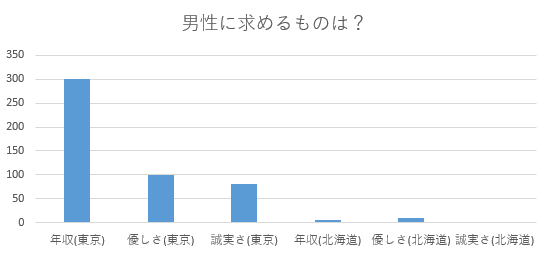
東京の女性はどうやらリアリストが多いみたいだし、年収に自信がないから北海道への移住を決めようかな。
と思った人は一度待っていただきたい。
割合とはあくまでも全体に対するカテゴリの比率なわけで、
パーセントと出ていたら「全体数」を気にしなければいけない。
つまり分母が小さければパーセントはいくらでも大きく見せることができる。
このデータは以下ような集計結果から作ったものである。
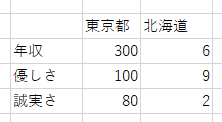
数字に強い(と一括りにすると怒られるが)エンジニアの皆様は割合には踊らされないと思うが、周囲に誤解を生まないためにも正しい図は作成したい。
今回の件から得るべき教訓は、
割合を図で扱う時には全体数も明記する (いわゆるサンプルサイズ)
割合を示すための闇の魔術：別の防衛術
割合に直さなければデータの不均衡さに気づくことができる
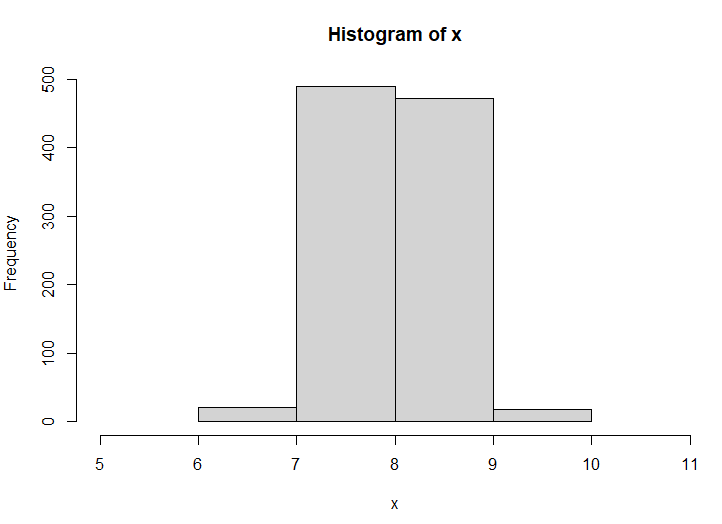
ヒストグラム幅の闇の魔術：その1:5
謎の安全な白い粉を袋に入れる仕事をしているとする
一つの袋は8gで売っている
上司から、最近消費量が多い気がするので入れすぎていないか？と聞かれてはかりでデータを取り始めた
非常にg単価の高い粉である
データを取った結果、ばらつきである標準偏差を調べsd = 0.5であったことを報告した
ついでにヒストグラムにして報告しよう
きっとこの図を見せたらよくやっていると褒められるに違いない
このグラフの欠点は
「g単価が非常に高い商品なのに、g単位でしか測れない測りを使ったこと」
もしくは
「ヒストグラムの幅をg単位に設定してしまったこと」
にある。
データは意味を持っている単位で集める必要がり、微小の変化が重要になる時に大雑把なデータを取得しても仕方がない
幅を大雑把にしても同じく伝えたい情報が伝わらない
そんな図に意味はなくなる
今回の件から得るべき教訓は、
ヒストグラムの幅、データの単位は示したい情報を適切に示せる幅(単位)に設定する
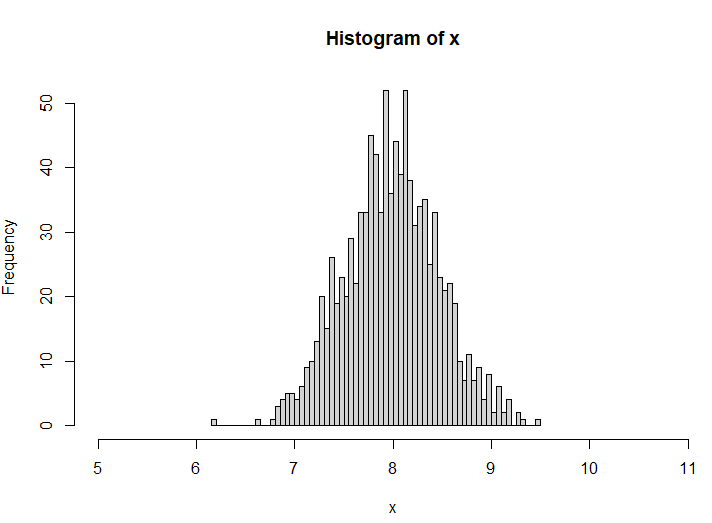
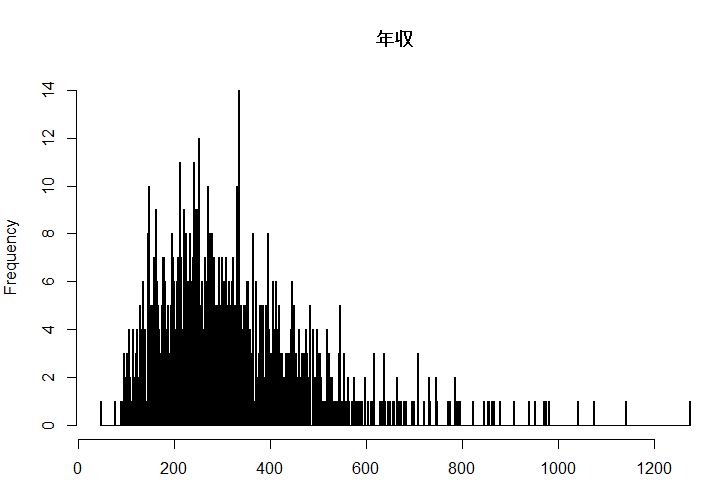
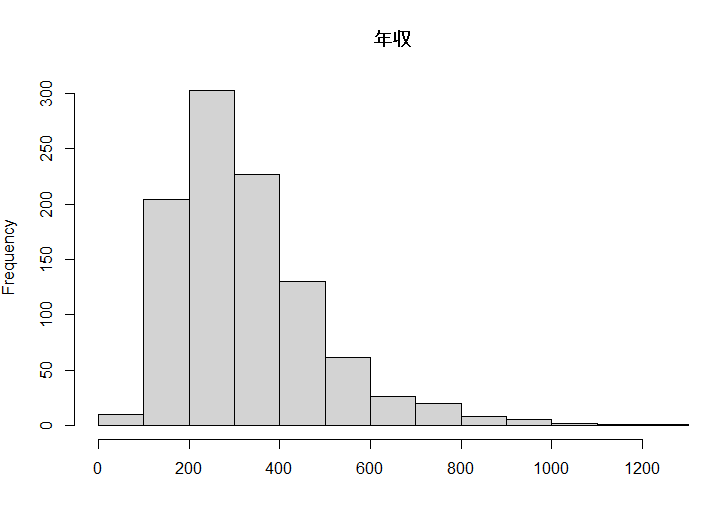
ヒストグラム幅の闇の魔術：その2:6
逆に細かい事による無意味さも出てくる
例えば年収をヒストグラムにする
こんなに一人ひとりの小さな違いを可視化しても全体の傾向がわからない
年収は50万,100万の単位で議論されることが多い理由も、細かい値は誤差で情報がなくなってくるから
(もちろん細かい数値について議論したい場合にはこの幅でもいい)
今回の件から得るべき教訓は、
細かくしすぎると、不要な情報で混乱させることもある
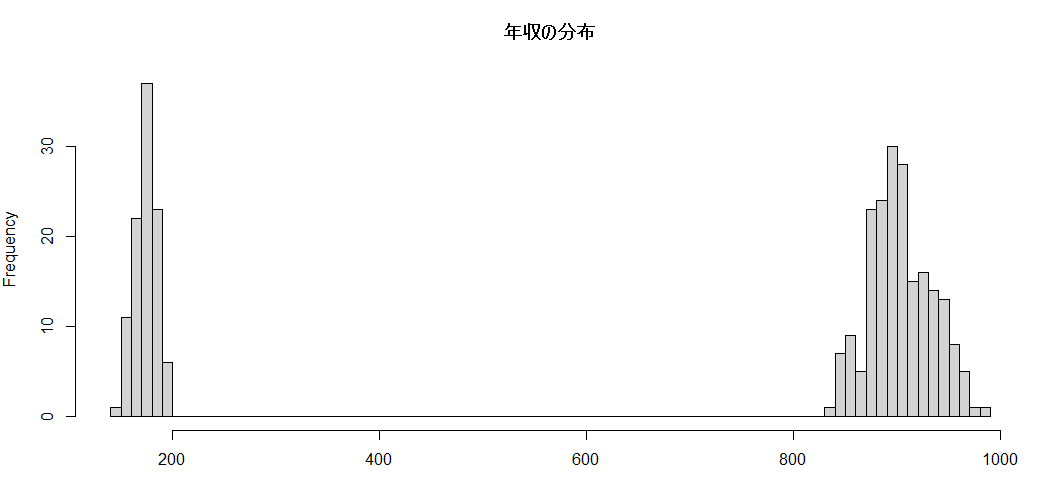
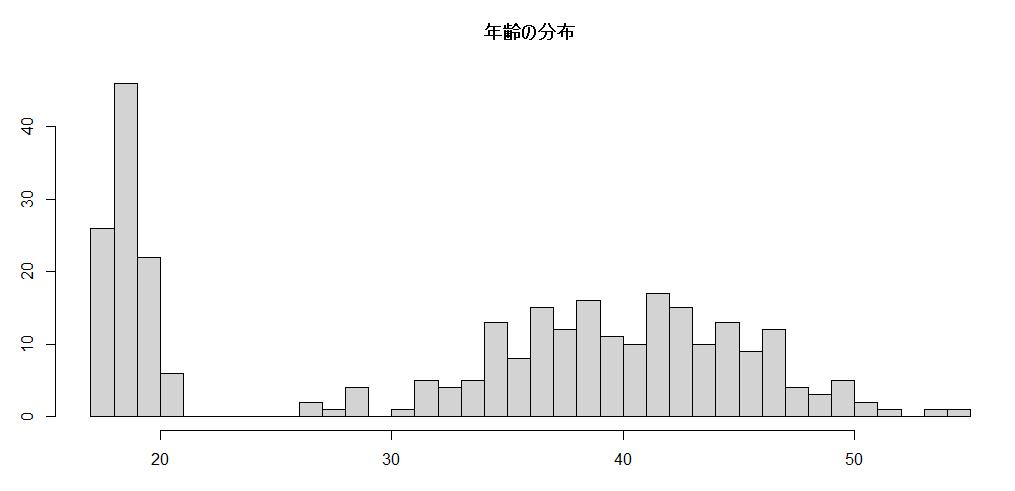
都合の良い統計量だけを見せる闇の魔術:7
この会社の平均年収は660万円です
この会社の平均年齢は33歳で若手が活躍しています
大変にチャレンジングで面白そうな会社ではないか?
平均というのはあまりロバストでない統計量なので、大きい値・小さい値に対して影響を受けやすい。
さらに、言葉のイメージから「中心」というイメージを持っている人も多いかもしれないが、
中心の意味するのは「やじろべえのバランス点」であり、
大きい値と小さい値がフタコブ状にバランスを取っていれば平均年収をもらっている人がいなくても「平均年収」が出てくる。
誰が従業員として入っても利益の出るような完成したビジネスモデルの上では年齢や年収の分布に偏りが出ることも多い。
今回の件から得るべき教訓は、
統計量だけで情報を鵜吞みにしない、数値だけでなく公開できる範囲で真実を図にする
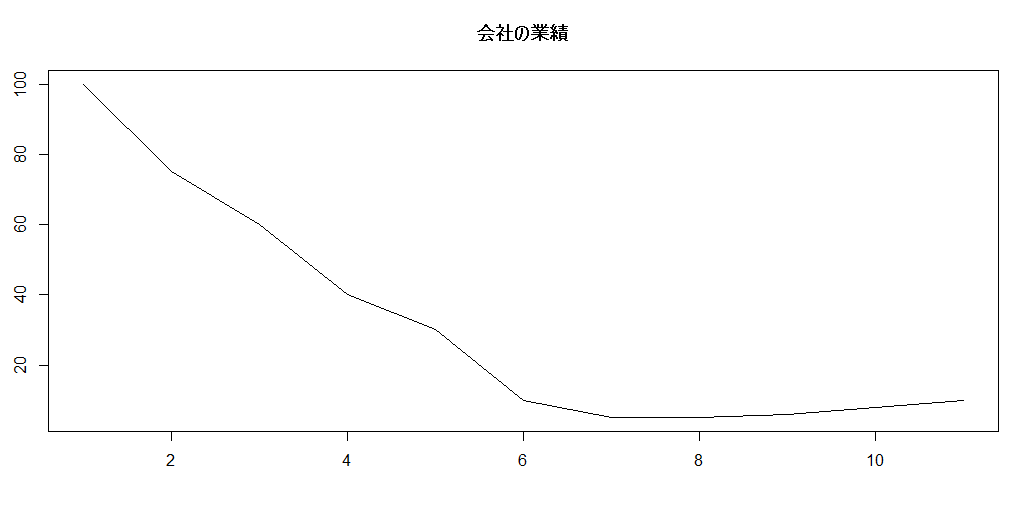
軸のスケールを使った闇の魔術：その1:8
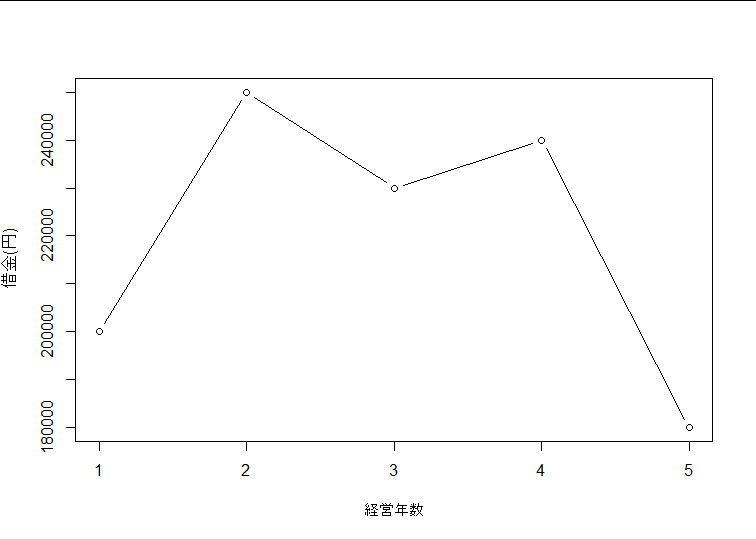
最近、わが社の借金が急激に減った
そういわれるとそう思えてしまう
特に一瞬の報告資料などでは気づけないこともあるかもしれない
図は正しく情報を伝えるべきであって、ミスリードを誘発するのは良くない
ただし、既にこの範囲で値を監視すると合意を取っている上での報告なら悪くない。
問題なのは勘違いする図を見せることで、受け手が正しく理解できる状況ならばスケールはこのままでもいいかもしれない。
しかし、この範囲に固定した場合、180000以下の値が表示されなくなってしまう。
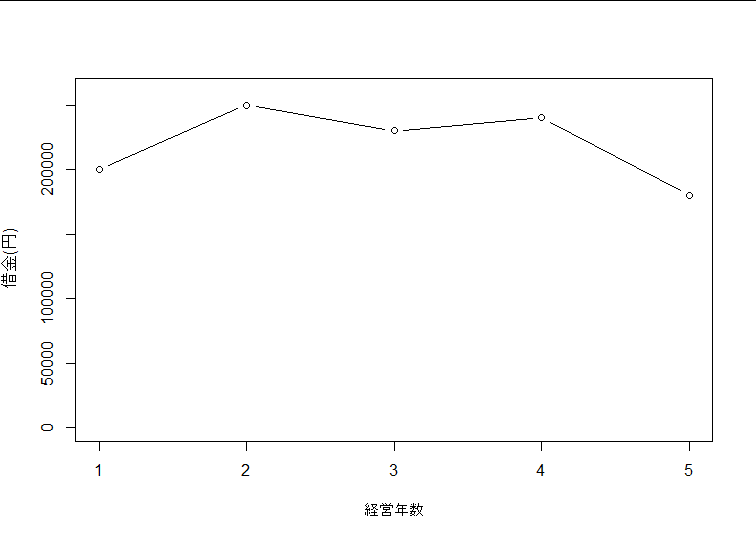
どのグラフにも言えることだけど縦軸は0から始まるスケールで表示するのが無難
今回の件から得るべき教訓は、
数値のスケールは伝わりやすく、変化量を過剰に見せつけない
軸のスケールを使った闇の魔術：その2:9
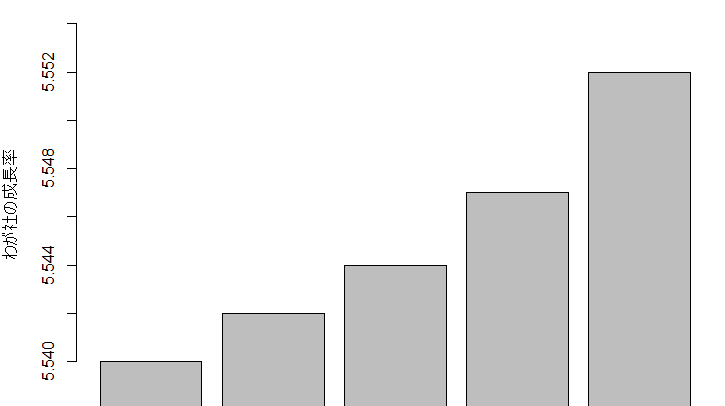
小さいスケールにも注意
小さいスケール幅をy軸に設定したことによって、数値は同じなのに大きな変化に見える。
本来伝えるべき尺度でグラフ化すること。
今回の件から得るべき教訓は、
微小の変化に意味が無いのならば正しいスケールで見せること
軸のスケールを使った闇の魔術：その3:10
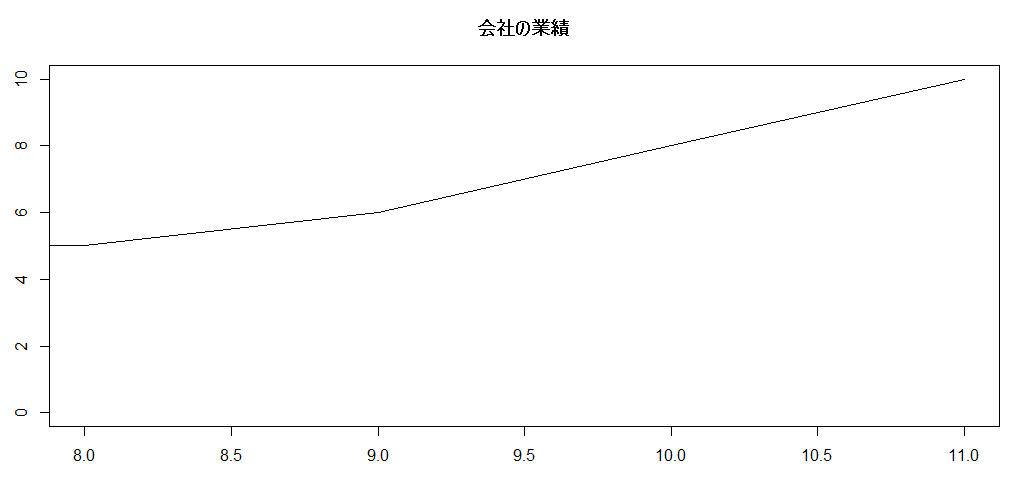
横軸についても言える。
時系列を見せて、x軸は都合の良い最近の期間だけを見せておく。
一部分だけ切り出した場合、そのy軸のスケールが0始まりで正しいように見える
ただし、過去のx軸の情報を含めた場合見え方は変わる
今回の件から得るべき教訓は、
伝えたい情報や保身のために恣意的な区間を選んではいけない
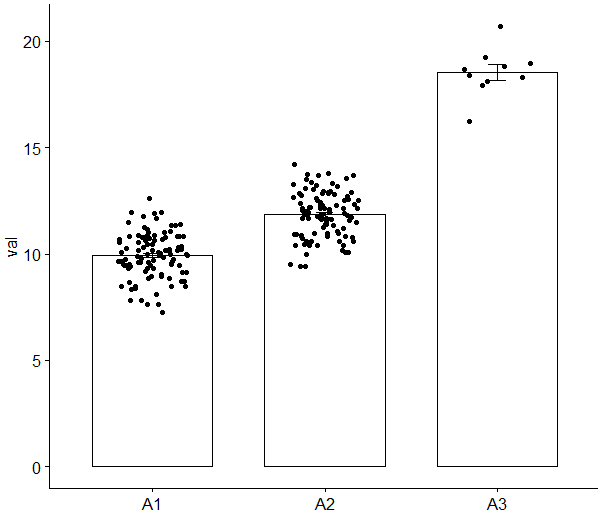
偶然誤差を隠す闇の魔術:11
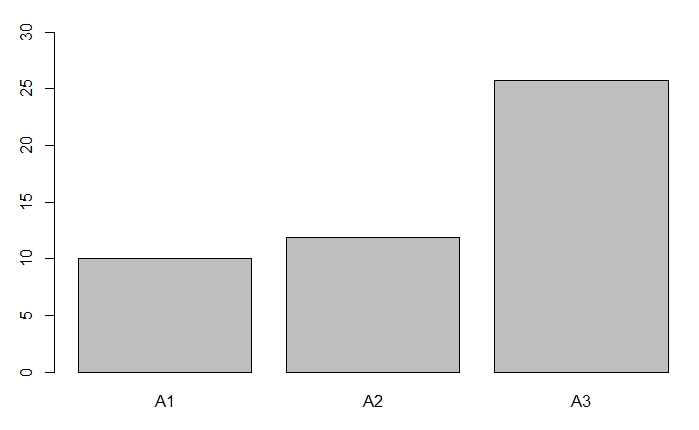
広告A1~A3までを試した結果、A3が非常に効果が高いようです
これ以降A3を使っていきます！
しかしデータのバラツキを確認してみると、A3はかなりバラツキが大きい。
これでは、「実はA1,A2とA3は変化が無いが、たまたま今回は変化が出たように見えた」という可能性が残る。
そこでバラツキの範囲も付け加えておくのが親切
今回の件から得るべき教訓は、
統計量はばらつきも加えて説明する。加えて比較用の検定もあるので、これを使う
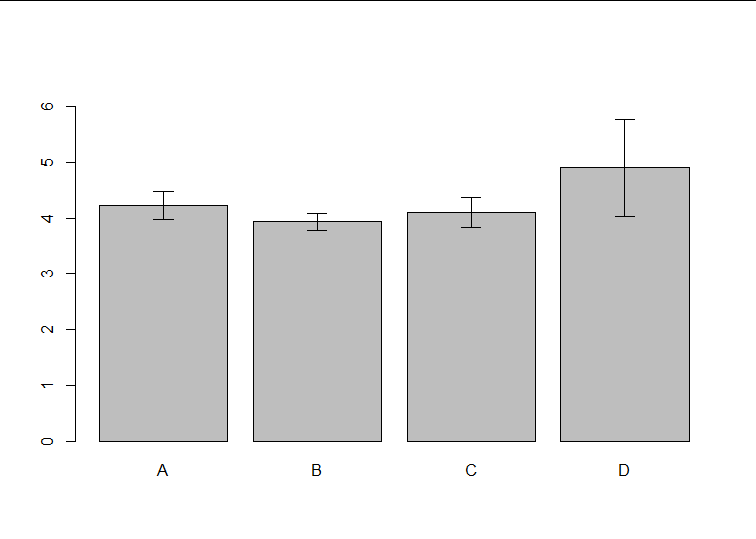
データの偏りを隠す闇の魔術:12
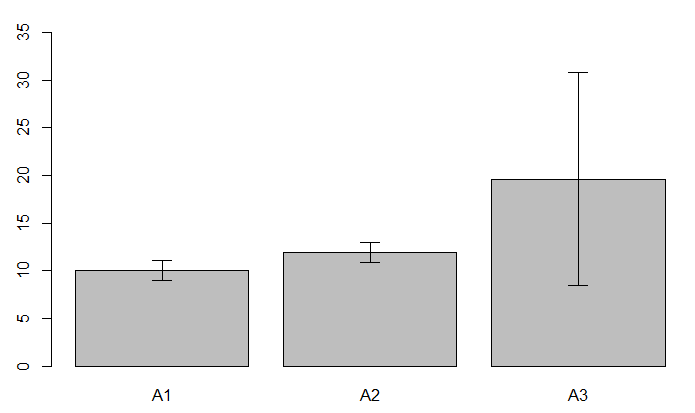
エラーバーも付けました。
バラツキも非常に小さいことがわかりました。
これでA3の広告にしてもいいですよね？
先にも出ましたが、サンプルサイズが不明な状態の「割合,平均,中央値」などの統計量はなんとも信用ができません
データの「密度やサイズ」を確認できるように補助するのが適切でしょう
この結果を見て、A3の信頼性が担保できるでしょうか？
少数の中でたまたまバラツキが小さく、たまたま大きい平均値が観測されただけと判断できてしまいます
今回の件から得るべき教訓は、
サンプルサイズは他のグループと同等で比較できるようにし、その情報も確認できるようにする
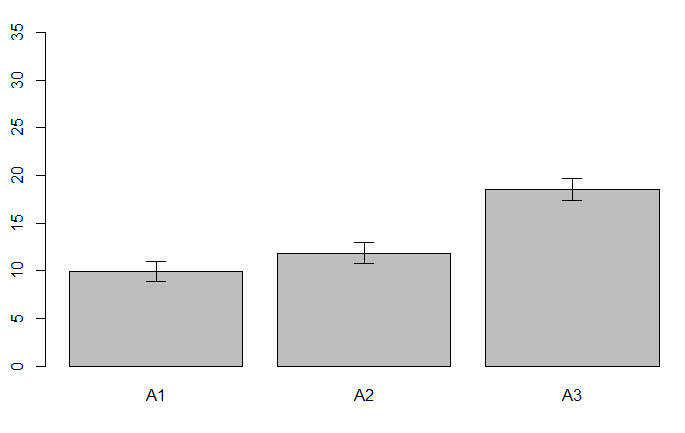
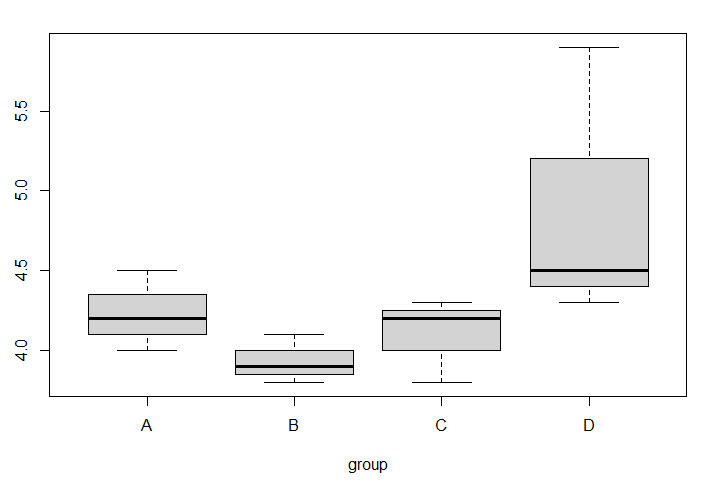
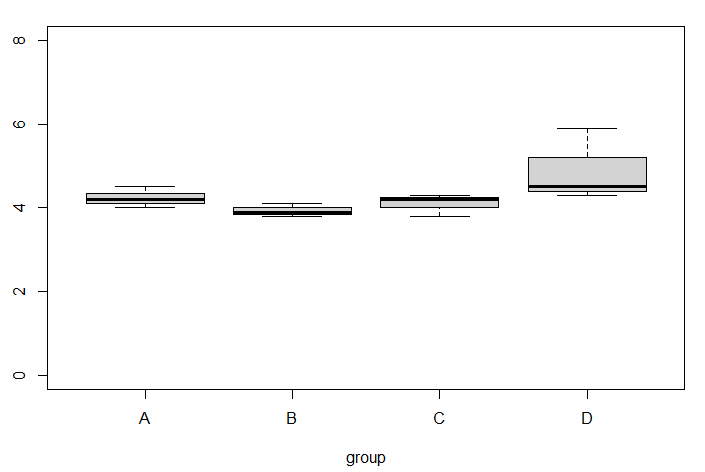
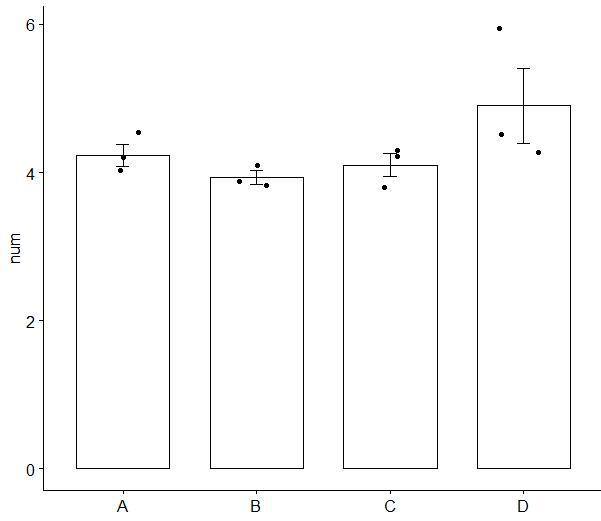
データ不足のデータを使った闇の魔術:13
新製品を開発した。
従来品Aに比べてDの値が上がっているので、開発は成功です
おなじデータで箱ひげ図を作ってみる
やはりDの値が他のグループよりも大きく見えます。
なにか問題がありそう？？？
気づいてもらえたと思うが、これはy軸の値任意に変更されているので
図に惑わされてしまうかもしれない
y軸の値を整えると
整えたとしても、やはりDグループが大きいように見える
既に例に出した闇の魔術を組み合わせただけの例
サンプルのサイズも小さいし、バラツキが信用できないデータだった
今回の件から得るべき教訓は、
十分なデータが無いことも併せて表示したい
ただ、実験と倫理の板挟みにあるような生物実験の分野では1グループn=3のような実験が行われることもある
あくまでも臨床よりずっと前の段階の実験論文であったり、速報誌で見る。
その場合には厳しめの有意差検定が行われている場合が多い。
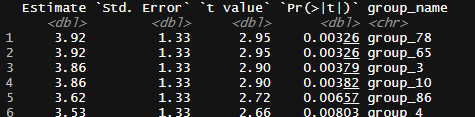
偶然誤差を発見とみなしてしまう場合:14
頑張り屋の後輩が入社してきて、webサイトのユーザー一人当たりの購買金額を向上させようと頑張っている。
「100個新しいwebサイトのデザイン作ってきました。テストした結果、4つほど現状のサイトよりも統計上有意な差が見つかりました！」
とっているサンプルサイズも別に問題は無さそうだが...
そもそも統計的に有意かどうかを確認する際、
「滅多に起こらない値が取れたかどうか」
を基準に判定している。
100個もサイトを作って試したら100個中1個や2個はたまたまユーザーの購買タイミングが重なることなどあるでしょう
実際、この100のデータは全く同じパラメタの母集団からサンプリングしてきた結果です
今回の件から得るべき教訓は、
「とりあえず」で沢山の比較対象に対して有意差検定を行ってはいけない (多重比較)
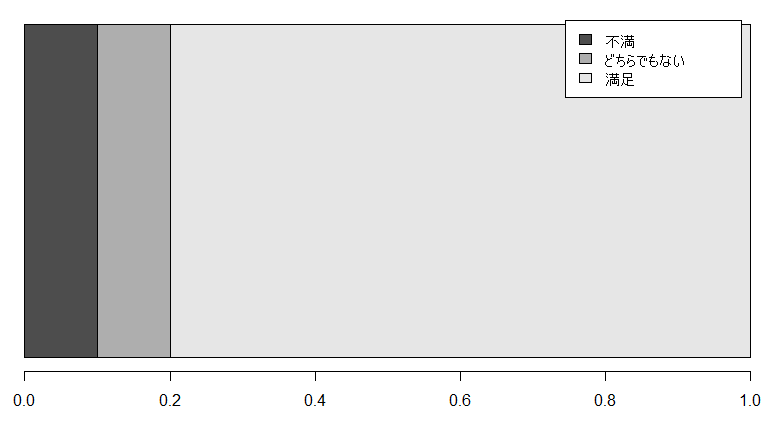
偏った質問項目と集計を使った闇の魔術:15
あるレストランに行ったときにアンケートを取られた
その後、再びレストランに向かうと
80% の方が満足と回答したレストランです
と書かれた看板が立っていた。
どのようにデータを集めたのか、どのように集計を行ったのか見えない場合には判断つけようがないが、
これを資料として見せられ、この範囲から情報を何とか理解しようと努めてしまうと誤解が生まれる。
今回の件から得るべき教訓は、
データ収集時のアンケート項目の公開、集計方法は恣意的なまとめ方を行わない
こういうアンケートの日に限って過剰にサービスが良かったりする。
情報操作のためのアンケートはひっそりはびこっている闇。
報告される側は鵜吞みにしてはいけない。
【アンケートなんてするな】効果検証のためのアンケート分析本10冊読んだので書評書く。
偏ったアンケート対象を使った闇の魔術:16
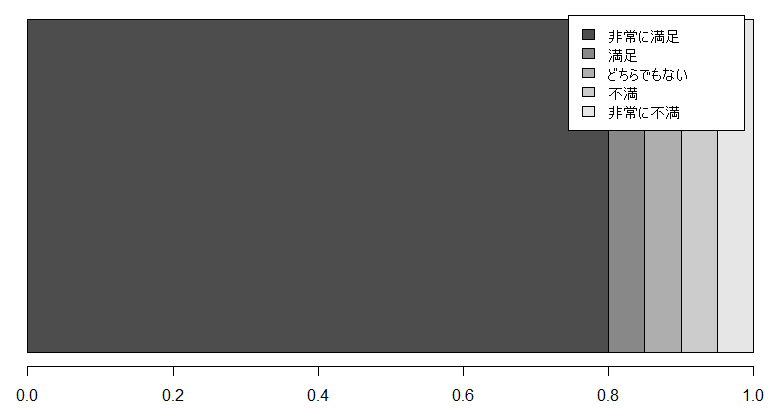
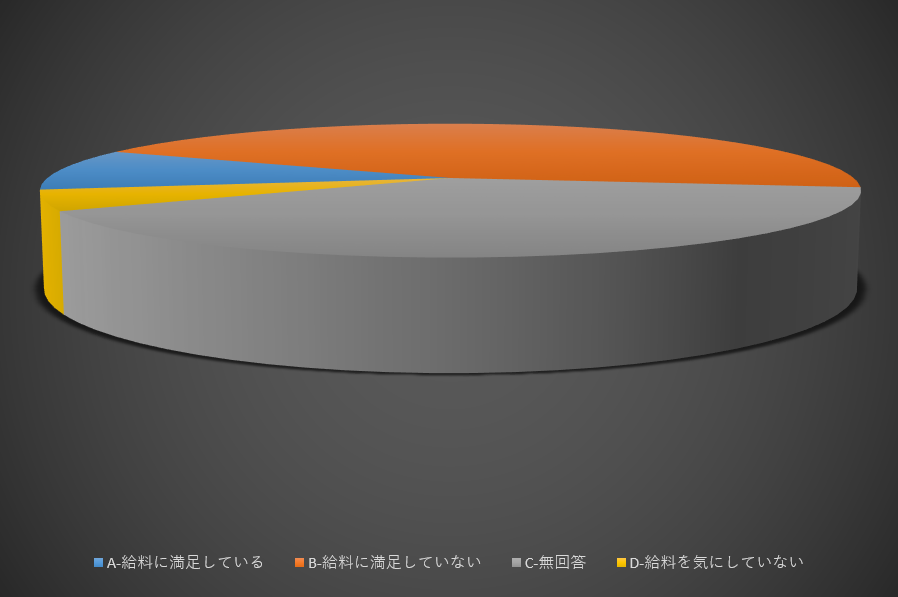
ある会社の説明会で以下の資料が公開されていた
当社は80%の社員が給料に満足しています
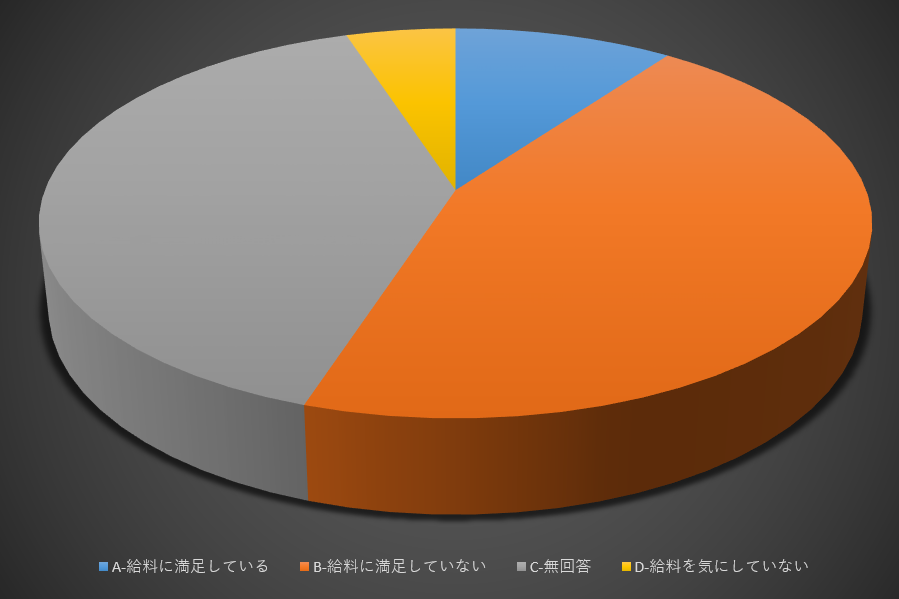
質問項目や集計が偏っていたのかと思い、項目を確認させてもらった
どうやら質問項目と図の項目数も一致しているし、偏った質問だけでもなさそうだ。
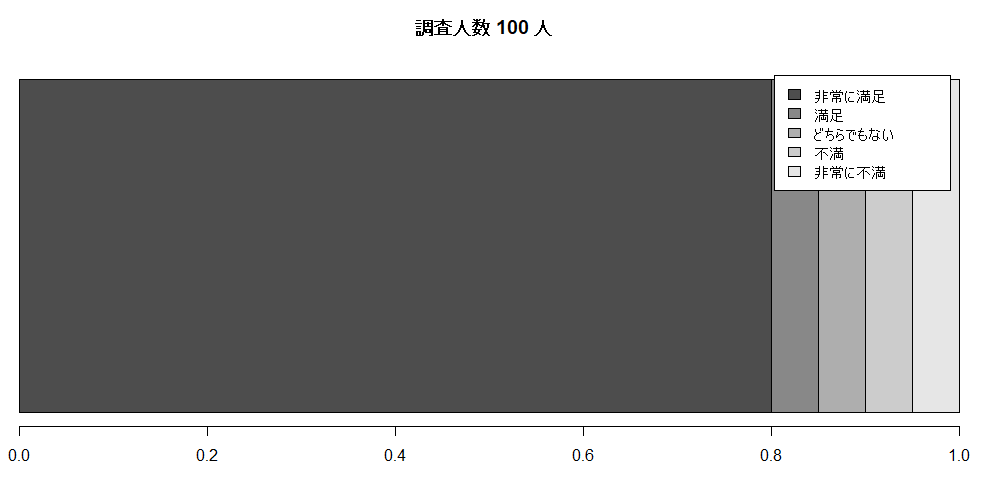
では人数が少なかったのか？
調査人数は100人取っているようだし、怪しさが分からなくなってきた。
会社の規模が100人の会社ならば全員の回答だから真実だろう。数万人の会社であった場合には100人程度の調査ではばらつく可能性もある。
バラツキの原因とは？
調査対象者の詳細を確認させてもらうと、
※40代以上、オフィス勤務のマネージャー職への質問
ということが分かった。
つまり、「社員の満足度」ではなく、正しくは「マネージャー職に任命された人たちの満足度」になる。
調査対象に偏りがあった場合、集計以前に結果が偏ることがある。
今回の件から得るべき教訓は、
調査対象の詳細を公開して、報告資料の説明を「当社」という大きな対象に設定しないこと (サンプルセレクションバイアス)
以上
紹介した内容は参考になりましたか？
しかし、この記事の内容もあまり信じないでください。
だって私も勉強不足から「闇の魔術」を使ってしまうので...
その他
関係があるように見えてしまうグラフ：Spurious Correlations
見せかけの関係性、因果ではない：原因と結果の経済学
グラフでうそをつく方法、捉え方でどのようにも図をつくることができる例が面白い:gigazin
分と秒を別で記述すると過剰な差を表現することができる
遠近法を使うと数値とイラストが一致しなくなる：Lie_Factor
WHOのグラフ、縦軸が無いので割合の値とグラフがあっていない
おなじような趣旨の記事：Lessons on How to Lie with Statistics
How to Lie with Statistics
A Quick Guide to Spotting Graphics That Lie