3軸リアクションホイール倒立振子を作るアドカレの21日目です。
前回(Day 20)までに、3軸姿勢推定の手法として「拡張カルマンフィルタ(EKF)」と「Madgwick(マドウィック)フィルタ」の2つを実装しました。
- Madgwickフィルタ: 計算コストが非常に低く、ドローン制御などのデファクトスタンダード。
- EKF: 計算コストは高いが、確率統計的にノイズを最小化する厳密な推定が可能。
今回は、この2つのアルゴリズムをSTM32G474上で同時に動作させ、「計算負荷(処理時間)」と「推定精度(静特性・動特性)」を定量的に評価します。
どちらが優れているかという単純な優劣ではなく、「本プロジェクトのハードウェア構成(STM32G474 + 6軸IMU)において、どちらを採用すべきか」という技術選定のプロセスを共有します。
1. 評価環境とアルゴリズムの概要
比較を行うにあたり、以下の条件で実装を行いました。
- MCU: STM32G474 (170MHz, FPU有効)
- Sensor: ICM-42688 (6-Axis IMU, 加速度+ジャイロ) ※地磁気なし
- 制御周期: 10ms (100Hz)
各フィルタの特徴
-
Madgwickフィルタ
Madgwickフィルタは、観測された重力加速度 $a$ と、現在の姿勢 $q$ から予測される重力方向の誤差関数$f(q, a)$ を定義し、その誤差が最小になる方向へ勾配降下法(Gradient Descent)で姿勢を更新します。
$$\nabla f = J_g^T(q) \cdot f_g(q, a)$$
$$q_{k+1} = q_k - \beta \frac{\nabla f}{||\nabla f||} \Delta t$$
ここで $J_g$ は誤差関数のヤコビアンです。このアルゴリズムは逆行列計算を含まないため、計算量は $O(1)$ であり、極めて軽量です。 -
拡張カルマンフィルタ (EKF)
EKFは、非線形なシステム方程式を偏微分(線形化)して扱います。特に計算負荷の大部分を占めるのが、クォータニオンと重力ベクトルの関係を示す観測モデル $h(x)$ の線形化、すなわち ヤコビ行列$H$ の計算と、それに続くカルマンゲインの導出です。
観測行列 $H$($3 \times 4$ 行列)は以下のように記述されます。
H = \frac{\partial h}{\partial q} = 2 \begin{bmatrix} -q_2 & q_3 & -q_0 & q_1 \\ q_1 & q_0 & q_3 & q_2 \\ q_0 & -q_1 & -q_2 & q_3 \end{bmatrix}
さらに、この行列を用いて以下のカルマンゲイン
$$K_k = P_{k|k-1} H_k^T (H_k P_{k|k-1} H_k^T + R)^{-1}$$を算出する過程で、行列の乗算と逆行列計算が発生します。
Madgwickがベクトル演算のみで完結するのに対し、EKFはこれら**行列演算(Matrix Algebra)**を毎周期行うため、計算コストは必然的に高くなります。
2. Round 1:計算負荷の評価(処理時間)
STM32のDWTサイクルカウンタを用いて、1回の更新処理にかかる実行時間をマイクロ秒単位で計測しました。
| アルゴリズム | 実行時間 ($\mu s$) | 負荷率 (10ms周期対比) |
|---|---|---|
| Madgwick | 14.74 | 0.15 % |
| EKF | 237.96 | 2.38 % |
【考察】
Madgwickフィルタの計算効率の良さが際立っており、EKFの約1/16の時間で処理が完了しています。もし演算能力が限られたマイコン(Arduino Uno等)を使用する場合や、数kHzの超高速ループを回す場合は、迷わずMadgwickを選択すべき結果です。
しかし、今回のターゲットであるSTM32G474(170MHz)にとっては、EKFの 238us という負荷は、制御周期(10,000us)のわずか 2.4% に過ぎません。
この結果から、「本システムにおいては、EKFの計算負荷は十分に許容範囲内である」 と判断できます。処理速度を理由にEKFを諦める必要はありません。
3. Round 2:静特性の評価(ノイズ耐性)
倒立振子の制御において、角度データのノイズはD制御(微分項)によって増幅され、モータの振動や発熱(ジジジジ…という音)の直接的な原因となります。
センサを机に固定し、静止させた状態での出力波形を比較します。
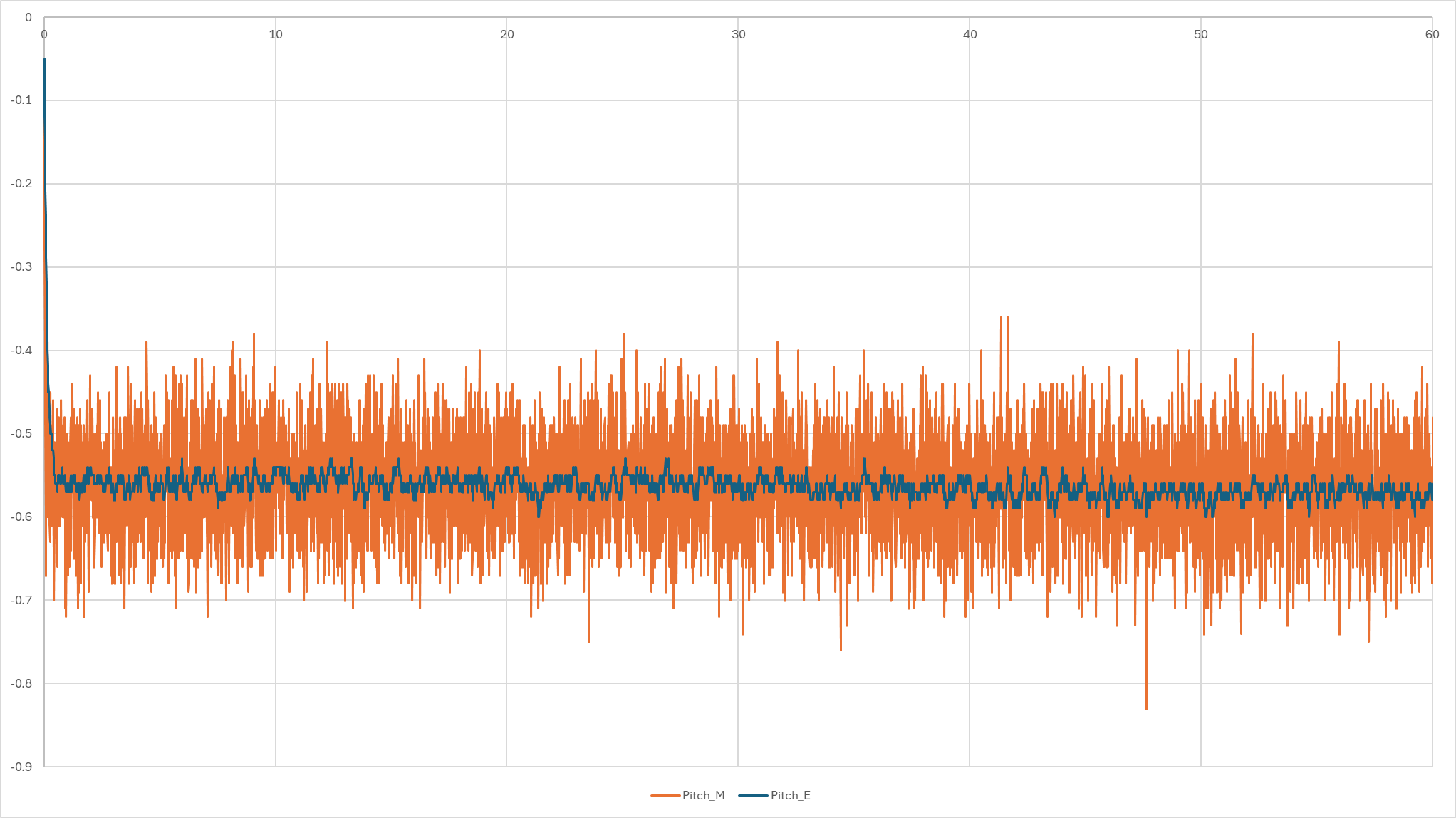
(凡例:橙=Madgwick, 青=EKF)
【考察】
- Madgwick (橙): 常に $\pm 0.1 \sim 0.2^\circ$ 程度の振幅で微振動しています。ゲイン($\beta$)を下げることで滑らかにすることは可能ですが、後述する応答性が悪化するというトレードオフがあります。
- EKF (青): 圧倒的な静粛性を示しており、変動幅は $\pm 0.02^\circ$ 以下に抑えられています。
EKFは「観測ノイズ共分散 $R$ 」をパラメータとして持っており、「センサが静止している(=観測値が信頼できる範囲内である)」という情報を数式的に処理できるため、この高い安定性が実現できています。
4. Round 3:動特性の評価(応答性・追従性)
静特性に加え、実際の制御で重要となる動的な応答性を確認します。
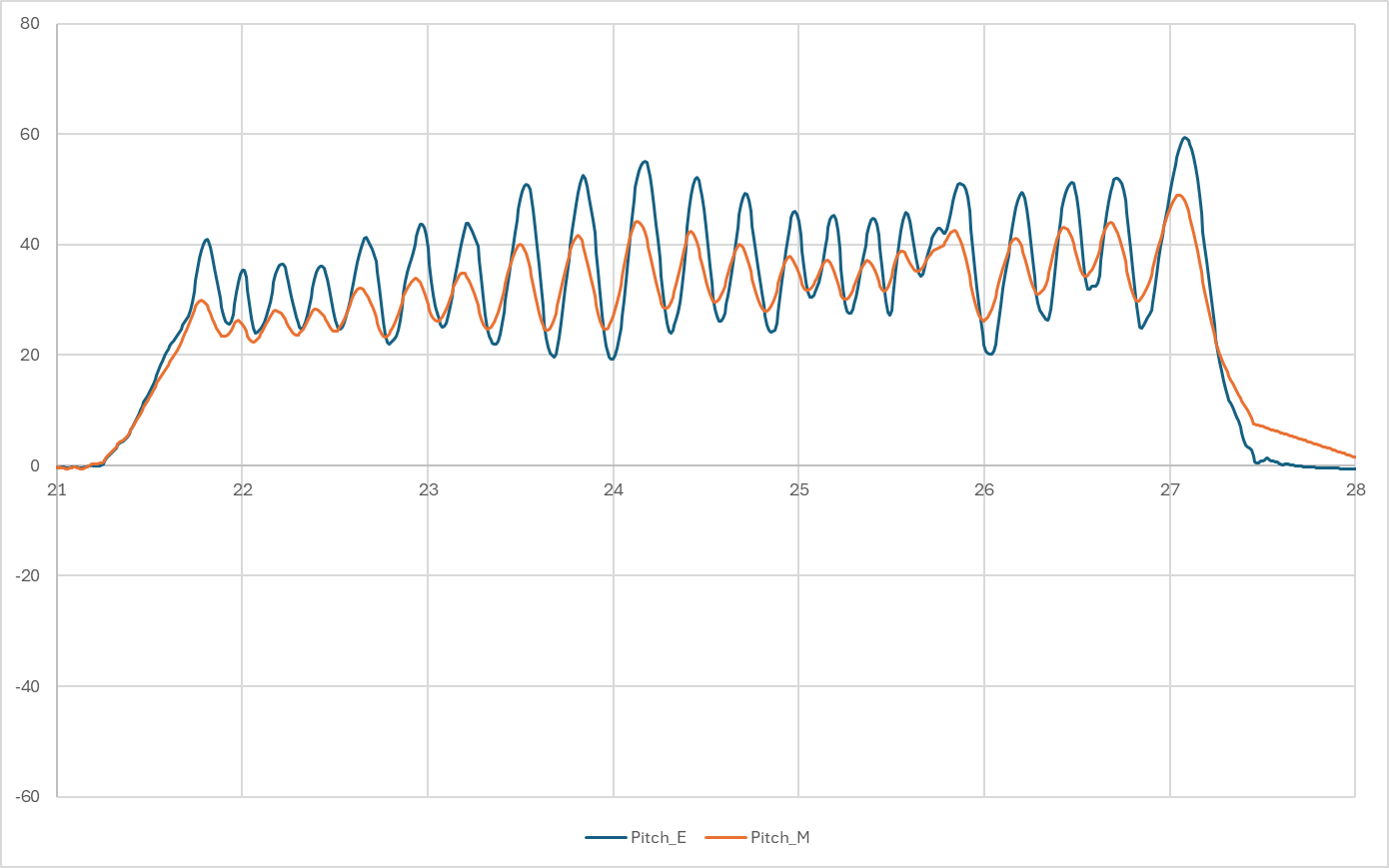
センサを手で持ち、 $\pm 40^\circ \sim 60^\circ$ の範囲で 「前半:ゆっくりとした大きな動き」と「後半:激しい振動」 を与えた際の波形です。
① 低周波領域(~20秒):ゆっくりとした追従
グラフ前半(0秒~20秒)の、比較的緩やかな動きに注目します。
- Madgwick (橙): 概ねEKFと同じ軌道を描いていますが、折り返し地点(頂点)での形状が少し丸まっており、実際の角度よりもわずかに小さく出力される傾向があります。
- EKF (青): 加速度の変化に対して鋭敏に反応し、頂点付近でも波形が鈍ることなく、物理的な動きを忠実にトレースしています。
② 高周波領域(21秒~):激しい振動への耐性
グラフ後半(21秒以降)、手首を使って激しくシェイクした場面で、両者の性能差が決定的となりました。詳細を確認するため、この部分を拡大します。
【詳細考察】
- 振幅の減衰(ゲイン低下)
- Madgwick (橙): 激しい振動に対してフィルタが強くかかりすぎ、波形の振幅が著しく減衰しています。EKFが示している $\pm 50 \sim 60^\circ$ の動きに対し、Madgwickは $\pm 30 \sim 40^\circ$ 程度しか出力できていません。これは 「実際の傾きよりも小さく見積もってしまう」 ことを意味し、倒立制御におけるトルク不足(転倒)の原因となります。
- EKF (青): 高周波な入力に対してもゲインが低下せず、鋭いピーク値を正確に捉え続けています。
- 位相遅れ(Phase Lag)
-
EKFの遅延: 波形の「山」のタイミングを比較すると、EKF(青)はMadgwickに対してわずかに遅れていることが見て取れます。これは、EKFの複雑な行列演算処理や、ノイズ除去のためのフィルタリング効果による物理的なタイムラグです。
-
判定: しかし、この微小な遅れ(数ミリ秒程度)よりも、Madgwickにおける「振幅の大幅な減衰」の方が制御にとっては致命的です。多少の遅れがあっても、「今、何度傾いているか」という情報を正確に伝えられるEKFの方が、姿勢制御においては信頼性が高いと言えます。
5. 総合考察:なぜ差が出たのか?
Madgwickフィルタも本来は非常に優秀なアルゴリズムですが、今回の比較でEKFに分があった理由として、以下の2点が考えられます。
-
地磁気センサの不在:
Madgwickフィルタ(特にAHRS版)は、地磁気ベクトルを使ってヨー軸のドリフト補正を行う際に真価を発揮します。今回は6軸(IMU版)での実装だったため、Madgwickの強みが完全には活かせなかった可能性があります。 -
パラメータ調整の自由度:
Madgwickは基本的にゲイン の一つで調整を行いますが、EKFは「プロセスの信頼度 」と「観測の信頼度 」を個別に設定できます。これにより、「静止時は加速度を信じてガチガチに固める」「動くときはジャイロを信じて追従する」といった柔軟な切り替えが、数式レベルで自動的に行われています。
6. 結論:用途に応じた使い分け
今回の検証により、我々は2つの強力な「武器」の特性を理解しました。
-
処理能力に余裕がない場合 → Madgwickフィルタ
計算が圧倒的に軽く、実用十分な精度が出る。8bit/16bitマイコンを使用する場合や、リソースがカツカツな場合には最適解となる。 -
処理能力に余裕があり、質を求める場合 → EKF
計算は重いが、ノイズ除去と応答性のバランスが極めて高い。STM32G4のようなFPU搭載マイコンを使うなら、こちらを採用するメリットが大きい。
【本プロジェクトでの選定】
今回はSTM32G474の演算能力に十分な余力があるため、制御の安定性と高周波領域での追従性を最優先し、「拡張カルマンフィルタ(EKF)」を採用することとします。
この高精度な角度データを用いれば、繊細なトルク制御が必要なCubliの姿勢制御もスムーズに行えるはずです。
次のアクション
最強の「目(姿勢推定)」は完成しました。
次回(Day 22)は、このフィルタのパラメータ調整を効率化するために、STM32のUSB機能を活用した 「USB CDC(仮想COMポート)」 の実装を行います。
UART-USB変換器を使わず、USBケーブル1本でPCと爆速通信を行い、内部状態をリアルタイムに可視化できる環境を構築します。お楽しみに!
アドベントカレンダー参加中
STM32×AIで「3軸倒立振子」を作る25日間(ひとりアドカレ)Advent Calendar 2025