「風の噂で、20数人いれば、50%の確率で同じ誕生日のペアが存在する」とかなんとか、、、というのを聞いたので実際に計算してみました
import matplotlib.pyplot as plt
import numpy as np
print("Find the probability of existing person of same birth day in a group")
print("n: the number of people in a group")
x = np.linspace(2, 366, 364)
y = []
no_match = 1
for n in range(2, 366):
no_match *= (366-n) / 365
match = 1 - no_match
y.append(match)
print("n = %3d: %f" % (n, match))
plt.plot(x, y)
plt.show()
このプログラムを動かすと
Find the probability of existing person of same birth day in a group
n: the number of people in a group
n = 2: 0.002740
n = 3: 0.008204
n = 4: 0.016356
n = 5: 0.027136
n = 6: 0.040462
n = 7: 0.056236
n = 8: 0.074335
n = 9: 0.094624
n = 10: 0.116948
n = 11: 0.141141
n = 12: 0.167025
n = 13: 0.194410
n = 14: 0.223103
n = 15: 0.252901
n = 16: 0.283604
n = 17: 0.315008
n = 18: 0.346911
n = 19: 0.379119
n = 20: 0.411438
n = 21: 0.443688
n = 22: 0.475695
n = 23: 0.507297
n = 24: 0.538344
n = 25: 0.568700
n = 26: 0.598241
n = 27: 0.626859
n = 28: 0.654461
n = 29: 0.680969
n = 30: 0.706316
n = 31: 0.730455
n = 32: 0.753348
n = 33: 0.774972
n = 34: 0.795317
n = 35: 0.814383
n = 36: 0.832182
n = 37: 0.848734
n = 38: 0.864068
n = 39: 0.878220
n = 40: 0.891232
n = 41: 0.903152
n = 42: 0.914030
n = 43: 0.923923
n = 44: 0.932885
n = 45: 0.940976
n = 46: 0.948253
n = 47: 0.954774
n = 48: 0.960598
n = 49: 0.965780
n = 50: 0.970374
n = 51: 0.974432
n = 52: 0.978005
n = 53: 0.981138
n = 54: 0.983877
n = 55: 0.986262
n = 56: 0.988332
n = 57: 0.990122
n = 58: 0.991665
n = 59: 0.992989
n = 60: 0.994123
n = 61: 0.995089
n = 62: 0.995910
n = 63: 0.996604
n = 64: 0.997190
n = 65: 0.997683
n = 66: 0.998096
n = 67: 0.998440
n = 68: 0.998726
n = 69: 0.998964
n = 70: 0.999160
n = 71: 0.999321
n = 72: 0.999453
n = 73: 0.999561
n = 74: 0.999649
n = 75: 0.999720
n = 76: 0.999777
n = 77: 0.999824
n = 78: 0.999861
n = 79: 0.999891
n = 80: 0.999914
.
.
.
.
.
というようにコンソールに出力されて
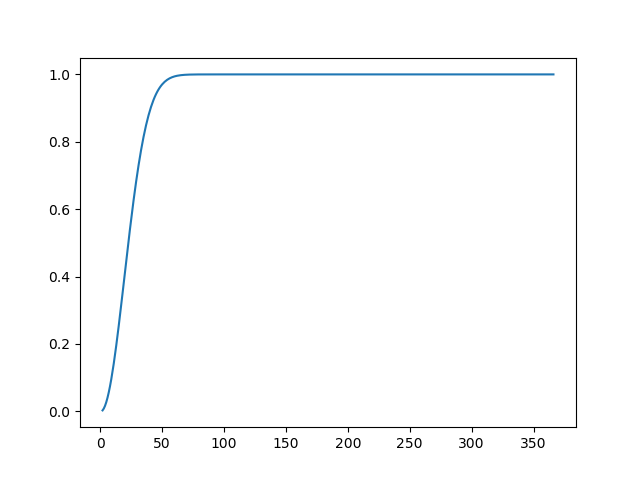
このような画像が画面に出力されます。
確かにこれを見ると、23人のところで、確率が50%を超えますね。
50人もいればほぼ100%ペアが存在する。
さて、ちょっとプログラムを解説
ざっくりやっていることというのは
・全員が違う誕生日である確率を求める
・余事象を求める
だけです
まず
x = np.linspace(2, 366, 364)
y = []
これは
「xを2から366までを364分割する」
という命令です
no_match = 1
for n in range(2, 366):
no_match *= (366-n) / 365
match = 1 - no_match
y.append(match)
print("n = %3d: %f" % (n, match))
ここではまずno_matchを1で初期化しておきます
そしてnを2~365まで回します
2人以上じゃないと、当たる確率は0だし
366人以上だと必ず1組は存在するので(うるう年は考えない)
この範囲です。
2人目が、1人目と違う誕生日である確率は
364/365
3人目が、1人目と2人目とも違う誕生日である確率は
363/365
なので、3人とも誕生日が違う確率は
1 - (364/365) * (363/365)なので
以下ループ
.
.
.
と続いていくので、その都度計算して
yに追記してコンソールに出力していくという形を取っています。
ループが終わると、xとyのデータが完成しているので
それをmatplotlibのx、yに突っ込んでグラフを出力すれば完成です