0. はじめに
2020年9月7日にAtCoder公式のアルゴリズム集 AtCoder Library (ACL)が公開されました。
私はACLに収録されているアルゴリズムのほとんどが初見だったのでいい機会だと思い、アルゴリズムの勉強からPythonでの実装までを行いました。
この記事ではmathをみていきます。
mathは数論的アルゴリズムの詰め合わせで内容は以下の通りです。
| 名称 | 概要 |
|---|---|
| pow_mod | $x^n \pmod{m}$ の計算。 |
| inv_mod | $m$ を法とした $x$ の逆元 $y$ の計算。 |
| crt | 長さ $n$ の数列{$r_i$}, {$m_i$}に対して連立合同式 $x \equiv r_i \pmod{m_i} $$(0 \leq i < n)$ の解の計算。 |
| floor_sum | 自然数 $m$ 、整数 $a, b$、 0以上の整数 $n$ に対して $\sum_{i=0}^{n-1}{\left\lfloor\frac{ai+b}{m}\right\rfloor}$ の計算。 |
対象としている読者
- 中国剰余定理ってなに?という方。
- floor_sumってなに?という方。
- ACLのコードを見てみたけど何をしているのかわからない方。
- C++はわからないのでPythonで読み進めたい方。
参考にしたもの
@drkenさんによる中国剰余定理の解説記事です。応用例や問題例まで書かれています。
@kyopuro_friendsさんのfloor_sumに関するツイートです。
1. pow_mod
x^n \pmod{m}
を繰り返し二乗法を用いて計算します。
internal_mathのpow_modとの違いは、あまりを取るときに算術演算子"%"でなくBarrett reductionを用いていることです。
繰り返し二乗法およびBarrett reductionの詳細は internal_math編①にありますのでそちらをご覧ください。
Pythonでの実装は以下の通りです。ACLにおいてsafe_modを用いている部分はPythonにおいて同等の機能である算術演算子"%"で代用しています。また、Barrett reductionはBarrettとしてすでに実装されているものとします。
from internal_math import Barrett
def pow_mod(x, n, m):
assert n >= 0 and m >= 1
if m == 1: return 0
bt = Barrett(m)
r, y = 1, x % m
while n:
if n & 1: r = bt.mul(r, y)
y = bt.mul(y, y)
n >>= 1
return r
print(pow_mod(3, 4, 5)) # 1
print(pow_mod(13, 1000000000, 1000000007)) # 94858115
なお、Pythonでは組み込み関数pow( )がpow_modに相当するのでこの実装は不要です。
Barrett reductionによる高速化も関数(メソッド)呼び出しのオーバーヘッドによる低速化を上回るものではないと思います。(競技プログラミングでは扱わないような巨大な数になれば変わるかもしれません。)
print(pow(3, 4, 5)) # 1
print(pow(13, 1000000000, 1000000007)) # 94858115
2. inv_mod
$m$ を法とし $m$ と互いに素な整数 $x$ の逆元 $y$ を求めます。
すなわち
xy \equiv 1 \pmod{m}
を満たす $y$ を求めます。この合同式は整数 $z$ を用いて
xy + mz = 1
と書くことができるので、この一次不定方程式を解くことになります。
そしてこの解は拡張ユークリッドの互除法によって求めることができます。拡張ユークリッドの互除法はinternal_mathで"inv_gcd"として実装されていますので詳細については internal_math編①をご覧ください。
ではinv_modを実装します。inv_gcdはすでに実装しているとします。
from internal_math import inv_gcd
def inv_mod(x, m):
assert 1 <= m
z = inv_gcd(x, m)
assert z[0] == 1
return z[1]
print(inv_mod(2, 3)) # 2
print(inv_mod(2, 13)) # 7
ちなみに...
Pythonの組み込み関数pow()でも逆元を求めることができます。
print(pow(2, -1, 3)) # 2
print(pow(2, -1, 13)) # 7
こちらも拡張ユークリッドの互除法を用いた実装がされていますのでinv_modは実装しなくても良いです。
ただし、inv_gcdは他でも使うので必要です。
注意 この機能はPython3.8で追加されたものです。PyPy3(7.3.0)では使えません。
3. crt
長さ $n$ の自然数列 ${m_i}$ と整数列$ {r_i}$ に対し 連立合同式
x \equiv r_i \pmod{m_i} \;\;(\forall i \in \{0, 1, \cdots , n-1\})
を考えます。
最初に簡単な例題を見て、次に連立合同式が解を持つ条件と解が一意であることを示します。
その後、実際に解を求める方法を見ていきます。
3.1. 簡単な例題
具体例として $r={3, 4}, m = {5, 7}$ の場合を考えます。すなわち
\left\{
\begin{aligned}
x \equiv 3 \pmod{5}\\
x \equiv 4 \pmod{7}
\end{aligned}
\right.
を解くことを考えます。
まず1つ目の式を満たす $x$ を考えます。これは整数 $k$ を用いて $x = 5k + 3$ とかけることがわかります。そして、この $x$ が満たすべき条件として2つ目の式を考えます。
$x$ を2つ目の式に代入すると
\begin{aligned}
5k + 3 &\equiv 4 \pmod{7}\\
5k &\equiv 1 \pmod{7}\\
k &\equiv 3 \pmod{7}
\end{aligned}
となります。最後の行へは $7$ を法とした $5$ の逆元($=3$)を両辺にかけています。
$k$ は整数 $l$ を用いて $k = 7l + 3$ とかけることがわかったので $x = 5(7l + 3) + 3$ が得られます。
以上より連立合同式の解は
x \equiv 18 \pmod{35}
です。
3.2. 解の存在条件(n=2の場合)
それでは連立合同式が解を持つ条件を見ていきます。まず $n=2$ の場合です。
連立合同式
\left\{
\begin{aligned}
x \equiv r_0 \pmod{m_0}\\
x \equiv r_1 \pmod{m_1}
\end{aligned}
\right.
が ${\rm lcm}(m_0, m_1)$ を法として解を持つ
$\Leftrightarrow r_0 \equiv r_1 \pmod{\gcd(m_0, m_1)}$
(証明)
$\Rightarrow$ :
$x$ が連立合同式の解であるとき、$x \equiv r_0 \pmod{\gcd(m_0, m_1)}$ かつ $x \equiv r_1 \pmod{\gcd(m_0, m_1)}$ であることは明らかなので $r_0 \equiv r_1 \pmod{\gcd(m_0, m_1)}$ を満たす。
$\Leftarrow$ :
1つ目の式から $x$ は整数 $k$ を用いて $x = m_0k + r_0$ とかけることがわかる。
これを2つ目の式に代入し
\begin{aligned}
m_0k + r_0 &\equiv r_1 &\pmod{m_1}\\
m_0k &\equiv r_1 - r_0 &\pmod{m_1}\\
\gcd(m_0, m_1) k &\equiv (r_1 - r_0) m_{0(1)}^{-1} &\pmod{m_1}
\end{aligned}
となる。ここで $m_{0(1)}^{-1}$ は
m_0 m_{0(1)}^{-1} \equiv \gcd(m_0, m_1) \pmod{m_1}
を満たす。
いま、$r_0 \equiv r_1 \pmod{\gcd(m_0, m_1)}$ が満たされていると仮定しているので $r_1 - r_0$ は ${\gcd(m_0, m_1)}$ の倍数である。よって
k \equiv \frac{r_1 - r_0}{\gcd(m_0, m_1)}m_{0(1)}^{-1} \pmod{\frac{m_1}{\gcd(m_0, m_1)}}
となる。すなわち、$k$ は整数 $l$ を用いて
k = l \frac{m_1}{\gcd(m_0, m_1)} + \frac{r_1 - r_0}{\gcd(m_0, m_1)}m_{0(1)}^{-1}
と表せる。したがって $x$ は
\begin{aligned}
x &= m_0(l \frac{m_1}{\gcd(m_0, m_1)} + \frac{r_1 - r_0}{\gcd(m_0, m_1)}m_{0(1)}^{-1}) + r_0\\[3ex]
&= l \frac{m_0m_1}{\gcd(m_0, m_1)} + r_0 + \frac{r_1 - r_0}{\gcd(m_0, m_1)}m_0m_{0(1)}^{-1}
\end{aligned}
である。これを ${\rm lcm}(m_0, m_1)$ を法とした合同式で書けば
x \equiv r_0 + \frac{r_1 - r_0}{\gcd(m_0, m_1)}m_0m_{0(1)}^{-1} \pmod{{\rm lcm}(m_0, m_1)}
となり、${\rm lcm}(m_0, m_1)$ を法とした解が存在することが示された。
(証明終)
3.3. 解の存在条件(nが3以上の場合)
続いて $n\geq 3$ の場合を見ていきます。
連立合同式
\left\{
\begin{aligned}
x &\equiv r_0 &\pmod{m_0}\\
x &\equiv r_1 &\pmod{m_1}\\
&\cdots\\
x &\equiv r_{n-1} &\pmod{m_{n-1}}
\end{aligned}
\right.
が ${\rm lcm}(m_0, m_1, \cdots , m_{n-1})$ を法として解を持つ
$\Leftrightarrow r_i \equiv r_j \pmod{\gcd(m_i, m_j)} ;,;;i, j \in {0, 1, \cdots, n-1}$
(証明)
$\Rightarrow$ :
$n=2$ の場合と同様で明らかである。
$\Leftarrow$ :
$n=3$ の場合を考える。いま、$r_0 \equiv r_1 \pmod{\gcd(m_0, m_1)}$ なので前節より連立合同式
\left\{
\begin{aligned}
x \equiv r_0 \pmod{m_0}\\
x \equiv r_1 \pmod{m_1}
\end{aligned}
\right.
の解が ${\rm lcm}(m_0, m_1)$ を法として存在し、この解を
x \equiv x_2 \pmod{{\rm lcm}(m_0, m_1)}
とおく。すると $x_2 \equiv r_0 \pmod{m_0}$ なので
\begin{aligned}
x_2 - r_2 &\equiv r_0 - r_2 \pmod{m_0}\\
&\equiv r_0 - r_2 \pmod{\gcd(m_0, m_2)}\\
&\equiv 0 \pmod{\gcd(m_0, m_2)}
\end{aligned}
より
x_2 \equiv r_2 \pmod{\gcd(m_0, m_2)}
となる。同様に
x_2 \equiv r_2 \pmod{\gcd(m_1, m_2)}
である。よって
x_2 \equiv r_2 \pmod{{\rm lcm}(\gcd(m_0, m_2), \gcd(m_1, m_2))}
ここで、
{\rm lcm}(\gcd(a, c), \gcd(b, c)) = \gcd({\rm lcm}(a, b), c)
を用いると
x_2 \equiv r_2 \pmod{\gcd({\rm lcm}(m_0, m_1), m_2)}
となる。したがって、前節より連立合同式
\left\{
\begin{aligned}
x &\equiv x_2 \pmod{{\rm lcm}(m_0, m_1)}\\
x &\equiv r_2 \pmod{m_2}
\end{aligned}
\right.
は ${\rm lcm}({\rm lcm}(m_0, m_1), m_2)$ を法とした解を持つ.この $x_2$ は
\left\{
\begin{aligned}
x \equiv r_0 \pmod{m_0}\\
x \equiv r_1 \pmod{m_1}
\end{aligned}
\right.
の解であり、また ${\rm lcm}({\rm lcm}(m_0, m_1), m_2) = {\rm lcm}(m_0, m_1, m_2)$ なので連立合同式
\left\{
\begin{aligned}
x \equiv r_0 \pmod{m_0}\\
x \equiv r_1 \pmod{m_1}\\
x \equiv r_2 \pmod{m_2}
\end{aligned}
\right.
は ${\rm lcm}(m_0, m_1, m_2)$ を法とした解を持つ。
以降、帰納的に $n \geq 3$ に対して連立合同式
\left\{
\begin{aligned}
x &\equiv r_0 &\pmod{m_0}\\
x &\equiv r_1 &\pmod{m_1}\\
&\cdots\\
x &\equiv r_{n-1} &\pmod{m_{n-1}}
\end{aligned}
\right.
が ${\rm lcm}(m_0, m_1, \cdots , m_{n-1})$ を法として解を持つことを示せる。
(証明終)
3.4. 解の一意性
連立合同式
\left\{
\begin{aligned}
x &\equiv r_0 &\pmod{m_0}\\
x &\equiv r_1 &\pmod{m_1}\\
&\cdots\\
x &\equiv r_{n-1} &\pmod{m_{n-1}}
\end{aligned}
\right.
の解が ${\rm lcm}(m_0, m_1, \cdots , m_{n-1})$ を法として一意であることを背理法で示します。
(証明)
いま、${\rm lcm}(m_0, m_1, \cdots , m_{n-1})$ を法とした解が2つ存在すると仮定しこれを
x \equiv y \;\;,\;\; x \equiv z \pmod{{\rm lcm}(m_0, m_1, \cdots , m_{n-1})}
とする。すなわち、この $y, z$ は
y \not\equiv z \pmod{{\rm lcm}(m_0, m_1, \cdots , m_{n-1})}
を満たす。
いま $i = 0, 1, \cdots, n-1$ について
y \equiv r_i \pmod{m_i}\;\; かつ\;\;z \equiv r_i \pmod{m_i}
なので
y \equiv z \pmod{m_i}
である。よって
y \equiv z \pmod{{\rm lcm}(m_0, m_1, \cdots , m_{n-1})}
であり、これは仮定と矛盾する。
したがって、${\rm lcm}(m_0, m_1, \cdots , m_{n-1})$ を法とした解は一意である。
(証明終)
3.5. 中国剰余定理
ここまで $m_i$ は正整数という条件しかありませんでしたが、この節では任意の $i, j$ について $m_i$ と $m_j$ が互いに素の場合を考えてみます。
このとき、
\begin{aligned}
\gcd(m_i, m_j) &= 1\\
{\rm lcm}(m_0, m_1, \cdots, m_{n-1}) &= m_0m_1\cdots m_{n-1}
\end{aligned}
なので連立合同式
\left\{
\begin{aligned}
x &\equiv r_0 &\pmod{m_0}\\
x &\equiv r_1 &\pmod{m_1}\\
&\cdots\\
x &\equiv r_{n-1} &\pmod{m_{n-1}}
\end{aligned}
\right.
は常に $m_0m_1\cdots m_{n-1}$ を法とした解を持ちます。
これを中国剰余定理(Chinese Remainder Theorem, CRT)と言います。
3.6. 解を求める方法
解の存在条件の証明で示したように連立合同式
\left\{
\begin{aligned}
x \equiv r_0 \pmod{m_0}\\
x \equiv r_1 \pmod{m_1}
\end{aligned}
\right.
の解は(存在するならば)
x \equiv r_0 + \frac{r_1 - r_0}{\gcd(m_0, m_1)}m_0m_{0(1)}^{-1} \pmod{{\rm lcm}(m_0, m_1)}
と書けます。
これを少し見方を変えて次のように見ます。
-
いま、$x \equiv r_0 \pmod{m_0}$ は合同式
x \equiv r_0 \pmod{m_0}の解である。
-
これを
\begin{aligned} r_0 &\leftarrow r_0 + \frac{r_1 - r_0}{\gcd(m_0, m_1)}m_0m_{0(1)}^{-1}\\[3ex] m_0 &\leftarrow {\rm lcm}(m_0, m_1) \end{aligned}とすることで連立合同式
\left\{ \begin{aligned} x \equiv r_0 \pmod{m_0}\\ x \equiv r_1 \pmod{m_1} \end{aligned} \right.の解となる。
このように見ると、1番目の合同式の値 $r_0, m_0$ を初期値として、2番目以降の合同式の値 $r_i, m_i$ を使って $r_0, m_0$ を遷移させていくことで最終的に $r_0, m_0$ は $n$ 個の合同式を満たす解になることがわかります。
さらに、1番目の合同式だけ初期値として特別扱いするのも統一性に欠けるので初期値を $r_0 = 0, m_0 = 1$ に固定し、1番目の合同式の値も $r_0, m_0$ を遷移させる為に使うことにします。これは0番目の合同式として $x \equiv 0 \pmod{1}$ というものを追加することと等しいです。この合同式は任意の整数について満たされるので追加しても問題ありません。
3.7. 実装
それではcrt()を実装します。この関数は長さ $n$ の自然数列 ${m_i}$ と整数列$ {r_i}$ の入力に対し連立合同式
\left\{
\begin{aligned}
x &\equiv r_0 &\pmod{m_0}\\
x &\equiv r_1 &\pmod{m_1}\\
&\cdots\\
x &\equiv r_{n-1} &\pmod{m_{n-1}}
\end{aligned}
\right.
の解が存在すればその解を $x \equiv y \pmod{z := {\rm lcm}(m_0, m_1, \cdots, m_{n-1})}$ とし(y, z)を返します。解が存在しなければ (0, 0)を返します。$n=0$ の場合は(0, 1)を返します。
なお、拡張ユークリッドの互除法はすでにinternal_mathのなかでinv_gcdとして実装されているものとします。
from internal_math import inv_gcd
def crt(r, m):
assert len(r) == len(m)
n = len(r)
r0, m0 = 0, 1 # 初期値 x = 0 (mod 1)
for i in range(n):
assert m[i] >= 1
#r1, m1は遷移に使う値
r1, m1 = r[i] % m[i], m[i]
#m0がm1以上になるようにする。
if m0 < m1:
r0, r1 = r1, r0
m0, m1 = m1, m0
# m0がm1の倍数のとき gcdはm1、lcmはm0
# 解が存在すれば何も変わらないので以降の手順はスキップ
if m0 % m1 == 0:
if r0 % m1 != r1: return 0, 0
continue
# 拡張ユークリッドの互除法によりgcd(m0, m1)と m0 * im = gcd (mod m1) を満たす imを求める
g, im = inv_gcd(m0, m1)
# 解の存在条件の確認
if (r1 - r0) % g: return 0, 0
"""
r0, m0の遷移
コメントアウト部分はACLでの実装
C++なのでlong longを超えないようにしている
C++ はlcm(m0, m1)で割った余りが負になり得る
"""
# u1 = m1 // g
# x = (r1 - r0) // g % u1 * im % u1
# r0 += x * m0
# m0 *= u1
u1 = m0 * m1 // g
r0 += (r1 - r0) // g * m0 * im % u1
m0 = u1
#if r0 < 0: r0 += m0
return r0, m0
r = [3, 4]
m = [5, 7]
print(crt(r, m)) # [18, 35]
4. floor_sum
0以上の整数 $n$、整数 $a, b$ および1以上の整数 $m$ について
\sum_{i=0}^{n-1}{\left\lfloor \frac{a\cdot i + b}{m}\right\rfloor}
を計算します。
4.1. internal_math の floor_sum_unsignedについて
floor_sumの入力において $a, b$ が0以上の整数に限った場合については、internal_math にfloor_sum_unsignedという名前で実装されています。
本記事ではまず、 $a, b\geq 0$ として話を進め、floor_sum_unsigned を実装しその後、 $a, b$ が負の場合を考えてmath内のfloor_sumを実装します。
4.2. 記号の確認
整数 $x$ と正整数 $y$ について
| 記号 | 説明 |
|---|---|
| $\frac{x}{y}$ | $x$ の $y$ による(通常の)割り算 |
| $\left\lfloor\frac{x}{y}\right\rfloor$ | $x$ の $y$ による割り算の切り捨て(負の無限大への丸め込み) |
| $\left\lceil\frac{x}{y}\right\rceil$ | $x$ の $y$ による割り算の切り上げ(正の無限大への丸め込み) |
| $x % y$ | $x$ を $y$ で割った余り($0 \leq x % y < y$) |
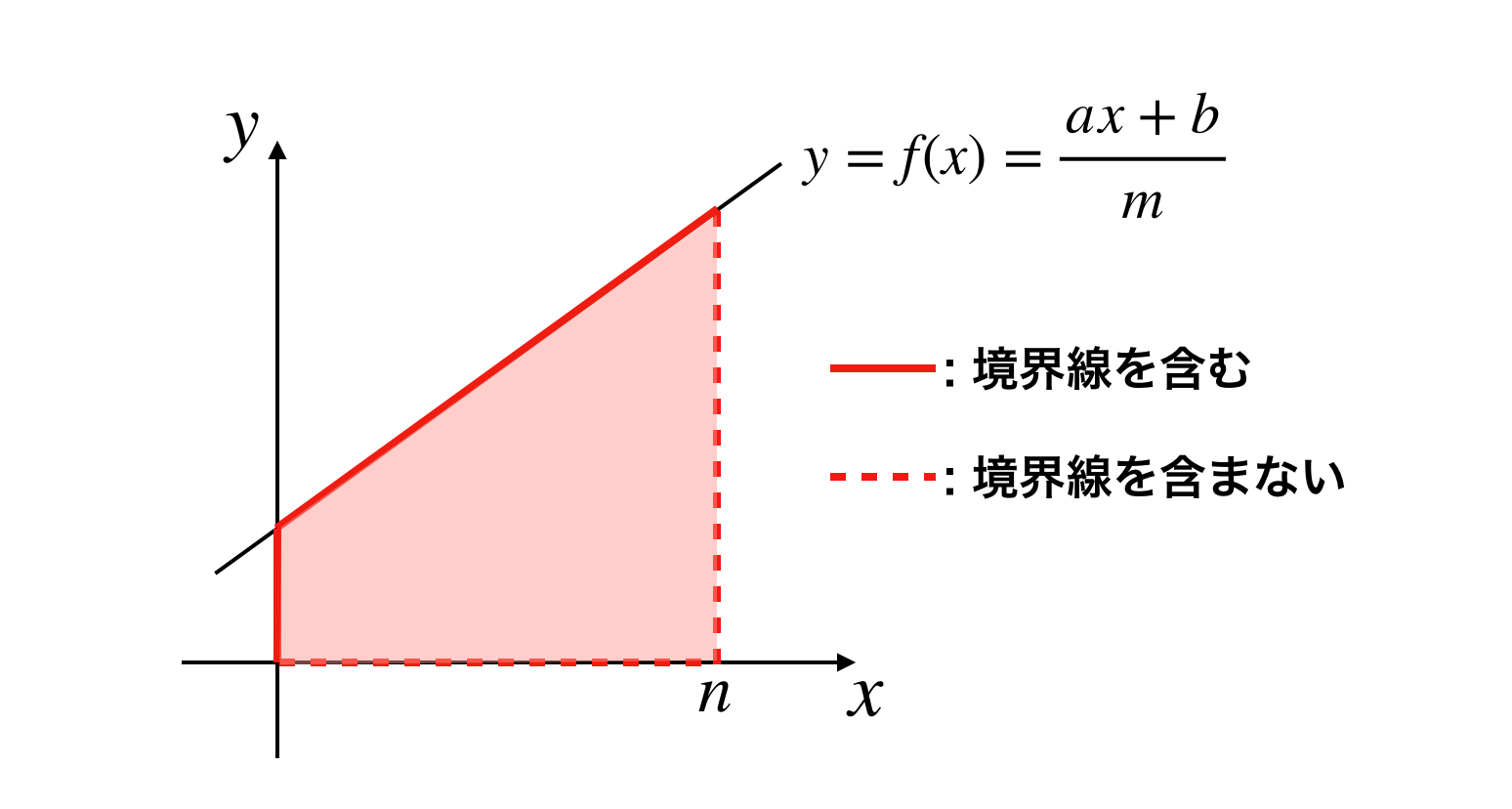
とします。また領域を図示する際、実線は境界線を含むことを、破線は含まないことを示します。
4.3. 問題の把握
ここから、$a, b \geq 0$ とします。
いま
f(i) = \frac{a\cdot i + b}{m}
とおくと
\begin{aligned}
\left\lfloor \frac{a\cdot i + b}{m}\right\rfloor
\Leftrightarrow &\left\lfloor f(i)\right\rfloor\\[2ex]
\Leftrightarrow & (半開区間 (0,f(i)]内の整数の数)
\end{aligned}
となるのでこの問題は結局、下図のような範囲の格子点(x座標、y座標が共に整数の点)の数え上げ問題になります。
4.4. 簡単な部分を探す
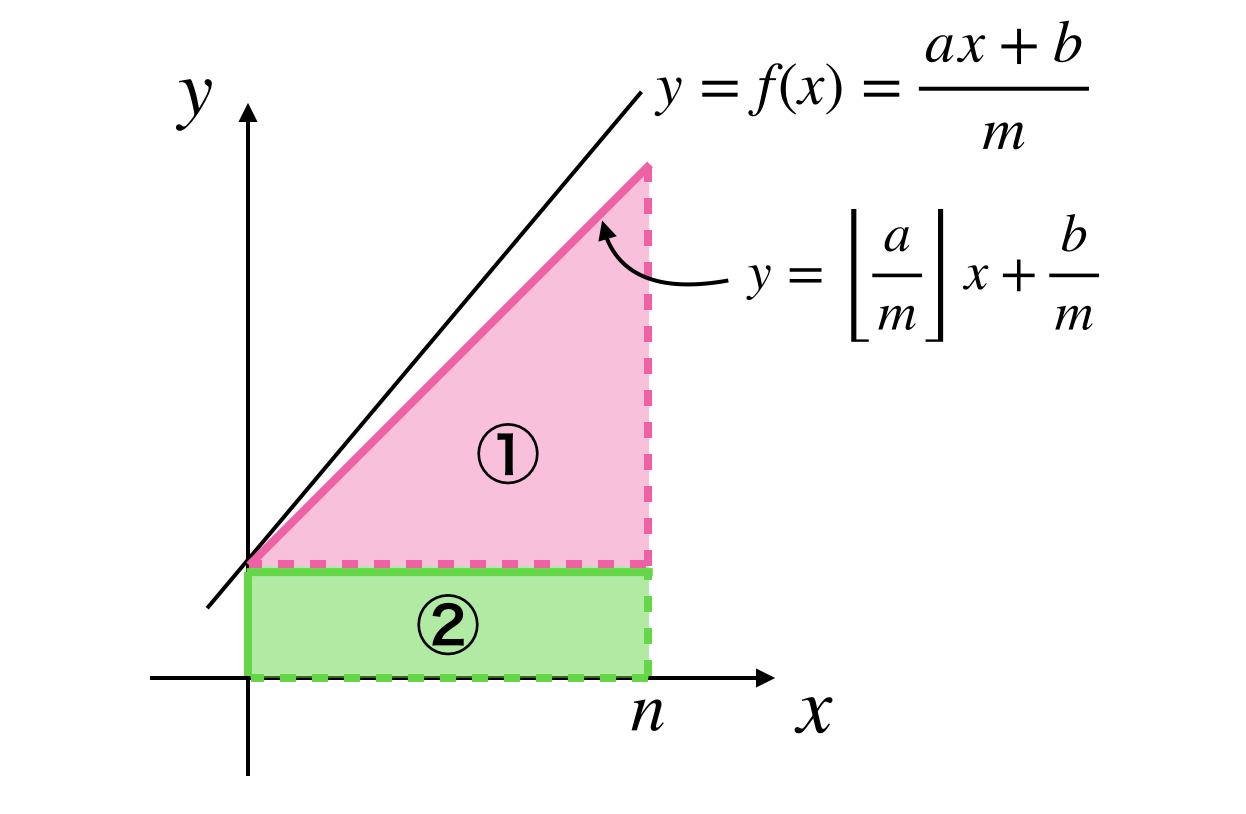
全てを一気に数え上げるのは難しいので、簡単に計算できる部分を探します。
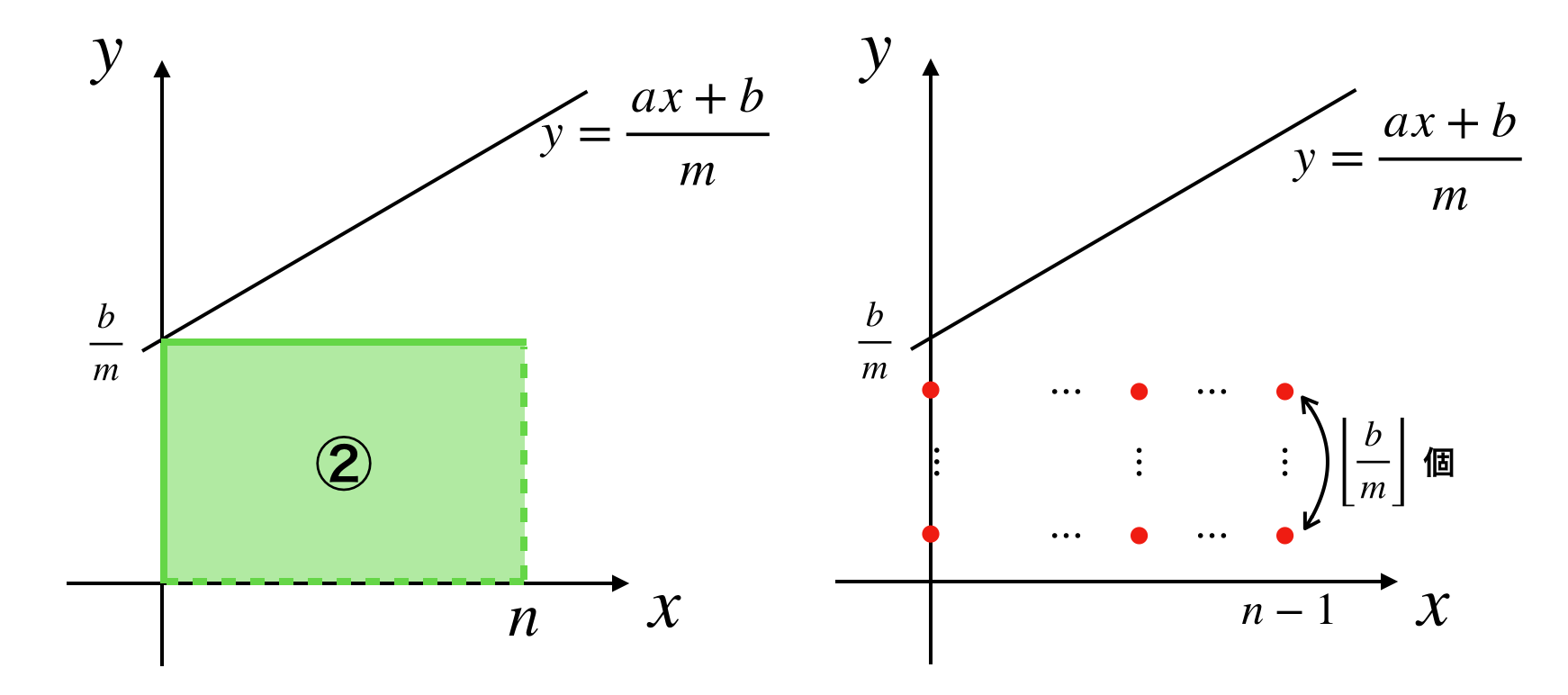
$a \geq m$ の場合には下図の①の領域が、また、$b \geq m$ の場合には②の領域が簡単に計算できます。
よってまずはそれぞれの領域内の格子点の数をみていきます。
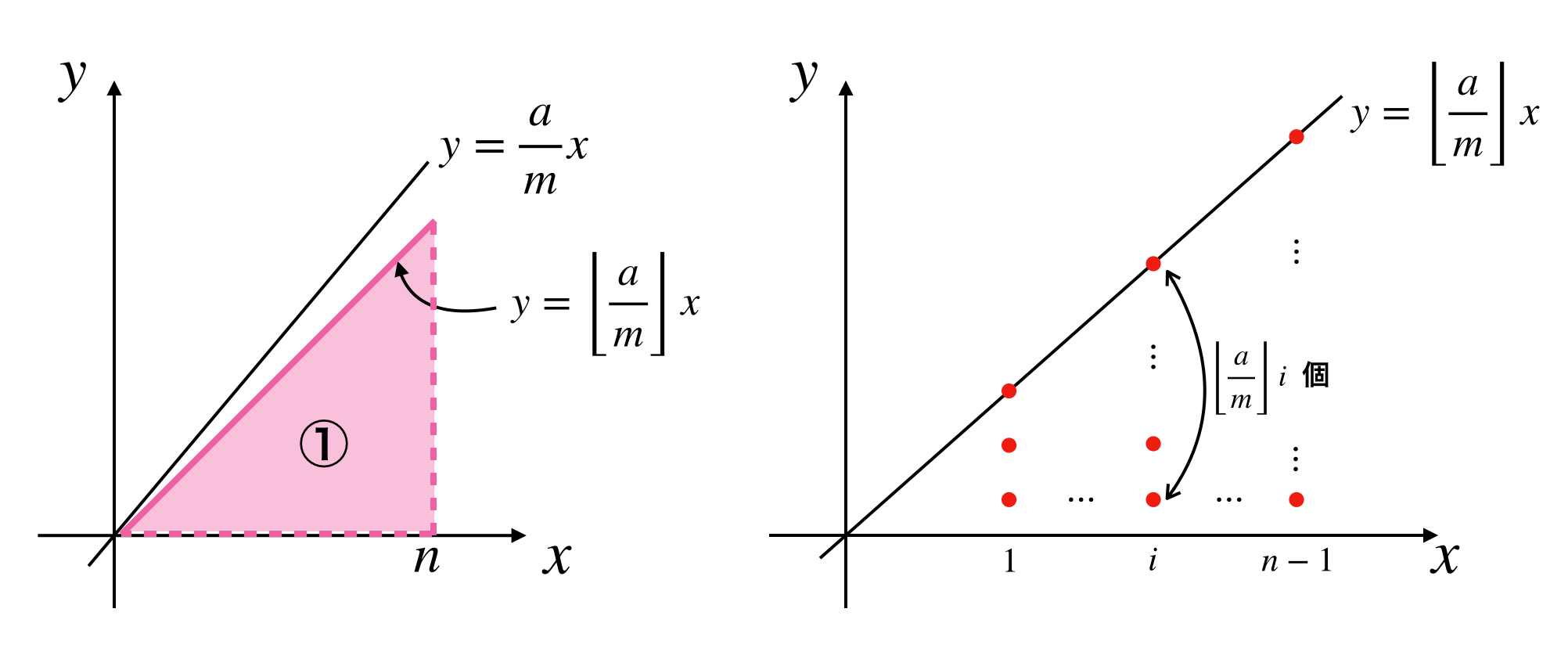
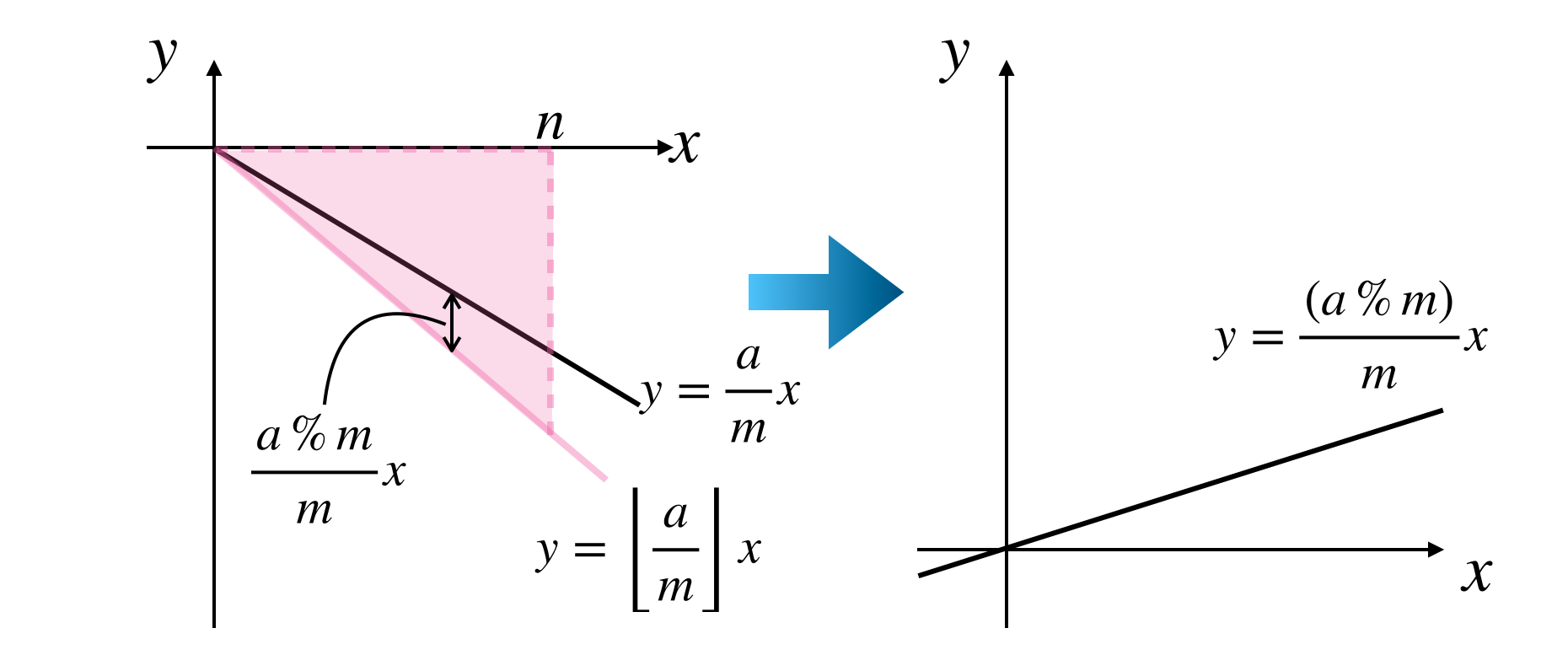
4.5. ①の領域
まず①の領域についてみていきます。ここでは $b$ は関係ないので簡単のため $b=0$ とします。このとき①の領域は下図(左)のようになります。
格子点は上図(右)のようにありますのでこの領域内の格子点の個数は
\begin{aligned}
(領域①の格子点の個数)&= \sum_{i=1}^{n-1}{\left\lfloor\frac{a}{m}\right\rfloor i}\\[3ex]
&= \left\lfloor\frac{a}{m}\right\rfloor \sum_{i=1}^{n-1}{i}\\[3ex]
&= \left\lfloor\frac{a}{m}\right\rfloor \frac{(n-1)n}{2}
\end{aligned}
となります。
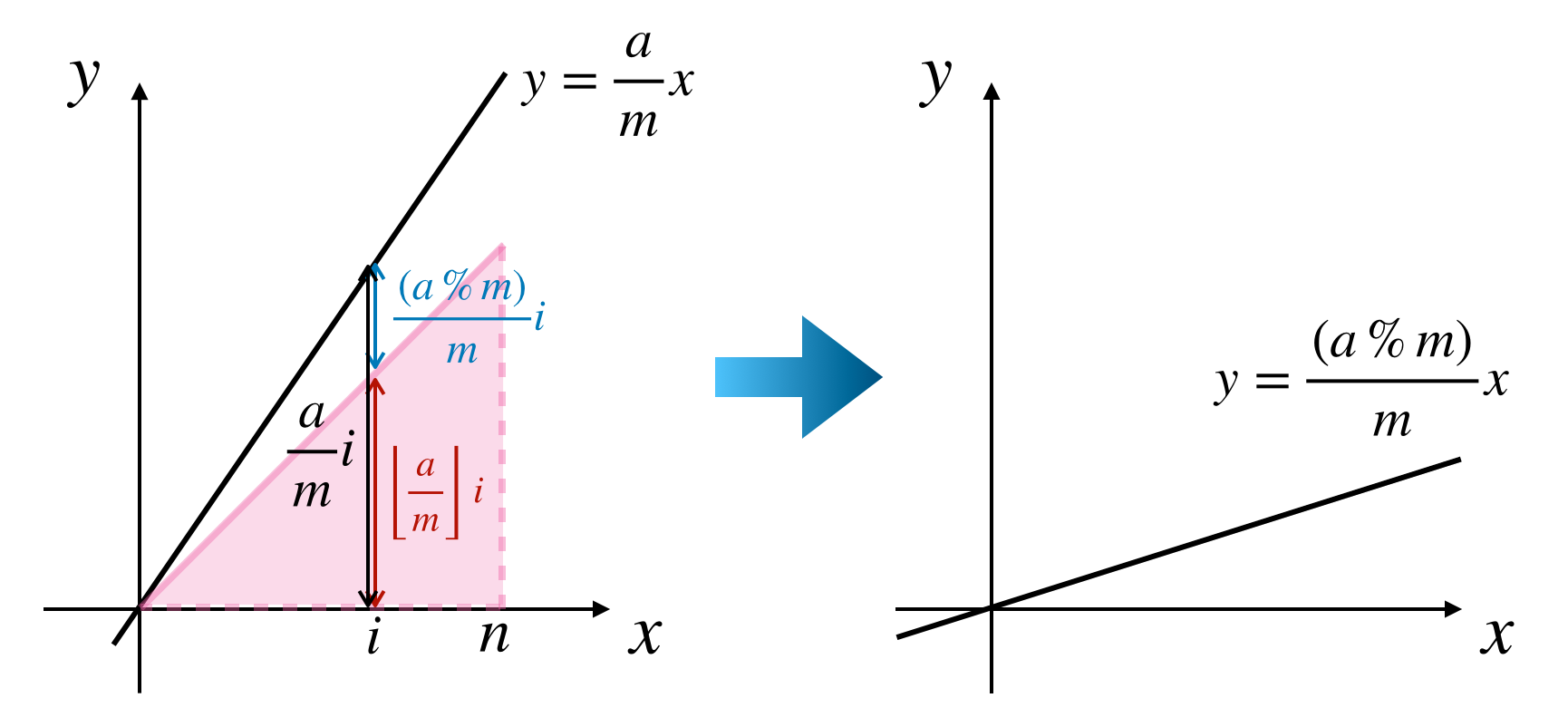
これで①の領域は数えることができたので取り除く必要があります。今数え上げたのは $\frac{a}{m}i$ の内 $\left\lfloor\frac{a}{m}\right\rfloor i$ の部分なので残りは
\begin{aligned}
\frac{a}{m}i - \left\lfloor\frac{a}{m}\right\rfloor i &= (a - \left\lfloor\frac{a}{m}\right\rfloor m)\frac{i}{m}\\[3ex]
&= \frac{(a\% m)}{m}i
\end{aligned}
です。よって
a \rightarrow a\% m
とすれば良いです。
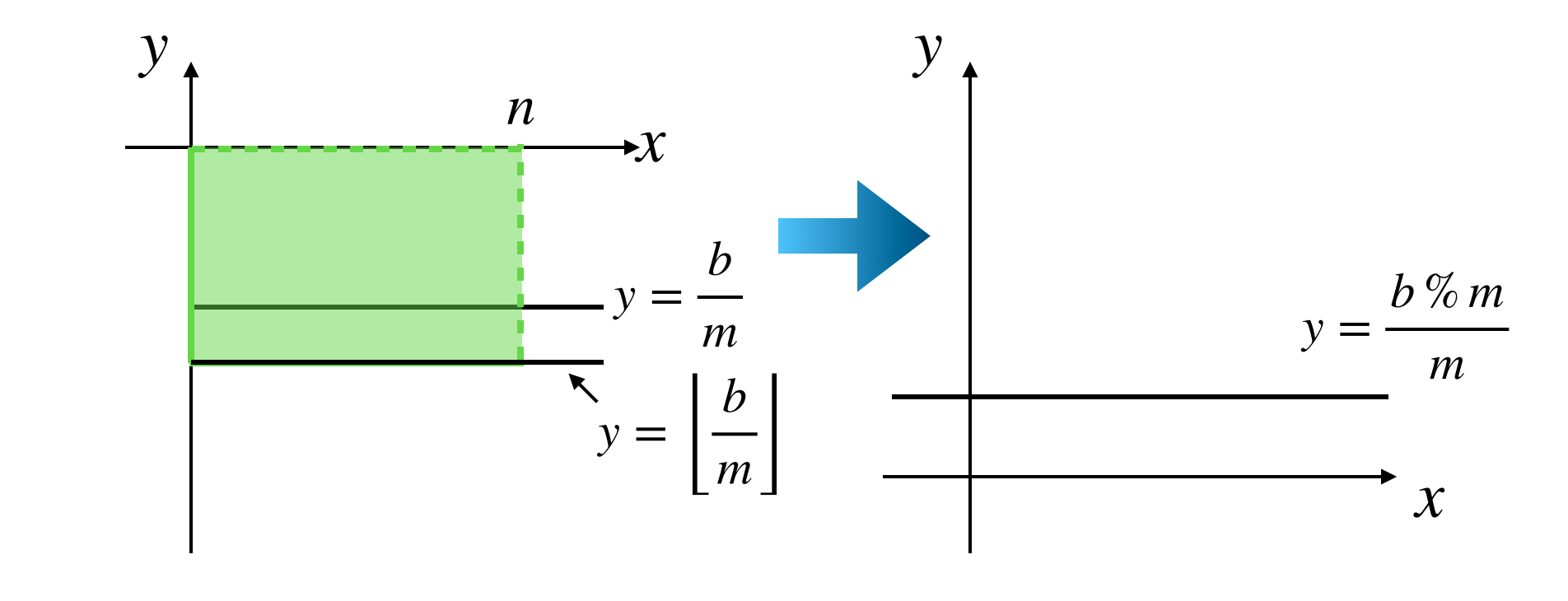
4.6. ②の領域
続いて②の領域をみていきます。この領域は下図のようになっています。
こちらは長方形なので簡単で
(領域②の格子点の個数)= n \left\lfloor\frac{b}{m}\right\rfloor
です。
①の場合と同様にこちらも数え上げた部分を取り除きます。
\frac{b}{m} - \left\lfloor\frac{b}{m}\right\rfloor = \frac{(b \% m)}{m}
なので
b \rightarrow b \% m
とすれば良いです。
4.7. 残りの領域
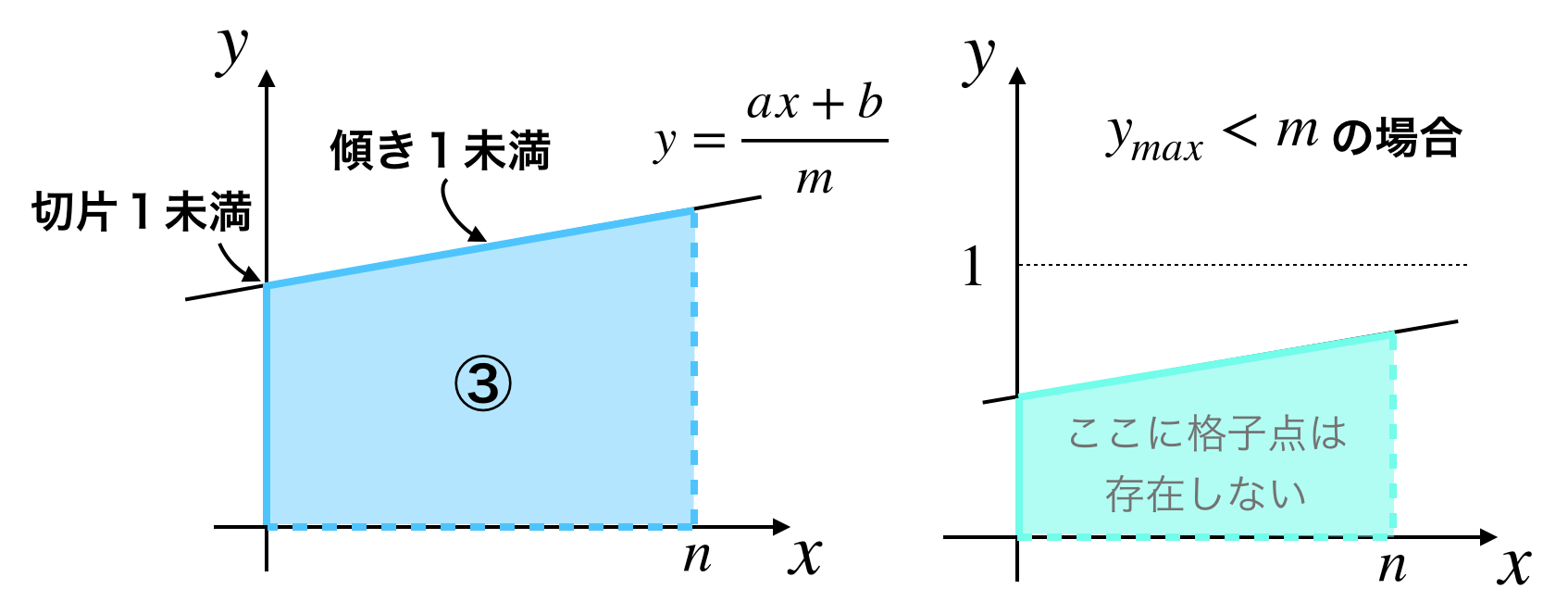
$a, b$ が $m$ 以上の場合は領域①,②を計算し $a, b$ を $m$ で割った余りで置き換えたので、この段階で $y=f(x)$ は傾きと切片がともに1未満の直線になっています。
この残りの領域を領域③と呼ぶことにします。
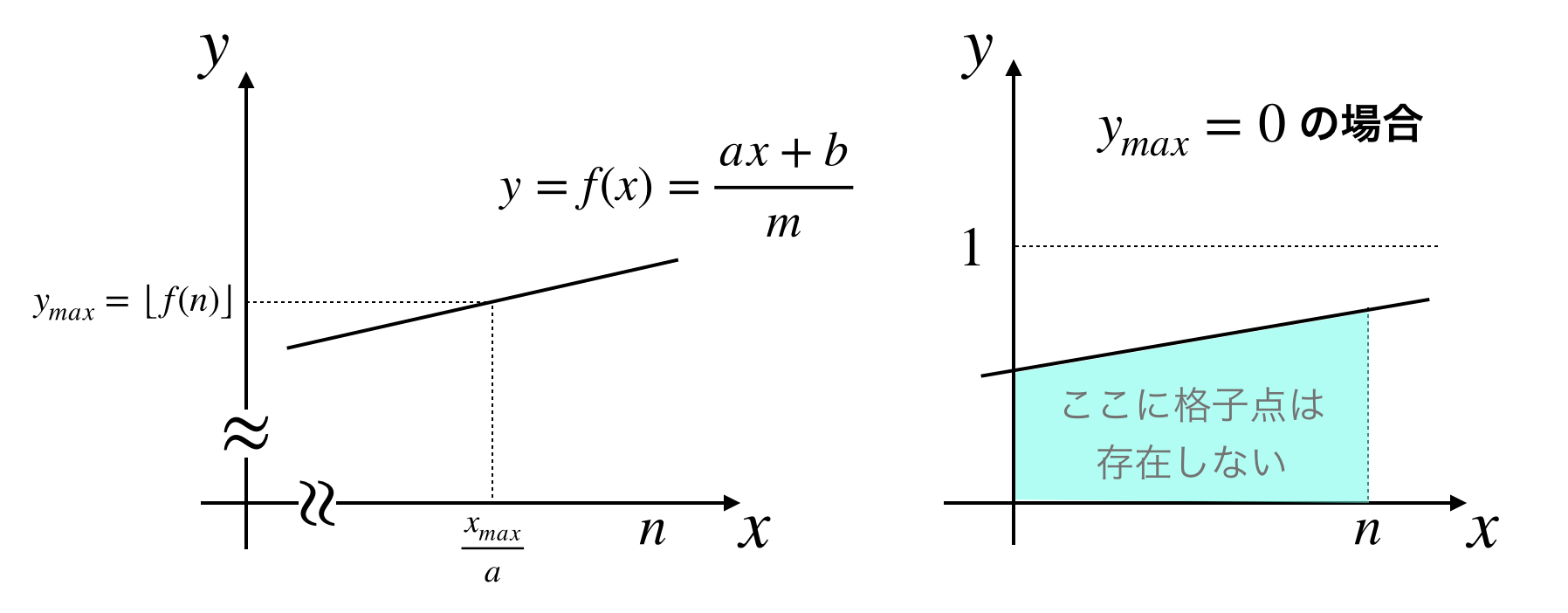
ここで新たに以下の値を定義します。
y_{max} := an + b
もし $y_{max} < m$ なら$f(n) < 1$ なので領域内に格子点は残っていません。よってここで終了となります。
そうでない場合は残りを数え上げる必要がありますが、このままでは難しいです。
数え上げができた領域①、②では次のような特徴がありました。
- ①:直線の傾きが1以上
- ②:直線の切片が1以上
よってこれらのどちらかを満たすようにしたいです。
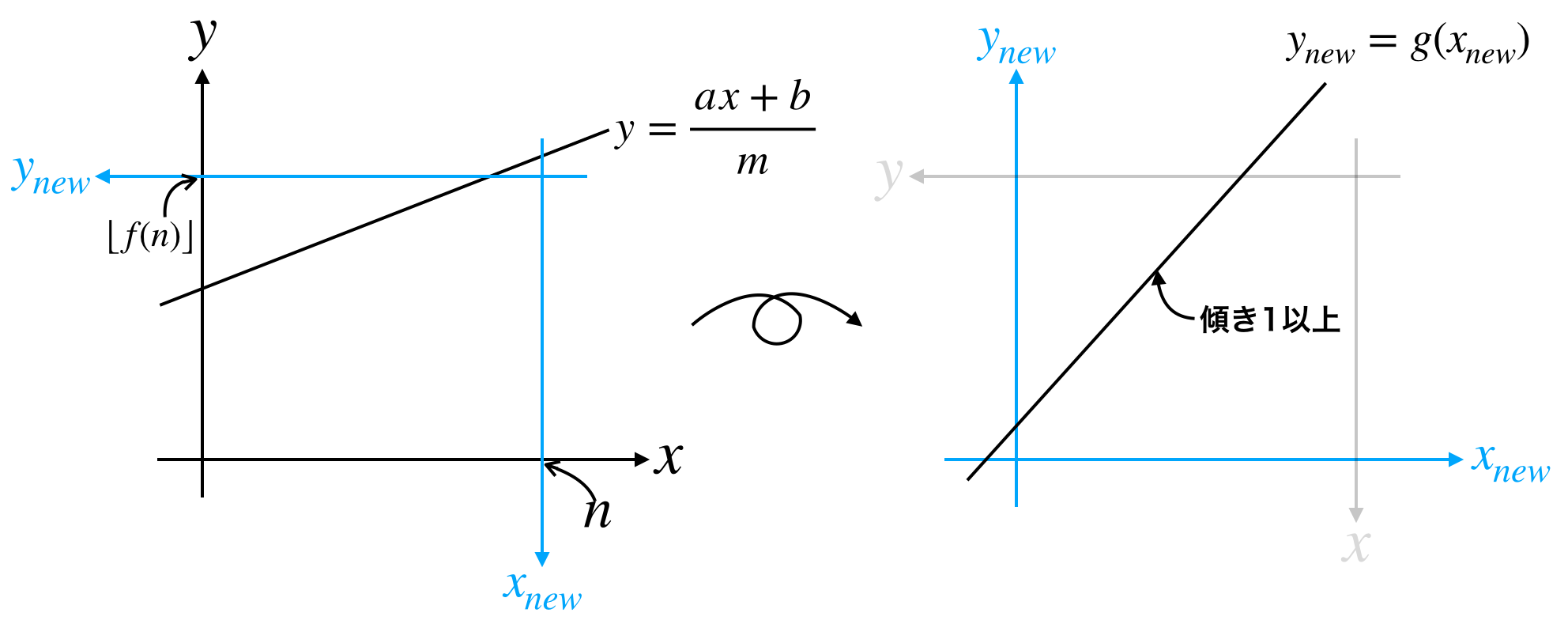
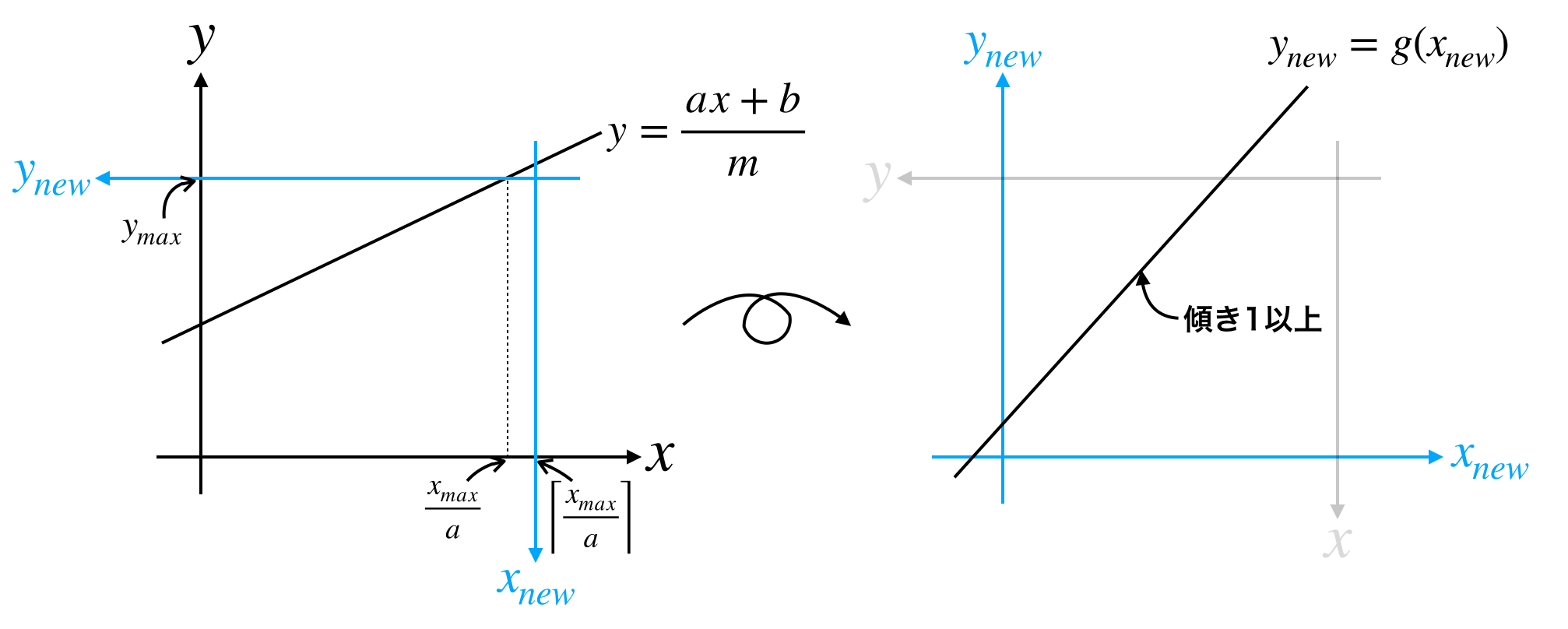
いま、直線の傾きは1未満なので下図のように新たな座標系で直線を見ることで傾きを1以上にすることができます。
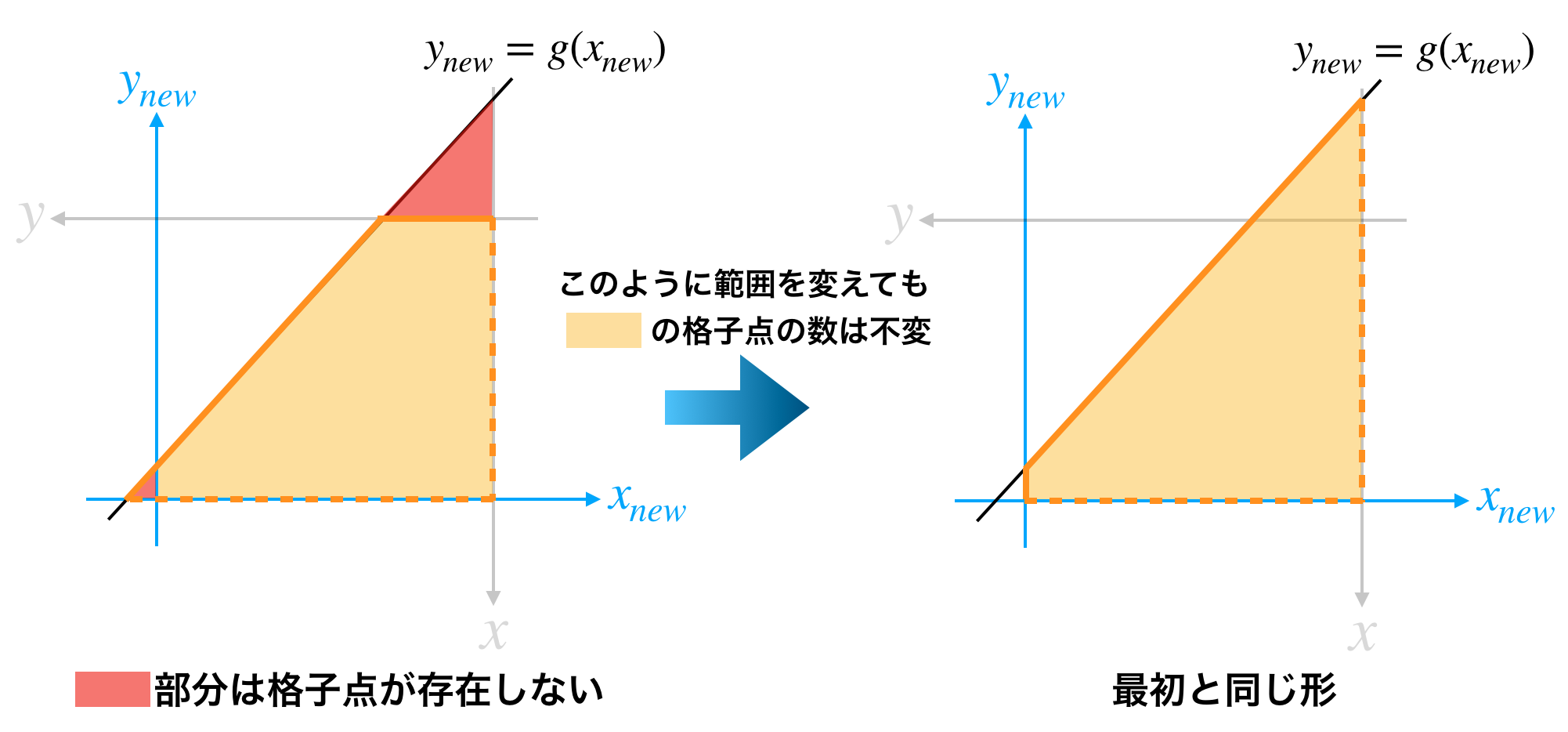
また、格子点が存在しない部分は自由に範囲を変更できるので下図のように見做すと当初の問題設定と同じ形になります。
よって最初に与えられた $(n, m, a, b)$ に対応する値を求めることで再帰的に解くことができます。
求め方は色々あると思いますがここでは以下の2通りをみていきます。
- グラフから読み取る
- 式変形で求める
グラフから読み取る方法
2つの座標系が描かれた図(2つ前の図)から読み取ります。
具体的に求めたい値は、新たな座標系で見たときの
- 全領域の右端($n$ に対応)
- 直線の傾き($a, m$ に対応)
- 直線の切片($b, m$ に対応)
です。
まず直線の傾きは元の座標系で $\frac{a}{m}$ であることから $\frac{m}{a}$ となっていることがわかります。よって $a$ と $m$ はスワップすれば良いです。
次に全領域の右端は元の座標系の $y=0$ の位置なので $\left\lfloor \frac{y_{max}}{m}\right\rfloor$ となります。
また、直線の切片は $n - (f(x) = \left\lfloor\frac{an + b}{m}\right\rfloor を満たすx)$ と読み取ることができます。
f(x) = \left\lfloor\frac{an + b}{m}\right\rfloor
を $x$ について解くと
\begin{aligned}
&\frac{ax + b}{m} = \left\lfloor\frac{an + b}{m}\right\rfloor\\[3ex]
\Leftrightarrow\; &ax + b = m\left\lfloor\frac{an + b}{m}\right\rfloor\\[3ex]
\Leftrightarrow\; &x = \frac{1}{a}\left(m\left\lfloor\frac{an + b}{m}\right\rfloor - b\right)
\end{aligned}
より切片は
\begin{aligned}
&n - \frac{1}{a}\left(m\left\lfloor\frac{an + b}{m}\right\rfloor - b\right)\\[3ex]
=&\frac{1}{a}\left(an + b - m\left\lfloor\frac{an + b}{m}\right\rfloor\right)\\[3ex]
=& \frac{(an + b) \% m}{a}\\[3ex]
=& \frac{y_{max}\% m}{a}
\end{aligned}
であることがわかります。
以上より
\begin{aligned}
n &\leftrightarrow \left\lfloor \frac{y_{max}}{m}\right\rfloor\\
m &\leftrightarrow a\\
a &\leftrightarrow m \\
b &\leftrightarrow y_{max}\% m
\end{aligned}
と対応していることがわかりました。
式変形で求める方法
元の座標系と新たな座標系の関係式を用いて式変形し元の $(n, m, a, b)$ に対応する値を求めます。
元の座標系からみた座標 $(x,y)$ を新たな座標系からみた座標 $(x_{new},y_{new})$ で表すと
\left\{
\begin{aligned}
x &= -y_{new} + n\\[2ex]
y &= -x_{new} + \left\lfloor \frac{y_{max}}{m}\right\rfloor
\end{aligned}
\right. \;\;\;\cdots (*)
です。
まず、新しい座標系での全領域の右端は元の座標系からみて $y = 0$ なので
\begin{aligned}
&y=-x_{new} + \left\lfloor \frac{y_{max}}{m}\right\rfloor = 0\\[2ex]
&\Leftrightarrow x_{new} = \left\lfloor \frac{y_{max}}{m}\right\rfloor
\end{aligned}
となります。よって $\left\lfloor \frac{y_{max}}{m}\right\rfloor$ が $n$ に相当します。
続いて直線
y = \frac{ax+b}{m}\hspace{5ex}\cdots(**)
が新たな座標系からみたときに $x_{new}, y_{new}$ を用いてどのように表されるかをみていきます。式($*$)を用いると
\begin{aligned}
&-x_{new} + \left\lfloor \frac{y_{max}}{m}\right\rfloor= \frac{a\left(-y_{new} + n\right) + b}{m}\\[3ex]
\Leftrightarrow& ay_{new} = mx_{new} + \left(an + b - m\left\lfloor \frac{y_{max}}{m}\right\rfloor\right)\\[3ex]
\Leftrightarrow& y_{new} = \frac{mx_{new} + \left(y_{max} - m\left\lfloor \frac{y_{max}}{m}\right\rfloor\right)}{a}\\[3ex]
\Leftrightarrow& y_{new} = \frac{mx_{new} + (y_{max} \% m)}{a}
\end{aligned}
となります。これを式($**$)と見比べれば($m, a, b$)に対応する値がわかります。
以上よりやはり
\begin{aligned}
n &\leftrightarrow \left\lfloor \frac{y_{max}}{m}\right\rfloor\\
m &\leftrightarrow a\\
a &\leftrightarrow m \\
b &\leftrightarrow y_{max}\% m
\end{aligned}
と対応していることがわかりました。
4.8. floor_sum_unsignedの実装
前節までの説明では再帰的に計算できると話していましたが、interlnal_math::floor_sum_unsignedは非再帰で実装されていますのでそれに合わせて非再帰の形に書き直します。(説明に近い形の実装も載せておきます)
また、C++のunsigned long longの仕様により答えがオーバーフローする場合には $\pmod{2^{64}}$ で等しい値を返すようになっています。Pythonでの必要性はわからないのでコメントアウトしています。
def floor_sum_unsigned(n, m, a, b):
# mod = 1 << 64 # 必要なら
ans = 0
while True:
# 領域①
if a >= m:
ans += n * (n - 1) * (a // m) // 2
a %= m
# 領域②
if b >= m:
ans += n * (b // m)
b %= m
# if ans >= mod: ans %= mod # 必要なら
y_max = a * n + b
if y_max < m: break
# 領域③
n, b, m, a, = y_max // m, y_max % m, a, m
return ans
説明に近い形で再帰呼び出しを用いた実装
def floor_sum_unsigned(n, m, a, b):
ans = 0
# 領域①
if a >= m:
ans += (n - 1) * n * (a // m) // 2
a %= m
# 領域②
if b >= m:
ans += n * (b // m)
b %= m
y_max = a * n + b
if y_max < m: return ans
# 領域③
ans += floor_sum_unsigned(y_max // m, a, m, y_max % m)
return ans
4.9. a, bが負の場合
ではここから $a, b$ が負の場合を考えます。具体的には $a, b$ を0以上にしてfloor_sum_unsignedが使える形に持っていくことを目指します。
aが負の場合
$a \geq 0$ のときと同様に簡単に計算できる部分を計算します。
$b$ が正で十分に大きく $y = \left\lfloor\frac{a}{m}\right\rfloor x+ \frac{b}{m}$ が $0$ 以上のときは $a \geq 0$ の場合と変わらないことがわかると思います。
$\left\lfloor\frac{a}{m}\right\rfloor x + \frac{b}{m} < 0$ の場合はどうでしょうか。簡単のために $b = 0$ としてみると下図のようになります。
簡単に計算できる部分(領域①に相当)は求めたい部分以上の大きさになりますが、まずはこれを計算し、計算できる領域と求めたい領域の差分を後から引くことにします。そしてその差分は図からやはり $\frac{a % m}{m}x$ と表せることがわかります。
以上より、$a < 0$ の場合でも $a \geq 0$ の場合と同様に答えに
\left\lfloor\frac{a}{m}\right\rfloor \frac{(n-1)n}{2}
を加算し、
a \rightarrow a \% m
とすることで $a \geq 0$ にできることがわかりました。
bが負の場合
こちらも先ほどの $a$ の場合と同様に、$b \geq 0$ の場合と同じ計算で $b \geq 0$ とすることができます。(図は $a=0$ としています。)
4.10. 実装
では、floor_sumを実装します。
コメントアウト部分はACLの実装になります。C++では整数除算が0への丸め込みになるのでこのように書かれています。
from internal_math import floor_sum_unsigned
def floor_sum(n, m, a, b):
assert 0 <= n < 1 << 32
assert 1 <= m < 1 << 32
ans = 0
if a < 0:
# a2 = a % m
# ans -= n * (n - 1) * ((a2 - a) // m) // 2
# a = a2
ans += n * (n - 1) * (a // m) // 2
a %= m
if b < 0:
# b2 = b % m
# ans -= n * ((b2 - b) // m)
# b = b2
ans += n * (b // m)
b %= m
# この時点で a, bは0以上になっている
ans += floor_sum_unsigned(n, m, a, b)
return ans
4.11. 一つにまとめた実装
Pythonでは整数除算が負の無限大への丸め込みとなっていることから $a, b < 0$ の場合も $a, b \geq m$ の場合も同じ計算で求められるので まとめて実装することもできます。
def floor_sum(n, m, a, b):
ans = 0
while True:
if a >= m or a < 0:
ans += n * (n - 1) * (a // m) // 2
a %= m
if b >= m or b < 0:
ans += n * (b // m)
b %= m
y_max = a * n + b
if y_max < m: break
n, b, m, a = y_max // m, y_max % m, a, m
return ans
4.12. 使用例
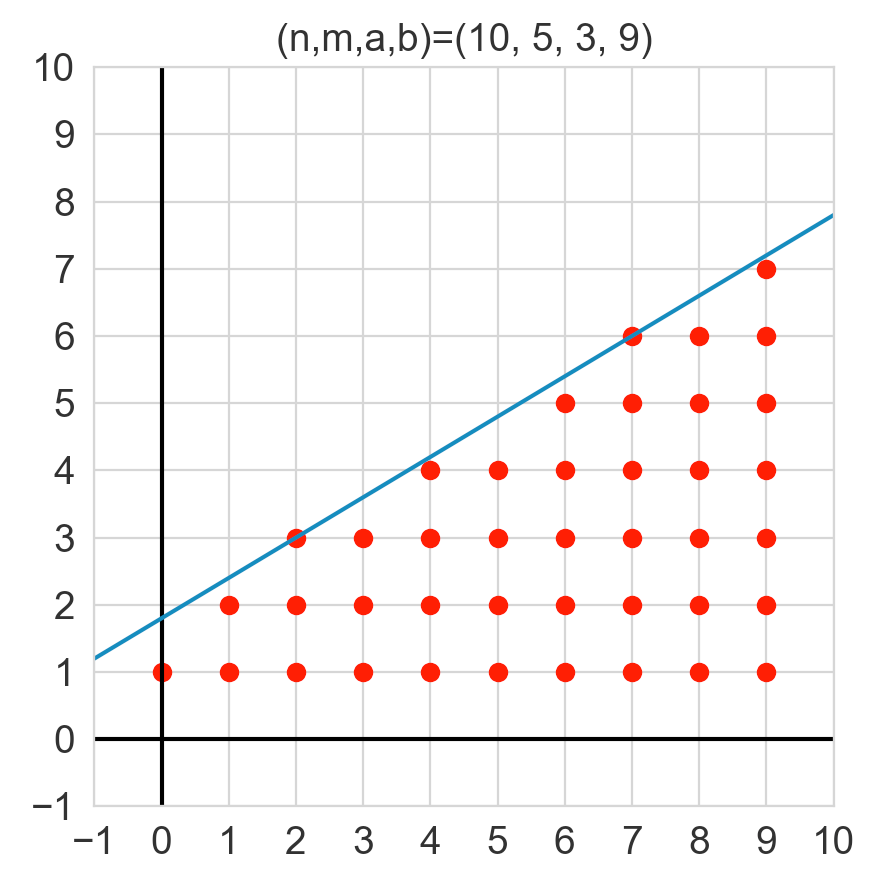
n = 10
m = 5
a = 3
b = 9
print(floor_sum(n, m, a, b)) # 41
4.13. verify用の問題
AtCoder Library Practice Contest C - "Floor Sum"
4.14. 以前のバージョンとの比較
ACL v1.3以前のfloor_sumとの比較を残しておきます。
実装方法
領域①,②は同じなのでそれ以降の説明になります。
v1.3以前(一応残していますが見なくても大丈夫です。)
さらに細かく
$a, b$ が $m$ 以上の場合は領域①,②を計算し $a, b$ を $m$ で割った余りで置き換えたので、この段階で $y=f(x)$ は傾きと切片がともに1未満の直線になっています。
ここで新たに以下の値を定義します。
- $y_{max} := f(n)を超えない最大の整数$
- $x_{max} := f(\frac{x}{a}) = y_{max}を満たすx$
すなわち
\begin{aligned}
y_{max} &= \left\lfloor \frac{an + b}{m}\right\rfloor\\[3ex]
x_{max} &= y_{max}m - b
\end{aligned}
です。
もし $y_{max}=0$ なら領域内に格子点は残っていないので終了です。
以降では $y_{max} \ne 0$ の場合を考えます。
残った領域を下図のように2つに分けそれぞれをみていきます。
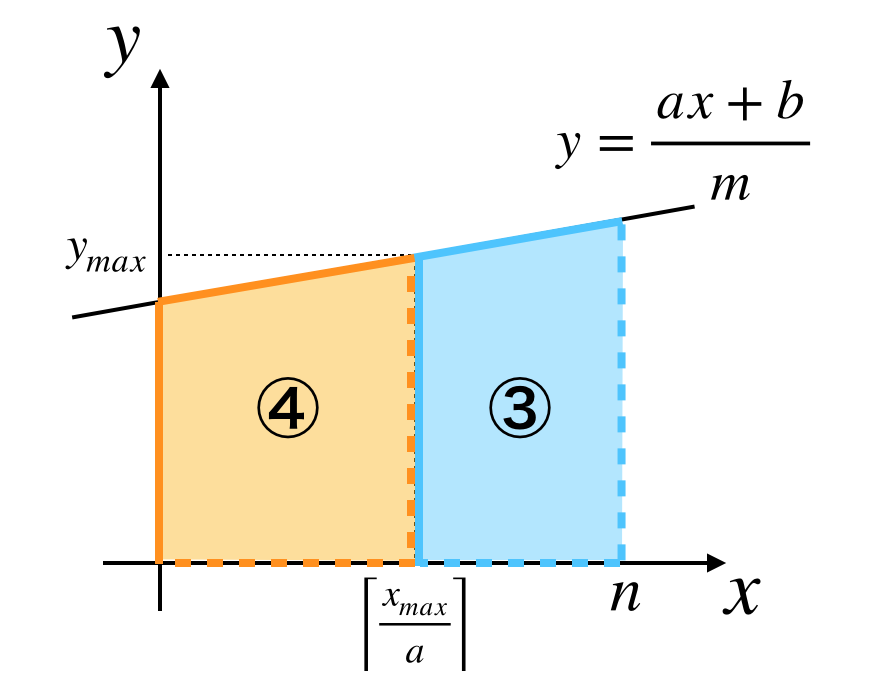
③の領域
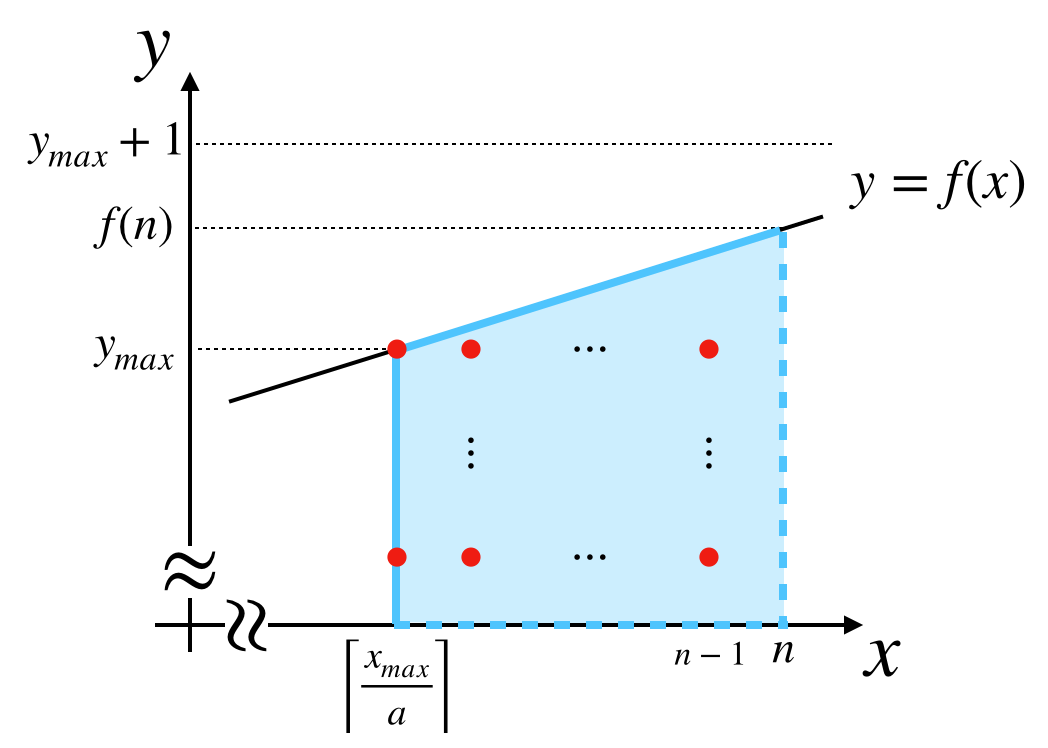
③の領域を図示すると以下のようになります。いま $f(n) - y_{max} < 1$ なので $y_{max} < y \leq f(n)$ の領域に格子点はありません。($y_{max} = f(n)$ ならそもそも③の領域はありません。)
よって
(領域③の格子点の個数)=\; \left(n - \left\lceil\frac{x_{max}}{a}\right\rceil\right)y_{max}
となります。
④の領域
④の領域はこのままでは数え上げができません。ここまで数え上げができた領域を振り返ってみると
- ①:傾きが1以上
- ②:切片が1以上(格子点が長方形に並んでいる)
- ③:格子点が長方形に並んでいる
となっていました。
いま直線の傾きは1未満なので下図のように新たな座標系で直線を見ることで傾きを1以上にすることができます。
また、格子点が存在しない部分は自由に範囲を変更できるので下図のように見做すと当初の問題設定と同じ形になります。
よって最初に与えられた $(n, m, a, b)$ に対応する値を求めることで再帰的に解くことができます。
求め方は色々あると思いますがここでは以下の2通りをみていきます。
- グラフから読み取る
- 式変形で求める
グラフから読み取る方法
2つの座標系が描かれた図(2つ前の図)から読み取ります。
求めたい値は具体的には
- 全領域の右端($n$ に対応)
- 直線の傾き($a, m$ に対応)
- 直線の切片($b, m$ に対応)
です。
まず直線の傾きは元の座標系で $\frac{a}{m}$ であることから $\frac{m}{a}$ となっていることがわかります。よって $a$ と $m$ はスワップすれば良いです。
次に全領域の右端は元の座標系の $y=0$ の位置なので $y_{max}$ となります。
また、直線の切片は $\left\lceil\frac{x_{max}}{a}\right\rceil - \frac{x_{max}}{a}$ と読み取ることができ、
\begin{aligned}
\left\lceil\frac{x_{max}}{a}\right\rceil - \frac{x_{max}}{a} &= - \left\lfloor -\frac{x_{max}}{a}\right\rfloor + \left(-\frac{x_{max}}{a}\right)\\[3ex]
&= \frac{(-x_{max}) \% a}{a}
\end{aligned}
です。
以上より
\begin{aligned}
n &\leftrightarrow y_{max}\\
m &\leftrightarrow a\\
a &\leftrightarrow m \\
b &\leftrightarrow (-x_{max})\% a
\end{aligned}
と対応していることがわかりました。
式変形で求める方法
元の座標系と新たな座標系の関係式を用いて式変形し元の $(n, m, a, b)$ に対応する値を求めます。
元の座標系からみた座標 $(x,y)$ を新たな座標系からみた座標 $(x_{new},y_{new})$ で表すと
\left\{
\begin{aligned}
x &= -y_{new} + \left\lceil\frac{x_{max}}{a}\right\rceil\\[2ex]
y &= -x_{new} + y_{max}
\end{aligned}
\right. \;\;\;\cdots (*)
です。
まず、新しい座標系での全領域の右端は元の座標系からみて $y = 0$ なので
\begin{aligned}
&y=-x_{new} + y_{max} = 0\\[2ex]
&\Leftrightarrow x_{new} = y_{max}
\end{aligned}
となります。よって $y_{max}$ が $n$ に相当します。
続いて直線
y = \frac{ax+b}{m}\hspace{5ex}\cdots(**)
が新たな座標系からみたときに $x_{new}, y_{new}$ を用いてどのように表されるかをみていきます。
式($*$)を用いると
\begin{aligned}
&-x_{new} + y_{max} = \frac{a(-y_{new} + \left\lceil\frac{x_{max}}{a}\right\rceil) + b}{m}\\[3ex]
\Leftrightarrow& -mx_{new} + my_{max} = -ay_{new} + a\left\lceil\frac{x_{max}}{a}\right\rceil + b\\[3ex]
\Leftrightarrow& y_{new} = \frac{mx_{new} + \{a\left\lceil\frac{x_{max}}{a}\right\rceil -(my_{max} - b)\}}{a}\\[3ex]
\Leftrightarrow& y_{new} = \frac{mx_{new} + \{a\left\lceil\frac{x_{max}}{a}\right\rceil -x_{max}\}}{a}
\end{aligned}
ここで
\begin{aligned}
a\left\lceil\frac{x_{max}}{a}\right\rceil -x_{max} &= -a\left\lfloor\frac{-x_{max}}{a}\right\rfloor -x_{max}\\[3ex]
&= -\{-x_{max} - (-x_{max})\%a\} - x_{max}\\[2ex]
&= (-x_{max})\%a
\end{aligned}
より
y_{new} = \frac{mx_{new} + (-x_{max})\%a}{a}
となります。これを式($**$)と見比べれば($m, a, b$)に対応する値がわかります。
以上よりやはり
\begin{aligned}
n &\leftrightarrow y_{max}\\
m &\leftrightarrow a\\
a &\leftrightarrow m \\
b &\leftrightarrow (-x_{max})\% a
\end{aligned}
と対応していることがわかりました。
実装
Pythonでの実装は以下のようになります。
def floor_sum_v1_3(n, m, a, b):
ans = 0
# 領域①
if a >= m:
ans += (n - 1) * n * (a // m) // 2
a %= m
# 領域②
if b >= m:
ans += n * (b // m)
b %= m
y_max = (a * n + b) // m
x_max = y_max * m - b
if y_max == 0: return ans
# 領域③
ans += (n - (x_max + a - 1) // a) * y_max
# 領域④
ans += floor_sum(y_max, a, m, (-x_max) % a)
# ACLでは負数の剰余に注意して以下のように書かれている
# ans += floor_sum(y_max, a, m, (a - x_max % a) % a)
return ans
4.15. 実行速度
AtCoder Library Practice Contest C - "Floor Sum" への提出は以下の通りです。
v1.4で25%程度の改善がみられます。
| version | 時間 |
|---|---|
| v1.4 | 855 ms |
| v1.4(1つにまとめた実装) | 866 ms |
| v1.3以前 | 1162 ms |
5. おわりに
今回は主にcrtとfloor_sumについてみてきました。floor_sumは問題を見て使えると判断するのが難しそうですね。
説明の間違いやバグ、アドバイス等ありましたらお知らせください。