0. はじめに
2020年9月7日にAtCoder公式のアルゴリズム集 AtCoder Library (ACL)が公開されました。
私はACLに収録されているアルゴリズムのほとんどが初見だったのでいい機会だと思い、アルゴリズムの勉強からPythonでの実装までを行いました。
この記事では internal_math をみていきます。
internal_mathはACLの内部で使われる数論的アルゴリズムの詰め合わせで内容は以下の通りです。
| 名称 | 概要 |
|---|---|
| safe_mod | 整数 $x$ の正整数 $m$ による剰余($x \% m$)。ただし $0 \leq x \% m < m $ を満たす。 |
| barrett | 高速な剰余演算。 |
| pow_mod | $x^n \pmod{m}$ の計算。 |
| is_prime | 高速な素数判定。 |
| inv_gcd | 整数 $a$ と正整数 $b$ の最大公約数 $g$ および $xa \equiv g \pmod{b}$ となる $x$ の計算。ただし $0 \leq x < \frac{b}{g} $ を満たす。 |
| primitive_root | $m$ を法とする原始根。 |
| floor_sum_unsigned | $0$ 以上の整数 $n, a, b$ と自然数 $m$ について $\sum_{i=0}^{n-1}{\left\lfloor\frac{ai+b}{m}\right\rfloor}$ の計算。 |
本記事ではこれらの内、
- safe_mod
- pow_mod
- inv_gcd
- barrett
を扱います。なお、constexpr(定数式)自体については触れません。
本記事で扱わない
- is_prime
- primitive_root
については以下の記事で扱っています。よろしければそちらもご覧ください。
【internal_math編②】AtCoder Library 解読 〜Pythonでの実装まで〜
なお、floor_sum_unsigned は math 内の floor_sum の補助的な役割なので説明は
【math編】AtCoder Library 解読 〜Pythonでの実装まで〜
で行なっています。
対象としている読者
- ACLの内部で使われている数学系アルゴリズムを知りたい方。
- ACLのコードを見てみたけど何をしているのかわからない方。
- C++はわからないのでPythonで読み進めたい方。
参考にしたもの
C++のドキュメントです。
@drkenさんによる、競技プログラミングで問われるあまりの求め方がまとめられた記事です。非常にわかりやすいです。
ユークリッドの互除法を数式で記述する参考にしました。
Barrett reduction の参考記事です。
1. safe_mod
整数 $x$ の正整数 $m$ による剰余 $x \% m$ を考えます。
1.1. C++での剰余演算
C++では以下のようになります。
#include <bits/stdc++.h>
using namespace std;
int main(){
cout << " 7 % 3 = " << 7 % 3 << endl; // 7 % 3 = 1
cout << "-7 % 3 = " << -7 % 3 << endl; // -7 % 3 = -1
return 0;
}
注目するのは2つ目で、 $x$ が負のとき剰余も負となります。これは
- 商は0に向かって丸め込まれる
- $(x/m)*m+x\%m==x$ を満たす
によるものです。(参考)
1.2. 実装
safe_mod は剰余 $x \% m$ の値を $0 \leq x \% m < m $ に収める関数です。これは剰余演算の結果が負の場合に $m$ を加算することで達成できます。
Pythonでの実装は以下のようになります。
def safe_mod(x, m):
x %= m
if x < 0: x += m
return x
なお、Pythonでは正整数 $m$ による剰余は$0 \leq x \% m < m $ となることが保証されているのでこの実装は不要です。(これはPythonでの整数除算 "//" が負の無限大に向かって丸め込まれるからです。)
# safe_modによる剰余演算
print(f'safe_mod(7, 3) = {safe_mod(7, 3)}') # safe_mod(7, 3) = 1
print(f'safe_mod(-7, 3) = {safe_mod(-7, 3)}') # safe_mod(-7, 3) = 2
# 算術演算子%による剰余演算
print(f' 7 % 3 = {7 % 3}') # 7 % 3 = 1
print(f'-7 % 3 = {-7 % 3}') # -7 % 3 = 2
2. pow_mod
整数 $x$ および自然数 $n, m$ について $x^n \pmod{m}$ の計算を考えます。
2.1. 素朴な方法
指数 $n$ が自然数の場合 $x^n$ は $x$ を $n$ 回かけたものですので、その通りに実装すると以下のようになります。
def naive_pow_mod(x, n, m):
r = 1 # 結果を入れる変数
for _ in range(n):
r *= x
r %= m # mで割ったあまりを求める
return r
x = 3
n = 4
m = 5
print(naive_pow_mod(x, n, m)) # 1
しかし、$n$ が $10^9$ 程度の場合はどうでしょうか。上記の方法では2つの問題点が考えられます。
- $10^9$ 回程度の乗算が必要になる
- 計算の過程で値が非常に大きくなる
これらによって非常に長い計算時間が必要になります。そしてこれらの問題点を解決することで高速に $x^n \pmod{m}$ を計算するpow_modが実装できます。
2.2. 問題点1の解決策: 繰り返し二乗法
繰り返し二乗法(バイナリ法とも呼ばれます)はその名の通り二乗を繰り返します。これによって大きな指数の計算を少ない計算回数で行えます。
- $x$ を二乗して $x^2$ を得る。
- $x^2$ を二乗して $x^3$を計算することなく $x^4$ を得る。
- $x^4$ を二乗して $x^5, x^6, x^7$を計算することなく $x^8$ を得る。
$\cdots$
という具合です。具体例として $n = 50$ の場合を見てみましょう。いま、指数が2のべき乗の場合($x, x^2, x^4, \cdots$)の結果が得られているので $x^{50}$ をこれらで表すことを考えます。
50=32 + 16 + 2
なので
x^{50}=x^{32}\cdot x^{16}\cdot x^{2}
とかけます。よって、 $x^{50}$ は
- $x^{32}$ を求めるまでに5回
- それらを掛け合わせる3回(結果の値として1を用意した場合)
の合計8回の乗算で求められます。
これらの手続きを機械的に行うためには二進数を活用するのが有効です。二進数の定義からいって当たり前ですが、整数 $n$ を構成する2のべき乗(上の例では32, 16, 2)は $n$ を二進数表記したときに'1'であるビットに対応しています。そこで $n$ を下位ビットから見ていき、'1'の場合に対応する $x^{(2のべき乗)};;$ をかけることで求める値が得られます。
Pythonでの実装は以下のようになります。
# 繰り返し二乗法によるべき乗計算
def binary_pow_mod(x, n, m):
r = 1 # 結果を入れる変数
y = x # x^(2のべき乗) を入れる変数
while n:
if n & 1: r = r * y #最下位ビットが1なら乗算する
y = y * y
n >>= 1 #右シフトで次のビットを見る
r %= m
return r
2.3. 問題点2の解決策: mod演算の性質
コンピューターは(人間から見て)非常に高速に計算でき、またPythonではメモリが許す限り大きな整数を扱うことができますが、それでもやはり大きな桁の計算は時間がかかります。例えば $3^{1000000000}$ を繰り返し二乗法を用いて計算する場合、最終的に
3^{536870912} \times 3^{463129088}
を計算することになります。もし欲しいものが $x^n$ を自然数 $m$ で割ったあまりならば、mod演算の性質を利用してこのような大きな数字の演算を回避することができます。使う性質は次のものです。
乗算は(最後にmodを取りさえすれば)いつ何度でもmodをとって良い
$x$ を $m$ で割ったあまりは常に $0 \leq x \% m < m $ の範囲に収まるので乗算をするたびにmodをとることで常に $m$ 未満の値同士の演算にすることができます。
2.4. 実装
pow_modは繰り返し二乗法にmod演算の性質を使ったものです。これは先ほど実装したbinary_pow_modに少し手を加えることで実装できます。
def pow_mod(x, n, m):
if m == 1: return 0 # 1で割った余りは常に0
r = 1
y = x % m # mで割ったあまりにする
while n:
if n & 1: r = r * y % m # mで割ったあまりにする
y = y * y % m # mで割ったあまりにする
n >>= 1
return r
なお、Pythonでは組み込み関数のpow()がpow_modに相当するのでこの実装は不要です。
# 素朴な方法での実装
print(naive_pow_mod(3, 4, 5)) # 1
#print(naive_pow_mod(13, 1000000, 1000000007)) # 終わりません
# 繰り返し二乗法を用いた実装
print(binary_pow_mod(13, 1000000, 1000000007)) # 735092405 このくらいならなんとか計算できます
#print(binary_pow_mod(13, 1000000000, 1000000007)) # 終わりません
# 繰り返し二乗法 + modの性質を用いた実装(ACLのpow_modに相当)
print(pow_mod(13, 1000000000, 1000000007)) # 94858115
# Pythonの組み込み関数powを用いた計算
print(pow(13, 1000000000, 1000000007)) # 94858115
3. inv_gcd
整数 $a$ と正整数 $b$ に対し、
- 最大公約数 $\gcd(a, b)$
- $xa \equiv \gcd(a, b) \pmod{b}$ となる $x$
を計算します。ただし $x$ は $0 \leq x < \frac{b}{\gcd(a, b)} $ を満たします。
3.1. ユークリッドの互除法
まずは $a$ と $b$ の最大公約数から見ていきましょう。
最大公約数を計算するアルゴリズムとしてユークリッドの互除法というものがあります。
Pythonでの実装は以下のようになります。
def gcd(a, b):
if b == 0: return a
return gcd(b, a % b)
以降では $a > b$ とします。$a < b$ であったとしても $0 \leq a \% b < b$ より再帰的に呼ばれる $\gcd(b, a\%b)$ は必ず第一引数の方が大きくなるので問題ありません。
最大公約数がユークリッドの互除法によって計算できるのは以下の2つによるものです。
- $\gcd(a, b) = \gcd(b, a \% b)$
- $a \ne 0$ に対し $\gcd(a, 0) = a$
1.の証明は@drkenさんの記事にありますのでそちらをご覧ください。
2.は $a$ が 0 の約数であることから明らかです。
1.の主張は強力です。いま $a > b$ かつ $b > a \% b$ なので1.によると
$a$ と $b$ の最大公約数を求める問題はより小さな数の最大公約数を求める問題に変えることができる
となります。また、$a \% b \geq 0$ なので1.を繰り返し用いることでいつか必ず $\gcd(g, 0)$ という形になります。そして 2.よりこの $g$ こそが求める $a$ と $b$ の最大公約数です。
3.2. ユークリッドの互除法を数式で記述する
ユークリッドの互除法を数式で表します。
$a=r_0, b=r_1$ とし、$r_k$ を $r_{k+1}$ で割った商を $q_k$ と書くとき
\begin{aligned}
r_0 &= q_0r_1 + r_2\\
r_1 &= q_1r_2 + r_3\\
\cdots\\
r_{n-1} &= q_{n-1}r_n + 0
\end{aligned}
となり、このようにして得られる $r_n$ が $a$ と $b$ の最大公約数でした。
上の式を行列を用いて表現すると
\begin{aligned}
\begin{pmatrix}
r_0\\
r_1
\end{pmatrix}
&=
\begin{pmatrix}
q_0 & 1\\
1 & 0\\
\end{pmatrix}
\begin{pmatrix}
r_1\\
r_2
\end{pmatrix}\\
\begin{pmatrix}
r_1\\
r_2
\end{pmatrix}
&=
\begin{pmatrix}
q_1 & 1\\
1 & 0\\
\end{pmatrix}
\begin{pmatrix}
r_2\\
r_3
\end{pmatrix}\\
\cdots\\
\begin{pmatrix}
r_{n-1}\\
r_n
\end{pmatrix}
&=
\begin{pmatrix}
q_{n-1} & 1\\
1 & 0\\
\end{pmatrix}
\begin{pmatrix}
r_n\\
0
\end{pmatrix}
\end{aligned}
となります。これらをまとめて書くと
\begin{pmatrix}
r_0\\
r_1
\end{pmatrix}
=
\begin{pmatrix}
q_0 & 1\\
1 & 0\\
\end{pmatrix}
\begin{pmatrix}
q_1 & 1\\
1 & 0\\
\end{pmatrix}
\cdots
\begin{pmatrix}
q_{n-1} & 1\\
1 & 0\\
\end{pmatrix}
\begin{pmatrix}
r_n\\
0
\end{pmatrix}
\;\;\;\;\cdots(*)
が得られます。
いま、$i=0, 1, \cdots,n-1$ に対し
Q_i=
\begin{pmatrix}
q_i & 1\\
1 & 0
\end{pmatrix}
とおくと行列式は
\begin{aligned}
\det(Q_i) &= q_i \cdot 0 - 1\cdot1\\
&=-1
\end{aligned}
なので、逆行列 $Q_i^{-1}$ が存在し
\begin{aligned}
Q_i^{-1} &= -
\begin{pmatrix}
0 & -1\\
-1 & q_i
\end{pmatrix}
=
\begin{pmatrix}
0 & 1\\
1 & -q_i
\end{pmatrix}
\end{aligned}
です。したがって式($*$)は
\begin{pmatrix}
\gcd(a, b)\\
0
\end{pmatrix}
=
\begin{pmatrix}
0 & 1\\
1 & -q_{n - 1}
\end{pmatrix}
\begin{pmatrix}
0 & 1\\
1 & -q_{n - 2}
\end{pmatrix}
\cdots
\begin{pmatrix}
0 & 1\\
1 & -q_{0}
\end{pmatrix}
\begin{pmatrix}
a\\
b
\end{pmatrix}
\;\;\;\;\cdots(**)
となります。
3.3. 拡張ユークリッドの互除法
さて、inv_gcdで得られる2つ目のもの
- $xa \equiv \gcd(a, b) \pmod{b}$ となる $x$
を見ていきましょう。これは整数 $y$ を用いて
ax + by = \gcd(a, b)
と書くこともできます。よって、この式を満たす $x$ を求めればよいことになります。
ところで、前節で得られた式$(**)$において
\begin{pmatrix}
x & y\\
u & v
\end{pmatrix}
=
\begin{pmatrix}
0 & 1\\
1 & -q_{n - 1}
\end{pmatrix}
\begin{pmatrix}
0 & 1\\
1 & -q_{n - 2}
\end{pmatrix}
\cdots
\begin{pmatrix}
0 & 1\\
1 & -q_{0}
\end{pmatrix}
とおくと
\begin{pmatrix}
\gcd(a, b)\\
0
\end{pmatrix}
=
\begin{pmatrix}
x & y\\
u & v
\end{pmatrix}
\begin{pmatrix}
a\\
b
\end{pmatrix}
となります。つまり、この $x, y$ は
ax + by = \gcd(a, b)
を満たします。したがって、式$(** )$を用いて$\gcd(a,b)$を計算することで、その過程において $xa \equiv \gcd(a, b) \pmod{b}$ となる $x$ が得られることがわかります。このようにして整数 $(x, y)$ を求めるアルゴリズムを拡張ユークリッドの互除法と言います。
3.4. inv_gcd実装の準備①
ユークリッドの互除法は $r_0=a, r_1=b$ とし、手続き
\begin{pmatrix}
r_{i+1}\\
r_{i+2}
\end{pmatrix}
=
\begin{pmatrix}
0 & 1\\
1 & -q_{i}\\
\end{pmatrix}
\begin{pmatrix}
r_{i}\\
r_{i+1}
\end{pmatrix}
を $r_{i+2}$ が $0$ になるまで繰り返すことでした。そして
\begin{pmatrix}
x_i & y_i\\
u_i & v_i
\end{pmatrix}
=
\begin{pmatrix}
0 & 1\\
1 & -q_{i}
\end{pmatrix}
\begin{pmatrix}
0 & 1\\
1 & -q_{i-1}
\end{pmatrix}
\cdots
\begin{pmatrix}
0 & 1\\
1 & -q_{0}
\end{pmatrix}
を同時に計算することで $ax + by = \gcd(a, b)$ を満たす$(x, y)$を求めるのが拡張ユークリッドの互除法です。
では実際に計算する過程を見ていきましょう。
$a, b$ が与えられたとき、まず $a\%b$ が $0$ かどうかを確認します。もし $0$ ならば、以降の手続きをすることなく
\begin{aligned}
\gcd(a, b) = b\\
x=0
\end{aligned}
であることがわかります。
$a, b$ が与えられたときの各変数の初期状態は以下のようになります。
\begin{aligned}
r_0 = a, \;\;r_1&=b\\\\
\begin{pmatrix}
x_{-1} & y_{-1}\\
u_{-1} & v_{-1}
\end{pmatrix}
&=
\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}
\end{aligned}
$(x, y, u, v)$ の初期状態が単位行列なのは $i=0$ においてこれらの変数が
\begin{pmatrix}
x_0 & y_0\\
u_0 & v_0
\end{pmatrix}
=
\begin{pmatrix}
0 & 1\\
1 & -q_{0}
\end{pmatrix}
を満たすためです。
次に各変数の従う漸化式を見ていきます。
まず、$r_{i+1}, r_i$ から $q_i$ が求まります。
q_i = \left\lfloor\frac{r_i}{r_{i+1}}\right\rfloor
次にこれを用いて他の変数の遷移がわかります。
\begin{aligned}
r_{i+2} &= r_i - q_ir_{i+1}\\\\
\begin{pmatrix}
x_i & y_i\\
u_i & v_i
\end{pmatrix}
&=
\begin{pmatrix}
0 & 1\\
1 & -q_{i}
\end{pmatrix}
\begin{pmatrix}
x_{i-1} & y_{i-1}\\
u_{i-1} & v_{i-1}
\end{pmatrix}
\end{aligned}
終了条件は $r_{i+2}=0$ です。このとき
\begin{aligned}
r_{i+1} = \gcd(a, b)\\
ax_{i}+by_{i}=\gcd(a, b)
\end{aligned}
となります。
3.5. inv_gcd実装の準備②
$ax+by=\gcd(a, b)$ は不定方程式なので解が無数に存在します。ここでは拡張ユークリッドの互除法によって得られた解 $x$ が $ |x| < \frac{b}{\gcd(a, b)} $ を満たすことを示します。
そのためにまず、以下を示します。
$i \geq 0$ に対し、
r_{i+1}|u_i|+r_{i+2}|x_i|\leq b
が成り立つ。
用いるのは$r_i, x_i, u_i$ の漸化式
\begin{aligned}
r_{i+2} &= r_i - q_ir_{i+1}\\
x_i &= u_{i-1}\\
u_i &= x_{i-1} - q_iu_{i-1}
\end{aligned}
と絶対値の性質
|x - y| \leq |x| + |y|
です。
数学的帰納法により示します。
$i=0$ のとき、
\begin{aligned}
r_{1}|x_0|+r_{2}|u_0|&=b|1|+r_2|0|\\
&=b\\
&\leq b
\end{aligned}
で満たします。
$i=k$ のとき、
r_{k+1}|u_k|+r_{k+2}|x_k|\leq b
を満たすと仮定すると $i=k+1$ のとき、
\begin{aligned}
&r_{k+2}|u_{k+1}|+r_{k+3}|x_{k+1}| \\
=\;& r_{k+2}|x_{k} - q_{k+1}u_{k}| + (r_{k+1} - q_{k+1}r_{k+2})|u_k|\\
\leq\;&r_{k+2}|x_k|+q_{k+1}r_{k+2}|u_k|+r_{k+1}|u_k|-q_{k+1}r_{k+2}|u_k|\\
=\;& r_{k+1}|u_k|+r_{k+2}|x_k|\\
\leq\;&b
\end{aligned}
となり満たします。
以上より、$i \geq 0$ に対し、
r_{i+1}|u_i|+r_{i+2}|x_i|\leq b
が成り立つことが示されました。
この結果を使って $|x|$ を評価しましょう。いま、$r_{n+2}=0$ であったとします。すなわち、
\begin{aligned}
r_{n+1}&=\gcd(a,b)\\
x_{n}a&\equiv\gcd(a, b)\pmod{b}
\end{aligned}
となります。先ほど示した不等式において $i=n-1$ の場合を考えます。すると、
\begin{aligned}
(左辺) &= r_{n}|u_{n-1}|+r_{n+1}|x_{n-1}|\\
&\geq r_{n}|u_{n-1}|\\
&> r_{n+1}|u_{n-1}|\\
&= \gcd(a, b)|x_n|
\end{aligned}
であり、$a\%b\ne0$より $\gcd(a, b)\ne b$ なので、拡張ユークリッドの互除法によって得られた $x_n$ は
|x_n|< \frac{b}{\gcd(a, b)}
を満たすことが示されました。
また、$x_n < 0$ であった場合
x = x_n + \frac{b}{\gcd(a, b)}
とすることで $0 \leq x < \frac{b}{\gcd(a, b)}$ となる $x$ を得ることができます。この $x$ は
\begin{aligned}
xa &= (x_n + \frac{b}{\gcd(a, b)})a\\
&=x_na+\rm{lcm(a, b)}\\
&\equiv x_na \pmod{b}
\end{aligned}
より確かに求める解になっています。ここで、$\rm{lcm}\it{(a, b)}$ は $(a, b)$ の最小公倍数です。
3.6. inv_gcd実装の準備③
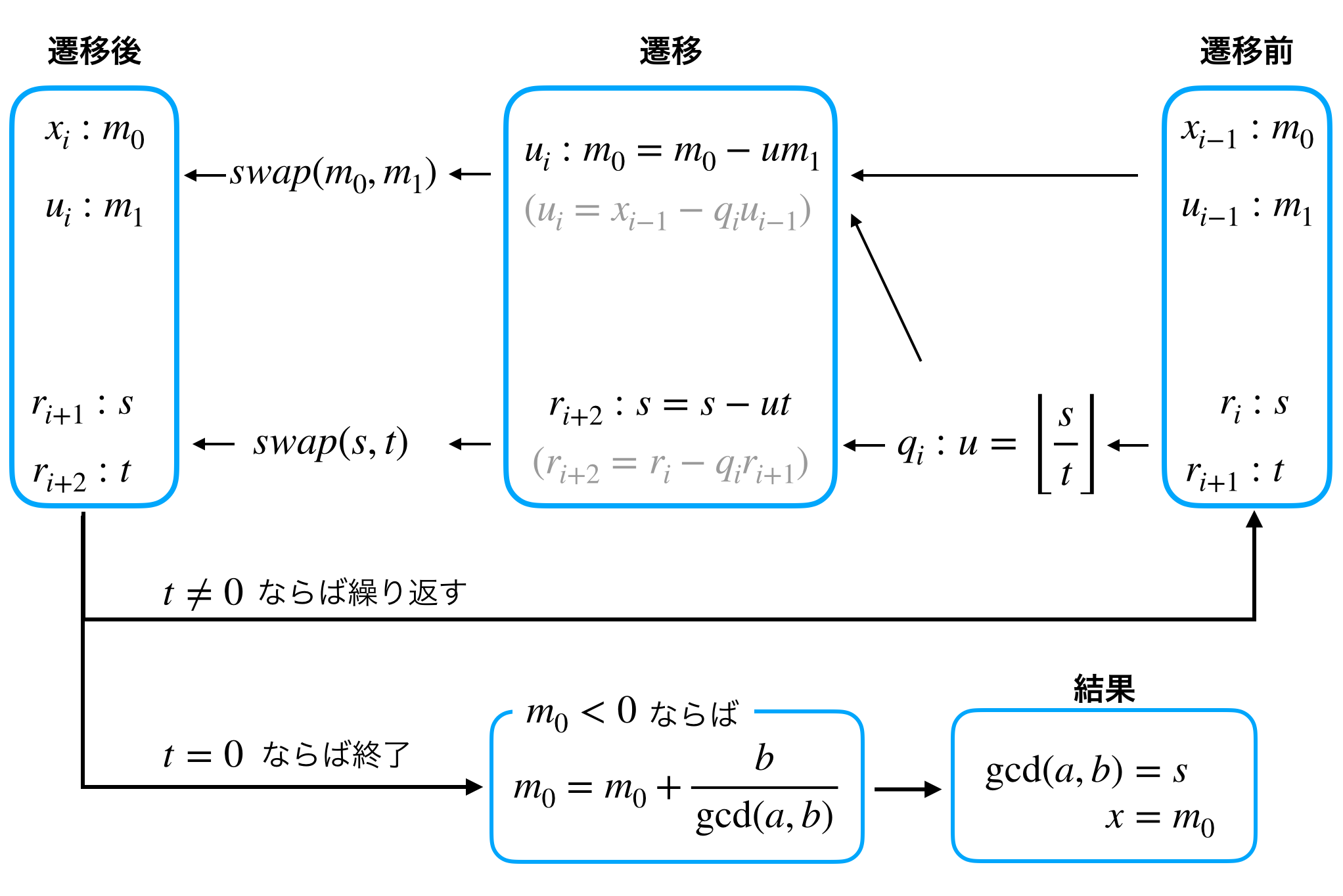
inv_gcd実装の準備①では各変数に添字をつけて数列のようにそれぞれの遷移を追ってきましたが、実装上は古い値を保持する必要はないのでよりコンパクトに書くことができます。
ここからはACLで実際に使われている変数名に沿っていきます。
まずは必要な変数を確認しましょう。
$r_i$ は三項間漸化式なので変数は二つ必要になります。これらを $s, t$ とします。$q_i$ は一つあればよいのでこれを $u$ とします。$(x_i, y_i, u_i, v_i)$ ですが、漸化式を見ると$(x_i, u_i)$ と $(y_i, v_i)$ は独立であることがわかります。いま、欲しいのは $x$ なので $(y_i, v_i)$ は保持する必要がありません。そこで、$(x_i, u_i)$ を $(m_0, m_1)$ とします。
準備①でも述べたとおり、$a, b$ が与えられたときまず $a\%b$ を確認します。これが $0$ ならば以降の手続きをすることなく
\begin{aligned}
\gcd(a, b) = b\\
x=0
\end{aligned}
で終わりです。よって、以降では $a\%b\ne 0$ の場合を見ていきます。
初期状態は
\begin{aligned}
s &= r_1 = b\\
t &= r_2 = r_0 - \left\lfloor\frac{r_0}{r_{1}}\right\rfloor r_1 = a \% b\\\\
m_0 &= x_0 = u_{-1} = 0\\
m_1 &= u_0=x_1 - \left\lfloor\frac{r_0}{r_{1}}\right\rfloor u_{-1} = 1
\end{aligned}
です。ここから、$t=0$ となるまで下図の遷移を繰り返します。
3.7. 実装
前節で述べた通りに実装していきます。なお、ACLにおいて safe_mod を用いている部分はPythonにおいて同等の機能である算術演算子 % で代用します。
def inv_gcd(a, b):
a %= b
if a == 0: return b, 0
# 初期状態
s, t = b, a
m0, m1 = 0, 1
while t:
# 遷移の準備
u = s // t
# 遷移
s -= t * u
m0 -= m1 * u
# swap
s, t = t, s
m0, m1 = m1, m0
if m0 < 0: m0 += b // s
return s, m0
print(inv_gcd(3, 5)) # (1, 2)
print(inv_gcd(20, 15)) # (5, 1)
4. barrett
「ある自然数 $m$ が与えられるので、$m$ で割ったあまりを答えよ」という問題ではオーバーフロー対策や、多倍長整数であったとしても巨大な数によって計算速度が低下することを避けるため、何かの演算をするたびに $m$ で割ったあまりをとるということをよくします。あまりを求めるためには割り算をする必要がありますが、割り算は四則演算の中でコンピューターが苦手としている演算であり、他の演算よりも時間がかかってしまいます。Barrett reductionは「ある決まった自然数(定数) $m$ で割ったあまりをとる演算」を高速化するアルゴリズムです。
ACLにおいては $0 \leq a < m, 0 \leq b < m$ となる整数 $a, b$ に対して
(a \cdot b) \;\% \;m
を高速化する目的で使われています。
以降では $z :=a\cdot b \; (0 \leq z < m^2)$ とおき、$z \% m$ を考えます。
4.1. アイデア
いくら割り算が苦手と言っても、あまりを求める際には避けては通れません。なぜならあまりは
z\%m = z - \left\lfloor z \div m\right\rfloor m
と表されるからです。また、一般的な数による割り算は苦手でも2のべき乗による割り算は得意です。2進数で動くコンピューターにとって、「$2^k$ で割る」ということは「右に k シフトする」だけでよいからです。
よって、あまりを求める演算を高速化するために、苦手な演算(一般的な自然数による割り算)を得意な演算(足し算、引き算、掛け算、シフト演算)に置き換えることを考えます。
「$m$ で割る」は「$\frac{1}{m}$をかける」と等価です。いま、自然数 $k, n$ を用いて十分良い精度で
\frac{1}{m} \approx \frac{n}{2^k}
と近似できたとします。すると、
\begin{aligned}
z\%m &= z - \left\lfloor z \cdot \frac{1}{m}\right\rfloor m\\
&= z - \left\lfloor z \cdot \frac{n}{2^k}\right\rfloor m\\
&= z - \{(z \cdot n) >> k\}m
\end{aligned}
となり、得意な演算(引き算、掛け算、シフト演算)だけであまりを表すことができました。
4.2. k, n の決め方
では、自然数 $k, n$ はどのように決めれば良いでしょうか。もし $m$ が 2 のべき乗であったなら、
\frac{1}{m} = \frac{n}{2^k}
を満たす自然数 $k, n$ が存在します。よって以降では、$m$ が 2 のべき乗でない場合を考えます。
まず、$k$ が満たすべき条件を見ていきます。いま、$2^k < m$ となる $k$ を選んだとすると、$n=1$ がもっとも良い近似となりますが、これはほとんどの場合良い近似ではありません。よって、$k$ は
2^k > m
となるように選ぶ必要があります。
$k$ が決まれば $n$ は
n \simeq \frac{2^k}{m}
となるように選ぶだけです。よって
n=\left\lceil \frac{2^k}{m}\right\rceil\; or\; \left\lfloor \frac{2^k}{m}\right\rfloor
となります。ACLでは天井関数を採用していますが、一般的には床関数を選ぶことが多いようです。
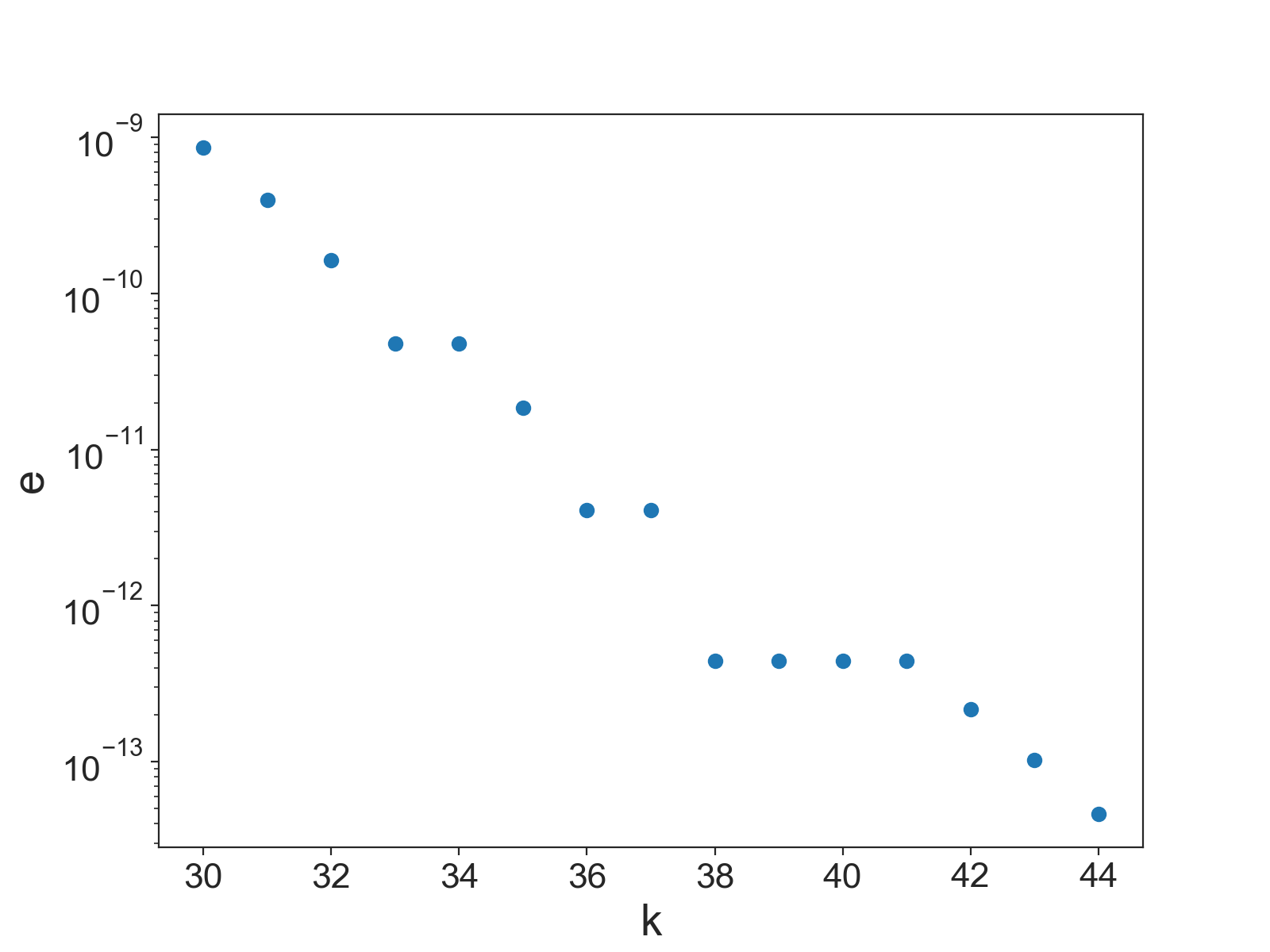
さて、$k$ の下限はわかりましたが、具体的な値はどう決めれば良いでしょうか。いま、近似の指標として
e = \frac{n}{2^k} - \frac{1}{m}
を導入します。具体例として競技プログラミングでよく問われる $m=1000000007 ;;(10^9 + 7)$ の場合を見てみましょう。このとき、$k$ の下限は
\begin{aligned}
k_{min} &= \lceil\log_2{1000000007}\rceil\\
&= 30
\end{aligned}
です。そこで、$k \geq 30$ の $k$ について $e$ を計算してみると下図のようになります。
$e$ は $k$ に対して単調非増加ですので、$k$ は大きいほど良いことがわかりました。ただし、$k$ が大きくなるほど扱う数が大きくなり、その分計算に時間がかかるのでとにかく大きくすれば良いというわけではなさそうです。
ACLでは $k=64$ としています。これによって $n$ も
n = \left\lceil \frac{2^{64}}{m}\right\rceil
と決まります。
補足1
$n$ は 正確には
n =
\begin{cases}
0 & (m = 1)\\
\left\lceil \frac{2^{64}}{m}\right\rceil & (m \geq 2)
\end{cases}
となっています。
ACLにおいて入力 $a, b$ は既に $m$ で割ったあまりとなっていることが要求されます。$m = 1$ のとき、$a = b = 0$ より
\begin{aligned}
z \% m &= z - \{(z \cdot n) >> k\}m\\
&= 0 - 0 \cdot 1\\
&= 0
\end{aligned}
となるので問題ありません。よって以降では $m \geq 2$ とします。
補足2
割り算が入っていると思われるかもしれませんが、いま $m$ は事前に与えられる定数なので $n$ もまた事前計算によって定数となります。
4.3. なぜ k=64 ?
では、なぜ $k=64$ なのでしょうか。
ひとつの理由として unsigned long long (符号なし8バイト整数)で扱える最大値が $2^{64} - 1$ であることが挙げられます。
そしてもうひとつの理由としては、$k=64$ であれば4バイト整数の入力 $a, b$ と4バイト整数の法 $m$ に対して $(a\cdot b)\% m$ を正しく計算できる、というものがあります。
これを示すためには以下のことを示せば良いでしょう。
$2 \leq m < 2^{31}$ なる整数 $m$ と $0 \leq a, b < m$ なる整数 $a, b$ に対し積 $z:=a \cdot b$ が整数 $q, r$ を用いて
z = qm + r\;\;\;\;\;(0 \leq r < m)
と表されたとき、次の関係式が成立する。
q \leq \{(z \cdot n) >> 64\} < q + 2
ここで、
n=\left\lceil \frac{2^{64}}{m}\right\rceil
であり、>>は右シフト演算である。
これが示された場合、
\{(z \cdot n) >> 64\}=q \;\;\; \rm{or} \;\;\; q + 1
となります。すなわち $z \% m$ を正確に計算できたか、もしくは正確な値より $m$ だけ小さく計算してしまったかのどちらかになります。よって、もし得られた結果が負の値であった場合には $m$ を加算することで正しい結果が得られます。
それでは証明していきます。
まずは下限から見ていきます。いま、
\frac{n}{2^{64}} \geq \frac{1}{m}
であるから、
\begin{aligned}
\left\lfloor\frac{zn}{2^{64}}\right\rfloor &\geq \left\lfloor\frac{z}{m}\right\rfloor\\
&= \left\lfloor q + \frac{r}{m}\right\rfloor\\
&= q + \left\lfloor\frac{r}{m}\right\rfloor\\
&= q
\end{aligned}
したがって、
\{(z \cdot n) >> 64\} \geq q
となります。
つづいて、上限を見ていきます。$nm$ が $0 \leq l < m$ なる整数 $l$ を用いて
\begin{aligned}
nm &= \left\lceil \frac{2^{64}}{m}\right\rceil m\\
&= 2^{64} + l
\end{aligned}
とかけることを利用すると
\begin{aligned}
zn &= (qm + r)n\\
&= qnm + nr\\
&= 2^{64}q + (ql + nr)
\end{aligned}
が得られます。ここで、$z < m^2$ より $q < m$ であるから
\begin{aligned}
ql+nr &< m^2 + nm\\
&< m^2 + 2^{64} + m\\
&= 2^{64} + m(m+1)\\
&< 2 \cdot 2^{64}
\end{aligned}
となるので
\begin{aligned}
zn &< 2^{64}q + 2 \cdot 2^{64}\\
&= 2^{64}(q + 2)
\end{aligned}
したがって、
\{(z \cdot n) >> 64\} < q+2
が成り立ちます。
以上より
q \leq \{(z \cdot n) >> 64\} < q + 2
が示されました。
4.4. 実装
では実装していきます。まずクラスBarrettを作成しコンストラクタを実装します。法 $m$ を確認するためのメソッドも用意しておきます。
class Barrett:
# @param 1 <= m < 2^31
def __init__(self, m):
self._m = m
self.im = -(-(1<<64) // m) if m > 1 else 0
# mを返すメソッド
def umod(self):
return self._m
変数imがこれまでの $n$ に相当します。ACLでは固定長整数の性質を活かした書き方をしていますが、Pythonは多倍長整数なのでif文で場合分けをして処理します。
このように $m$ による割り算が必要な部分を事前計算し定数として保持しておくことで高速化します。
ではメソッド "mul" を実装します。これが $a, b$ に対し $(a \cdot b )\% m$ を返すメソッドです。
class Barrett:
# __init__()
# umod()
def mul(self, a, b):
assert 0 <= a < self._m
assert 0 <= b < self._m
z = a * b
v = z - ((z * self.im)>>64) * self._m
if v < 0: v += self._m
return v
m = 1000000007
bt = Barrett(m)
a = 12345678
b = 87654321
print(bt.mul(a, b)) # 14799574
print((a * b) % m) # 14799574
4.5. 実用性は...
察している方もいるかと思いますが、 Pythonでは組み込みの算術演算子 % を素直に使った方が速いです。
巨大な数になれば効果が出てくるかもしれませんが、競技プログラミングで扱うような数では(Pythonでは)必要なさそうです。
5. おわりに
今回はACLの内部で使われるアルゴリズムを見てきました。数式を追うのが大変でしたが、理解が深まりました。
internal_mathのなかで今回触れなかったものについてはinternal_math編②で書いていますので、よろしければそちらもご覧ください。
説明の間違いやバグ、アドバイス等ありましたらお知らせください。