今回は仕事で名前を聞いたり、過去にはStable Diffusionで利用されて一躍有名になったLoRAについて原著の論文を読んでいきます。
In this Article
- LoRAでは何をしているか理解する
- LoRAがなぜ爆発的に普及したか理解する
事前に以下の記事を読んでAttentionの基本を抑えると理解しやすくなります
今回は以下のLoRAの論文を読んで理解していきます!
LoRAとは
Low-Rank Adaptationの略
LoRA (Low-Rank Adaptation) は、既存モデルの重み(Pretrained Weights)を完全に凍結し、その重みに加える “変化” だけを低ランク(Low-Rank)行列で表現して学習することで、少ない計算量でファインチューニングを可能にする手法。
そもそもファインチューニングとは?
すでに学習済みの大規模モデル(Pretrained Model)をベースとして、
追加のデータでモデルを再学習させ、特定タスクに適応させること。
LoRAの論文では以下のように紹介されており、すべてのパラメータを更新することであると書かれている。
Such adaptation is usually done via fine-tuning, which updates all the parameters of the pre-trained model.
理想は新しいデータで全パラメータを学習し直すことかもしれないが、そうするとコストが莫大にかかる。
このためなんとか低コストでファインチューニングできないか?と考案されたのがLoRA
元の論文では
As we pre-train larger models, full fine-tuning, which retrains all model parameters, becomes less feasible.
とあるように、LLMの巨大な重み行列を追加学習することを避けたい意図が書かれている。
LoRAが解決した課題
論文ではLoRA以前のファインチューニングについて以下のような課題を挙げている。
- モデルの深さが増えることで推論時間(レイテンシ)が長くなる
- モデルが扱える有効なシーケンス長を短くしてしまう
- フルファインチューニングと比較して性能が劣る
(一応)論文ではこれらを解決できたと記載がある。
LoRAが着目したポイント
ここが今回なぜLoRAなのか?に至るポイントです。
We take inspiration from Li et al. (2018a); Aghajanyan et al. (2020) which show that the learned over-parametrized models in fact reside on a low intrinsic dimension.
別の論文では、巨大なモデルでも学習で動いている重みの変化は実はもっと小さい次元にreside(留まっている)のではないか?と言っている
We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”, leading to our proposed Low-Rank Adaptation (LoRA) approach.
上記結果を受け、モデルのファインチューニングの重みの変化も本質的にはもっと小さな次元の更新で済むのでは?という仮説を得た結果LoRAのアプローチに至ったと書いてある。
“intrinsic rank” (本質的ランク)とあるので重み更新 ΔW が実際に必要とする自由度(ランク)が非常に小さいという意味と解釈。
ファインチューニングで更新される重みの変化は低ランクでも近似できたということであって元の重みに冗長性があるということは言っていない。
ファインチューニングの出力の差は実際は小さな重みの変化だけで生まれているということ
LoRAで何をするか
少し長くなるが引用
ここで述べられていることがLoRAが便利な理由になります。
先ほどの引用の直後に概要が書かれている
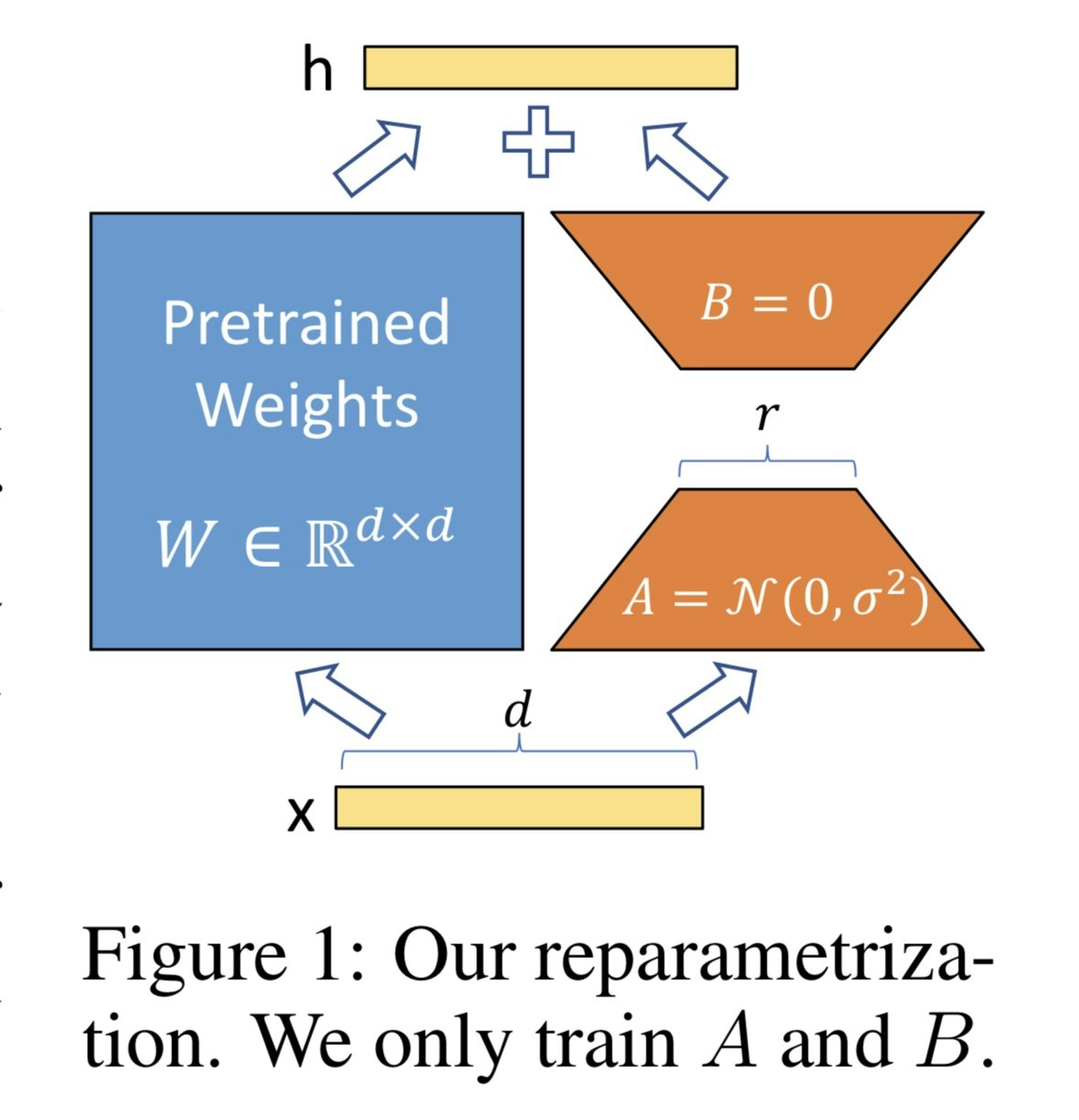
LoRA allows us to train some dense layers in a neural network indirectly by optimizing rank decomposition matrices of the dense layers’ change during adaptation instead, while keeping the pre-trained weights frozen, as shown in Figure 1.
つまり、元の学習ずみの重みを固定(図の左側)し、その重みに加える変化 ΔW をΔW = A×B(低ランク分解)で表現する。追加で学習するのは小さな行列 A(d×r)と B(r×d)だけということ。
図で示されているAとBについて
- A:入力を r 次元に圧縮する(bottleneck)
- B:r 次元から元の次元に戻す
- r : ボトルネックの次元。LoRA における低ランク近似のランクを決める値。
Aを平均0・分散σ²の正規分布で初期化することで微小な勾配が生まれ、学習が進むようになるらしい。
LoRAで追加する重みは「元の出力を新しいデータに方向修正する部品」になるように学習される。
ΔWを差し替えることが可能なため、元の重みを変更してしまうファインチューニングでは不可能だった、追加する重みを差し替えて別々のタスクにパッと適応させることができる
これがLoRAの一番大きな特徴ではないかと思っている。
LoRAの内容を行列で確認
3×4 の行列を元の重みとし、r=1 の行列で LoRA を適用する場合、以下のようになる
この例では、元の重みは12パラメータなの対し、ファインチューニングで学習するパラメータは7で済んでいる。
- 元の重み
W =
\begin{bmatrix}
w_{11} & w_{12} & w_{13} & w_{14} \\
w_{21} & w_{22} & w_{23} & w_{24} \\
w_{31} & w_{32} & w_{33} & w_{34}
\end{bmatrix}
- 入力をr次元に射影する行列
学習時に更新される
A =
\begin{bmatrix}
a_{11} & a_{12} & a_{13} & a_{14}
\end{bmatrix}
- r次元から元の重みと同じ出力次元に射影する行列
学習時に更新される
B =
\begin{bmatrix}
b_{11} \\
b_{21} \\
b_{31}
\end{bmatrix}
- 推論時に追加される重み(A×B)
元の重みに加算する必要があるので、A×Bで元の行列サイズと同じになる。
\Delta W = AB =
\begin{bmatrix}
\Delta w_{11} & \Delta w_{12} & \Delta w_{13} & \Delta w_{14} \\
\Delta w_{21} & \Delta w_{22} & \Delta w_{23} & \Delta w_{24} \\
\Delta w_{31} & \Delta w_{32} & \Delta w_{33} & \Delta w_{34}
\end{bmatrix}
実際には勾配爆発を防ぐスケーリングを行うため以下の式となる
\begin{aligned}
\Delta W &= \frac{\alpha}{r} \, B A \\
W_{\text{adapted}} &= W + \Delta W = W + \frac{\alpha}{r} \, B A
\end{aligned}
このスケーリングは分散に比例して大きくなる値(今回はr)で割ってやる事で大小の関係性を保ったまま、極端に大きい/小さい値をなくすための統計的工夫。
今回はΔWがr個の要素の積の和なので、rが増えると値も上下にブレやすくなる。
どの重み行列に適用するか
※論文はまだ続きますが一旦ここで最後にします。
LoRAは重みの更新をより少ない計算量で可能にする手法。ということはtransformerの中のいろいろな重みに適用できる。
Attention入力のQKVや、
- Wq(Query 重み)
- Wk(Key 重み)
- Wv(Value 重み)
出力のOやフィードフォワードネットワークなど。 - Wo: 出力線型層
論文のSection7.1の最後には
Note that putting all the parameters in ΔWq or ΔWk results in significantly lower performance, while adapting both Wq and Wv yields the best result.
とあり、QueryやKeyではなく、QueryとValueに同時にLoRAを適用すると最も効果があったと書かれている
最後に
今回はLoRAの論文を読んでみました。
Stable Diffusionで利用されて一躍有名になったので気になっていました。
今回はそもそも何?という部分に焦点をあてたので、論後半に書かれている示唆や結果を時間をとってもっとちゃんと読んでみようと思います。