はじめに
この記事は、
第一回 為替の値動きは本当に正規分布に従うのか?PyMC2を使って確かめる
第二回 為替の値動きはコーシー分布に従うのか?PyMC2を使って確かめる
の続きです。よろしければご覧ください。
前々回が正規分布、前回がコーシー分布と仮定して為替の値動きのパラメータを推測してみました。
前回の記事でt分布もロングテールというコメントを頂いたので、今回は非心t分布と仮定してPyMC2でパラメータを推測していきます。コメント有難うございました。
実行環境
maxOS High Sierra
Anaconda Python3.5 の仮想環境
Jupyter Notebook
PyMC2
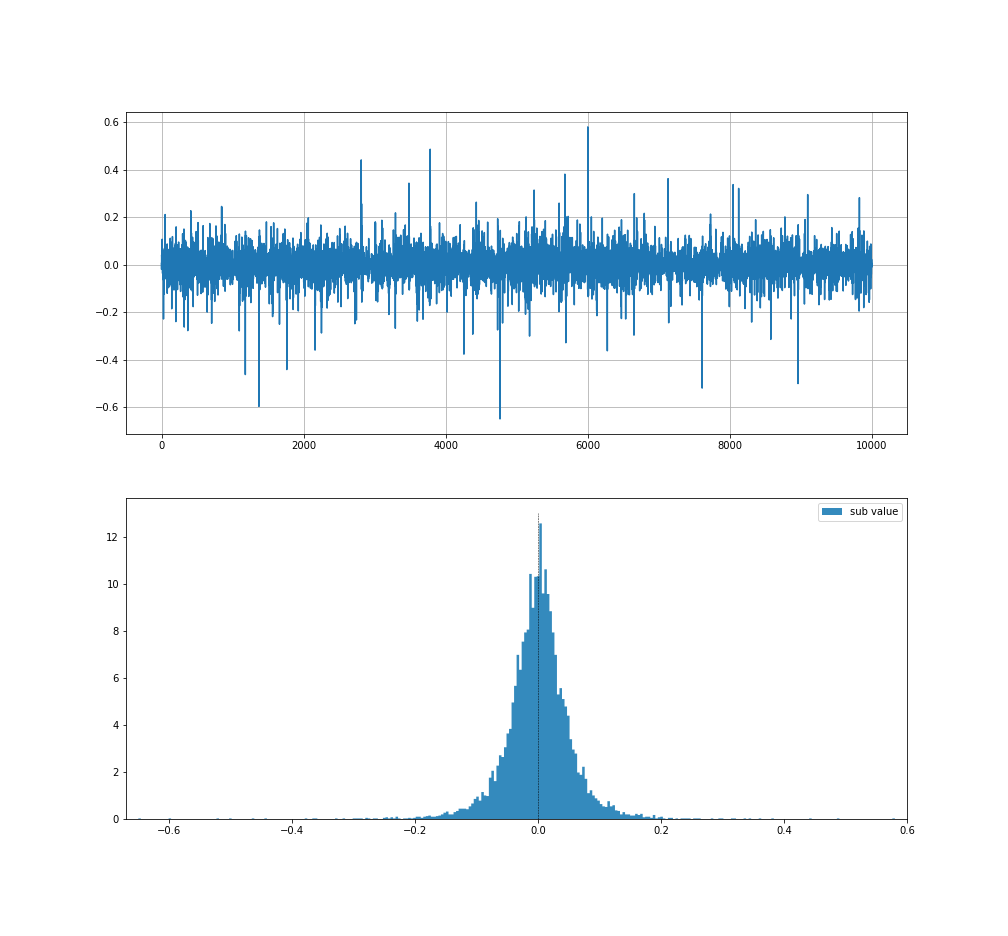
使用する為替データは、USD-JPYの15分足2003.09.01〜2017.11.17の終値で、最新から10000区間分を使います。
t分布とは
t分布は、母集団の平均、分散が不明で、標本サイズが小さい時に母集団の平均を推定する際やt検定の際に使用される確率分布です。
正規分布の裾野を広げたような形をしています。
ピークを揃えるとこのような感じになっています。
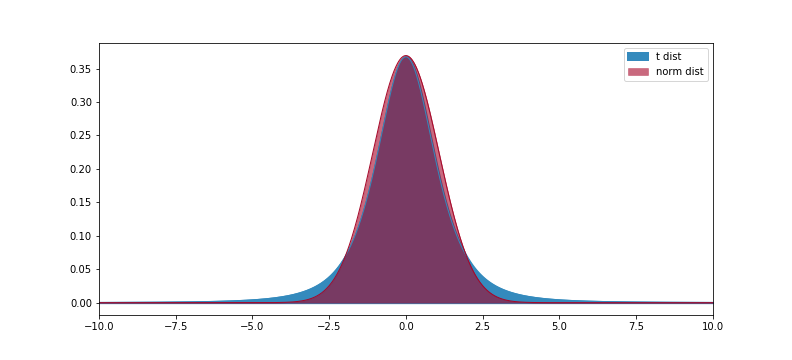
自由度というパラメータが存在して、自由度 = 1 の時コーシー分布、自由度 = ∞ の時正規分布になっています。
今回は非心t分布を使用します。非心t分布はt分布を一般化したものです。
為替データを見る
今までと同じものを使用します。
このヒストグラムについて非心t分布(Non-central Student’s T )と仮定してパラメータを推測していきます。
PyMC2で非心t分布のパラメータを推測する
PyMC2で非心t分布を使用するために、
Location parameter(平均のようなもの), Scale parameter(標準偏差のようなもの), 自由度の3つが必要です。
なので、事前分布として
Location parameter(mu):平均0 標準偏差0.05の正規分布
Scale parameter(lam):0~10の一様分布
自由度(nu):見当がつかないので、0~1000までの一様分布
にしました。
Location parameterとScale parameterを推測できるので、今回はt分布ではなく非心t分布を使用します。
事前分布のグラフは正規分布と一様分布なのでほぼ今までと同じなので省略させていただきます。
PyMC2の実行
# 非心t分布で近似
mu = pm.Normal("mu", 0, 1. / 0.5**2) #Location parameter
lam = 1. / pm.Uniform("lam", 0, 10)**2 #Scale parameter 色々試した所、正規分布の時と同じく精度になっている
nu = pm.Uniform("nu", 0, 1000) #自由度 検討がつかないので、0~1000までの一様分布
# データが非心t分布から得られたとする
obs_3 = pm.NoncentralT("obs_3", mu, lam, nu, value=sub_value, observed=True)
# モデルの作成
model_3 = pm.Model([obs_3, mu, lam, nu])
mcmc_3 = pm.MCMC(model_3)
mcmc_3.sample(100000, 70000, 3)
figsize(11, 6)
mu_samples = mcmc_3.trace("mu")[:]
lam_samples = mcmc_3.trace("lam")[:]
nu_samples = mcmc_3.trace("nu")[:]
plt.subplot(311)
plt.hist(mu_samples, bins=30, alpha=0.8, histtype="stepfilled",
color=colors[0], density=True)
plt.title("mu samples")
plt.grid()
plt.subplot(312)
plt.hist(lam_samples, bins=30, alpha=0.8, histtype="stepfilled",
color=colors[0], density=True)
plt.title("lam samples")
plt.grid()
plt.subplot(313)
plt.hist(nu_samples, bins=30, alpha=0.8, histtype="stepfilled",
color=colors[0], density=True)
plt.title("nu samples")
plt.grid()
plt.tight_layout()
※注意
PyMC2のホームページの 9. Probability distributions には noncentral_t_like とあるので、Noncentral_t で使えるかと思いきや、NoncentralT でした。何故なのかは不明。
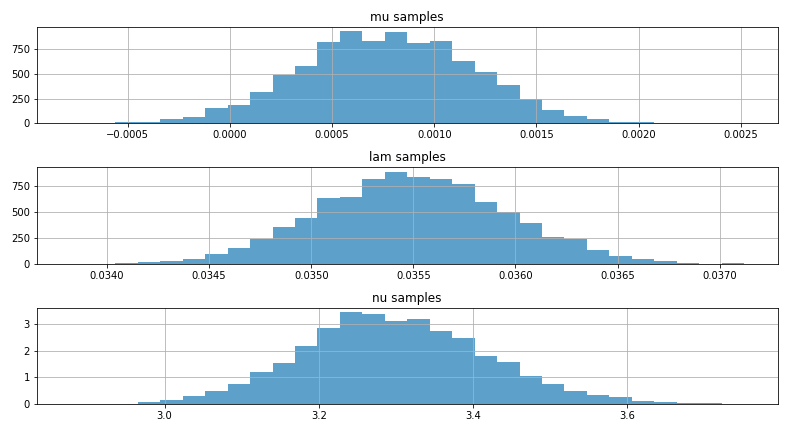
事後分布の結果
mu, lam, nu の事後分布はこのようになりました。
収束してそうですね。いやMCMC素晴らしい。
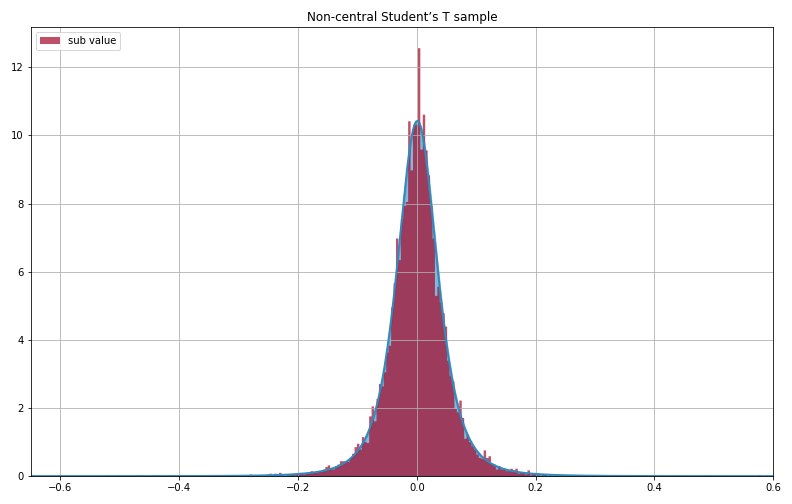
得られた事後分布から非心t分布を描く
毎回グラフはscipyで描いているのですが、scipyの非心t分布(nct)にはパラメータが4つ必要で、ncは歪みを指定するパラメータなのですがPyMC2に存在しません。もしかしたらPyMC2の非心t分布(のnoncentral_t_likeの部分)は、t分布の平均と分散を動かすことができるだけかもしれません。
実際、PyMC2の非心T分布から値を生成しても歪んだ形にはなりませんでした。
scipyでnctの色々とヒストグラムを生成して実験したみたところ、ncもmuにすると求めたいものに近くなったので今回はそうしてみます。
また、ncを0にするとscipyのt分布と同じものになると思われます。
figsize(11, 7)
mu_mean = mu_samples.mean() #muの平均
lam_mean = lam_samples.mean() #lamの平均
nu_mean = nu_samples.mean() #nuの平均
print("mu_mean", mu_mean)
print("lam_mean", lam_mean)
print("nu_mean", nu_mean)
x = np.linspace(-0.65, 0.6, 500)
# scipyの非心t分布(nct)には、パラメータが4つ必要
a_y = stats.nct.pdf(x, nu_mean, mu_mean, mu_mean, lam_mean)
# 非心t分布を描く
plt.plot(x, a_y, lw=2, color=colors[0])
plt.fill_between(x, 0, a_y, color=colors[0], linewidth=2,
edgecolor=colors[0], alpha=0.6)
plt.hist(sub_value, bins=300, histtype="stepfilled", alpha=0.7,
density=True, color=colors[1], label="sub value")
plt.title("Non-central Student’s T sample")
plt.xlim(-0.65, 0.6)
plt.legend(loc="upper left")
plt.tight_layout()
plt.grid()
最終結果
mu_mean 0.0007713048467022937
lam_mean 0.03549970342210986
nu_mean 3.2986686930281315
前回、前々回と比べてだいぶ当てはまりが良いように見えます。
結果から言える事
前回のコーシー分布に比べて、±(0.05~0.1)辺りが改善されています。
ただ、極端な値の辺りを拡大してみると、
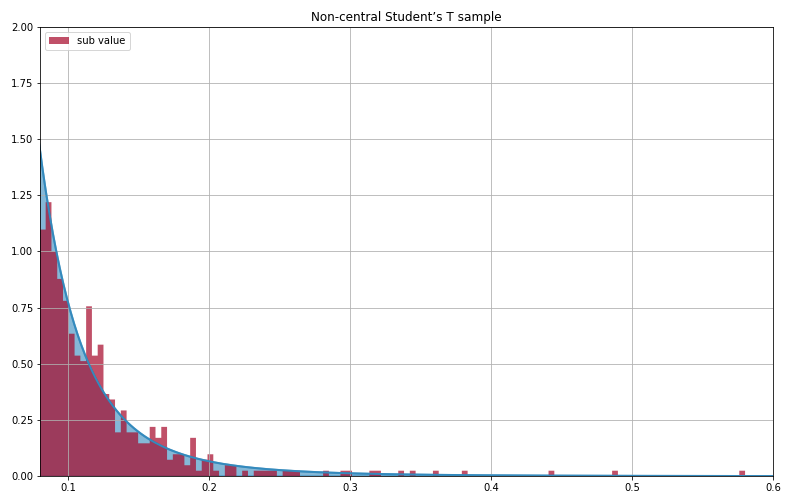
上図のように、0.3以降の値を過小評価してしまっています。
前々回パラメータを推測した正規分布では、-0.65以下の値をとる下側累積確率が1.57e-32、前回のコーシー分布では-0.65以下の値をとる下側累積確率が1.22e-02、そして今回の非心t分布では-0.65以下の値をとる下側累積確率が9.79e-05となっています。
この結果から、全体の当てはまり度は非心t分布、極端な値を考慮しているのはコーシー分布と言えそうです。 (訂正) 得られた分布から値動きを再現したところ、コーシー分布は論外な動きをしていました。詳しくは前回のページをご覧ください。
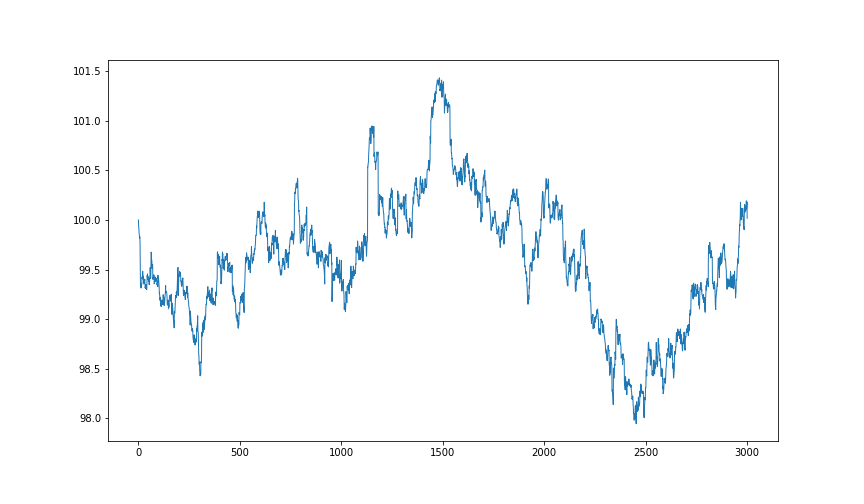
補足追加
得られた分布から値動きを再現
3000区間分生成
これはコーシー分布の時とは異なり妥当な変化をしています。
また、たまに起こる急騰、急落も何となく再現できているのではないでしょうか?
まとめ
今回は非心t分布と仮定してパラメータを推測しました。
非心t分布の良いところは、平均、分散が計算できる可能性があるので、コーシー分布よりも数学的に使いやすくなっています。
結果を無理やり数学的に解釈したら、何かしらの母集団から4.3個ずつ標本を取り出して
$$T = \frac{(\bar{X_n} - \mu)\sqrt{n}}{U_n}$$
($n$は標本数 $\bar{X_n}$は標本平均 $U^{2}_{n}$は不偏分散)
とした時のTの分布が為替の値動きということなのでしょうか?
この母集団は何なのか今の所見当がつきませんが・・・
もしかしたら、式に組み込めるかも・・・?
引き続き何か良い確率分布をご存知の方はコメントをお願いします。