はじめに
大学の図書館で「Pythonで体験するベイズ推論」を借りてベイジアンに染まったので、今回は本を読んだアウトプットとして為替の値動きが本当に正規分布に従っているのかPyMC2を使用してMCMC法でパラメータを推測してみたいと思います。
PyMC2の使い方は簡単に説明しますが、詳しい使い方や説明は是非本をお読み下さい。
確率分布あたりの詳しい説明も省かせていただきます。
また、ベイズ的な議論は初めてするので、間違い等があれば教えて下さい。
続きを書きました
為替の値動きはコーシー分布に従うのか?PyMC2を使って確かめる
実行環境
maxOS High Sierra
Anaconda Python3.5 の仮想環境
Jupyter Notebook
PyMC2
使用する為替データは、USD-JPYの15分足2003.09.01〜2017.11.17の終値で、最新から10000区間分を使います。
今回はPyMC2を用いてMCMC法でデータが従っているであろう確率分布のパラメータを推測していきます。
為替データを見る
まずは為替データを見てみましょう。
プログラム
import scipy.stats as stats
from IPython.core.pylabtools import figsize
import numpy as np
import matplotlib.pyplot as plt
import pymc as pm
import pandas as pd
%matplotlib inline
df = pd.read_csv('USDJPY_UTC_15Mins_Bid_2003.09.01_2017.11.17.csv', sep=',')
value = np.array(df.loc[:, "Close"])[::-1] #新しい順にNumpy arrayにする
print(df.head(3))
figsize(14, 13)
obs = 10000
colors = ["#348ABD", "#A60628", "#7A68A6", "#467821"] #plotの色
_previous_day = np.roll(value, -1) #差を求めるために1つずつずらす
sub_value = (value - _previous_day)[:obs] #10000区間の終値の差
plt.subplot(211)
plt.plot(sub_value[::-1]) #古い順で表示
plt.grid()
plt.subplot(212)
plt.hist(sub_value, bins=300, histtype="stepfilled",
density=True, color=colors[0], label="sub value")
plt.vlines(sub_value.mean(), 0, 13, "k", "--", linewidth=0.5)
plt.xlim(-0.67, 0.6)
plt.legend()
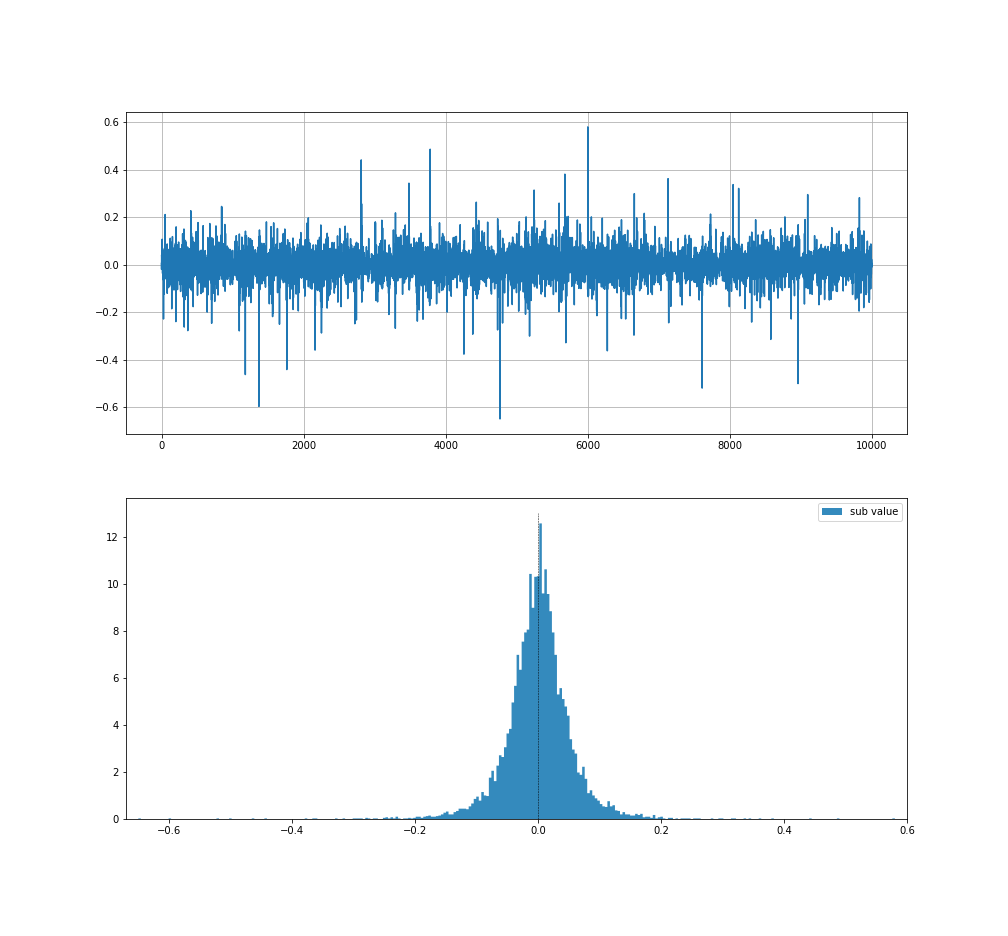
実行結果
| Time (UTC) | Open | High | Low | Close | Volume | |
|---|---|---|---|---|---|---|
| 0 | 2003.09.01 10:30:00 | 116.49 | 116.57 | 116.43 | 116.53 | 363.0 |
| 1 | 2003.09.01 10:45:00 | 116.52 | 116.55 | 116.36 | 116.43 | 411.0 |
| 2 | 2003.09.01 11:00:00 | 116.42 | 116.44 | 116.35 | 116.38 | 324.0 |
ヒストグラムを見ると確かに正規分布っぽい。
これがファイナンス分野で正規分布として仮定されている理由の一つみたいです。(1番の理由は正規分布が数学的にとても扱いやすいから)
ですが、本当に正規分布なのでしょうか?
例えば、グラフを見ると-0.65あたりの数値が出現してますが、正規分布と仮定しヒストグラムから多めに見積もって標準偏差を0.1としても、6σ以上の数値で下側累積確率が4.016e-11とかいうとんでもない数値叩き出してますよ!!!
ですが、株や為替ではこの辺の数値は珍しくありません。
この辺からすでに正規分布に従うのか怪しいですが、 早速MCMCで正規分布のパラメータを推測してみましょう。
PyMCで正規分布のパラメータを推測する
ということで、これらのデータが正規分布から得られたと仮定して平均と標準偏差を推測していきます。
まずMCMCを使用するために平均と標準偏差の事前分布を設定します。
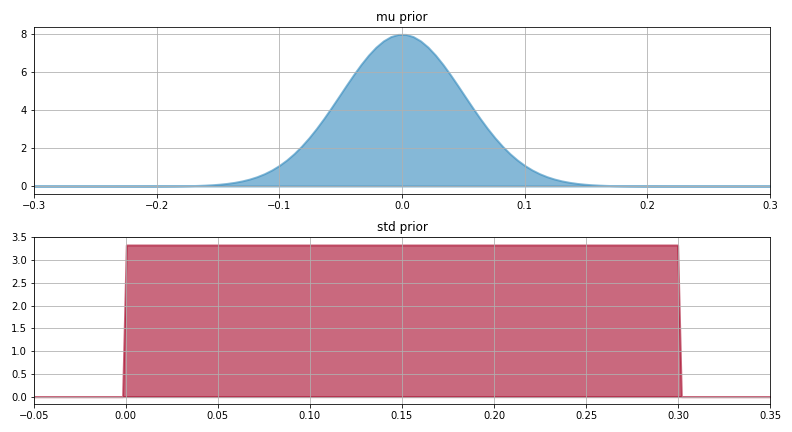
今回は、ヒストグラムを見て
平均(mu):平均0 標準偏差0.05の正規分布
標準偏差(std):0~0.3の一様分布
にしました。
PyMC2では、正規分布のパラメータとして、分散の逆数である精度(τ)を使用します。
事前分布の確認
figsize(11, 6)
# 正規分布で近似
mu = pm.Normal("mu", 0, 1./ 0.05**2) #平均の事前分布は正規分布
tau = 1. / pm.Uniform("std", 0, 0.3)**2 #標準偏差の事前分布は一様分布
# 結果のプロット
plt.subplot(211)
x = np.linspace(-0.3, 0.3, 100)
a_y = stats.norm.pdf(x, 0, scale=0.05)
plt.fill_between(x, 0, a_y, color=colors[0], linewidth=2,
edgecolor=colors[0], alpha=0.6)
plt.title("mu prior")
plt.xlim(-0.3, 0.3)
plt.tight_layout()
plt.grid()
plt.subplot(212)
x = np.linspace(-0.05, 0.35, 200)
b_y = stats.uniform.pdf(x, 0, 0.3)
plt.fill_between(x, 0, b_y, color=colors[1], linewidth=2,
edgecolor=colors[1], alpha=0.6)
plt.title("std prior")
plt.xlim(-0.05, 0.35)
plt.tight_layout()
plt.grid()
事前分布の実行結果
各種パラメータの事前分布を決めたら、データを保存してMCMCを実行します。
PyMCの実行
# データが正規分布から得られたとする
obs_1 = pm.Normal("obs_1", mu, tau, value=sub_value, observed=True)
# データと平均、精度をモデルにしてMCMCの実行
model_1 = pm.Model([obs_1, mu, tau])
mcmc_1 = pm.MCMC(model_1)
# 最後の30000回の内、さらに間引いたものをsampleとして使用
mcmc_1.sample(100000, 70000, 3)
figsize(11, 6)
# muとstdの事後分布を取り出す
mu_samples = mcmc_1.trace("mu")[:]
std_samples = mcmc_1.trace("std")[:]
# 事後分布のプロット
plt.subplot(211)
plt.hist(mu_samples, bins=30, alpha=0.8, histtype="stepfilled",
color=colors[0], density=True)
plt.title("mu samples")
plt.grid()
plt.tight_layout()
plt.subplot(212)
plt.hist(std_samples, bins=30, alpha=0.8, histtype="stepfilled",
color=colors[1], density=True)
plt.title("std samples")
plt.grid()
plt.tight_layout()
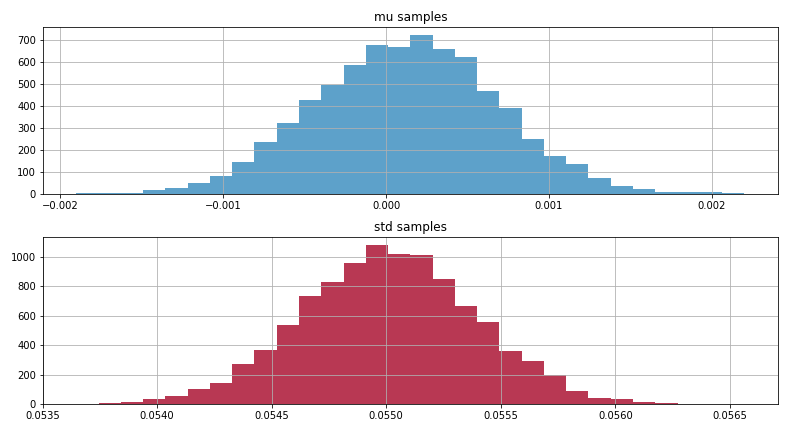
事後分布の結果
事後分布とは、事前分布と尤度の積で表されて、簡単に言うとデータが従っていそうな確率分布のパラメータの分布の事です。(ここがベイズ主義の分かりにくいところですが、ベイズ主義では母集団のパラメータは定まっていないことを思い出してください。母集団のパラメータも何かの確率分布に従っているのです。)
なので、平均と標準偏差の事後分布はこのようになりました。
収束して妥当そうな分布に落ち着いています。
続いて、得られた事後分布のパラメータを使用してscipyで正規分布を描き、データのヒストグラムと重ねてみましょう。ヒストグラムは面積が1になるように正規化してあります。
得られた事後分布から正規分布を描く
figsize(11, 7)
mu_mean = mu_samples.mean() #平均の事後分布の平均
std_mean = std_samples.mean() #標準偏差の事後分布の平均
print("mu_mean", mu_mean)
print("std_mean", std_mean)
# 重ね合わせ
x = np.linspace(-0.67, 0.6, 500)
a_y = stats.norm.pdf(x, mu_mean, scale=std_mean)
plt.fill_between(x, 0, a_y, color=colors[0], linewidth=2,
edgecolor=colors[0], alpha=0.6, label="norm dist\nmu:%.5f\nstd:%.5f" %(mu_mean, std_mean))
plt.hist(sub_value, bins=300, histtype="stepfilled", alpha=0.7,
density=True, color=colors[1], label="sub value") #densityは面積が1になるよう正規化
plt.title("normal sample")
plt.xlim(-0.67, 0.6)
plt.legend(loc="upper left")
plt.tight_layout()
plt.grid()
最終結果
mu_mean 0.00012458117978842259
std_mean 0.05501015709933814
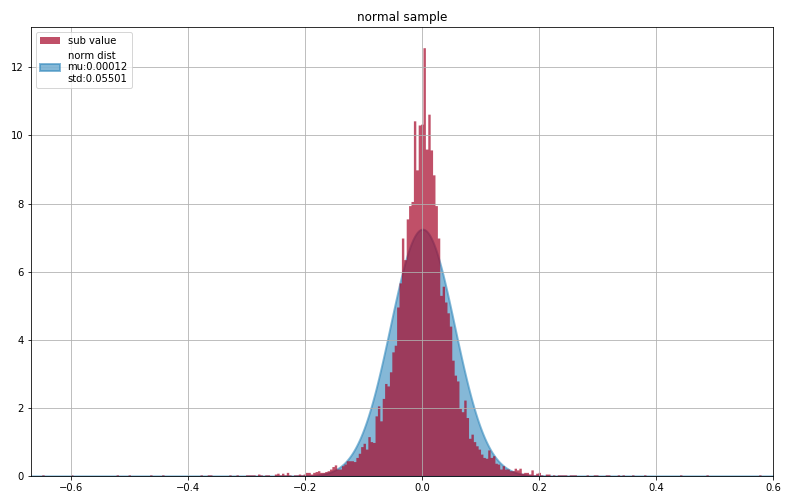
結果から言えること
まず一目見て気づくのは、平均の周辺は全く尖度が足りていません。
また、下図のように±0.15辺りからは正規分布で対応できていないです。
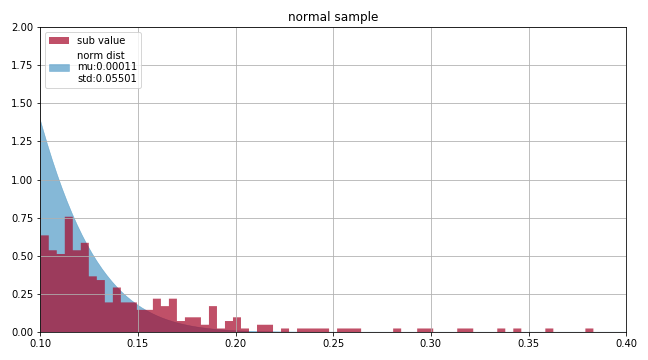
結果を見ると正規分布を仮定するのはやはり厳しいそうに見えます。特に問題なのは、やはり±0.15以降の出現率を極度に過小評価してしまっている点です。例えば、この正規分布では+0.30となる確率が2.5e-8です。正規分布と仮定してしまうと、この過小評価によって大損害を被る可能性があります。
補足追加
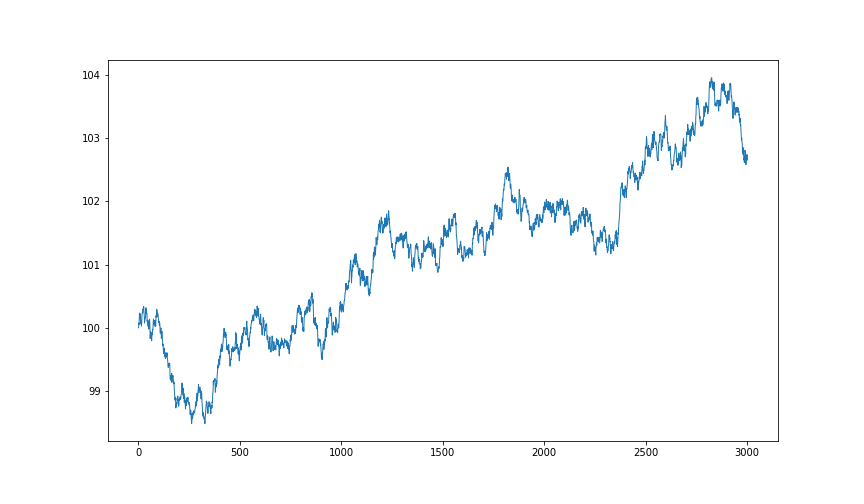
得られた分布から値動きを再現
3000区間分生成
良くある為替の動きに見えますね。
結果を受けて
では、為替の値動きは正規分布でないならどのような分布に基づいているのでしょうか?
調べてみると、為替や株の値動きはべき分布に従うと言われています。
なので次回はべき分布の一つであるコーシー分布と仮定してMCMCを行なっていきます。