はじめに
この記事は、前回の「為替の値動きは本当に正規分布に従うのか?PyMC2を使って確かめる」の続きです。
前回は、ファイナンスの世界で頻繁に仮定されている「為替の値動きは正規分布である」が本当なのかPyMC2を使用して確認してみました。
今回は、べき分布の一つであるコーシー分布と仮定して、MCMC法でパラメータを推測してみたいと思います。
非心t分布でもやってみました→ 為替の値動きは非心t分布に従うのか?PyMC2を使って確かめる
もし宜しければご覧ください。
実行環境
maxOS High Sierra
Anaconda Python3.5 の仮想環境
Jupyter Notebook
PyMC2
使用する為替データは、USD-JPYの15分足2003.09.01〜2017.11.17の終値で、最新から10000区間分を使います。
べき分布とは
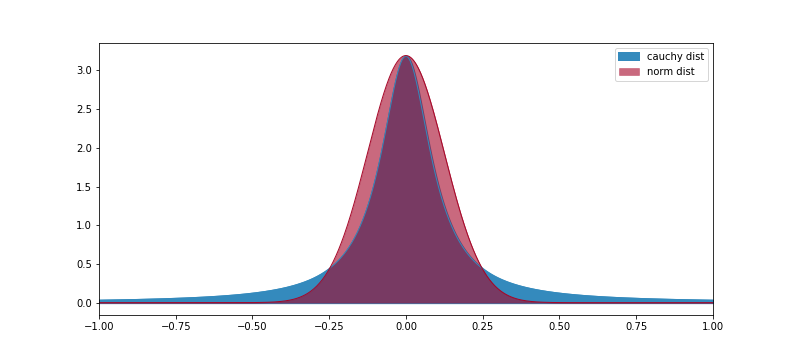
べき分布の特徴は長い裾野(ロングテール)です。極端な値をとることが起こりうる際に有効な分布とされています。下の図はべき分布の一つであるコーシー分布と正規分布のピークを揃えて重ねて描いてみたものです。
コーシー分布の方が尖度が高く、裾野が長いことが分かると思います。
またもう一つの特徴としてべき分布は平均と分散が意味を持たないか、そもそも定義ができません。
感覚的に言うと、極端な値をとる可能性が少なくないので平均が(-∞,∞)の任意の値を取り得るためです。(コーシー分布の場合)
今回はコーシー分布を使用します。コーシー分布の詳しい説明は、ウィキペディアをご覧ください。
為替データを見る
使用するものは前回と同じです。確認のためもう一度掲載します。
コードは前回と同じなので省略。
結果
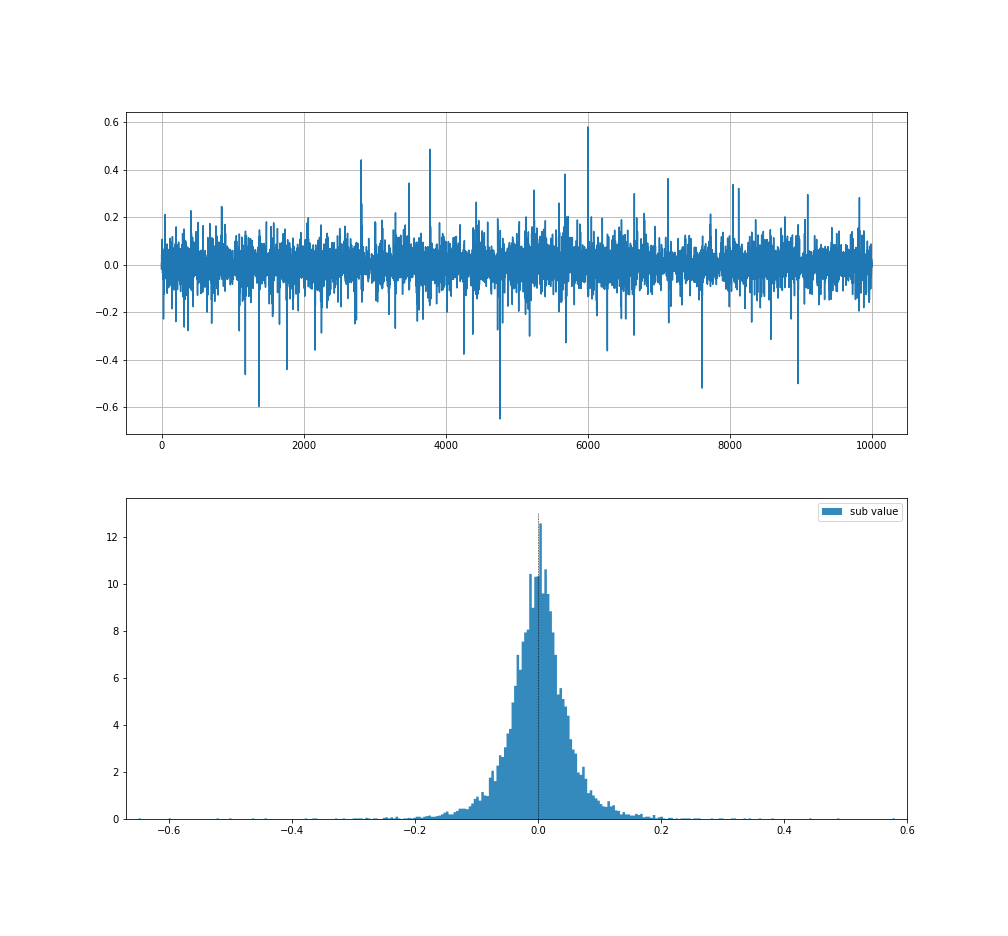
このヒストグラムについてコーシー分布と仮定してパラメータを推測していきます。
PyMC2でコーシー分布のパラメータを推測する
まずコーシー分布には、最頻値と半値半幅を与える尺度母数がパラメータとして必要です。
なので今回は、
最頻値(alpha):平均0 標準偏差0.05の正規分布
尺度母数(beta):0~0.3の一様分布
にしました。
これは、前回の平均と標準偏差と同じにしてあります。
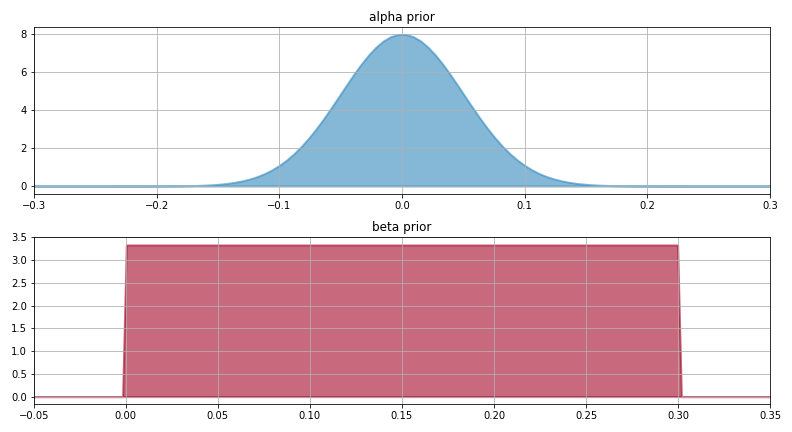
事前分布の確認
figsize(11, 6)
# コーシー分布で近似
alpha = pm.Normal("alpha", 0, 1./ 0.05**2) #最頻値の事前分布は正規分布 数値は上のヒストグラムから適当に
beta = pm.Uniform("beta", 0, 0.3) #半値半幅の事前分布は一様分布
plt.subplot(211)
x = np.linspace(-0.3, 0.3, 100)
a_y = stats.norm.pdf(x, 0, scale=0.05)
plt.fill_between(x, 0, a_y, color=colors[0], linewidth=2,
edgecolor=colors[0], alpha=0.6)
plt.title("alpha prior")
plt.xlim(-0.3, 0.3)
plt.tight_layout()
plt.grid()
plt.subplot(212)
x = np.linspace(-0.05, 0.35, 200)
b_y = stats.uniform.pdf(x, 0, 0.3)
plt.fill_between(x, 0, b_y, color=colors[1], linewidth=2,
edgecolor=colors[1], alpha=0.6)
plt.title("beta prior")
plt.xlim(-0.05, 0.35)
plt.tight_layout()
plt.grid()
結果
グラフは前回と同じです。
各種パラメータの事前分布を決めたら、データを保存してMCMCを実行します。
PyMC2の実行
# データがコーシー分布から得られたとする
obs_2 = pm.Cauchy("obs_2", alpha, beta, value=sub_value, observed=True)
model_2 = pm.Model([obs_2, alpha, beta])
mcmc_2 = pm.MCMC(model_2)
# 最後の30000回の内、さらに間引いたものをsampleとして使用
mcmc_2.sample(100000, 70000, 3)
figsize(11, 7)
# alphaとbetaの事後分布を取り出す
alpha_samples = mcmc_2.trace("alpha")[:]
beta_samples = mcmc_2.trace("beta")[:]
# 事後分布のヒストグラム
plt.subplot(211)
plt.hist(alpha_samples, bins=30, alpha=0.8, histtype="stepfilled",
color=colors[0], density=True)
plt.title("alpha samples")
plt.grid()
plt.tight_layout()
plt.subplot(212)
plt.hist(beta_samples, bins=30, alpha=0.8, histtype="stepfilled",
color=colors[1], density=True)
plt.title("beta samples")
plt.grid()
plt.tight_layout()
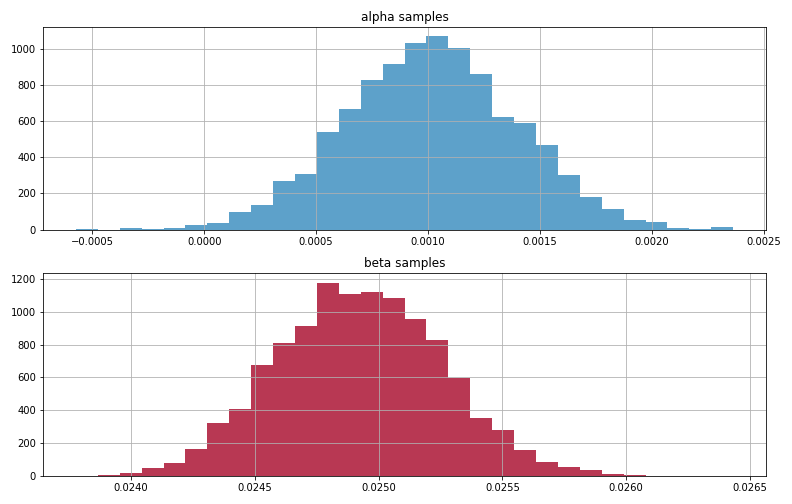
事後分布の結果
alphaとbetaの事後分布はこのようになりました。
収束して妥当そうな分布に落ち着いています。
続いて、得られた事後分布のパラメータを使用してscipyでコーシー分布を描き、データのヒストグラムと重ねてみましょう。ヒストグラムは面積が1になるように正規化してあります。
得られた事後分布からコーシー分布を描く
figsize(11, 7)
alpha_mean = alpha_samples.mean() #alphaの事後分布の平均
beta_mean = beta_samples.mean() #betaの事後分布の平均
print("alpha_mean", alpha_mean)
print("beta_mean", beta_mean)
# コーシー分布を描く
x = np.linspace(-0.67, 0.6, 500)
a_y = stats.cauchy.pdf(x, alpha_mean, scale=beta_mean)
plt.plot(x, a_y, lw=2, color=colors[0])
plt.fill_between(x, 0, a_y, color=colors[0], linewidth=2,
edgecolor=colors[0], alpha=0.6, label="caushy dist\nalpha:%.5f\nbeta:%.5f" %(alpha_mean, beta_mean))
plt.hist(sub_value, bins=300, histtype="stepfilled", alpha=0.7,
density=True, color=colors[1], label="sub value")
plt.title("caucy sample")
plt.xlim(-0.67, 0.6)
plt.legend(loc="upper left")
plt.tight_layout()
plt.grid()
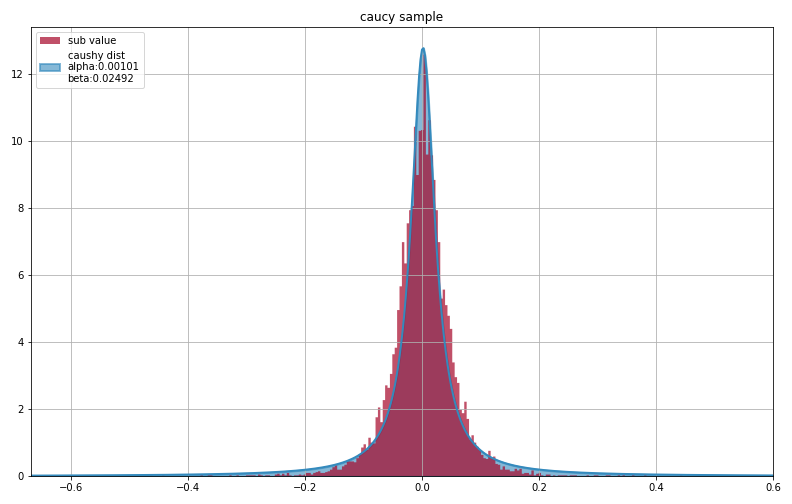
最終結果
alpha_mean 0.0010141381117027678
beta_mean 0.02492383074426156
前回の正規分布よりも上手く分布を表現できているのではないでしょうか?
結果から言えること
正規分布の時に比べ、尖度は上手く改善されています。
ただ逆に、正規分布の時に比べて±(0.05~0.1)あたりが少し気になります。
また、下図のように正規分布では表現できなかった極端な値のところを見てみても上手く表現できているように見えます。
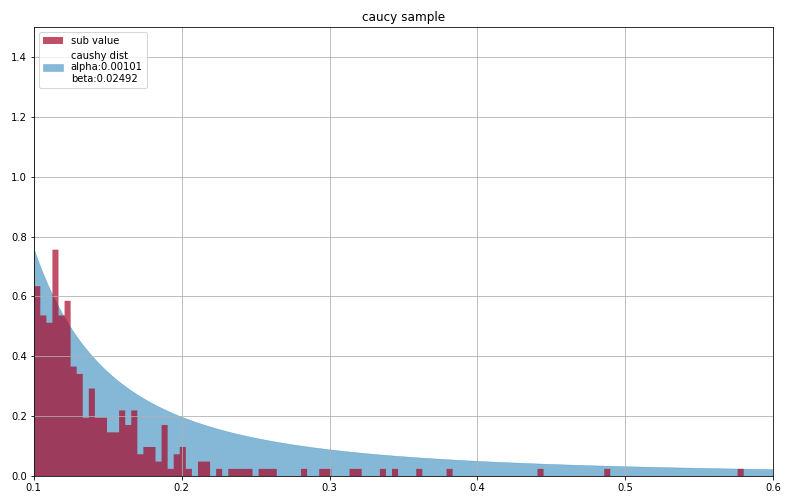
ちなみに前回パラメータを推測した正規分布では、-0.65以下の値をとる下側累積確率が1.57e-32というプランク定数並みの数値でしたが、今回のコーシー分布では-0.65以下の値をとる下側累積確率が1.22e-2という現実味を帯びた値になってます。これがコーシー分布を仮定した利点です。
補足追加
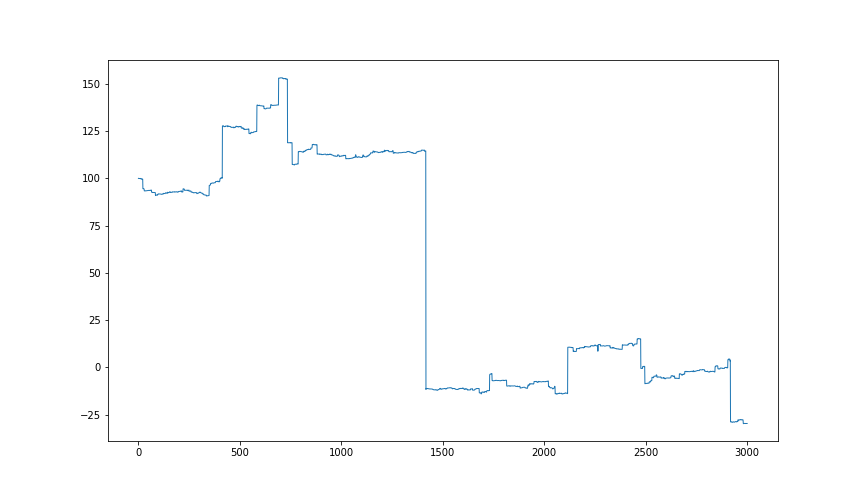
得られた分布から値動きを再現
・・・・・・論外ですね。。。
裾野が広いことが仇となり、極端な値を連発しすぎています。
これは使えなそうですね。
まとめ
確かに正規分布よりもコーシー分布の方がうまく表現できそうなことが分かりました。
しかし、為替の値動きにコーシー分布を仮定しても平均も分散もない為、為替の値動きについて何かしらの数学的な議論をするにはまだまだ勉強が必要そうです。
不労所得への道はまだまだ遠いですね・・・
何か他に良い確率分布をご存知の方はコメントをお願いします。