論文紹介・画像引用
Google Brainより2019.3.6提出
https://arxiv.org/pdf/1903.02271v1.pdf
本研究のGANの特徴と成果
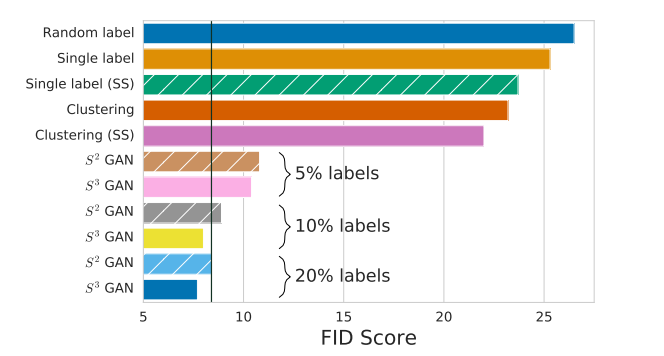
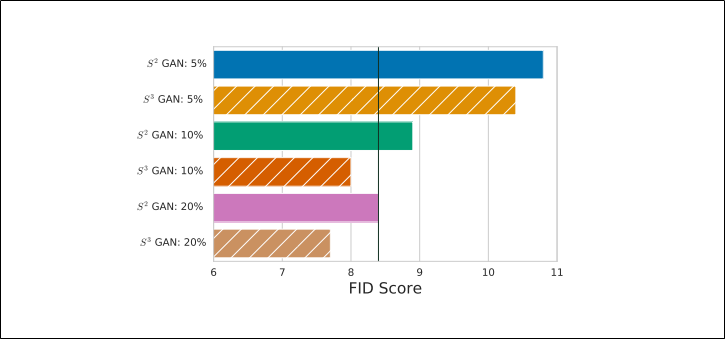
FIDスコア(低い方が良い)
スコア8~9の間にある縦線はベースライン(すべてラベル付けされた画像を使ったBigGAN)
本研究の方法($S^3GAN$)では
ラベル付けされた画像は全体のたった10%にも関わらずSOTAであるBigGANと同等の性能になった
また全体の20%をラベル付けされた画像にするとBigGANを超える性能となった

解像度128×128
上段:BigGAN
下段:画像の10%のみラベルありのデータを使った$S^3GAN$
データの現実とその対策
これまでの鮮明な画像生成は大量のラベル付きデータによって実現してきた
しかし現実的には、ほとんどのデータはラベル付けされていない・ラベル付け自体が多大なコスト・間違ったラベルが発生しやすいといった問題がある
ラベル付きデータが少ない状況では?
Discriminatorに与える本物画像のラベルをこれまでのようにあらかじめ用意できない場合は、
推測したラベルを使う
推測ラベルを得るためにself-supervised(後述)とsemi-supervised(後述)を利用する
これまでのGANにおけるラベル情報の使い方
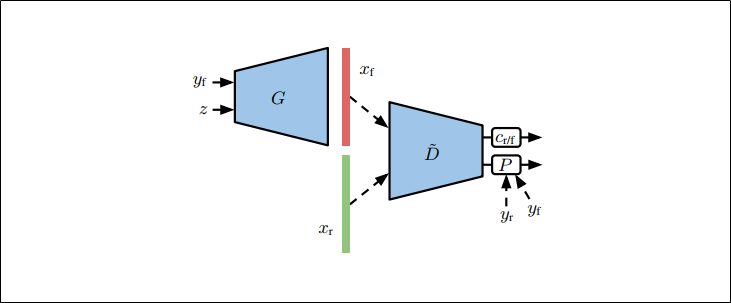
projection discriminatorを使ったconditinal GAN
BigGANは上図と同様の形式
入力が本物画像$x_r$(ラベル:$y_r$)なのか生成画像$x_f$(ラベル:$y_f$)を予測する
$\tilde{D}$(discriminatorの分類器にかける前まで、特徴表現を得る部分)を利用して、以下2つの判別をする
①条件なしの分類器:$c_{r/f}$
単純にdiscriminatorに来た画像が本物画像か生成画像かを判別する
②projection層$P$を利用したクラス条件ありの分類器
discriminatorに来た画像がクラス情報に合致した本物画像なのかを判別する
①と②をまとめると下記の式になる
$D(x,y)=c_{r/f}(\tilde{D}(x))+P(\tilde{D}(x),y)$
事前学習する方法
GANの学習に入る前に下記のような事前学習をするステップを踏む方法
特徴抽出器$F$の学習をする→ラベルを推測する→GANの学習に入る
1,クラスタリングによるラベリング
①本物の訓練画像の特徴表現を学習する
下記の$self-supervision loss$を小さくすることで特徴抽出器$F$を学習させる
$$L_{R}=-\frac{1}{|R|}\sum_{r\in{R}}E_{x\sim{p_{data}(x)}}[\log{p(c_R(F(x^{r}))=r})]$$
$R$:4つの回転角度{0°,90°,180°,270°}
$x^r$:角度$r$で回転させた画像$x$
$c_R$:角度$r$(画像が何度回転しているか)を予測する分類器
上記の式を言葉で表すなら、
回転させた画像から抽出された特徴を基に何度回転した画像なのかを正しく判定できるか
$F$が上手く特徴抽出できていれば何度回転したものかを正しく判定できるはず
②特徴表現をクラスタリングする
特徴抽出器$F$の学習が完了したら、訓練画像の特徴表現に対してクラスタリング$c_{CL}$をする
③クラスタの割り当てをラベルとして使う
本物画像のラベルを$\hat{y}_{CL}=c_{CL}(F(x))$として推測しconditinal GANの学習する
④GenratorとDiscriminatorのlossを小さくする
$$L_{D}=-E_{x\sim{p_{data}(x)}}[\min(0,-1+D(x,c_{CL}(F(x))))] -E_{(z,y)\sim{\hat{p}(z,y)}}[\min(0,-1-D(G(z,y),y))]$$
$$L_{G}=-E_{(z,y)\sim{\hat{p}(z,y)}}[D(G(z,y),y)]$$
$\hat{p}(z,y)=p(z)\hat{p}(y)$
$p(z)$:$N(0,I)$
$\hat{p}(y)$:クラスタラベル$c_{CL}(F(x))$の分布
2,半教師あり学習を利用したラベリング
訓練画像の一部についてのラベルは得られたという状況を想定
この章での方法を$S^{2}GAN$とする
①特徴表現を学習する・少量のラベルを使って正しく分類する
self-supervisionによって特徴表現を得られるように$F$を訓練すると同時に、
与えられたラベルを利用してその特徴表現を正しく分類できるように分類器を訓練する
これは以下の式を小さくすることと同じ意味である
$$L_{S^{2}L}=-\frac{1}{|R|}\sum_{r\in{R}}E_{x\sim{p_{data}(x)}}[\log{p(c_R(F(x^{r}))=r})]+γE_{(x,y)\sim{p_{data}(x,y)}}[\log{p(c_{S^{2}L}(F(x^{r}))=y)}]$$
$c_{R}$:回転角度$r$を予測する分類器
$c_{S^{2}L}$:ラベル$y$を予測する分類器
$γ>0$として損失項のバランスをとる
第1項はself-supervisionの損失項なので「クラスタリングによるラベリング」の章で見た式と全く同じ形
第2項は半教師あり学習の損失項
②GenratorとDiscriminatorのlossを小さくする
$F$と$c_{s^{2}L}$の学習が終わったら、GANの学習に進む
本物画像のラベルは$\hat{y}_{S^{2}L}=c_{S^{2}L}(F(x))$とする
$$L_{D}=-E_{x\sim{p_{data}(x)}}[\min(0,-1+D(x,c_{S^{2}L}(F(x))))] -E_{(z,y)\sim{p(z,y)}}[\min(0,-1-D(G(z,y),y))]$$
$$L_{G}=-E_{(z,y)\sim{p(z,y)}}[D(G(z,y),y)]$$
$p(z,y)=p(z)p(y)$
$p(z)$:$N(0,I)$
$p(y)$:一様カテゴリ分布
同時学習する方法
事前学習する方法で示したものは
特徴抽出器$F$の学習→ラベルの推測という2ステップを踏まないとGANの学習に入れなかった
それに対して、同時学習ではGANの学習をしながらラベルを推測するという方法をとる
1,教師なしによるラベリング
Single Label
以下の2点を行い、ラベルを完全に取り除く方法
・すべての本物画像と生成画像に同じラベルを与える
・discriminatorからprojection層を取り除く
→$D(x)=c_{t/f}(\tilde{D}(x))$
Random Label
ラベルのない本物画像にランダムなラベルを割り当てる方法
→generatorにとって有益
generatorへのメリット
・$z$とは異なる乱数性の追加
・class-conditional BatchNormの埋め込み行列へのパラメーター追加
・これまでのようにあらかじめラベルがついていると、そのラベル情報がヒントとなってdiscriminatorが判別しやすくなっていたが、ランダムなラベルだとそういったことが起きない
・しかし、後述の実験結果ではRandom Labelの性能はSingle Labelよりも悪いため、Random Labelの良さはよくわからない
2,半教師あり学習を利用したラベリング
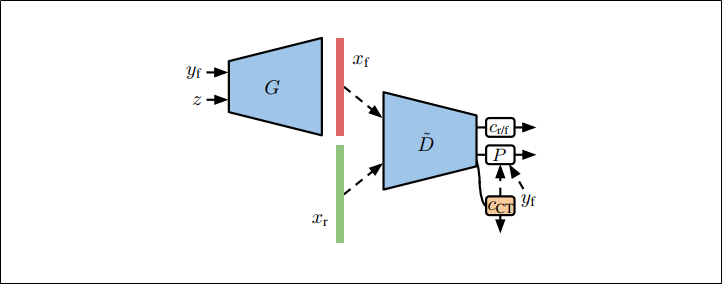
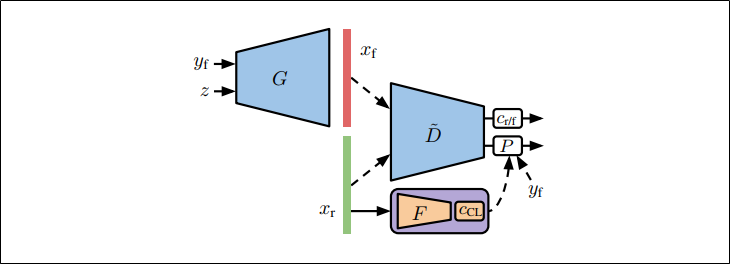
$S^{2}GAN-CO$
GANの学習をしながら特徴表現$\tilde{D}$を入力として補助分類器$c_{CT}$を学習する
一部のラベルありデータを参考にして、ラベルの付いていない本物データのラベルを予測する
こうすることでこれまでのような特徴抽出器$F$や分類器$c_{S^{2}L}$の訓練をGANの訓練の前にするといった作業がなくなる
Discriminatorの損失関数
4つの項で構成されている
それぞれの項の数式とその意味についてみていく
$$L_{D}=L_{D_{1}}+L_{D_{2}}+L_{D_{3}}+L_{D_{4}}$$
第1項
$$L_{D_{1}}=-E_{(x,y)\sim{p_{data}(x,y)}}[\min(0,-1+D(x,y))]$$
ラベルの付いた本物画像(全体の中の一部のデータ)についてdiscriminatorが正しく判別できるか
第2項
$$L_{D_{2}}=-λE_{(x,y)\sim{p_{data}(x,y)}}[\log{p(c_{CT}(\tilde{D}(x))=y)}]$$
$λ>0$とする
ラベルの付いた本物画像を補助分類器$c_{CT}$が正しく分類できるか
第3項
$$L_{D_{3}}=-E_{x\sim{p_{data}(x)}}[\min(0,-1+D(x,c_{CT}(\tilde{D}(x))))]$$
元々ラベルが用意されていなかった本物画像(ラベルは$c_{CT}$によって予測されたものを使う)をdiscriminatorが正しく判別できるか
$c_{CT}$が優れていて適切なラベルを付けることができれば、discriminatorは正しく本物と判別できるため損失は小さくなる
第4項
$$L_{D_{4}}=-E_{(z,y)\sim{p(z,y)}}[\min(0,-1-D(G(z,y),y))]$$
ラベルの付いた生成画像をdiscriminatorは正しく判別できるか
GANの学習をしながらself-supervision
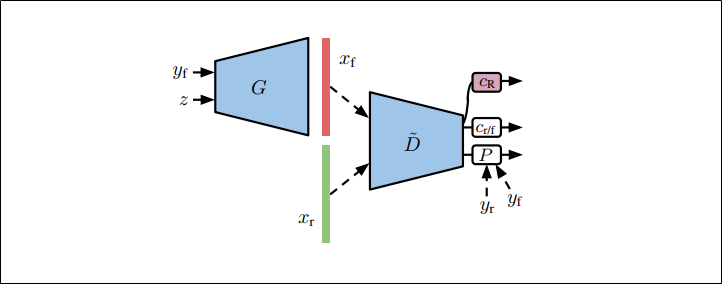
GANの学習と同時に、角度予測によるself-supervisionをする
discriminatorは入力画像が本物か偽物かを予測するだけでなく、補助分類器$c_{R}$によって画像が何度回転しているかについても予測する
この方法は以前の研究でGANの学習を安定化させるはたらきがあることがわかっている
そのため、これまでに提案した事前学習する方法と同時学習する方法に、この方法を加えることで効果がある
すなわち、以下の損失項をdiscriminatorとgeneratorにそれぞれ加えることになる
・discriminatorに加える項
$$-\frac{\beta}{|R|}\sum_{r\in{R}}E_{x\sim{p_{data}(x)}}[\log{p(c_R(\tilde{D}(x^{r}))=r})]$$
・generatorに加える項
$$-\frac{\alpha}{|R|}E_{(z,y)\sim{p(z,y)}}[\log{p(c_R(\tilde{D}(G(z,y)^{r})=r})]$$
$\alpha,\beta>0$で損失項のバランスをとる
様々な提案手法の性能を比較
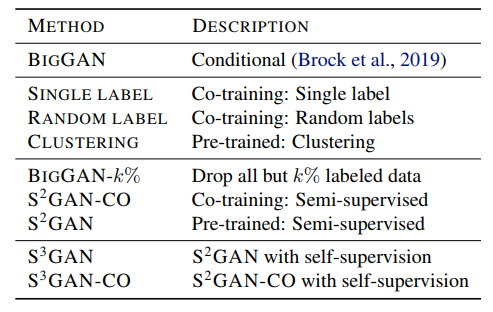
Pre-trained: 「事前学習する方法」の章で提案したもの
Co-training: 「同時学習する方法」の章で提案したもの
with self-supervision: 「GANの学習をしながらself-supervision」の章で提案したもの
すべてのデータにラベルのある状況で生成された**BigGAN(FID:8.4, IS:75.0)**と同等もしくはそれ以上の質の画像を、本研究で提案したラベルがないもしくはわずかにあるという方法で生成できるのかがポイント
教師なしの方法
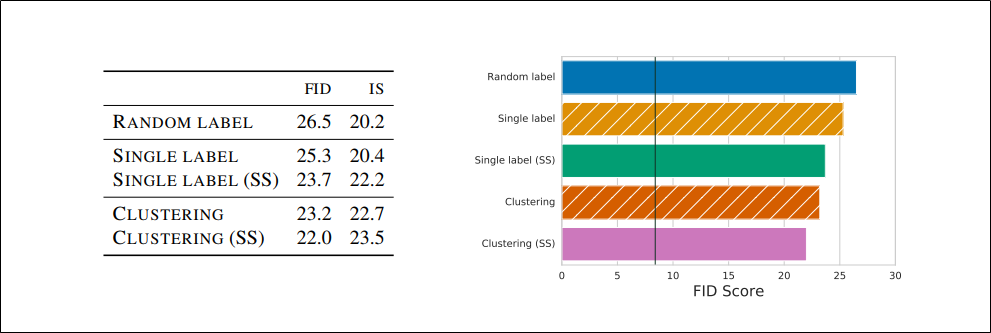
・教師なしであるSingle LabelとRandom LabelではどちらもFIDが25、ISが20ぐらいのためBigGANと同じ性能にするには他の方法を使ってラベルを追加する必要がある
・事前学習により特徴表現を得て、それをクラスタリングするという方法(表ではClustering)を使うとどちらの指標も10%ほど良くなっている
・クラスタリングを利用する方法はBigGANと比べれば良くないが、教師なしの生成に関して言えばSOTAである(これまでの教師なし生成のベストFIDは33、データはImagenet)
・上表の(SS)は「GANの学習をしながらself-supervision」の章で提案したものを追加した場合を表す
どんな方法に追加しても性能を向上させていることがわかる
半教師ありの方法
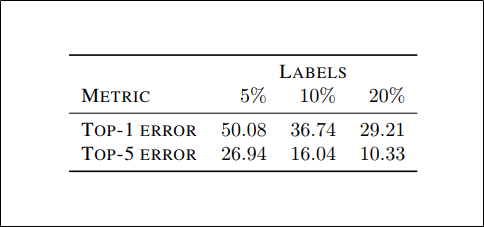
ラベル予測のエラー率
事前学習でself-supervisedとsemi-supervisedを利用した$c_{S^{2}L}(F(x))$がImagenetの検証データでラベル予測をしたときのエラー率
下表(エラー率ではなく性能比較の表)を見るとラベルを20%使った$S^2GAN$はFID・ISともにBigGAN(FID:8.4, IS:75.0)と同等の性能を示しているため、Imagenetの分類タスクそのもので考えると物足りない精度だがBigGAN以上の画像生成をするということに関しては十分なラベルの質であると言うことができる
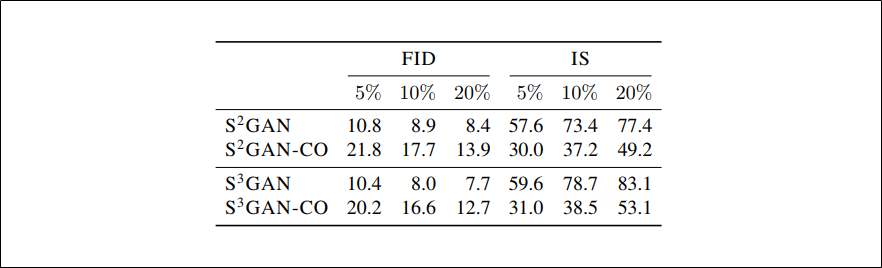
性能比較
$S^2GAN-CO$:同時学習の方法
$S^3GAN$:事前学習の方法に「GANの学習をしながらself-supervision」の章で提案したものを追加した方法
$S^3GAN-CO$:同時学習の方法に「GANの学習をしながらself-supervision」の章で提案したものを追加した方法
・同時学習よりも事前学習の方が良い性能である
・「GANの学習をしながらself-supervision」の章で提案したものはどちらの方法に追加しても性能向上に貢献している
・$S^2GAN-CO$は同時学習だが、$S^2GAN$と比べて学習が安定していないというわけではない
・$BigGAN-k%$は非常に不安定で60k~120kイテレーションで崩壊した
GANの学習をしながらself-supervisionの方法を追加をする効果
・self-supervisionを追加することでどのような方法でもFIDは減少し、ISは増加するという結果になる
・10%のラベルでBigGANと同等の性能になり、20%のラベルを使うとBigGANを上回る性能(FIDとIS両方)になる
ハードラベルとソフトラベル
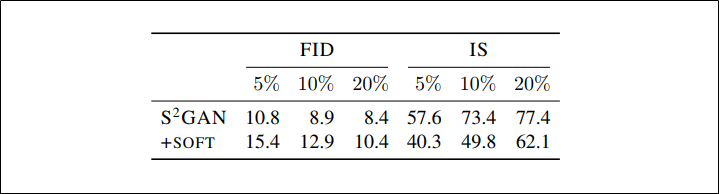
・ソフトラベルよりもハードラベルの方が良いことが上表からわかる
高解像度を生成する

$S^3GAN$(ラベル10% 256×256) 潜在空間でinterpolation

$S^3GAN$(ラベル10% 256×256) 1つのクラスから多様な画像が生成できている
ラベルデータを5%以下にする
$S^3GAN$をラベル2.5%で実験してみるとFIDが13.6、ISが46.3となった
この結果より、少しでもラベルを使うことで教師なし生成の性能(FID:33)を大きく上回る結果になることがわかる
まとめ
・self-supervisedとsemi-supervisedを利用することでラベルありデータが少ない状況でも自然な画像生成ができる
self-supervised: ラベルのないデータから特徴表現を取得し、それに基づいてラベルを推測する
semi-supervised: 半教師あり学習、限られたラベルありデータを参考にしてラベルなしデータのラベルを推測する
・ラベル予測のための手段として事前学習と同時学習があり、性能としては事前学習の方が良いが同時学習の場合はGANの学習の前に2ステップ(①特徴抽出器の学習、②ラベル推測のための分類器の学習もしくはクラスタリング)を踏まなくてすむという利点がある
・ラベルあり画像10%→SOTAであるBigGANと同等の性能
・ラベルあり画像20%→BigGANを超える性能